Complete Solutions to 1.10 प्रत्यास्थता of chapter सामान्य भौतिकी of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | सामान्य भौतिकी |
| BHARTI_BHAWAN | 1.10 प्रत्यास्थता |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
दो पदार्थो A और B के लिए प्रतिबल - विकृति (stress-strain) ग्राफ चित्र 1.10-1 में दर्शाए गए है। इन ग्राफो को एक ही पैमाना (scale) मानकर खींचा गया है।
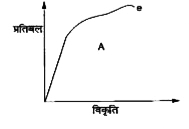
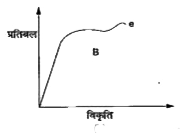
किस पदार्थ का यंग प्रत्यास्थता गुणांक अधिक है ?04:50View Solutionदो पदार्थो A और B के लिए प्रतिबल - विकृति (stress-strain) ग्राफ चित्र 1.10-1 में दर्शाए गए है। इन ग्राफो को एक ही पैमाना (scale) मानकर खींचा गया है।


दोनों पदार्थो में कौन अधिक मजबूत है ?04:17View Solutionनिम्नलिखित दोनों कथनो को ध्यान से पढ़े और करणसहित बताएँ कि वे सत्य (true) है या असत्य (false)?
इस्पात (steel) की अपेक्षा रबर (rubber) का यंग गुणांक अधिक है।02:51View Solutionनिम्नलिखित दोनों कथनो को ध्यान से पढ़े और करणसहित बताएँ कि वे सत्य (true) है या असत्य (false)?
किसी कुंडली (coil) का तन्न (stretching) उसके अपरूपण गुणांक से निर्धारित होता है।01:34View Solution1.5 m त्रिज्या का इस्पात (steel) का एक केवल (cable) भार उठाने के लिए इस्तेमाल किया जाता है। यदि इस्पात के लिए अधिकतम उचित प्रतिबल (permissible stress) `4 xx 10^(8) N m^(-2)` है, तो उस अधिकतम भार की गणना कीजिए जिसे केवल उठा सकता है।
02:31View Solutionधातु की दो पट्टियों (strips) के सिरों को चार रिवेट (rivet) से आपस में जोड़ दिया जाता गया है। प्रत्येक रिवेट का व्यास 6 m m है। यदि रिवेट पर अपरूपण प्रतिबल (shearing stress) `6 . 9 xx 10^(7)` Pa से अधिक नहीं बढ़ता हो, तो रिवेट की हुई पट्टी द्वारा आरोपित तनाव का अधिकतम मान कितना होगा ? मान ले कि प्रत्येक रिवेट - चौथाई भार वहन करता है।
04:10View Solutionनिम्नांकित चित्र 1.10-2 में किसी दिए गए पदार्थ के लिए प्रतिबल - विकृति वक्र दर्शाया गया है इस पदार्थ के लिए,
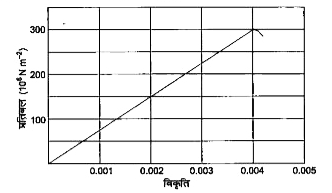
यंग प्रत्यास्थता गुणांक तथा02:59View Solutionनिम्नांकित चित्र 1.10-2 में किसी दिए गए पदार्थ के लिए प्रतिबल - विकृति वक्र दर्शाया गया है इस पदार्थ के लिए,

सन्निकट पराभव (yield strength) क्या है ?02:34View Solution6.3 m लंबे एवं `3 . 5 xx 10^(5) m^(2)` अनुप्रस्थ काट के स्टील के तार तथा 3.5 m लंबे एवं `5 xx 10^(-5) m^(2)` अनुप्रस्थ काट के ताँबे के तार पर दिए गए समान परिमाण के भारो को लटकाने पर उनकी लंबाइयो में समान वृद्धि होती है। स्टील तथा ताँबे के यंग प्रत्यास्थता गुणांकों में क्या अनुपात है ?
View Solution15 kg द्रव्यमान की एक ढंढ़ पट्टी को तीन तारो , जिनमे प्रत्येक की लंबाई 2m है, से सममितीय (symmetricaly) लटकाया गया है सिरों के दोनों तार ताँबे (Cu) के है तथा बीचवाला लोहे (Fe) का है तारो की व्यासो के अनुपात निकालिए , यदि प्रत्येक पर तनाव समान हो। `(Y_(Fe) = 1.91 xx 10^(11) Pa, Y_(Cu) = 1.10 xx 10^(11) Pa)`
07:38View Solutionनरम (soft) इस्पात के चार समरूप खोखले बेलनाकार संतभ 52,800 kg द्रव्यमान के किसी बड़े ढाँचे (structure) को आधार दिए हुए है। प्रत्येक स्तंभ की भीतरी तथा भरी त्रिज्याएँ क्रमशः 60cm तथा 80 cm है। भार वितरण को एकसमान मानते हुए प्रत्येक स्तभ की संपीडन विकृति की गणना कीजिए । (इस्पात के लिए `Y = 2 xx 10^(11) N m^(-2)` और `g = 10 m s^(-2)`)
04:39View Solution2.5 m m व्यास के दो तार, जिनमे एक इस्पात का तथा दूसरा पीतल का है, चित्र 1.10 - 3 के अनुसार भारित (loaded) है। बिना भार लटकाए (unloaded) इस्पात तथा पीतल के तारो की लंबाइयाँ क्रमशः 2.5 m तथा 1.5 m है यदि इस्पात तथा पीतल के यंग गुणांक क्रमशः `2 xx 10^(11) ` Pa तथा `0.91 xx 10^(11) ` Pa हो, तो इस्पात तथा पीतल के तारो में प्रसार की गणना कीजिए।
09:42View Solutionताँबे के एक ठोस घन (solid cube) की एक भुजा 10 cm की है। इस पर `7 xx 10^(6)` Pa का जलीय दाव लगाने पर इसके आयतन में संकुचन (contraction) निकालिए (ताँबे का आयतन प्रत्यास्थता गुणांक `K = 1.4 xx 10^(11) ` Pa )
04:07View Solutionएक लीटर जल पर दाब में कितना अंतर किया जाए कि वह `0.15%` से संपीडित (compressed) हो जाए ? [जल का आयतन प्रत्यास्थता गुणांक `K = 2 . 2 xx 10^(9) Pa` ]
02:44View Solutionकाँच के स्लैब (slab) पर 10 atm का जलीय दाब लगाने पर उसके आयतन में भिन्नात्मक अंतर (fractional change) की गणना कीजिए। (काँच का आयतन प्रत्यास्थता गुणांक `K = 3.7 xx 10^(10)Pa` )
View Solutionदिय गए आँकड़ो से जल के आयतन प्रत्यास्थता गुणांक की गणना कीजिए - प्रारभिक आयतन = 100 L, दाब में वृद्धि = 100 atm `(1 atm = 1.013 xx 10^(5) Pa)` अंतिम आयतन = 99.5 L नियत ताप पर जल तथा वायु के आयतन प्रत्यास्थता गुणांकों की तुलना कीजिए। सरल शब्दों में समझाइए कि यह अनुपात इतना अधिक क्यों है ?
06:32View Solutionकिसी स्थान पर प्रशांत महासागर की गहराई लगभग 11 km है। यदि `0.48 m^(3)` आयतन आयतन के इस्पात के गोले को उस स्थान पर जल से गिराया जाता है , तो महासागर के ताल पर पहुँचने पर गोले के आयतन में क्या परिवर्तन होगा ? उस स्थान पर महासागर के ताल पर जल का दाब `1.2 xx 10^(5)` Pa है और इस्पात का आयतन प्रत्यास्थता गुणांक 160 GPaहै।
02:36View Solutionताँबे का एक टुकड़ा , जिसका अनुप्रस्थ परिच्छेद `15 cm xx 18 cm` का `5 . 4 xx 10^(6)` N है , बल के तनाव से खींचा जाता है , जिससे केवल प्रत्यास्थ विरूपण (elastic shear) उत्पन्न हो,। उत्पन्न विकृति की गणना कीजिए। [ताँबे के लिए `eta = 4 . 2 xx 10^(10)` Pa]
03:30View Solutionऐलुमिनियम के किसी घन के किनारे लंबे है। इसका एक फलक (face) किसी ऊर्ध्वाधर दीवार (vertical wall ) से कसकर जुड़ा हुआ है। इस घन के सम्मुख फलक (opposite face) से 75 kg का एक द्रव्यमान जोड़ दिया गया है। ऐलुमिनियम का अपरूपण गुणांक (shear modulus)24 GPa है। इस फलक का ऊर्ध्वाधर विस्थापन (vertical deflection) कितना होगा ? `(g = 10 m s^(-2) , 1 Pa = N m^(-2))`
03:47View Solution5 cm भुजवाले ऐलुमिनियम के घन (cube) के पेंदी (bottom) के फलक (face) को किसी क्षैतिज दृढ़ आधार (base) से कसकर ऊपरी फलक पर स्पर्शीय (tangential) बल लगाया जाता है (चित्र 1.10-4)। यदि यह फलक 0.15 m m से अपरूपित होता है, तो निम्नलिखित की गणना करे।
अपरूपण विकृति03:22View Solution5 cm भुजवाले ऐलुमिनियम के घन (cube) के पेंदी (bottom) के फलक (face) को किसी क्षैतिज दृढ़ आधार (base) से कसकर ऊपरी फलक पर स्पर्शीय (tangential) बल लगाया जाता है (चित्र 1.10-4)। यदि यह फलक 0.15 m m से अपरूपित होता है, तो निम्नलिखित की गणना करे। `(eta = 2 . 5 xx 10^(10) N m^(-2))`
अपरूपण प्रतिबल03:49View Solution5 cm भुजवाले ऐलुमिनियम के घन (cube) के पेंदी (bottom) के फलक (face) को किसी क्षैतिज दृढ़ आधार (base) से कसकर ऊपरी फलक पर स्पर्शीय (tangential) बल लगाया जाता है (चित्र 1.10-4)। यदि यह फलक 0.15 m m से अपरूपित होता है, तो निम्नलिखित की गणना करे।
अपरूपण बल `(eta = 2 . 5 xx 10^(10) N m^(-2))`03:22View Solutionएक मीटर अतानित (unstretched) लंबाई के इस्पात के तार के एक सिरे से 4 kg का द्रव्यमान बाँधकर उसे एक ऊर्ध्वाधर वृत्त (vertical circle) में घुमाया जाता है (चित्र1.10-5 ) , वृत्त के निम्नतम बिंदु पर उसका कोणीय वेग 120 rpm है। तार के अनुप्रस्थ परिच्छेद का क्षेत्रफल `5.6 (m m )^(2)` है। तार में विस्तार की गणना कीजिए जब द्रव्यमान अपने पथ के निम्नतम बिंदु (lowest point) पर है (`g = 10 m s^(-2)` और इस्पात के लिए `Y = 2 xx 10^(11) N m^(-2)`)
04:05View Solution1.05 m लंबाई तथा नगण्य द्रव्यमान की एक छड़ XY को बराबर लबाई के दो तारो एक इस्पात का (तार A) तथा दूसरा ऐलुमिनियम का तार (तार B) द्वारा सिरों से लटका दिया गया है, जैसा कि चित्र 1.10 - 6 में दिखाया गया है A तथा B के तारो के अनुप्रस्थ परिच्छेद का क्षेत्रफल क्रमशः `1 m m ^(2)` और `2 m m ^(2)` है। छड़ के किस बिंदु P से एक द्रव्यमान m को लटका दिया जाए ताकि इस्पात तथा ऐलुमिनियम के तारो में

समान प्रतिबल तथा07:09View Solution1.05 m लंबाई तथा नगण्य द्रव्यमान की एक छड़ XY को बराबर लबाई के दो तारो एक इस्पात का (तार A) तथा दूसरा ऐलुमिनियम का तार (तार B) द्वारा सिरों से लटका दिया गया है, जैसा कि चित्र 1.10 - 6 में दिखाया गया है A तथा B के तारो के अनुप्रस्थ परिच्छेद का क्षेत्रफल क्रमशः `1 m m ^(2)` और `2 m m ^(2)` है। छड़ के किस बिंदु P से एक द्रव्यमान m को लटका दिया जाए ताकि इस्पात तथा ऐलुमिनियम के तारो में
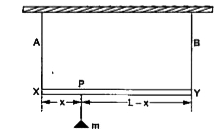
समान विकृति उत्पन्न हो। (इस्पात `Y = 2 xx 10^(11) N m^(-2)` के लिए ऐलुमिनियम के लिए `Y = 7 xx 10^(10) N m^(-1)`)07:09View Solutionनरम इस्पात के एक तार, जिसकी लंबाई 1 m तथा काट का क्षेत्रफल `0 . 50 xx 10^(2) cm^(2)` है, को दो खंभो के बीच क्षैतिज दिशा में प्रत्यास्थ सीमा (elastic limit) के अंदर तनित (stretch) किया जाता है। तार के मध्यबिंदु से 100 g का एक द्रव्यमान लटका किया जाता है। मध्यबिंदु पर अवनमन (depression) की गणना करे (इस्पात के लिए `Y = 2 xx 10^(11) N m^(-2)` और तार की लंबाई की तुलना में अवनमन को नगण्य माने)
16:05View Solutionजल का घनत्व उस गहराई पर, जहाँ दाब पृष्ठ की अपेक्षा अधिक हो, कितना होगा ? दिया गया है कि पृष्ठ पर जल का घनत्व `1.03 xx 10^(3) kg m^(-3)` तथा जल की संपीड़ता (compressibility) `45 . 8 xx 10^(-11) Pa^(-1) (1 atm = 1.013 xx 10^(5) Pa)`
06:13View Solution
1.10 प्रत्यास्थता questions and complete solutions for chapter सामान्य भौतिकी of DAS GUPTA of Class 11
All Exercises from BHARTI_BHAWAN Class 11 PHYSICS सामान्य भौतिकी
- 1 . 1 मात्रक और विमा : मापन एवं मापों में त्रुटियों
- 1 . 1 मात्रक और विमा : मापन एवं मापों में त्रुटियों (रिक्त स्थानों की पूर्ति करे )
- 1 . 13 बरनूली - प्रमेय : श्यानता
- 1. 9 गुरुत्वाकर्षण
- 1.10 प्रत्यास्थता
- 1.11 लघु दोलन : सरल आवर्त गति : लोलक
- 1.12 तरल दाब : पास्कल का नियम : पृष्ठ - तनाव
- 1.2 अदिश एवं सदिश
- 1.3 सरल रेखा एवं समतल में गति
- 1.4 गति के नियम : घर्षण
- 1.5 कार्य , शक्ति और ऊर्जा
- 1.6 वृत्तीय गति
- 1.7 आवेग एवं संवेग
- 1.8 द्रव्यमान केंद्र : घूर्णन
