Complete Solutions to 1.3 सरल रेखा एवं समतल में गति of chapter सामान्य भौतिकी of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | सामान्य भौतिकी |
| BHARTI_BHAWAN | 1.3 सरल रेखा एवं समतल में गति |
| Number Of Questions | 76 |
| Academic Year | 2023-24 |
यदि सरल रेखा में गतिशील किसी कण की स्थिति (x) को समय (t) के फलन (function) के रूप में निम्नांकित समीकरण में व्यक्त किया जाए
`x = 2t^(2) - 3t^(2) + 4t +1`
जहाँ x मीटर में, तथा t सेकण्ड में हो, तो निम्नांकित के मान ज्ञात करे -
समय t = 1 s पर कण की स्थितिView Solutionयदि सरल रेखा में गतिशील किसी कण की स्थिति (x) को समय (t) के फलन (function) के रूप में निम्नांकित समीकरण में व्यक्त किया जाए
`x = 2t^(3) - 3t^(2) + 4t +1`
जहाँ x मीटर में, तथा t सेकण्ड में हो, तो निम्नांकित के मान ज्ञात करे -
समय t = 2 s पर कण की चाल04:09View Solutionयदि सरल रेखा में गतिशील किसी कण की स्थिति (x) को समय (t) के फलन (function) के रूप में निम्नांकित समीकरण में व्यक्त किया जाए
`x = 2t^(2) - 3t^(2) + 4t +1`
जहाँ x मीटर में, तथा t सेकण्ड में हो, तो निम्नांकित के मान ज्ञात करे -
समय t = 3 s पर कण का त्वरण04:09View Solutionयदि सरल रेखा में गतिशील किसी कण की स्थिति (x) को समय (t) के फलन (function) के रूप में निम्नांकित समीकरण में व्यक्त किया जाए
`x = 2t^(2) - 3t^(2) + 4t +1`
जहाँ x मीटर में, तथा t सेकण्ड में हो, तो निम्नांकित के मान ज्ञात करे -
गति के क्रम में क्या किसी समय कण क्षणिक विराम (momentary rest ) में आएगा।View Solutionदो विद्यार्थी A और B अपने संस्थान (institute) O से लौटकर अपने - अपने घर P तथा Q को जा रहे है। इनकी गति को स्थिति - समय ग्राफ (position-time graph) , अर्थात x-t ग्राफ द्वारा चित्र 13.1 में प्रदर्शित किया गय्या है। निम्नांकित कोष्ठकों (brackets) से सही प्रविष्टियाँ (entries) बताएँ
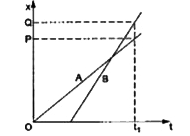
`(A//B)` की तुलना में `(B//A)` का घर संस्थान से निकट है।02:08View Solutionदो विद्यार्थी A और B अपने संस्थान (institute) O से लौटकर अपने - अपने घर P तथा Q को जा रहे है। इनकी गति को स्थिति - समय ग्राफ (position-time graph) , अर्थात x-t ग्राफ द्वारा चित्र 13.1 में प्रदर्शित किया गय्या है। निम्नांकित कोष्ठकों (brackets) से सही प्रविष्टियाँ (entries) बताएँ

`(A//B)` की तुलना में `(B//A)` संस्थान से पहले प्रस्थान करता है।01:42View Solutionदो विद्यार्थी A और B अपने संस्थान (institute) O से लौटकर अपने - अपने घर P तथा Q को जा रहे है। इनकी गति को स्थिति - समय ग्राफ (position-time graph) , अर्थात x-t ग्राफ द्वारा चित्र 13.1 में प्रदर्शित किया गय्या है। निम्नांकित कोष्ठकों (brackets) से सही प्रविष्टियाँ (entries) बताएँ
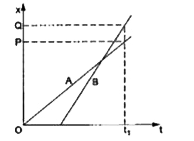
`(A//B)` की तुलना में `(B//A)` तेज चलता है।01:51View Solutionदो विद्यार्थी A और B अपने संस्थान (institute) O से लौटकर अपने - अपने घर P तथा Q को जा रहे है। इनकी गति को स्थिति - समय ग्राफ (position-time graph) , अर्थात x-t ग्राफ द्वारा चित्र 13.1 में प्रदर्शित किया गय्या है। निम्नांकित कोष्ठकों (brackets) से सही प्रविष्टियाँ (entries) बताएँ
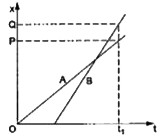
A और B दोनों (समान / भिन्न) समय पर घर पहुँचते है।01:40View Solutionदो विद्यार्थी A और B अपने संस्थान (institute) O से लौटकर अपने - अपने घर P तथा Q को जा रहे है। इनकी गति को स्थिति - समय ग्राफ (position-time graph) , अर्थात x-t ग्राफ द्वारा चित्र 13.1 में प्रदर्शित किया गय्या है। निम्नांकित कोष्ठकों (brackets) से सही प्रविष्टियाँ (entries) बताएँ
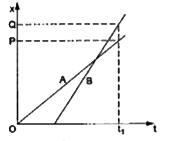
`(A//B)` अपने मार्ग पर `(B//A)` से ( एक बार / दो बार ) आगे हो जाते है03:03View Solutionएक आदमी अपने घर से प्राप्तः काल 9.00 बजे 2.5 km दूर स्थित अपने कार्यालय (office) के लिए सीधी सड़क पर `5 km h^(-1)` की एकसमान चाल (uniform speed ) से चलता है। वहाँ पर वह सांयकाल 5.00 बजे तक रहता है और अंत में वह `25 km h^(-1)` की चाल से किसी वाहन द्वारा अपने घर लौट आता है। उपयुक्त स्केल चुनकर उसकी गति का एक स्थिति - समय ग्राफ (position - time graph) अर्थात x-t ग्राफ खींचे
05:50View Solutionकोई शराबी (drunkard) किसी संकीर्ण गली (narrow lane) में 5 कदम (steps) आगे बढ़ता है और फिर 3 कदम पीछे आता है , उसके बाद फिर 5 कदम आगे और 3 कदम पीछे आता है , तथा इसी क्रम में वह आगे बढ़ता रहता है। उसका प्रत्येक कदम 1 m लंबा है जिसे तय करने में वह 1 s का समय लेता है। उसकी गति का एक स्थिति - समय ग्राफ (x - t graph) खींचे। ग्राफ से या किसी अन्य विधि से यह ज्ञात करे की अपने चलने के स्थान से 13 m की दुरी पर स्थित किसी गड्ढे (pit) में वह कितने समय के बाद गिर जाएगा ?
10:44View Solutionकोई जेट - विमान `500 km h^(-1)` की चाल से चल रहा है तथा उससे निष्कासित गैस जेट - विमान के सापेक्ष `1500 km h^(-1)` की चाल से बहार निकल रही है। धरती पर खड़े किसी प्रेक्षक (observer) के सापेक्ष निष्कासित गैस की चाल ज्ञात करे।
01:53View Solutionकिसी सरल रैखिक मार्ग पर `126 . 0 km h^(-1)` की चाल से गतिशील किसी वाइन को 200 m की दुरी तय करने पर विराम में लाया जाता है। यदि गति में मंदन (retardation) को एकसमान (uniform) मान ले तो मंदन का मान निकले। वाइन को विराम में आने के लिए कितना समय लगा ?
05:18View Solutionदो रेलगाड़ियाँ P तथा Q दो समांतर पटरियों (parallel tracks ) पर `72.0 km h^(-1)` की एकसमान चाल (uniform speed) से एक ही दिशा में गतिशील है दोनों की लंबाई 400 m है तथा Q की स्थिति P के पीछे है। Q का चालक (driver ) P से आगे निकलने के लिए गाड़ी में `1m s^(-2)` का त्वरण (acceleration) लगाता है। यदि 50 s के बाद Q का गार्ड P के इंजन से आगे निकल जाए तो दोनों अर्थात Q के गार्ड और P के इंजन के बीच प्रांरभिक दुरी (initial distance) ज्ञात करे।
10:38View Solutionदो लेनेवाली सड़क पर के वाहन `A 10 m s^(-1)` की एकसमान चाल से गतिशील है। अन्य दो वाहन B एवं C विपरीत दिशाओ में `15 m s ^(-1)` की समान चाल से चलते हुए वाहन A तक पहुँचने का प्रयास करते है। किसी क्षण जब दुरी AB, दुरी AC के बराबर है तथा दोनों के मान 1 km हो, वाहन B का चालक का निर्णय लेता है कि वाहन C के A तक पहुँचने के पहले ही वह वाहन A से आगे निकल जाए। वाहन B का न्यूनतम त्वरण ज्ञात करे ताकि वह किसी दुर्घटना से बच सके
05:47View Solutionकिसी पत्थर को उर्द्धवाधर : ऊपर की ओर (vertically upward) `29 . 4 m s^(-1)` के प्रारंभिक वेग से फेका जाता है -
ऊपर की ओर गति के क्रम में पत्थर के त्वरण की दिशा क्या होगी ?02:11View Solutionकिसी पत्थर को उर्द्धवाधर : ऊपर की ओर (vertically upward) `29 . 4 m s^(-1)` के प्रारंभिक वेग से फेका जाता है -
गति पथ के उच्चतम बिंदु पर पत्थर के वेग एवं त्वरण के मान क्या होंगे ?03:39View Solutionकिसी पत्थर को उर्द्धवाधर : ऊपर की ओर (vertically upward) `29 . 4 m s^(-1)` के प्रारंभिक वेग से फेका जाता है -
यदि उच्चतम बिंदु पर स्थिति (position) x तथा समय t के मान क्रमशः x = 0 तथा t = 0 मान ले, और ऊर्ध्वाधरतः नीचे ओर (vertically downward) की दिशा को x-अक्ष की धनात्मक दिशा (positive direction of x-aisx) मान ले तो गेंद की ऊपर की ओर तथा नीचे की ओर गति के क्रम में स्थिति , वेग एवं त्वरण के चिह्न (sign) बताएँ05:59View Solutionकिसी पत्थर को उर्द्धवाधर : ऊपर की ओर (vertically upward) `29 . 4 m s^(-1)` के प्रारंभिक वेग से फेका जाता है -
पत्थर द्वारा प्राप्त उच्चतम ऊँचाई (maximum height ) तथा पत्थर का उड़ान- काल (time of flight ) ज्ञात करे [`g = 9 . 8 m s^(-2)` तथा वायु प्रतिरोध = 0 ]View Solutionनिम्नांकित कथनो (statements) को ध्यानपूर्वक पढ़े तथा करण बताते हुए तथा उदाहरण देते हुए बताएँ कि वे सही है अथवा नहीं (true of false) ? एक - विमीय गति (one-dimensional motion) में किसी कण की
किसी समय चाल शून्य होने पर भी उसका त्वरण अशून्य (nonzero) हो सकता है।01:39View Solutionनिम्नांकित कथनो (statements) को ध्यानपूर्वक पढ़े तथा करण बताते हुए तथा उदाहरण देते हुए बताएँ कि वे सही है अथवा नहीं (true of false) ? एक - विमीय गति (one-dimensional motion) में किसी कण की
चाल शून्य होने पर भी उसका वेग अशून्य हो सकता है।02:07View Solutionनिम्नांकित कथनो (statements) को ध्यानपूर्वक पढ़े तथा करण बताते हुए तथा उदाहरण देते हुए बताएँ कि वे सही है अथवा नहीं (true of false) ? एक - विमीय गति (one-dimensional motion) में किसी कण की
चाल अचर (constant) हो, तो त्वरण अवश्य ही शून्य होना चाहिए।04:32View Solutionनिम्नांकित कथनो (statements) को ध्यानपूर्वक पढ़े तथा करण बताते हुए तथा उदाहरण देते हुए बताएँ कि वे सही है अथवा नहीं (true of false) ? एक - विमीय गति (one-dimensional motion) में किसी कण की
धनात्मक त्वरण के क्रम में चाल में हमेशा वृद्धि होती रहेगी07:42View Solutionकिसी पत्थर को 90 m की ऊँचाई के फर्श पर विरामावस्था से गिराया जाता है। फर्श के साथ टक्कर के क्रम में प्रत्येक बार पत्थर की चाल का 1/10 भाग कम हो जाता है। समयांतराल t = 0 से t = 12 s के बीच पत्थर की गति का चाल - समय ग्राफ (speed - time graph ) खींचे `(g = 9 . 8 m s^(-2))`
10:39View Solutionकोई व्यक्ति अपने निवास - स्थान से सीधी सड़क पर `5 km h^(-1)` की एकसमान चाल से चलकर 2 . 5 km की दुरी पर स्थित बाजार (market) पहुँचता है। अवकाश के कारण बाजार को बंद देखकर वह उसी समय मुड़कर `7 5 km h^(-1)` की एकसमान चाल से चलकर वापस घर लौट आता है। समयांतराल (i) 0 - 30 मिनट (ii) 0 - 50 मिनट (iii) 0 - 40 मिनट के बीच उस व्यक्ति के
(a) माध्य वेग का परिमाण , तथा
(b) माध्य चाल ज्ञात करे
[ नोट: इस उदाहरण से आपको स्पष्ट संकेत मिलेगा कि माध्य चाल को माध्य - वेग के परिमाण के रूप में परिभाषित करने कि अपेक्षा करने कि अपेक्षा कुल पथ की लंबाई को समयांतराल द्वारा विभाजित करना सही क्यों है। आप उस थके व्यक्ति को यह कदापि नहीं करना चाहेंगे कि उसकी माध्य चाल शून्य थी प्रश्न से दुरी चाल घर से बाजार पँहुचने में लगा समय दुरी चाल मिनट। फिर बाजार से घर पहुँचने में लगा समय दुरी चाल मिनट कुल समय मिनट मिनट मिनट।12:35View Solutionचित्र में प्रदर्शित (a) से (b) तक के ग्राफ को देखकर यह बताएँ कि इनमे से कौन- कौन - सा ग्राफ किसी कण कि एकविमीय गति को संभवतः नहीं व्यक्त करता है ? करणसहित स्पष्ट करे।
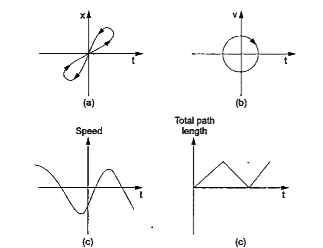 04:39View Solution
04:39View Solutionकिसी कण कि एकविमीय गति का x - t ग्राफ चित्र 1.3 - 6 द्वारा प्रदर्शित है। ग्राफ के अनुसार क्या यह कहना उचित होगा कि वह कण समय `t lt 0` के लिए किसी सरल रेखा में और `t gt 0` के लिए परवलीय पथ (parabolic path ) में गति करता है ? यदि नहीं , तो ग्राफ के संगत किसी उचित भौतिक संदर्भ (suitable physical context) बताएँ
 03:01View Solution
03:01View Solutionकिसी राजमार्ग पर पुलिस का कोई वाहन `30 km h^(-1)` की एकसमान चाल से चल रहा है और वह उसी दिशा में `192 km h^(-1)` की एकसमान चाल से जा रहे चोर के किसी अन्य वाहन का पीछा करते हुए उसपर गोली (bullet चलाता है। यदि गोली की नाल - मुखी चाल (muzzle speed) `150 m s^(-1)` हो, तो चोर की गाड़ी पर गोली किस चाल के साथ आघात करेगी ?
[ नोट : उस चाल की गणना करे जो चोर (thief) के वाहन की हानि पँहुचा रही हो। ]07:36View Solutionचित्र 1.3 - 7 में प्रदर्शित प्रत्येक ग्राफ से संबंधित किसी उचित भौतिक संदर्भ को स्पष्ट करे।
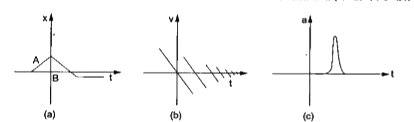 05:12View Solution
05:12View Solutionएक सरल रेखा पर सरल आवर्त गति (simple harmonic motion) निष्पन्न करते हुए किसी कण का x - t ग्राफ चित्र 1.3 - 8 में प्रदर्शित है (इस गति का पूर्ण विवरण अध्याय 11 में दिया गया है ) समय t = 0.3, 1.3 s, - 1.3 s पर कण के स्थिति , वेग एवं त्वरण के चिह्न क्या होंगे , धनात्मक अथवा ऋणात्मक ?
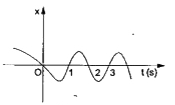 06:58View Solution
06:58View Solutionकिसी कण की एकविमीय गति का x - t ग्राफ चित्र 1.3 - 9 में प्रदर्शित है इसमें तीन समान समयांतराल (time interval) 1, 2 तथा 3 पर दिखाए गए है। किस अंतराल में माध्य चाल अधिकतम (maximum) है और किसमे न्यूनतम (minimum) ? प्रत्येक अंतराल में माध्य वेग (average velocity) का चिह्न (धनात्मक अथवा ऋणात्मक बताएँ )
 02:24View Solution
02:24View Solutionकिसी निश्चित दिशा में गतिशील कण के लिए चाल - समय ग्राफ (speed - time graph ) चित्र 1.3 - 10 में प्रदर्शित है। समान समयांतराल 1,2 ,3 में किस अंतराल में माध्य त्वरण का परिमाण अधिकतम होगा ? किस अंतराल में माध्य चाल (v) अधिकतम होगी ? धनात्मक दिशा (positive direction) को गति की निश्चित दिशा मानते हुए तीनो अंतरालों में v तथा a के चिह्न बताएँ A, B, C तथा D बिंदुओं पर त्वरण क्या होंगे ?
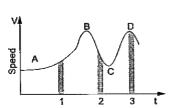 04:48View Solution
04:48View Solutionकोई वाहन विराम (rest) से किसी सीधी सड़क पर `1m s^(-2)-` के एकसमान त्वरण के साथ 10 s तक चलता है इसके बाद वह एकसमान वेग से चलता है। वाहन द्वारा nवे सेकंड (n = 1, 2 3, . . . ) में तय की गई दुरी तथा n बीच ग्राफ खींचे। आपके अनुसार त्वरित गति के क्रम में ग्राफ का स्वरूप सरल रेखा होगा या परवलय (parabola)
07:48View Solutionखुली छत (roof) वाली किसी स्थिर (stationary) लिफ्ट में खड़ा व्यक्ति एक गेंद को अपनी पूरी ताकत से ऊर्ध्वाधरतः ऊपर की ओर `49 m s^(-1)` प्रारंभिक चाल से फेकता है। कितने समय के बाद वह गेंद उस व्यक्ति के हाथो में पुनः लौटकर वापस आ जाएगी (अर्थात , गेंद का उड़ान - काल कितना होगा ) ? यदि लिफ्ट ऊपर की ओर `5 m s^(-1)` की एकसमान चाल से चलना शुरू कर दे और वह व्यक्ति पुनः अपनी उसी ताकत में उस गेंद को ऊपर की ओर फेकता हो, तो अब गेंद को उसके हाथो में लौटकर आने में कितना समय लगेगा ?
04:27View Solutionचित्र 1.3 - 12 में क्षैतिज दिशा में गतिशील कोई लंबा वेल्ट `4 km h ^(-1)` की एकसमान चाल से चल रहा है। एक बालक इस वेल्ट पर दो अन्य व्यक्तियों 1 एवं 2 के बीच वेल्ट के सापेक्ष `9 km h^(-1)` की चाल से कभी आगे कभी पीछे दौड़ रहा है। यदि व्यक्ति 1 एवं 2 के बीच की दुरी 50 m हो, तो बाहर स्थिर फर्श पर खड़े किसी स्थिर प्रेक्षक (stationary observer) के लिए निम्नांकित का मान ज्ञात करे।
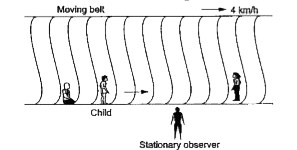
वेल्ट की गति की दिशा में दौड़ते बालक की चाल06:27View Solutionचित्र 1.3 - 12 में क्षैतिज दिशा में गतिशील कोई लंबा वेल्ट `4 km h ^(-1)` की एकसमान चाल से चल रहा है। एक बालक इस वेल्ट पर दो अन्य व्यक्तियों 1 एवं 2 के बीच वेल्ट के सापेक्ष `9 km h^(-1)` की चाल से कभी आगे कभी पीछे दौड़ रहा है। यदि व्यक्ति 1 एवं 2 के बीच की दुरी 50 m हो, तो बाहर स्थिर फर्श पर खड़े किसी स्थिर प्रेक्षक (stationary observer) के लिए निम्नांकित का मान ज्ञात करे।
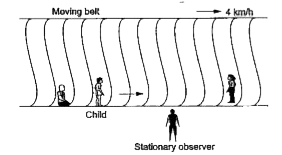
वेल्ट की गति की दिशा में विपरीत दौड़ते बालक की चाल06:27View Solutionचित्र 1.3 - 12 में क्षैतिज दिशा में गतिशील कोई लंबा वेल्ट `4 km h ^(-1)` की एकसमान चाल से चल रहा है। एक बालक इस वेल्ट पर दो अन्य व्यक्तियों 1 एवं 2 के बीच वेल्ट के सापेक्ष `9 km h^(-1)` की चाल से कभी आगे कभी पीछे दौड़ रहा है। यदि व्यक्ति 1 एवं 2 के बीच की दुरी 50 m हो, तो बाहर स्थिर फर्श पर खड़े किसी स्थिर प्रेक्षक (stationary observer) के लिए निम्नांकित का मान ज्ञात करे।
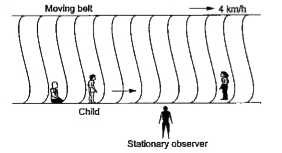
बालक द्वारा (a) एवं (b) में लिया गया समय
यदि बालक की गति का प्रेक्षण व्यक्ति 1 या 2 द्वारा किया जाए तो कौन - सा उत्तर बदल जाएगा ?06:27View Solutionकिसी 200 m ऊँची चट्टान के ऊपरी सिरे से दो पत्थरो को एक साथ क्रमशः `15 m s^(-1)` तथा `30 m s^(-1)` की प्रारंभिक चाल से ऊर्ध्वाधरतः ऊपर की ओर (vertically upward) फेंका जाता है। इस तथ्य का सत्यापन करे (verify ) कि चित्र 1.3 - 13 में प्रदर्शित ग्राफ पहले पत्थर के सापेक्ष दूसरे पत्थर कि आपेक्षिक स्थिति (relative position) का समय के साथ विचरण (variation) को सही रूप में व्यक्त करता है। (मान ले कि वायु प्रतिरोध नगण्य है और फर्श से टक्कर के बाद पत्थर तत्काल स्थिर हो जाते है , ऊपर कि ओर उछलते नहीं तथा `g = 10 m s^(-2)` ) ग्राफ के रेखीय (linear) एवं वक्रीय (curved) भागो के लिए समीकरण लिखे
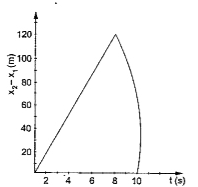 09:17View Solution
09:17View Solutionकिसी निश्चित दिशा में अनुरेख (along) गतिमान किसी कण के लिए चाल - समय ग्राफ (speed-time graph ) चित्र 1.3 - 14 में प्रदर्शित है। कण द्वारा (a) समयांतराल t = 0 से t = 10 s तथा (b) t = 2 s से t = 6 s के बीच तय कि गई दुरी ज्ञात करे ।
(a) एवं (b) में दिए गए संमयान्तरालों के दरम्यान कण कि माध्य चाल (average speed) भी ज्ञात करे
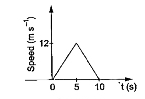 11:58View Solution
11:58View Solutionएक विमीय गति में किसी कण का वेग - समय ग्राफ चित्र 3.62 में दिखाया गया है नीचे दिए सूत्रों में `t_(1)` से `t_(2)` तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन-से सूत्र सही है
`x(t_(2))=x(t_(1))+v(t_(1))(t_(2)-t_(1))+(1//2)a(t_(2)-t_(1))^(2)`
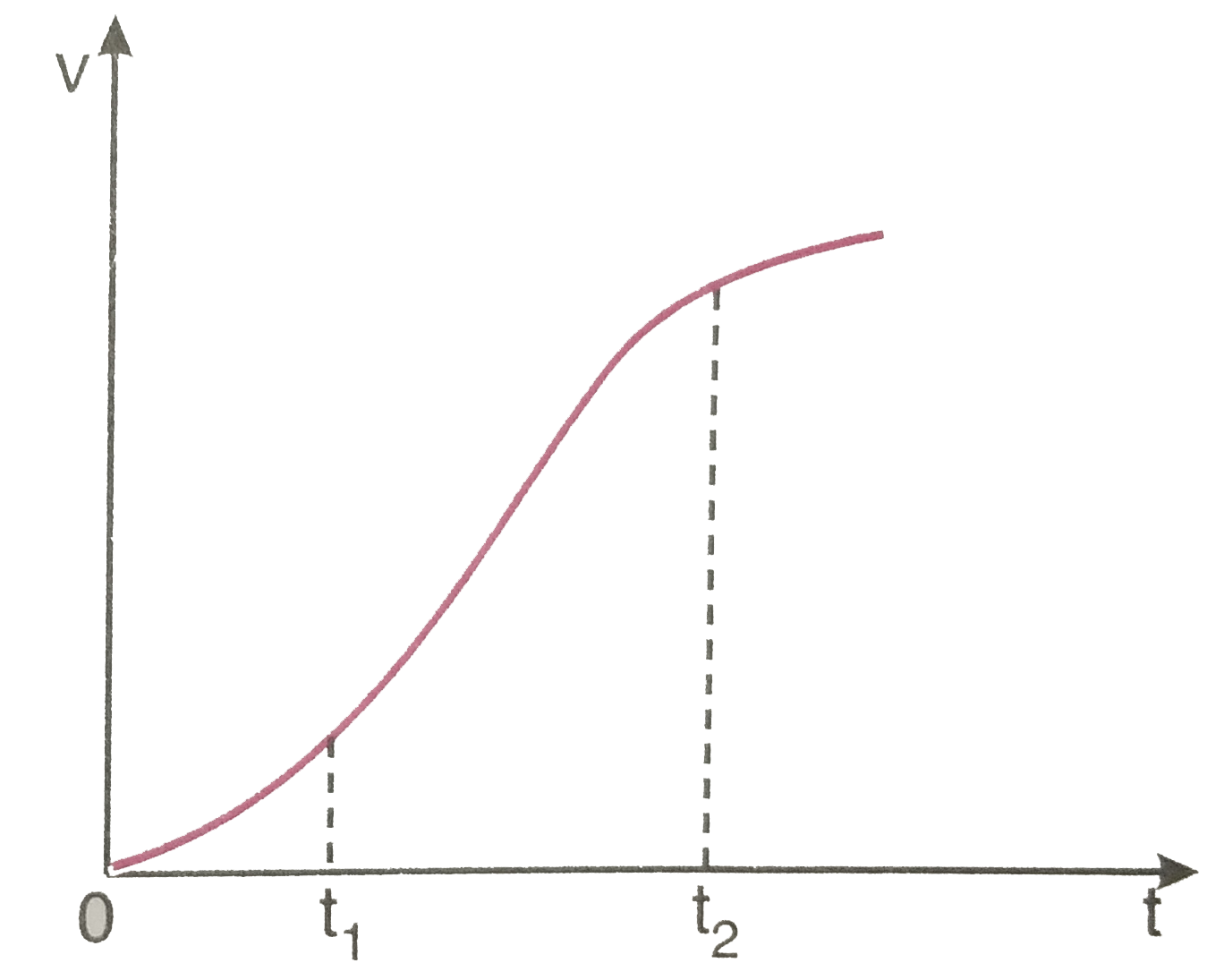 03:35View Solution
03:35View Solutionएकविमीय गति में किसी कण का वेग - समय ग्राफ (velocity - time graph ) चित्र 1.3 - 15 में प्रदर्शित है । समयांतराल `t_(1)` से `t_(2)` के बीच कण कि गति को व्यक्त करने के लिए निम्नांकित सूत्रों में सही सूत्रों को चुने।
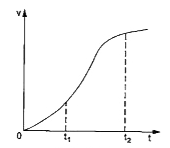
`v(t_(2)) = v (t_(1)) + a (t_(2) - t_(1))`View Solutionएकविमीय गति में किसी कण का वेग - समय ग्राफ (velocity - time graph ) चित्र 1.3 - 15 में प्रदर्शित है । समयांतराल `t_(1)` से `t_(2)` के बीच कण कि गति को व्यक्त करने के लिए निम्नांकित सूत्रों में सही सूत्रों को चुने।
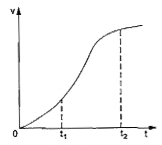
`v_("average")=(x(t_(2))- x (t_(1)))/(t_(2) - t_(1))`03:27View Solutionएकविमीय गति में किसी कण का वेग - समय ग्राफ (velocity - time graph ) चित्र 1.3 - 15 में प्रदर्शित है । समयांतराल `t_(1)` से `t_(2)` के बीच कण कि गति को व्यक्त करने के लिए निम्नांकित सूत्रों में सही सूत्रों को चुने।
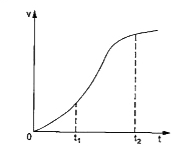
`a_("average") = (v(t_(2))-v(t_(1)))/((t_(2)-t_(1)))`03:03View Solutionएक विमीय गति में किसी कण का वेग - समय ग्राफ चित्र 3.62 में दिखाया गया है नीचे दिए सूत्रों में `t_(1)` से `t_(2)` तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन-से सूत्र सही है
`x(t_(2))=x(t_(1))+v(t_(1))(t_(2)-t_(1))+(1//2)a(t_(2)-t_(1))^(2)`
 03:35View Solution
03:35View Solutionएक विमीय गति में किसी कण का वेग - समय ग्राफ चित्र 3.62 में दिखाया गया है नीचे दिए सूत्रों में `t_(1)` से `t_(2)` तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन-से सूत्र सही है
`v(t_(2))=v(t_(1))+a(t_(2)-t_(1))`
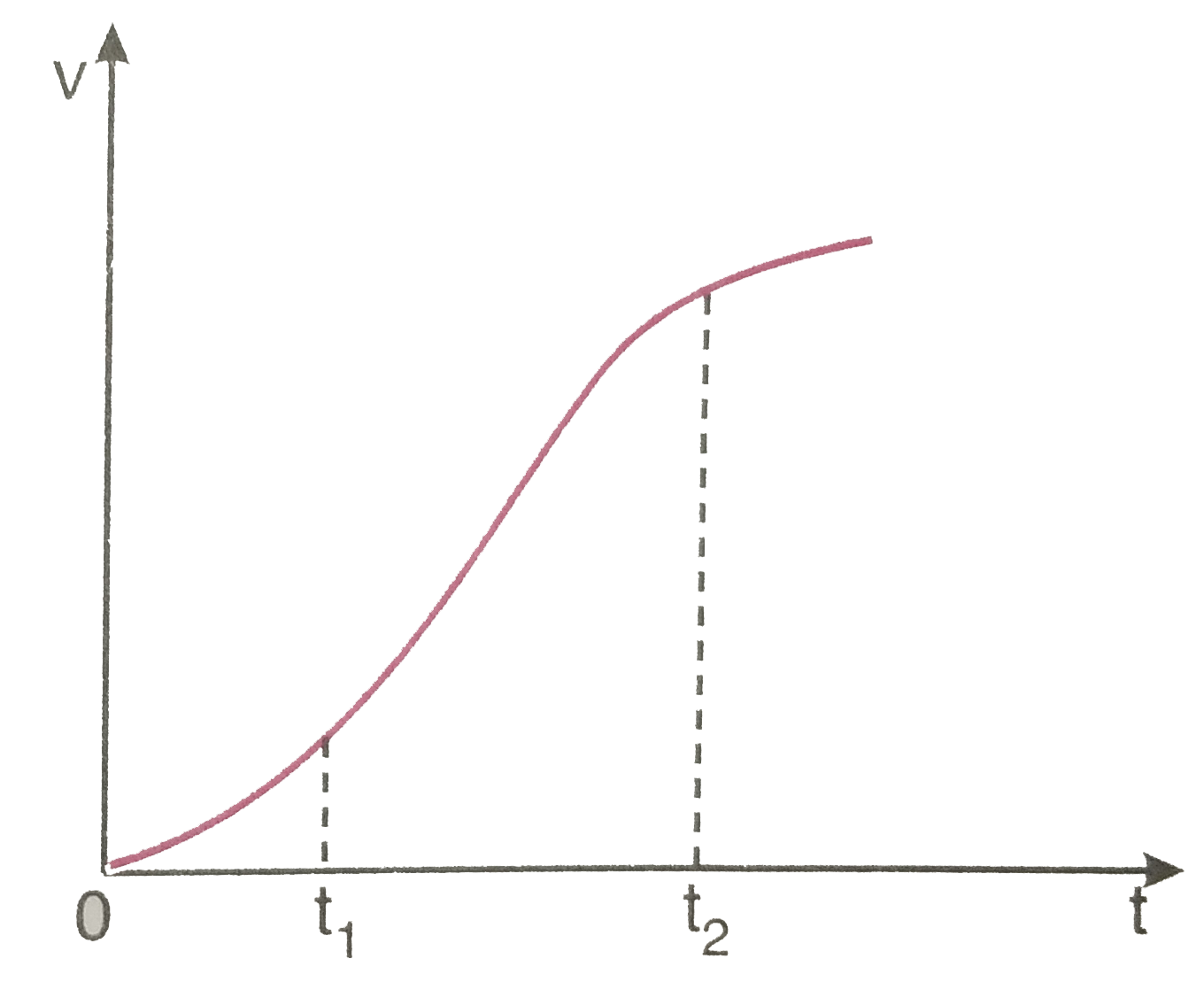 02:59View Solution
02:59View Solutionसरल रेखा पर गतिशील किसी कण कि चाल (v) का विचरण समय (t) एक सापेक्ष चित्र 1.3 - 16 में दिखाया गया है। निम्नांकित के मान ज्ञात करे।
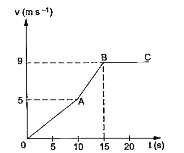
कण द्वारा प्रारंभ के 10 s में तय की गई दुरी01:53View Solutionसरल रेखा पर गतिशील किसी कण कि चाल (v) का विचरण समय (t) एक सापेक्ष चित्र 1.3 - 16 में दिखाया गया है। निम्नांकित के मान ज्ञात करे।

प्रारंभ के 15 s में तय की गई दुरी02:56View Solutionसरल रेखा पर गतिशील किसी कण कि चाल (v) का विचरण समय (t) एक सापेक्ष चित्र 1.3 - 16 में दिखाया गया है। निम्नांकित के मान ज्ञात करे।
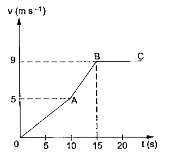
t = 5 s तथा t = 12 s का कण त्वरण03:32View Solutionसरल रेखा पर गतिशील किसी कण कि चाल (v) का विचरण समय (t) एक सापेक्ष चित्र 1.3 - 16 में दिखाया गया है। निम्नांकित के मान ज्ञात करे।
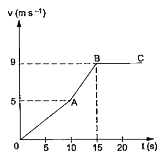
15 s से 20 s के दरम्यान तय की गई दुरी02:28View Solutionसरल रेखा पर गतिशील किसी कण कि चाल (v) का विचरण समय (t) एक सापेक्ष चित्र 1.3 - 16 में दिखाया गया है। निम्नांकित के मान ज्ञात करे।
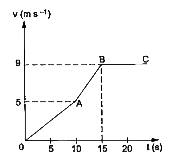
20 s पर कण का त्वरण01:53View Solutionचित्र 1. 3 - 17 में एक वृत्ताकार पार्क दिखाया गया है जिसकी परिधि `2 pi` km है। एक साईकिल सवार केंद्र O से चलना शुरू करता है और पार्क की सीमा (boundary) P पर पहुँचकर पार्क की परिधि के अनुदिश होता हुआ अंततः QO के रास्ते केंद्र O पर लौट जाता है। यदि इस पूरी यात्रा OPQO में 10 मिनट का समय लगा हो, तो इस गति के लिए निम्नांकित का मान निकाले

कुल विस्थापन का परिमाण04:01View Solutionचित्र 1. 3 - 17 में एक वृत्ताकार पार्क दिखाया गया है जिसकी परिधि `2 pi` km है। एक साईकिल सवार केंद्र O से चलना शुरू करता है और पार्क की सीमा (boundary) P पर पहुँचकर पार्क की परिधि के अनुदिश होता हुआ अंततः QO के रास्ते केंद्र O पर लौट जाता है। यदि इस पूरी यात्रा OPQO में 10 मिनट का समय लगा हो, तो इस गति के लिए निम्नांकित का मान निकाले

माध्य वेग तथा04:19View Solutionचित्र 1. 3 - 17 में एक वृत्ताकार पार्क दिखाया गया है जिसकी परिधि `2 pi` km है। एक साईकिल सवार केंद्र O से चलना शुरू करता है और पार्क की सीमा (boundary) P पर पहुँचकर पार्क की परिधि के अनुदिश होता हुआ अंततः QO के रास्ते केंद्र O पर लौट जाता है। यदि इस पूरी यात्रा OPQO में 10 मिनट का समय लगा हो, तो इस गति के लिए निम्नांकित का मान निकाले

माध्य चाल06:04View Solutionकिसी खुले मैदान में कोई स्कूटर - चालक एक ऐसे मार्ग से होकर चलता है जो प्रत्येक 0.50 km के सरल रैखिक पथ के बाद उसके बाई ओर `60^(@)` के कोण पर मुद जाता है। किसी एक मोड़ से गति प्रारंभ करने के क्रम में चालक का तीसरे , छठे एवं आठवे मोड़ पर पहुँचने पर विस्थापन का परिमाण ज्ञात करे। प्रत्येक अवस्था के लिए चालक द्वारा इन मोड़ो पर पहुँचने पर तय की गई कुल पथ - लंबाई एवं विस्थापन के परिमाण के बीच तुलना करे
09:09View Solutionकोई यात्री दिल्ली रेलवे स्टेशन पर पहुँचकर स्टेशन से किसी सीधी सड़क पर स्थिर एक होटल जो 10 km की दुरी पर है जाना चाहता है कोई ऑटो चालक अधिक पैसा ऐठने के लिए उसे अन्य की टेढ़े - मेढ़े मार्ग से 23 km का चक्कर लगाकर मिनट में होटल तक पहुँचा देता है।
ऑटो की माध्य चाल , और02:21View Solutionकोई यात्री दिल्ली रेलवे स्टेशन पर पहुँचकर स्टेशन से किसी सीधी सड़क पर स्थिर एक होटल जो 10 km की दुरी पर है जाना चाहता है कोई ऑटो चालक अधिक पैसा ऐठने के लिए उसे अन्य की टेढ़े - मेढ़े मार्ग से 23 km का चक्कर लगाकर मिनट में होटल तक पहुँचा देता है।
माध्य वेग का परिमाण ज्ञात करे। क्या वे एक - दूसरे के बराबर है ? यदि नहीं, तो वेग का परिमाण अधिक है या उसकी चाल ?02:21View Solutionवर्षा की बुँदे `30 m s^(-1)` के एकसमान वेग से ऊर्ध्वाधरतः नीचे आ रही है। यदि कोई व्यक्ति `10 m s^(-1)` के एकसमान वेग से उत्तर से दक्षिण की ओर साईकिल चलाता हुआ जा रहा हो, तो उसे अपने - आपको वर्षा से बचाने के लिए अपना छाता किस दिशा में रखना चाहिए ?
05:20View Solutionकोई व्यक्ति नहीं के शांत पानी में `4 km h^(-1)` की चाल से तैर सकता है। उसे 1000 m चौड़ी नदी को पार करने में कितना समय लगेगा , यदि नहीं का एकसमान बहाव - वेग ( flow speed) `3 km h ^(-1)` हो तथा व्यक्ति नहीं के बहाव की लंबवत दिशा में तैर रहा हो। नदी के दूसरे किनारे पर पहुँचने पर बहाव की दिशा में कितना बहाव (drift) करेगा ?
07:15View Solutionकिसी बदरगाह (harbour) खड़े किसी जहाज के ऊपर लगा झंडा `72 km h^(-1)` की चाल से बहती हुई हवा के कारण उत्तर - पूर्व दिशा में लहरा रहा है। यदि जहाज उत्तर दिशा में `51 km h^(-1)` की एकसमान चाल से चलना प्रारंभ कर दे तो बताएँ की जहाज पर लगा झंडा अब किस दिशा में लहराएगा ?
08:01View Solutionकिसी लंबे सभागृह (auditorium) के छत की ऊँचाई 25 m है `40 m s^(-1)` की चाल से प्रक्षेपित किसी गेंद द्वारा प्राप्त अधिकतम क्षैतिज दुरी कितनी होगी, यदि वह छत से बिना टकराए गुजर जाए ?
06:07View Solutionयदि एक व्यक्ति किसी पत्थर को 100 m की अधिकतम क्षैतिज दुरी (maximum horizontal range) तक फेक सकता हो , तो वही व्यक्ति उसी पत्थर को उसी स्थान के ऊर्ध्वाधरतः कितनी ऊँचाई तक फेक सकता है ?
01:57View Solutionकिसी कण की गति में इसका स्थिति सदिश (position vector) `vec(r)` को समय t के फलन (function) के रूप में निम्नांकित संबंध द्वारा व्यक्त किया गया है।
`vec(r) = ( 3 t hat(i) - 2 t ^(2) hat(j) + 4 hat(k))` m , जहाँ समय सेकंड में है तथा सभी गुणाको (coefficients) के मात्रक इस प्रकार से है कि `vec(r)` का मात्रक मीटर रहे।
कण का `vec(v)` तथा `vec(a)` ज्ञात करे , तथा02:40View Solutionकिसी कण की गति में इसका स्थिति सदिश (position vector) `vec(r)` को समय t के फलन (function) के रूप में निम्नांकित संबंध द्वारा व्यक्त किया गया है।
`vec(r) = ( 3 t hat(i) - 2 t ^(2) hat(j) + 4 hat(k))` m , जहाँ समय सेकंड में है तथा सभी गुणाको (coefficients) के मात्रक इस प्रकार से है कि `vec(r)` का मात्रक मीटर रहे।
समय t = 2 s पर कण कि तात्कालिक वेग का परिमाण तथा दिशा ज्ञात करे04:02View Solutionएक कण समय t = 0 पर मूलबिंदु (origin) से `10 hat(j) m s ^(-1)` के प्रारंभिक वेग से चलना शुरू करता है तथा x - y ताल में इसका एकसमान त्वरण `a = ( 8 hat(i) + 2 hat(j)) m s^(-2)` है
समय t के किस मान पर कण का x-निर्देशांक (x- coordinate) 16 m होगा ? उसी समय इसका y-निर्देशांक कितना होगा ?04:23View Solutionएक कण समय t = 0 पर मूलबिंदु (origin) से `10 hat(j) m s ^(-1)` के प्रारंभिक वेग से चलना शुरू करता है तथा x - y ताल में इसका एकसमान त्वरण `a = ( 8 hat(i) + 2 hat(j)) m s^(-2)` है
समय t के इसी मान पर कण की चाल कितनी होगी ?04:23View Solutionआकाश (space) में किसी स्वेच्छ गति (arbitrary motion) के लिए निम्नांकित संबंधो में से कौन- कौन सही है ?
`vec(v)_(av) = (1)/(2) [vec(v) (t_(1)) + vec(v) (t_(2))]`
[उपर्युक्त संबंधो में av (अर्थात average, या माध्य ) का अर्थ है वेग `(vec(v))` अथवा त्वरण `(vec(a))` का माध्य - मान समयांतराल `(t_(2) - t_(1))` के बीच]01:50View Solutionआकाश (space) में किसी स्वेच्छ गति (arbitrary motion) के लिए निम्नांकित संबंधो में से कौन- कौन सही है ?
` vec(v)_(av) = (vec(r) (t_(2))- vec(r) (t_(1)))/((t_(2) - t_(1)))`
[उपर्युक्त संबंधो में av (अर्थात average, या माध्य ) का अर्थ है वेग `(vec(v))` अथवा त्वरण `(vec(a))` का माध्य - मान समयांतराल `(t_(2) - t_(1))` के बीच]02:59View Solutionआकाश (space) में किसी स्वेच्छ गति (arbitrary motion) के लिए निम्नांकित संबंधो में से कौन- कौन सही है ?
`vec(v) (t) = vec(r) (0) + vec(a)*t`
[उपर्युक्त संबंधो में av (अर्थात average, या माध्य ) का अर्थ है वेग `(vec(v))` अथवा त्वरण `(vec(a))` का माध्य - मान समयांतराल `(t_(2) - t_(1))` के बीच]02:11View Solutionआकाश (space) में किसी स्वेच्छ गति (arbitrary motion) के लिए निम्नांकित संबंधो में से कौन- कौन सही है ?
`vec(r) (t) = vec(r) (0) + vec(v) (0) * 1 + (1)/(2) vec(a) * t^(2)`
[उपर्युक्त संबंधो में av (अर्थात average, या माध्य ) का अर्थ है वेग `(vec(v))` अथवा त्वरण `(vec(a))` का माध्य - मान समयांतराल `(t_(2) - t_(1))` के बीच]05:10View Solutionआकाश (space) में किसी स्वेच्छ गति (arbitrary motion) के लिए निम्नांकित संबंधो में से कौन- कौन सही है ?
`vec(a)_(av) = (vec(v)(t_(2)) - vec(v) (t_(1)))/(t_(2) - t_(1))`
[उपर्युक्त संबंधो में av (अर्थात average, या माध्य ) का अर्थ है वेग `(vec(v))` अथवा त्वरण `(vec(a))` का माध्य - मान समयांतराल `(t_(2) - t_(1))` के बीच]01:57View Solutionएक वायुयान पृथ्वी से 3.40 की ऊँचाई पर एकसमान चाल से क्षैतिजतः उड़ रहा है । यदि पृथ्वी के किसी प्रेक्षण - बिंदु (point of observation) पर वायुमान द्वारा 10 s में तय की गई दुरी की स्थितियाँ (positions) `30^(@)` का कोण बनाती हो, तो वायुमान की साल ज्ञात करे
02:02View Solutionप्रक्षेप्य गति में यदि प्रक्षेपण वेग के x- तथा y- घटक `v_(ax)` तथा `v_(ay)` हो, तो किसी समय के लिए इसके तात्क्षणिक वेग एवं क्षैतिज डिसा ( x-अक्ष) के बीच कोण `theta` को समय के निम्नलिखित फलन के रूप में व्यक्त करे
`theta (t) = tan^(-1) ((v_(ay) - g t)/(v_(ax)))`04:37View Solutionयदि प्रक्षेप्य का क्षैतिज पारस R तथा महत्तम ऊँचाई H हो, तो सिद्ध करे कि प्रक्षेपण कोण का मान
`theta _(0) = tan^(-1) ((4H)/(R))`View Solutionक्षैतिज तल से `30^(@)` के कोण की दिशा में कोई गोला जमीन से प्रक्षेपित किया जाता है जो उस स्थान से जमीन पर 3 . 0 km पर गिरता है। क्या यह संभव है कि प्रक्षेप कोण को समायोजित कर वह गोला 5 km की दुरी पर स्थित लक्ष्य को भेद सके ? मान ले कि गोले कि चाल नियत है तथा वायु प्रतिरोध नगण्य है ?
04:10View Solutionकोई लड़ाकू विमान क्षैतिज दिशा में जमीन से 1.5 km की ऊँचाई पर `720 k m h ^(-1)` की एकसमान चाल से उड़ रहा है और धरती पर स्थिर किसी तोप के ठीक ऊपर से गुजरता है।
तोप की नाल को ऊर्ध्वाधर से कितने कोण पर समायोजित करना चाहिए ताकि इसके द्वारा `600 m s^(-1)` की चाल से दागा गया गोला लड़ाकू विमान को क्षतिग्रस्त कर सके ?07:22View Solutionकोई लड़ाकू विमान क्षैतिज दिशा में जमीन से 1.5 km की ऊँचाई पर `720 k m h ^(-1)` की एकसमान चाल से उड़ रहा है और धरती पर स्थिर किसी तोप के ठीक ऊपर से गुजरता है।
विमान के चालक को अपना विमान किस न्यूनतम ऊँचाई पर उड़ाना चाहिए ताकि वह गोला लगने के बच सके `(g = 10 m s^(-2))`06:44View Solution
1.3 सरल रेखा एवं समतल में गति questions and complete solutions for chapter सामान्य भौतिकी of DAS GUPTA of Class 11
All Exercises from BHARTI_BHAWAN Class 11 PHYSICS सामान्य भौतिकी
- 1 . 1 मात्रक और विमा : मापन एवं मापों में त्रुटियों
- 1 . 1 मात्रक और विमा : मापन एवं मापों में त्रुटियों (रिक्त स्थानों की पूर्ति करे )
- 1 . 13 बरनूली - प्रमेय : श्यानता
- 1. 9 गुरुत्वाकर्षण
- 1.10 प्रत्यास्थता
- 1.11 लघु दोलन : सरल आवर्त गति : लोलक
- 1.12 तरल दाब : पास्कल का नियम : पृष्ठ - तनाव
- 1.2 अदिश एवं सदिश
- 1.3 सरल रेखा एवं समतल में गति
- 1.4 गति के नियम : घर्षण
- 1.5 कार्य , शक्ति और ऊर्जा
- 1.6 वृत्तीय गति
- 1.7 आवेग एवं संवेग
- 1.8 द्रव्यमान केंद्र : घूर्णन
