Complete Solutions to C Comprehension Type Questions of chapter WORK, POWER AND ENERGY of Class 11 book with complete answers and questions

A ball is released from point A as shown in figure. The ball leaves the track at B. All surfaces are smooth.

Let h be the maximum height from ground reached by ball after leaving track at B. Then,

A ball is released from point A as shown in figure. The ball leaves the track at B. All surfaces are smooth.

If track makes an angle `30^(@)` with horizontal at B, then maximum height attained by ball will be

In the figure shown, upper block is given a velocity of `6 m//s` and lower block. `3 m//s`. When relative motion between them is stopped

In the figure shown, upper block is given a velocity of `6 m//s` and lower block. `3 m//s`. When relative motion between them is stopped

A ball is released from the bottom of a tank filled with water up to 2m. On reaching the top its kinetic energy is found to be 16 J. Mass of the ball is 2 kg.
Ignoring the viscosity, let `W_(1)` be the work done by upthrust and `W_(2)` the work done by gravity, then `(g = 10 m//s^(2))`

A ball is released from the bottom of a tank filled with water up to 2m. On reaching the top its kinetic energy is found to be 16 J. Mass of the ball is 2 kg.
Ignoring the viscosity, let `W_(1)` be the work done by upthrust and `W_(2)` the work done by gravity, then `(g = 10 m//s^(2))`

The system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is `10 N//m`.

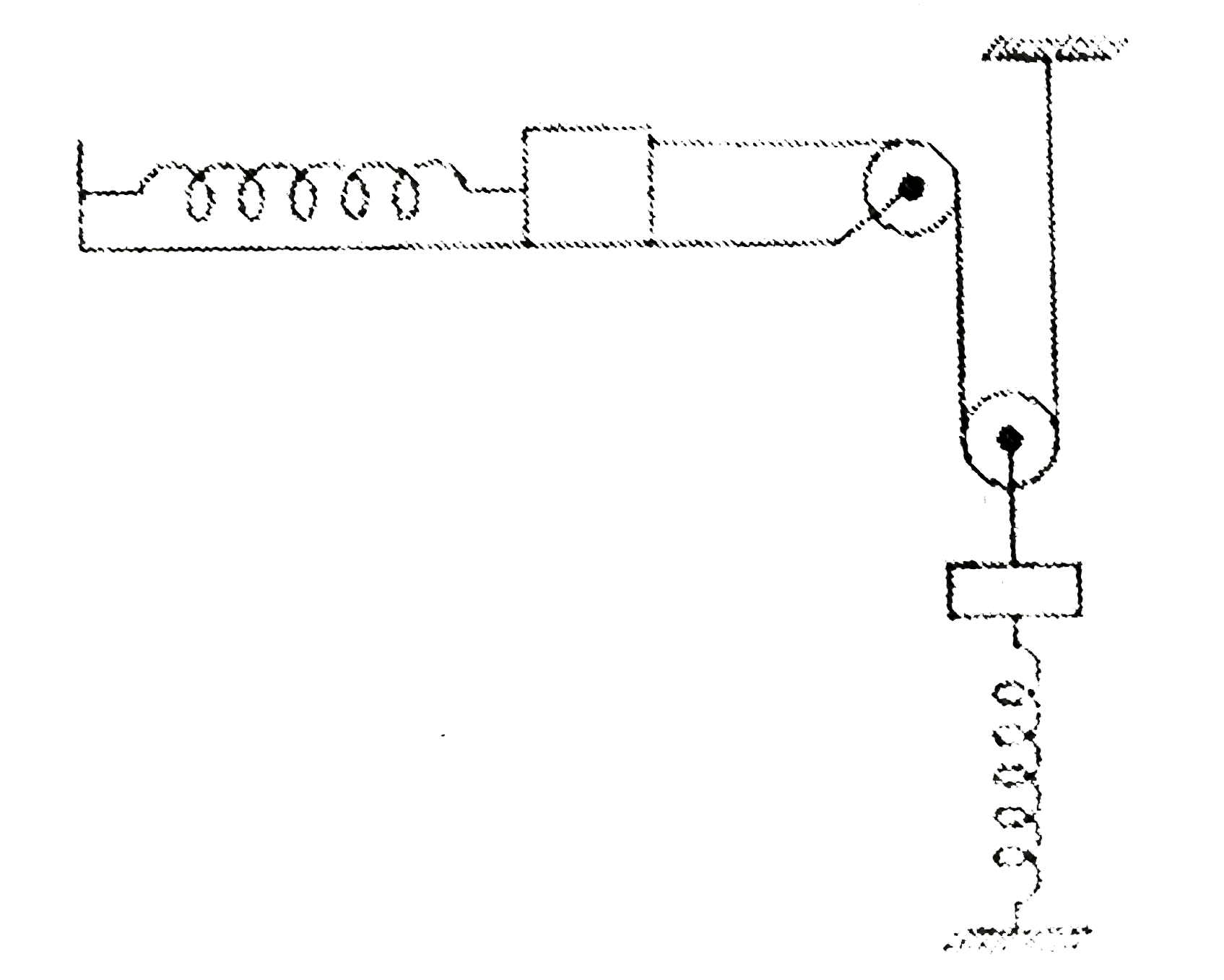
Extension of horizontal spring in equilibrium is

The system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is `10 N//m`.

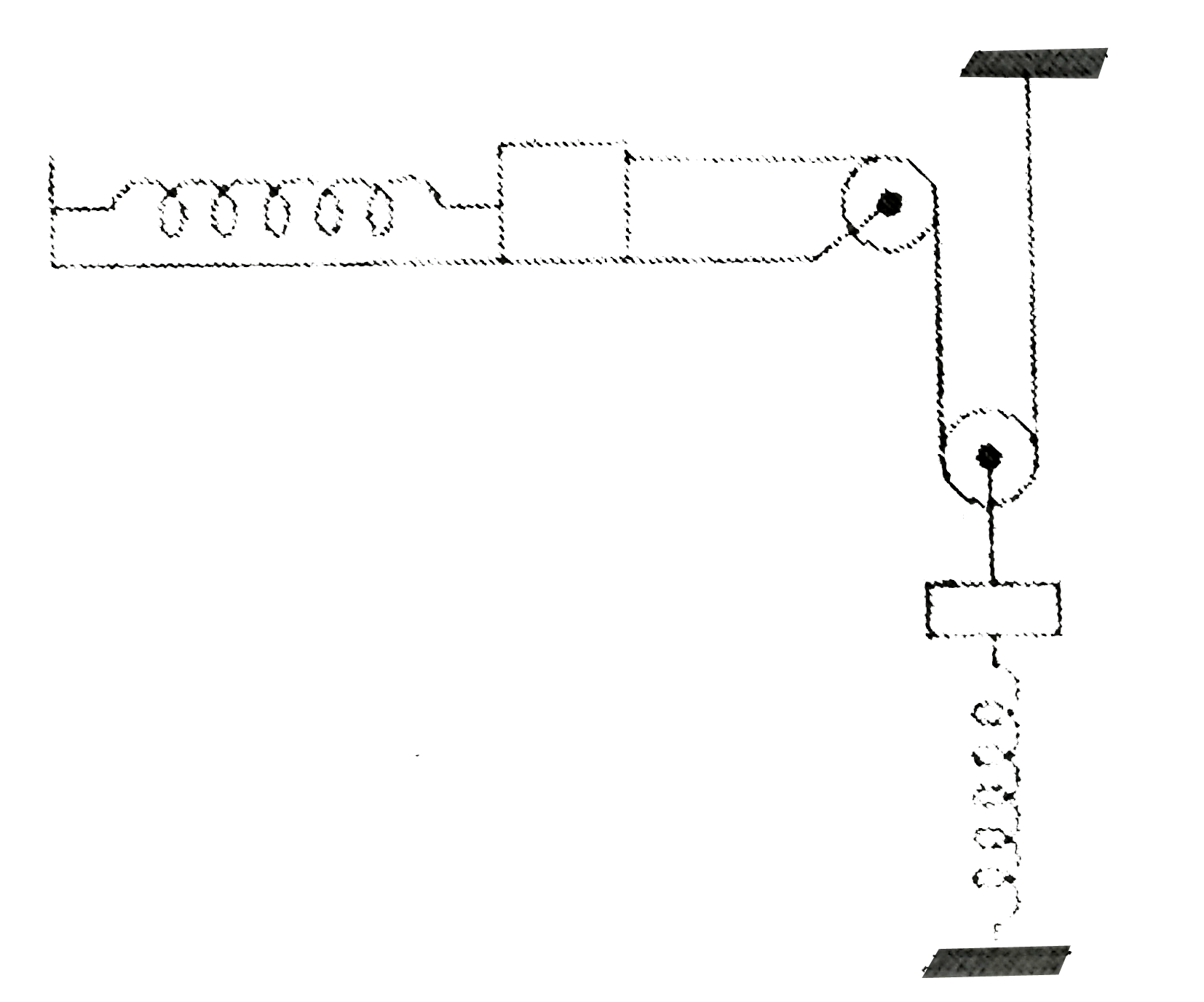
In the equilibrium position, speed of the block placed horizontally is

In a conservative force field we can find the radial component of force from the potential energy function by using `F = -(dU)/(dr)`. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : `U(r )=(A)/(r^(2))-(B)/(r )` where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The equilibrium distance is given by

In a conservative force field we can find the radial component of force from the potential energy function by using `F = -(dU)/(dr)`. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : `U(r )=(A)/(r^(2))-(B)/(r )` where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The equilibrium is

In a conservative force field we can find the radial component of force from the potential energy function by using `F = -(dU)/(dr)`. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : `U(r )=(A)/(r^(2))-(B)/(r )` where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The work required to move the particle from equilibrium distance to infinity is

In a conservative force field we can find the radial component of force from the potential energy function by using `F = -(dU)/(dr)`. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : `U(r )=(A)/(r^(2))-(B)/(r )` where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
If the total energy of the particle is `E=-(3B^(2))/(16A)`, and it is known that the motion is radial only then the velocity is zero at

In the figure, the variation of potential energy of a particle of mass m = 2kg is represented with respect to its x-coordinate. The particle moves under the effect of this conservative force along the X-axis.

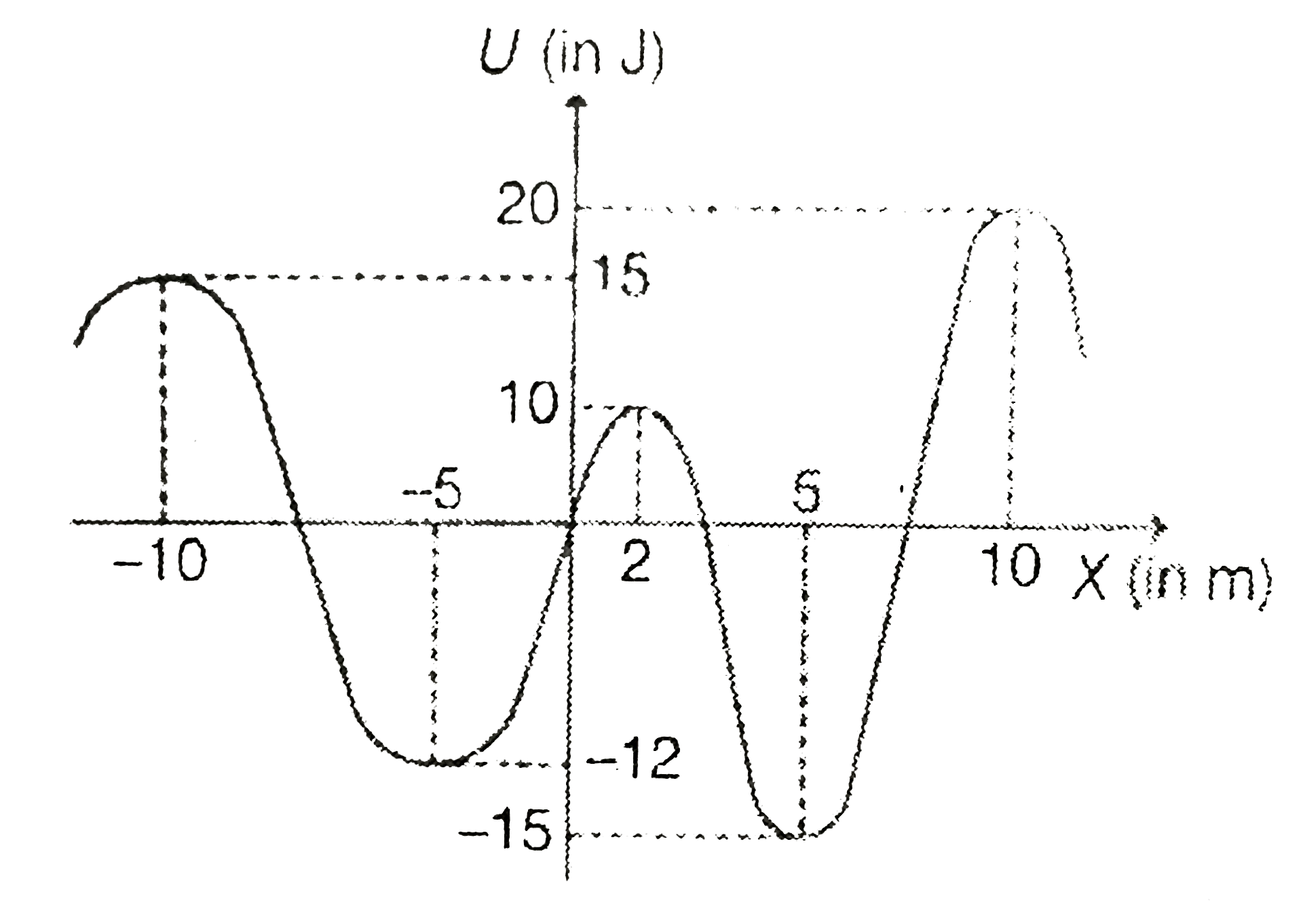
If the particle is released at the origin, then
(A)it will move towards positive x-axis
(B)it will move towards negative x-axis
(C)it will remain stationary at the origin
(D)Either of (a) or (b)

In the figure, the variation of potential energy of a particle of mass m = 2kg is represented with respect to its x-coordinate. The particle moves under the effect of this conservative force along the X-axis.

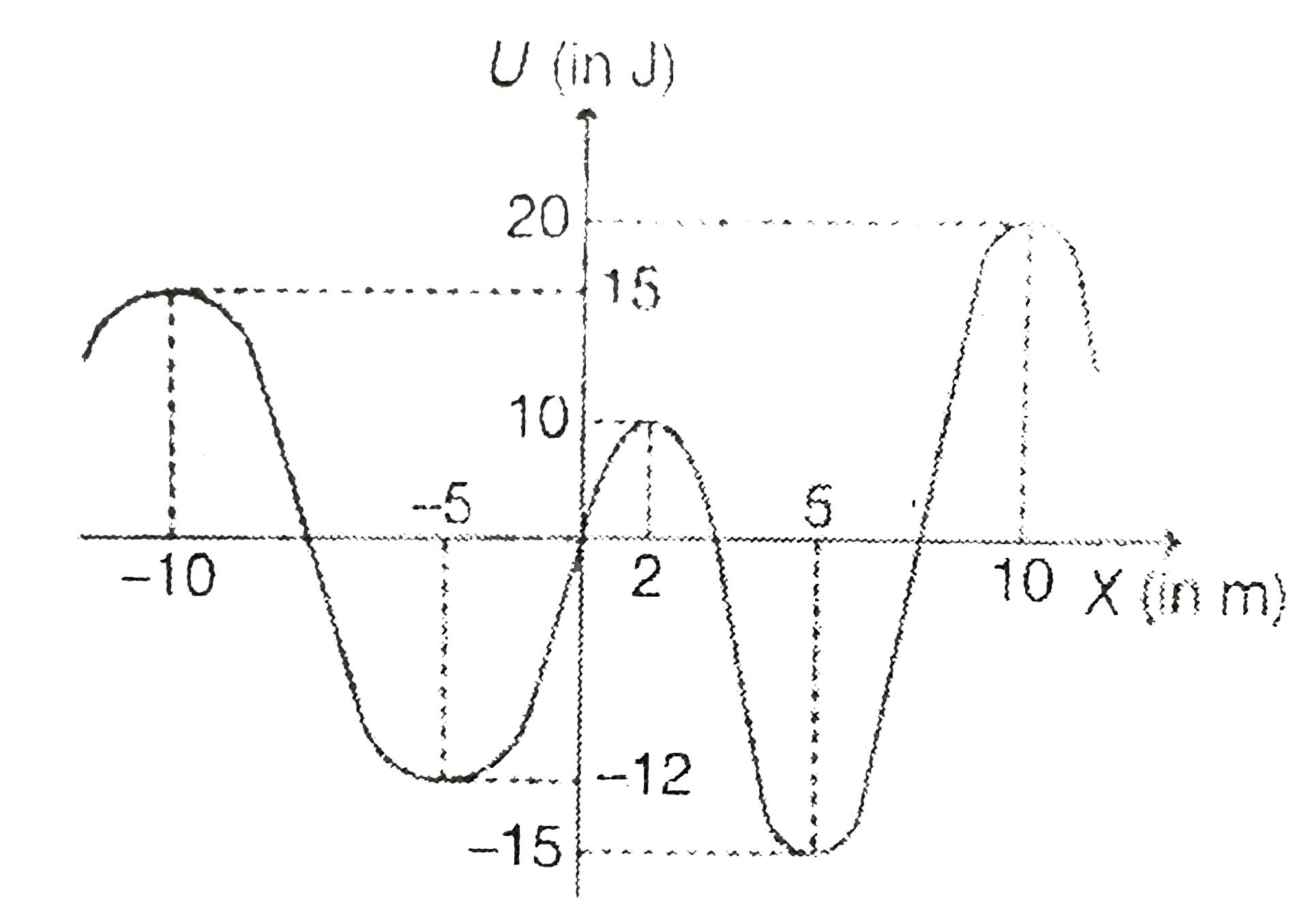
If the particle is released at `x = 2 + Delta` where `Delta rarr 0` (it is positive), then its maximum speed in subsequent motion will be

In the figure the variation of potential energy of a particle of mass `m = 2kg` is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.

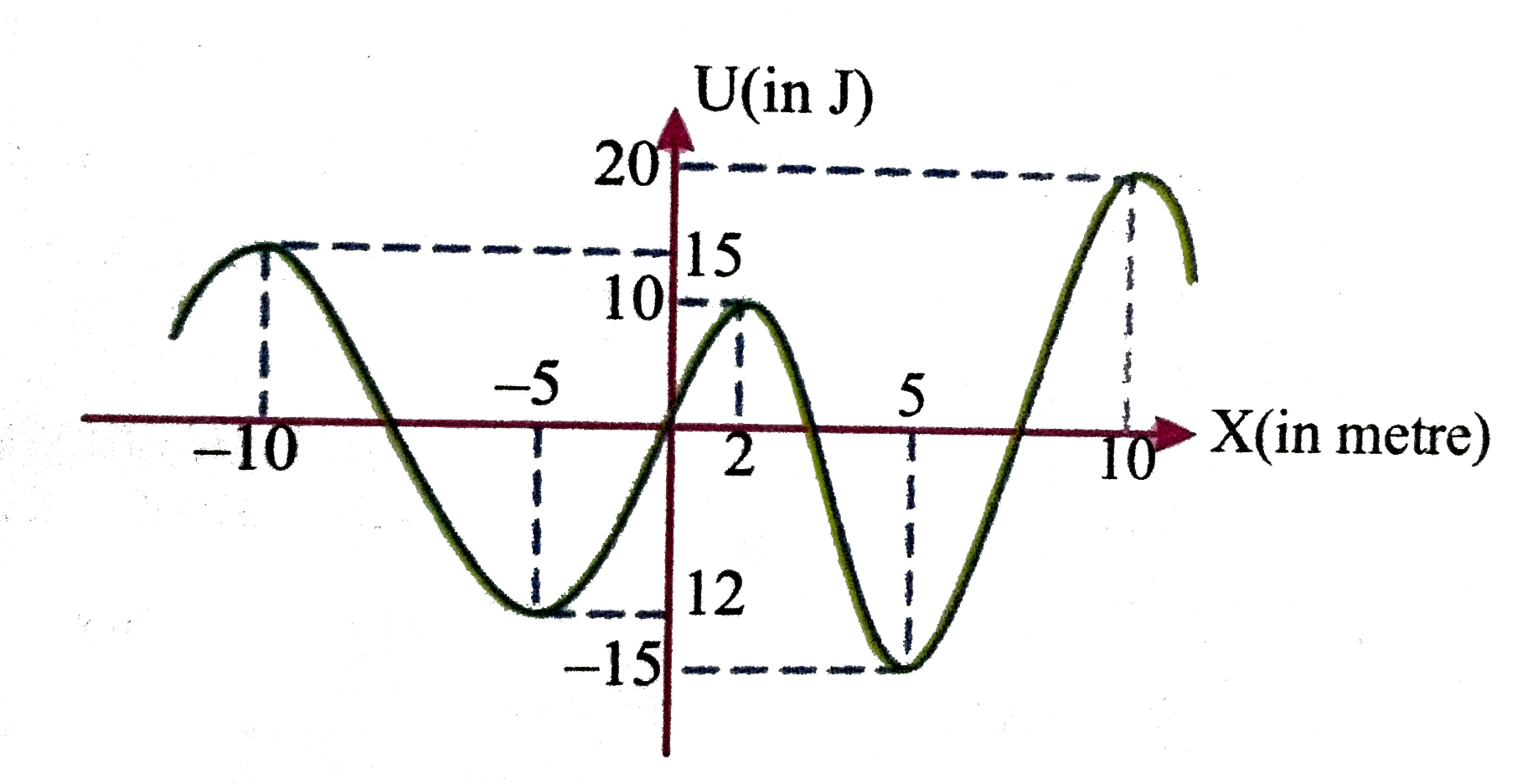
`x = - 5m` and `x = 10 m` position of the particle are respectively of

A block of mass 10 kg is put gently on a belt-conveyor system of infinite length at t = 0, which is moving with constant speed `20 m//sec` towards right at all time.

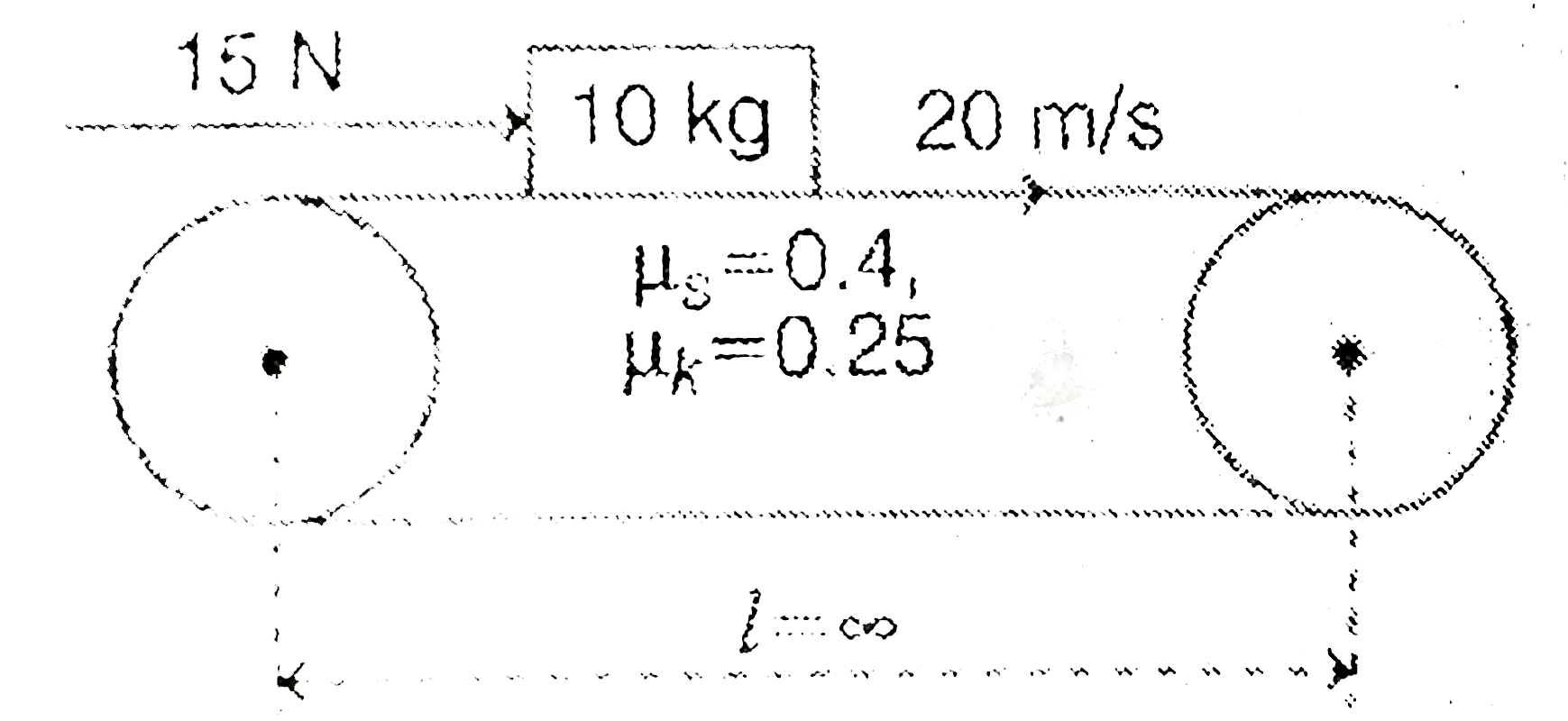
A constant force of magnitude 15 N is applied on the block continuously during its motion.
The nature of friction acting on the block of mass 10 kg during its motion is

A block of mass 10 kg is put gently on a belt-conveyor system of infinite length at t = 0, which is moving with constant speed `20 m//sec` towards right at all time.

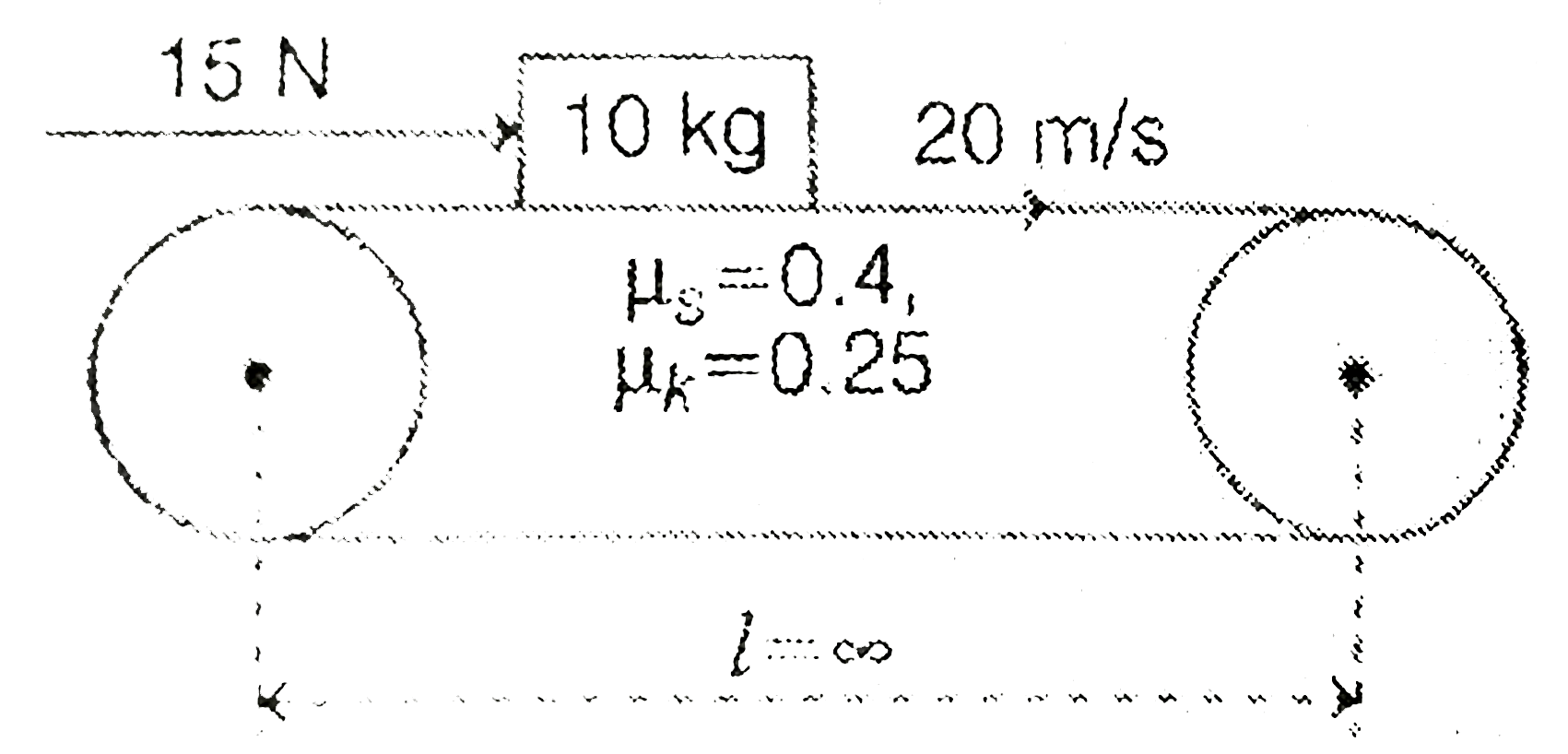
A constant force of magnitude 15 N is applied on the block continuously during its motion.
Work done by the kinetic friction on the block of mass 10 kg is

A block of mass 10 kg is put gently on a belt-conveyor system of infinite length at t = 0, which is moving with constant speed `20 m//sec` towards right at all time.

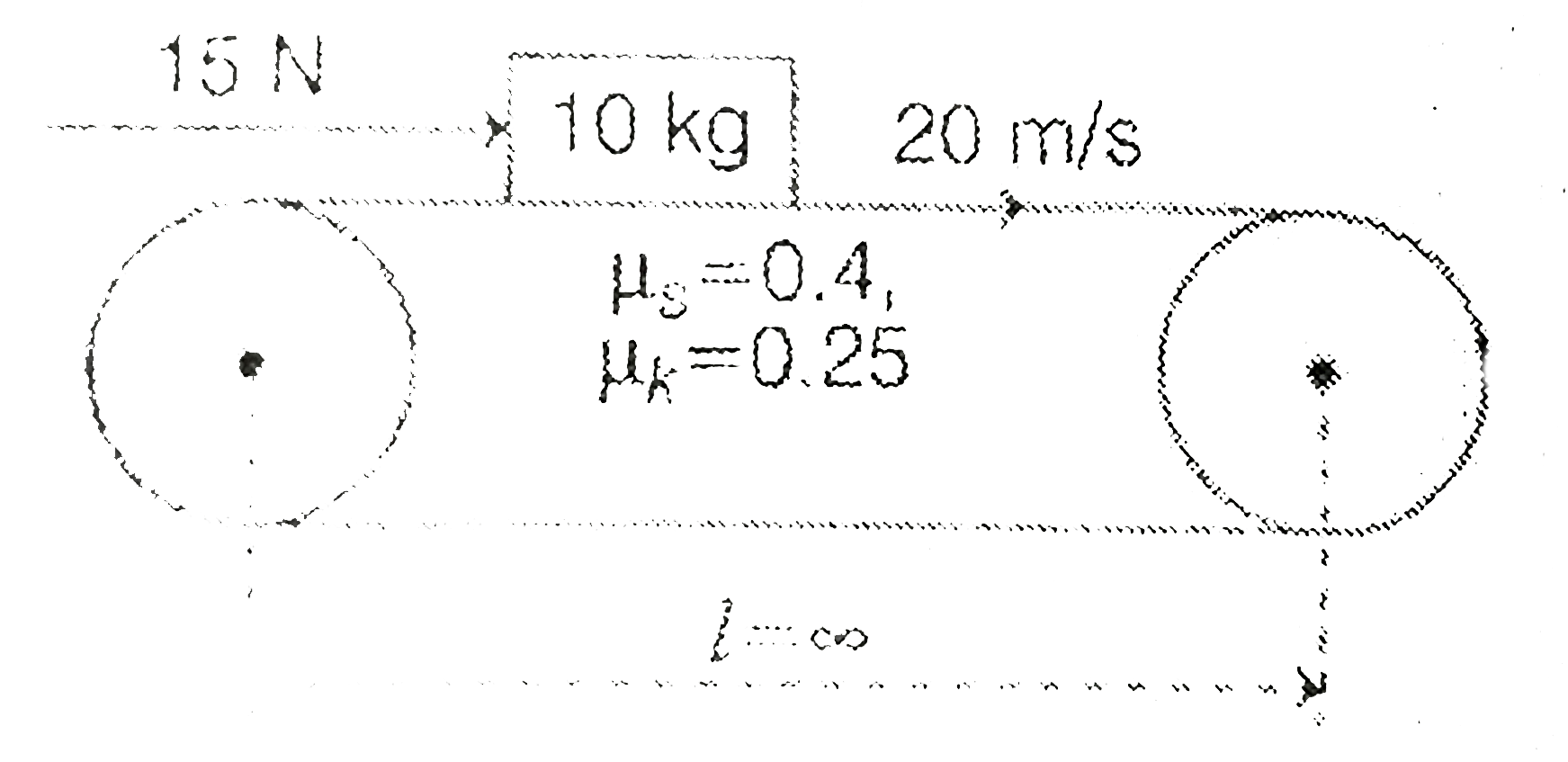
A constant force of magnitude 15 N is applied on the block continuously during its motion.
The magnitude of acceleration of the block of mass 10 kg at t = 6s is