Complete Solutions to A Only One Option is Correct of chapter WORK, POWER AND ENERGY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, POWER AND ENERGY |
| DC PANDEY MASTER PROBLEM PACKAGE | A Only One Option is Correct |
| Number Of Questions | 42 |
| Academic Year | 2023-24 |
Kinetic energy of a particle moving in a straight line varies with time `t` as `K = 4t^(2)`. The force acting on the particle
View SolutionA particle of mass `2 kg` starts moving in a straight line with an initial velocity of `2 m//s` at a constant acceleration of `2 m//s^(2)`. Then rate of change of kinetic energy.
View SolutionA particle moves move on the rough horizontal ground with some initial velocity `V_(0)`. If `(3)/(4)` of its kinetic enegry lost due to friction in time `t_(0)`. The coefficient of friction between the particle and the ground is.
View SolutionTwo particles `1` and `2` are allowed to descend on the two frictionless chord `OA` and `OB` of a vertical circle, at the same instant from point `O`. The ratio of the velocities of the particles `1` and `2` respectively, when they reach on the circumference will be (OB is the diameter).
View SolutionA body is displaced from `(0,0)` to `(1 m, 1m)` along the path `x = y` by a force `F=(x^(2) hatj + y hati)N`. The work done by this force will be
View SolutionA self-propelled vehicle of mass m, whose engine delivers a constant power P, has an acceleration `a = (P//mv)`. (Assume that there is no friction). In order to increase its velocity from `v_(1)` to `v_(2)`, the distan~e it has to travel will be:
View SolutionA body is moved from rest along a straight line by a machine delivering constant power. The ratio of displacement and velocity `(s//v)` varies with time `t` as
View SolutionA force`F = (2hat(i)+5hat(j)+hat(k))N` is acting on a particle. The particle is first displacement from (0, 0, 0) to (2m, 2m, 0) along the path x = y and then from (2m, 2m, 0) to (2m, 2m, 2m) along the path x = 2m, y = 2 m. The total work done in the complete path is
View SolutionA vertical spring of force cosntant `100 N//m` is attached with a hanging mass of 10 kg. Now an external force is applied on the mass so that the spring is stretched by additional 2m. The work done by the force F is `(g = 10 m//s^(2))`
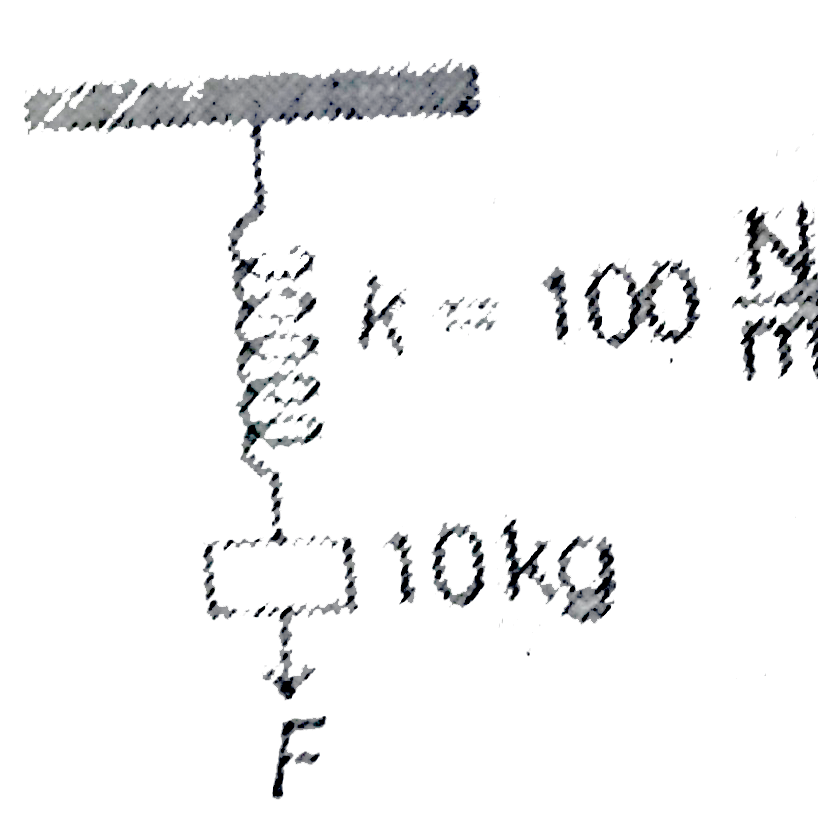
View SolutionA partical is realeased from the top of two inclined rought surface of height `h` each. The angle of inclination of the two planes are `30^(@)` and `60^(@)` respectively. All other factors (e.g. coefficient of friction , mass of the block etc) are same in both the cases. Let `K_(1) and K_(2)` be the kinetic energy of the partical at the bottom of the plane in two cases. Then
View SolutionSystem shown in figure is released from rest . Pulley and spring is mass less and friction is absent everywhere. The speed of `5 kg` block when `2 kg` block leaves the constant of with ground is (force constant of spring `k = 40 N//m and g = 10 m//s^(2))`

View SolutionForce acting on a particale is `(2hat(i)+3hat(j))N`. Work done by this force is zero, when the particle is moved on the line `3y+kx=5`. Here value of k is `(`Work done `W=vec(F).vec(d))`
View SolutionAn object of mass `m` slides down a hill of arbitrary shape and after travelling a certain horizontal path stops because of friction. The total vertical height descended is `h`. The friction coefficient is different for different segments for the entire path but is independent of the velocity and direction of motion. The work that a tangerial force must perform to return the object to its initial position along the same path is
View SolutionA block of mass m slides down a rough inclined plane of inclination `theta` with horizontal with zero initial velocity. The coefficient of friction between the block and the plane is `mu` with `theta gt tan^(-1)(mu)`. Rate of work done by the force of friction at time t is
A.`mumg^(2)tsintheta` B.`mg^(2)t(sintheta-mucostheta)` C.`mumg^(2)tcostheta(sintheta-mucostheta)` D.`mumg^(2)tcostheta`
View SolutionA `1.5-kg` block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of x-axis is applied to the block. The force is given by `vecF=(4-x^2)veciN`, where x is in meter and the initial position of the block is `x=0`.
The maximum kinetic energy of the block between `x=0` and `x=2.0m` is
A.2.33 J B.8.67 J C.5.33 J D.6.67 J
View SolutionIn the above problem, the maximum positive displacement x is
View SolutionA block of mass 1 kg is attached to one end of a spring of force constant k = 20 N/m. The other end of the spring is attached to a fixed rigid support. This spring block system is made to oscillate on a rough horizontal surface `(mu = 0.04)`. The initial displacement of the block from the equilibrium position is a = 30 cm. How many times the block passes from the mean position before coming to rest ? `(g = 10 m//s^(2))`
View SolutionTwo block of masses `m_(1)` and `m_(2)` connected by a light spring rest on a horizontal plane. The coefficient of friction between the block and the surface is equal to `mu`. What minimum constant force has to be applied in the horizontal direction to the block of mass `m_(1)` in order to shift the other block?
View SolutionA block of mass m is attached with a massless spring of force constant k. The block is placed over a rough inclined surface for which the coefficient of friction is `mu=(3)/(4)`. The minimum value of M required to move the block up the plane is (Neglect mass of string, mass of pulley and friction in pulley)

View SolutionThe potential energy of a particle of mass m is given by `U=(1)/(2)kx^(2)` for `x lt 0` and U = 0 for `x ge 0`. If total mechanical energy of the particle is E. Then its speed at `x = sqrt((2E)/(k))` is
View SolutionA body of mass 2 kg is moved from a point A to a point B by an external agent in a conservative force field. If the velocity of the body at the points A and B are `5 m//s` and `3 m//s` respectively and the work done by the external agent is - 10 J, then the change in potential energy between point A and B is
View SolutionA block of mass m = 0.1 kg is released from a height of 4m on a curved smooth surface. On the horizontal surface, path AB is smooth and path BC offers coefficient of friction `mu` = 01. If the impact of block with the vertical wall at C be elastic, the total distance covered by the block on the horizontal surface before coming to rest will be (take `g = 10 m//s^(2)`)

View SolutionA system consists of two cubes of mass `m_(1)`, and `m_(2)` respectively connected by a spring of force constant k. force (F) that should be applied to the upper cube for which the lower one just lifts after the force is removed, is
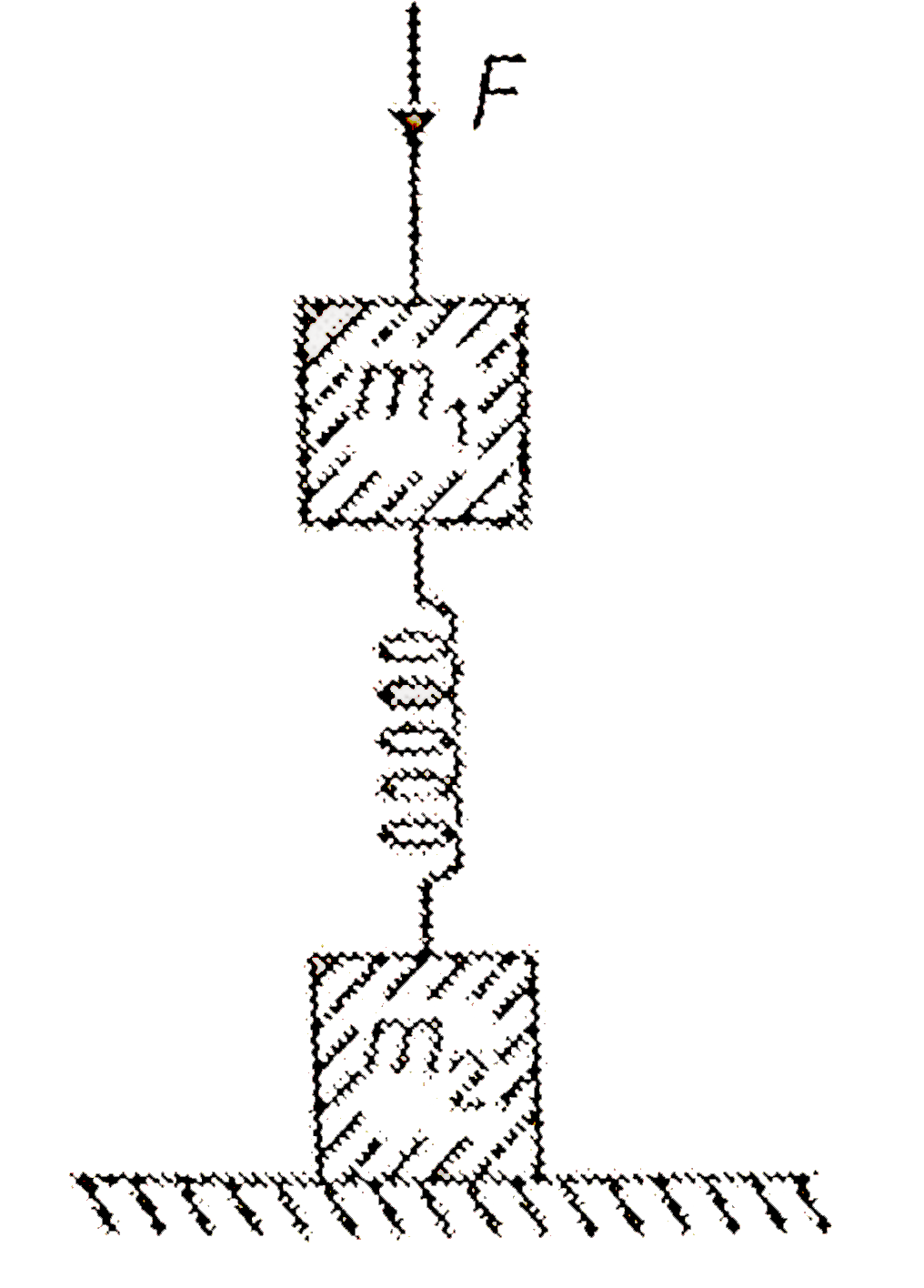
View SolutionA block mass `m = 2 kg` is moving with velocity`v_(0)` towards a mass less unstretched spring of the force constant `k = 10 N//m`. Coefficient of friction between the block and the ground is `mu = 0.2`. Find the maximum value of `v_(0)` so that after pressing the spring the block does not return back but stops there permanently.

View SolutionIn a projectile motion, if we plot a graph between power of the force acting on the projectile and time, then it would be like
View SolutionPotential energy of a particle moving along x-axis under the action of only conservative force is given as `U=10+4cos(4pi x)`. Here, U is in Joule and x in metres. Total mechanial energy of the particle is 16 J. Choose the correct option.
View SolutionAcceleration of a particle moving in `x-y` plane varies with time t as. `vec(a) = (ti + 3t^(2)j)`.
Here a is in `m//s^(2)` and t in sec. At time `t = 0` particle is at rest origin. Mass of the particles is `1 kg`. Find the net work done on the particle in first `2 sec`.
View SolutionA small mass slides down an inclined plane of inclination `theta` with the horizontal. The co-efficient of friction is `mu=mu_(0)` x where x is the distance through which the mass slides down and `mu_(0)` a constant. Then, the distance covered by the mass before it stops is
View SolutionFigure, a block slides along a track from one level to a higher level by moving through an intermediate valley. The track is friction less until the block reaches the higher
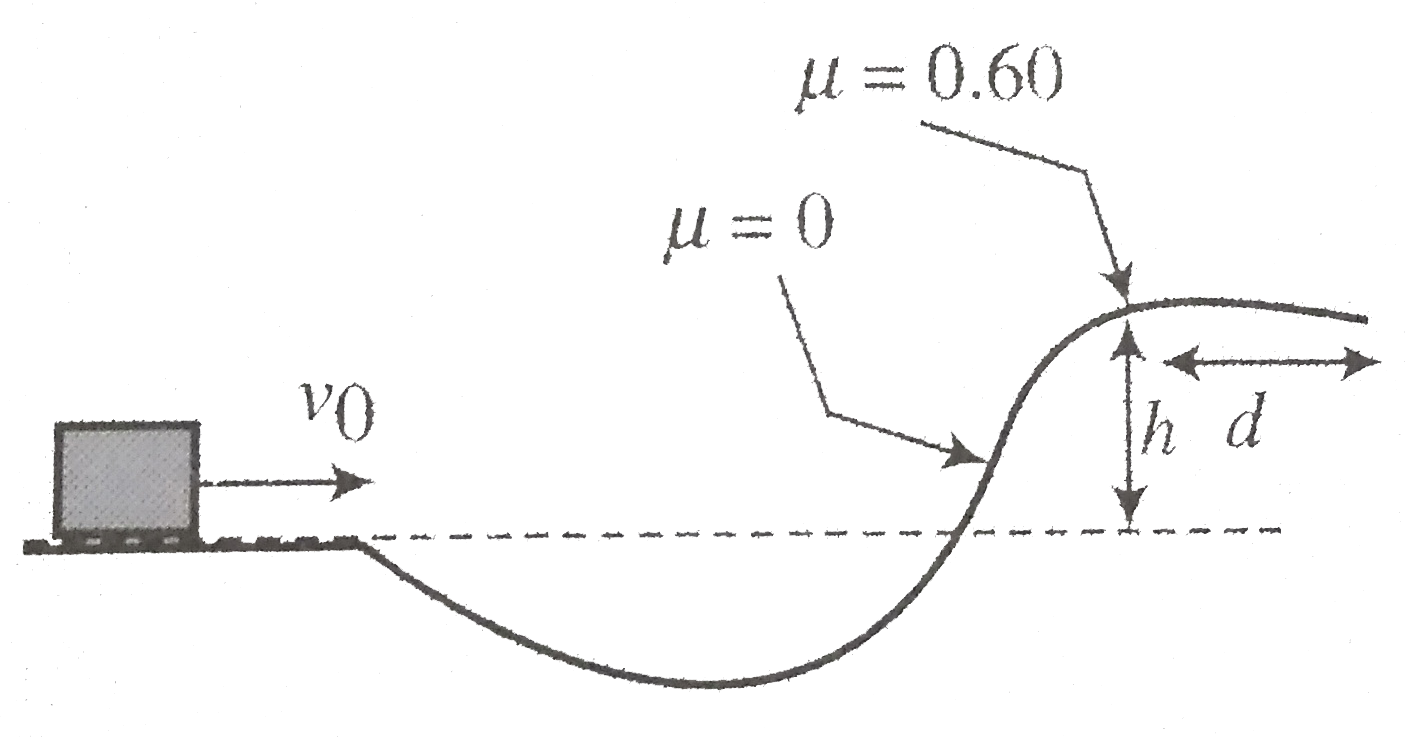 level. Then there is friction force which stops the block at a distance d. The block's initial speed `v_0` is `6.0ms^-1`, the height difference `h` is `1.1m`, and the coefficient of kinetic friction `mu` is `0.60`. Find `d`.
level. Then there is friction force which stops the block at a distance d. The block's initial speed `v_0` is `6.0ms^-1`, the height difference `h` is `1.1m`, and the coefficient of kinetic friction `mu` is `0.60`. Find `d`.
View SolutionIn the figure the variation of components of acceleration of a particle of mass is `1 kg` is shown w.r.t. time. The initial velocity of the particle is `vec u=(- 3i + 4j) m//s`. The total work done by the resultant force on the particle in time from `t = 0` to `t = 4` seconds is :
 .
.
View SolutionA block attached to a spring, pulled by a constant horizontal force, is kept on a smooth surface as shown in figure. Initially, the spring is in the natural length state. Then the maximum positive work that the applied force F can do is (give that string does not break)

View Solution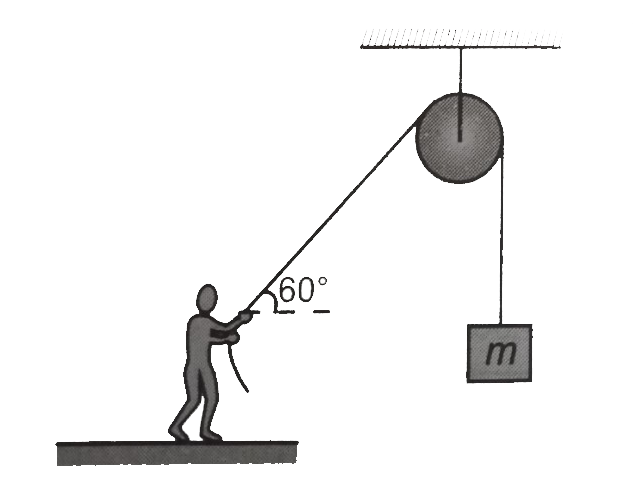
A man is supplying a constant power of 500`(J)/(s)` to a massless string by pulling it at a constant speed of `10(m)/(s)` an shown. It is known that kinetic energy of the block is increasing at a rate of `100(J)/(s)`. Then the mass of the block is:\
View SolutionIn the figure shown all the surfaces are frictionless and mass of block `m=1kg`, block and wedge are held initially at rest, now wedge is given a horizontal acceleration of `10 m//s^(2)` by applying a force on the wedge so that the block does not slip on the wedge, the work done by normal force in ground frame on the block in `sqrt(3) sec` is
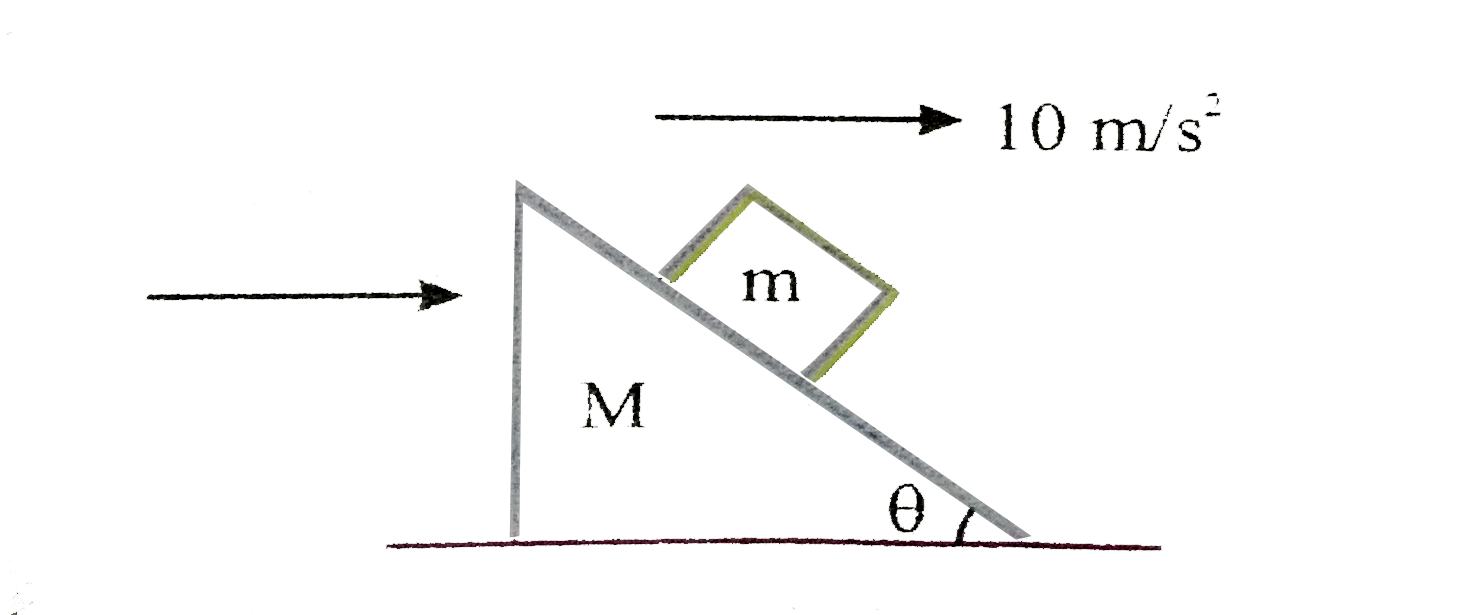 .
.
View SolutionAs shown in the figure a block of mass 'm' is placed on a smooth wedge moving with constant acceleration such that block does not move with respect to the wedge. Find work done by the net force on the block in time t. (Initial speed is 0)
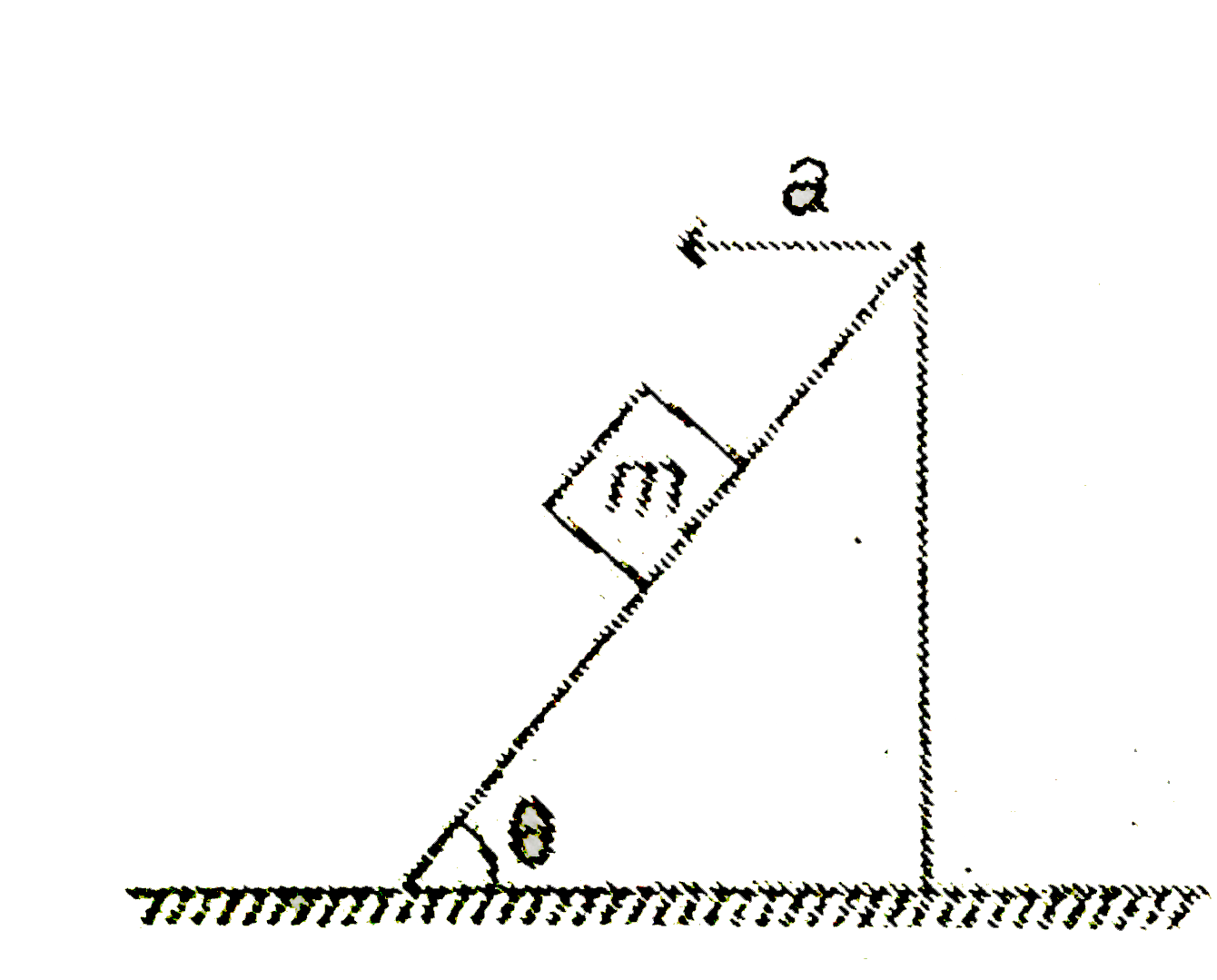
View SolutionA body is moving up an inclined plane of angle `theta` with an initial kinetic energy E. The coefficient of friction between the plane and body is `mu`. The work done against friction before the body comes to rest is
View SolutionThree components of a force acting on a particle are varying according to the graphs as shown. To reach at point B(8, 20, 0)m from point A(0, 5, 12)m the particle moves on paths parallel to x-axis then y-axis and then z-axis, then work done by this force is:
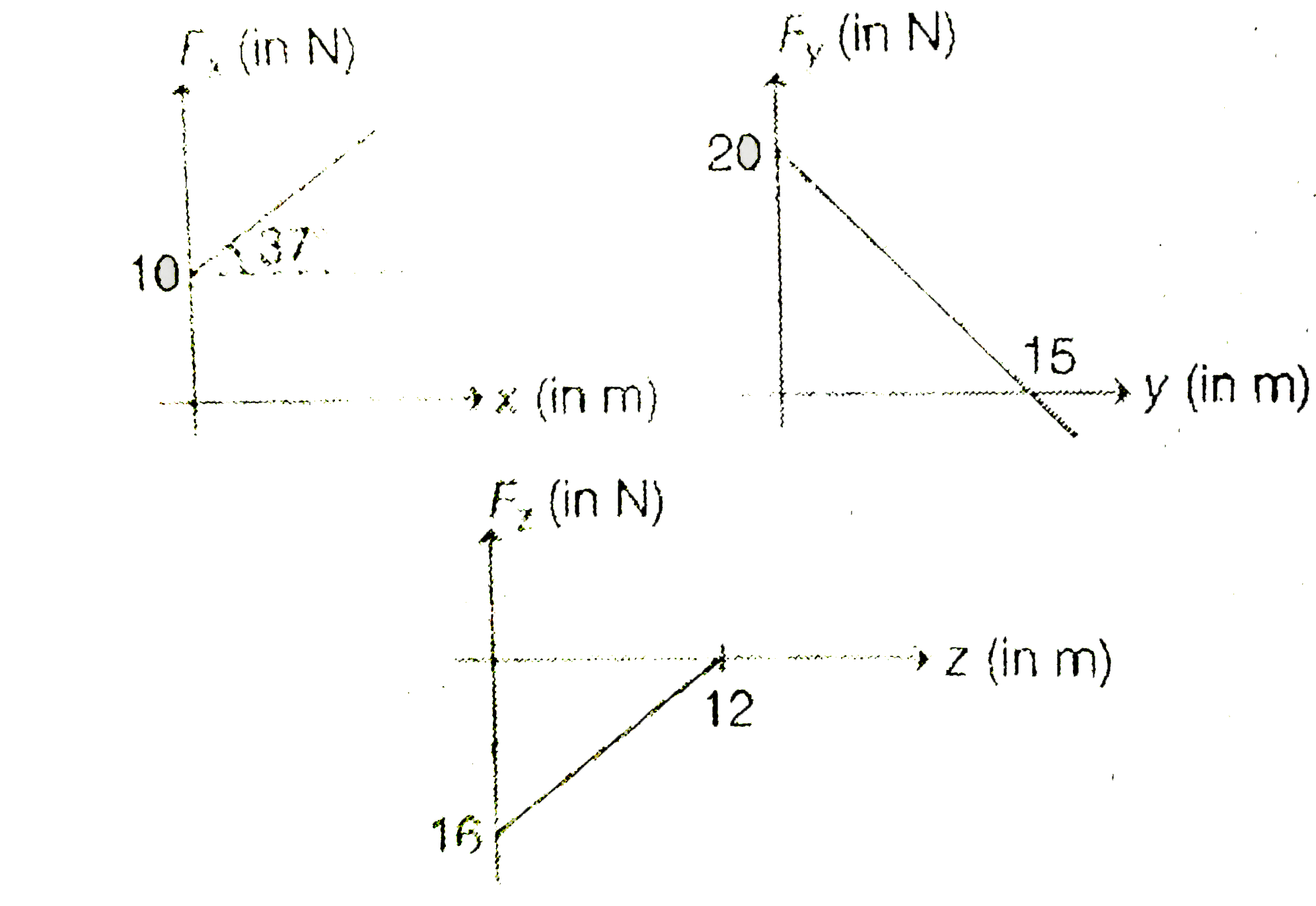
View SolutionA floor-mat of mass M made up of extensible material, is rolled along its length so as to form a cylinder of radius R and kept on a rough horizontal surface. If the mat is now unrolled, without sliding, to a radius `(R )/(2)`, the decrease in potential energy is
View SolutionA block of mass m is attached to a frame by a light spring of force constant k. The frame and block are initially at rest with `x = x_(0)`, the natural length of the spring. If the frame is given a constant horizontal accelration `a_(0)` towards left, determine the maximum velocity of the block relative to the frame (block is free to move inside frame). Ignore any friction.
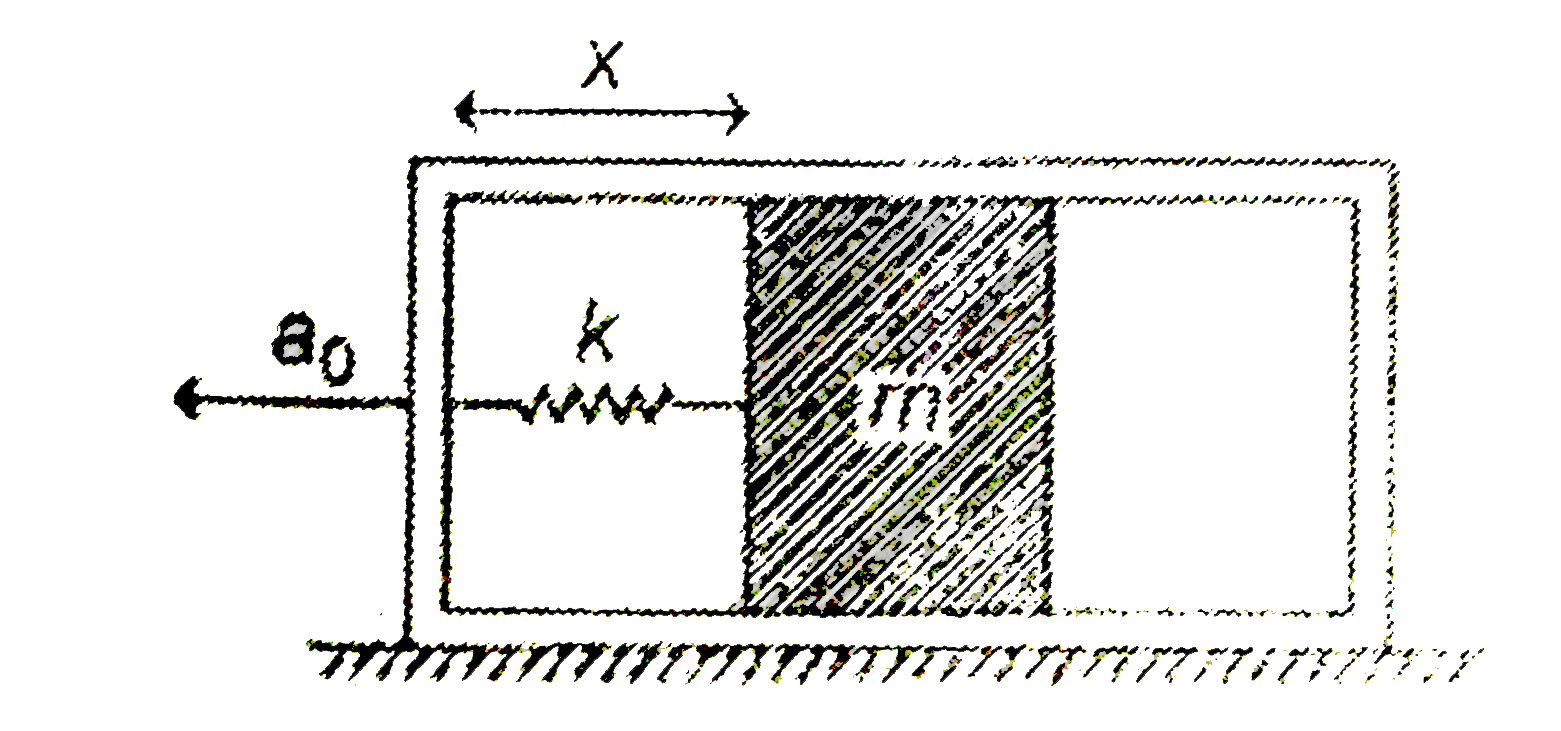
View SolutionFigure shows two small blocks placed on smooth horizontal surface. They start moving from the same line with forces 2F and F respectively acting on the blocks. Their momenta and kinetic energies at the instant of crossing the finishing line as shown in figure are `P_(A), P_(B)` and `K_(A), K_(B)`. Then choose the correct option.
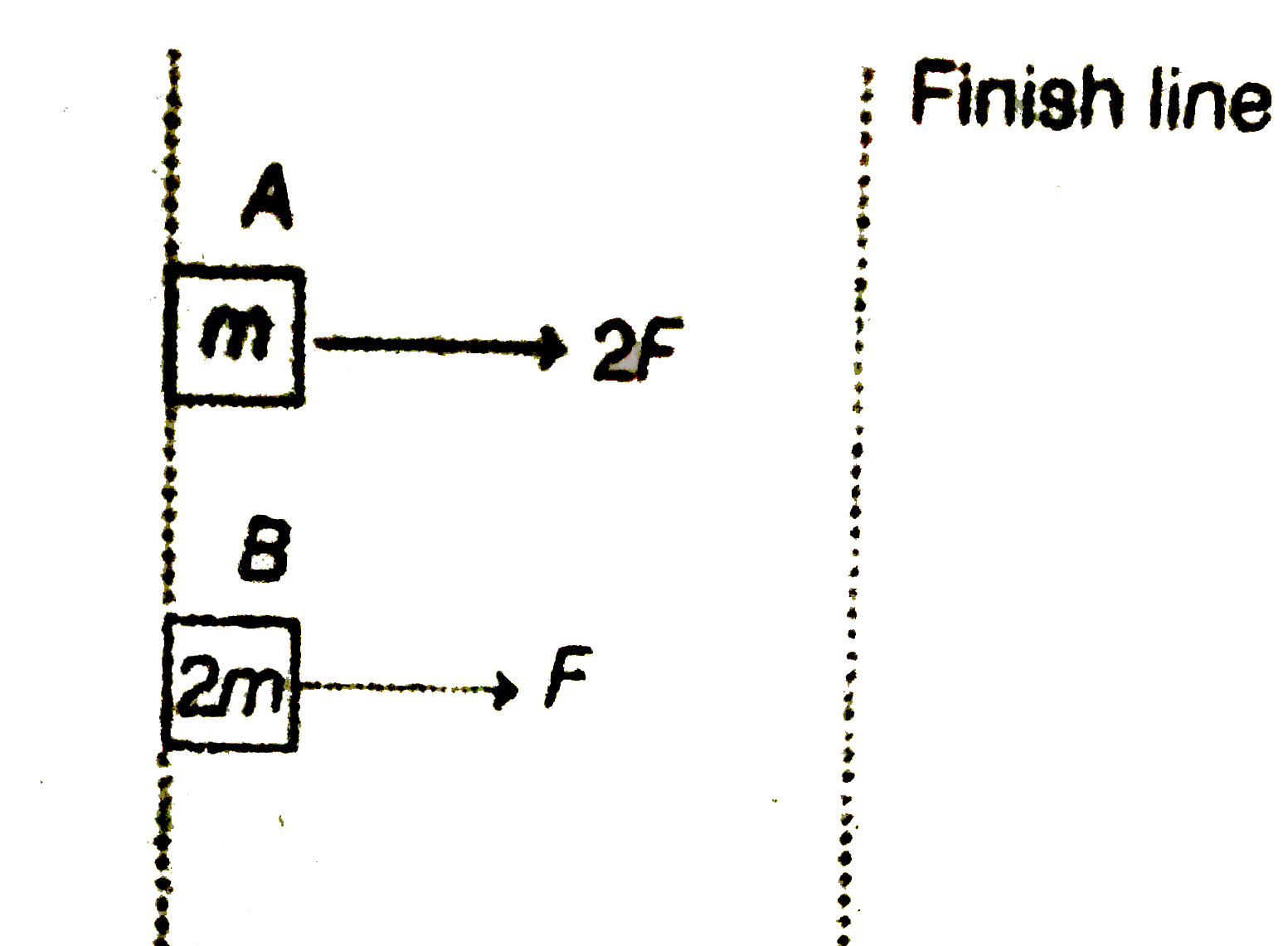
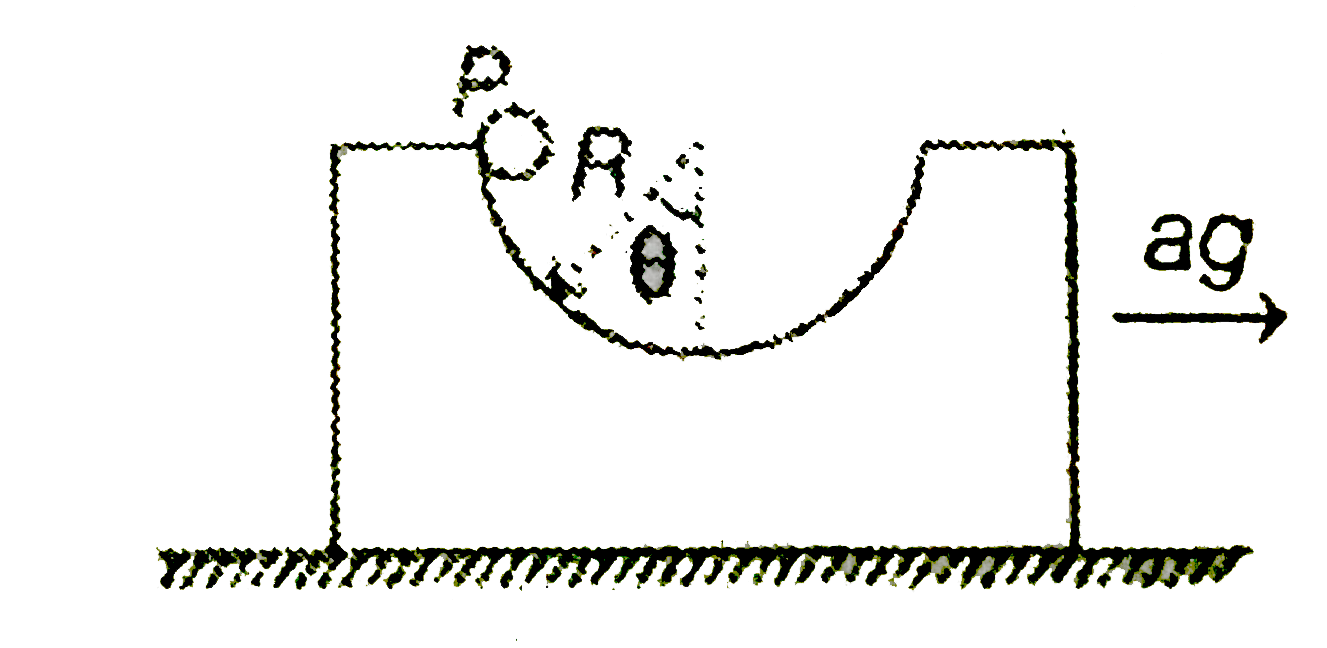
View SolutionInside a smooth hemispherical cavity, a particle P can slide freely. The block having this cavity is moving with constant acceleration a = g (where g is acceleration due to gravity). The particle is released from the state of rest from the topmost position of the surface of the cavity as shown. The angle `theta` with the vertical, when the particle will have maximum velocity with respect to the block is
View SolutionA block of mass M slides along a horizontal table with speed `v_(0)`. At `x=0`, it hits a spring with spring constant k and begins to experience a friction force. The coefficient of friction is variable and is given by `mu=bx`, where b is a positive constant. Find the loss in mechanical energy when the block has first come momentarily to rest.
 .
.
View SolutionA ball of mass m is thrown upward with a velocity `upsilon`. If air exerts an average resisting force F, the velocity with which the ball returns to the thrower is
View Solution
A Only One Option is Correct questions and complete solutions for chapter WORK, POWER AND ENERGY of DC PANDEY ENGLISH of Class 11