Complete Solutions to Only One Option is Correct of chapter WORK, POWER AND ENERGY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, POWER AND ENERGY |
| DC PANDEY MASTER PROBLEM PACKAGE | Only One Option is Correct |
| Number Of Questions | 39 |
| Academic Year | 2023-24 |
A block of mass m is suspended by a light thread from an elevator. The elevator is accelerating upward with uniform acceleration a. The work done by tension on the block during t seconds is (u = 0)
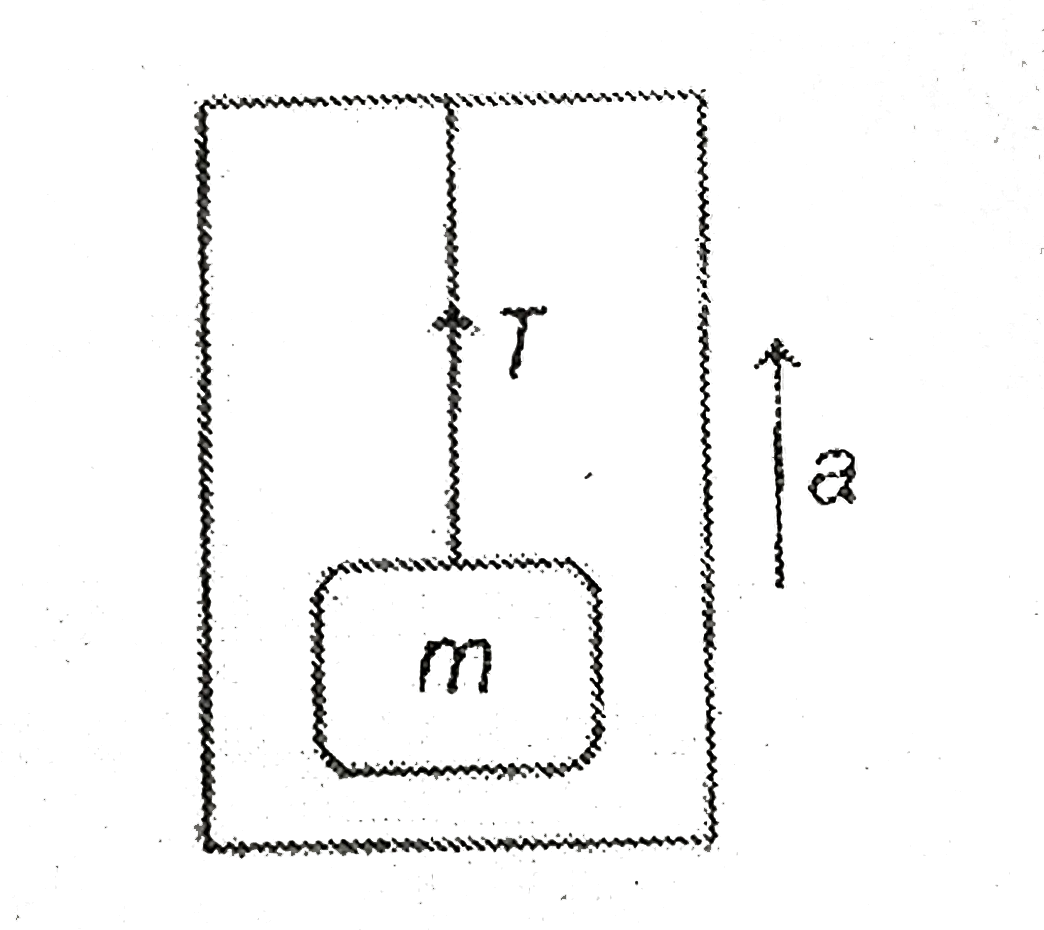
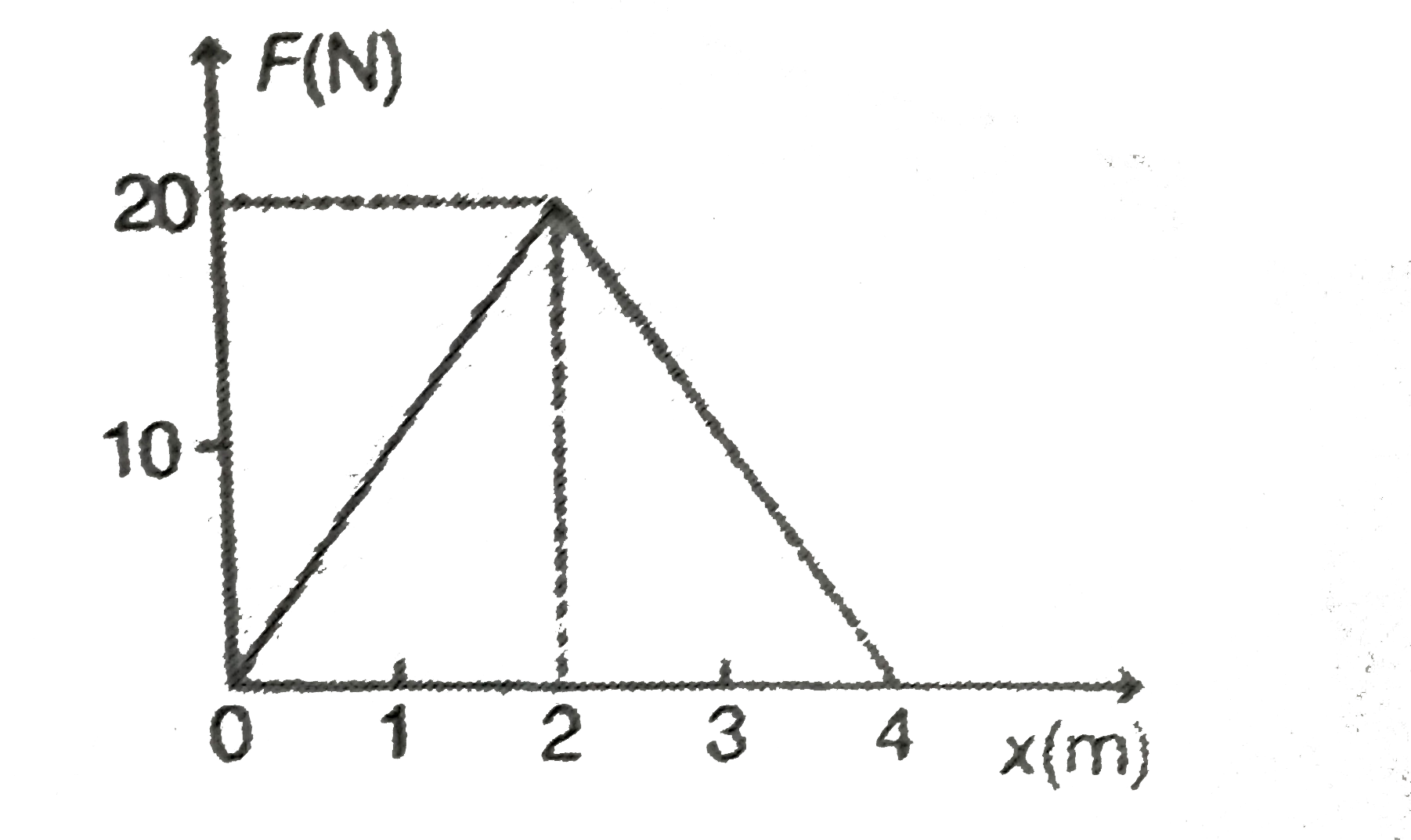
View SolutionThe graph between the resistance force F acting on a body and the distance covered by the body is shown in the figure. The mass of the body is 25kg and initial velocity is `2 m//s^(2)`. When the distance covered by the body is 4m, its kinetic energy would be
View SolutionA block weighing 10 N travels down a smooth curved track AB joined to a rough horizontal surface (figure). The rough surface has a friction coefficient of 0.20 with the block. If the block is released from rest on the track from a point 1.0 m above the horizontal surface, the distance it will move on the rough surface is

View Solution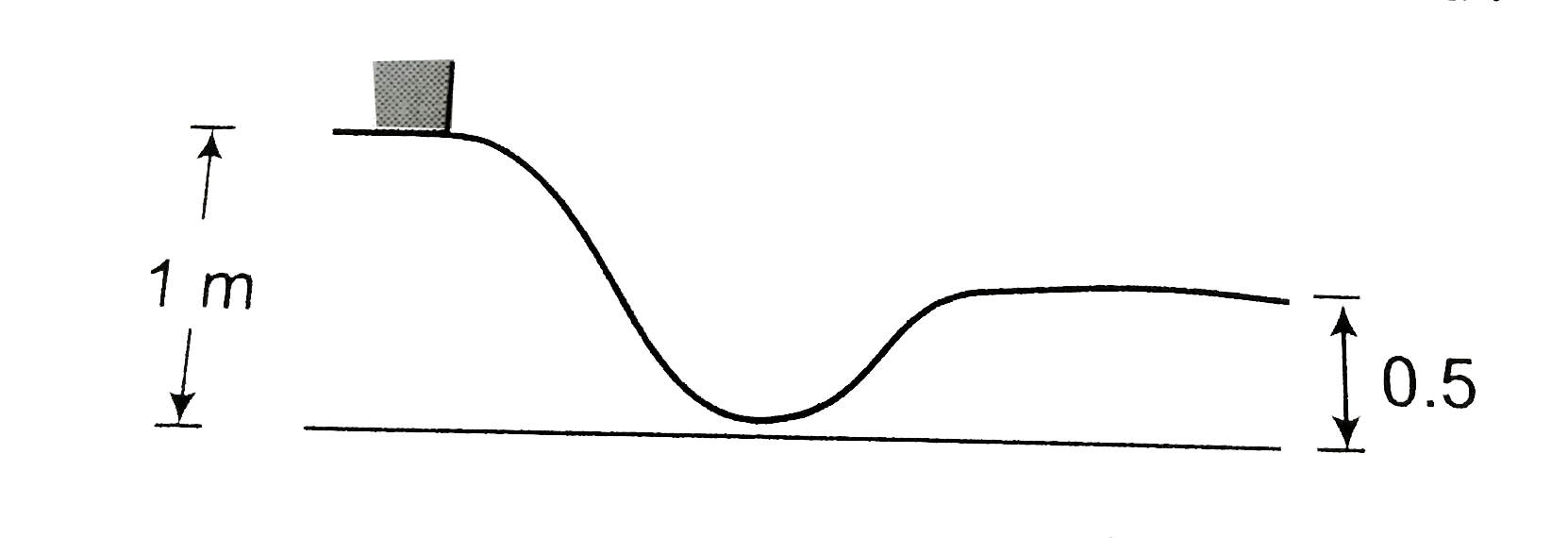
The figure shown a particle sliding on a frictionless track, which teminates in a straight horizontal section. If the particle starts slipping from the point `A`, how far away from the track will the particle hit the ground?
View SolutionA block of mass m is attached to two unstretched springs of springs constant `k_(1)` and `k_(2)` as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.

View SolutionA body of mass m dropped from a certain height strikes a light vertical fixed spring of stifness k. the height of its fall before touching the spring the if the maximum compression of the spring the equal to `(3 mg)/k` is
View SolutionPotential energy `v//s` position curve for one dimensional conservative field is shown. Force at A and B is respectively.

View SolutionForce acting on a block moving along x-axis is given by
`F = - ((4)/(x^(2)+2))N`
The block is displaced from `x = - 2m` to `x = + 4m`, the work done will be
View SolutionA block of mass 50 kg is projected horizontal on a rough horizontal floor. The coefficient of friction between the block and the floor is 0.1. The block strikes a light spring of stiffness `k = 100 N//m` with a velocity `2 m//s`, the maximum compression of the spring is

View SolutionA block of mass 250g is kept on a vertical spring of spring constant 100N/m fixed from below. The spring is now compressed to have a length 10cm shorter than its natural length and the system is released from this position. How high does the block rise? take `g=10 m/s^2`.
View SolutionThe potential energy of the system is represented in the first figure. The force acting on the system will be represented by
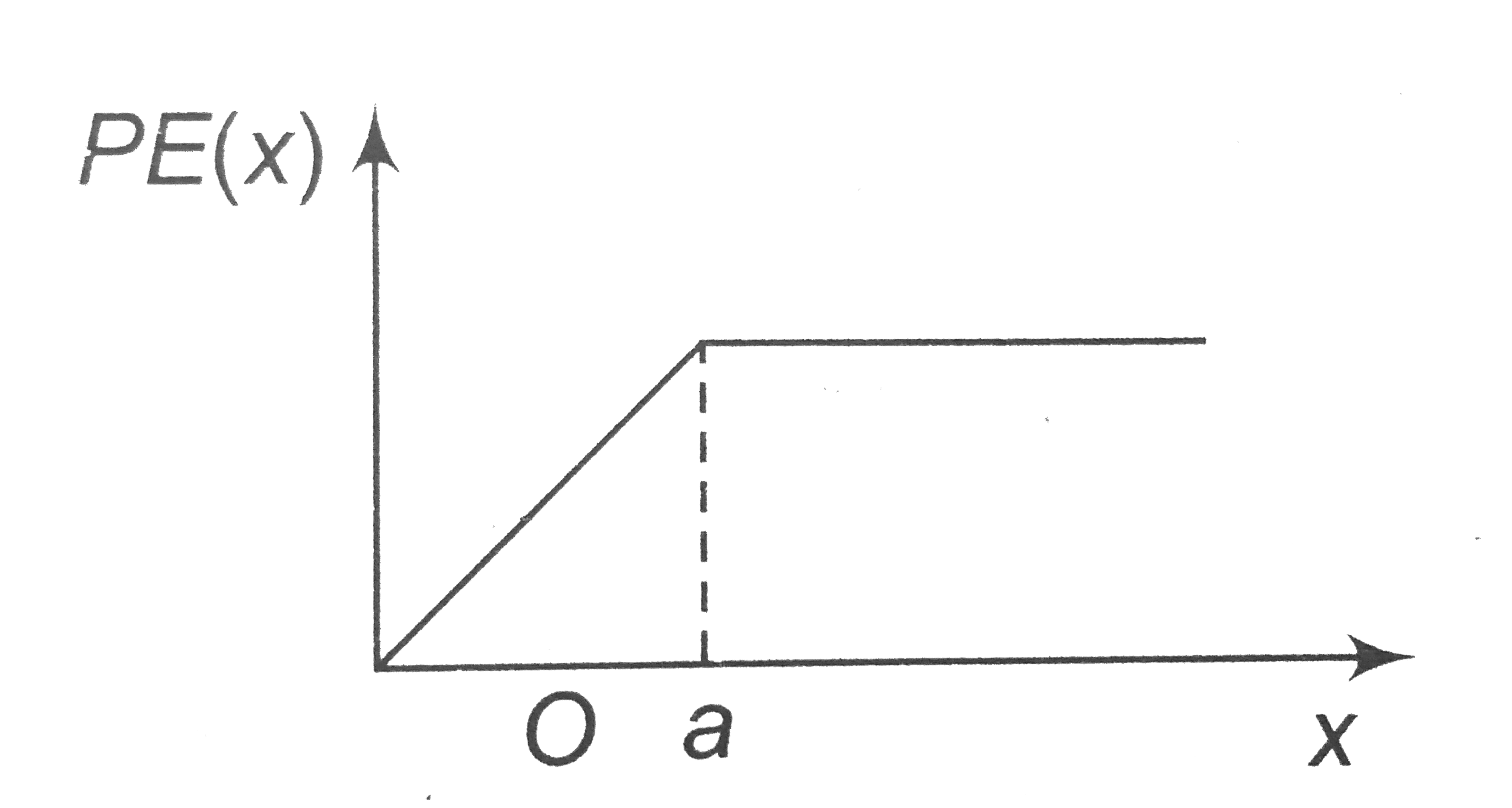
View Solution`F = 2x^(2)-3x-2`. Choose correct option.
View SolutionA block of mass m is hung vertically from an elastic thread of force constant `mg//a`. Initially the thread was at its natural length and the block is allowed to fall freely. Kinetic energy of the block when it passes through the equilibrium position will be
View SolutionA block of mass m tied to a string is lowered by a distance d, at a constant acceleration of `g//3`. The work done by the string is
View SolutionFrom the fixed pulley, masses 2kg, 1kg and 3kg are suspended as shown in the figure. Find the extension in the spring if `k=100 N//m`. (Neglect oscillations due to spring)
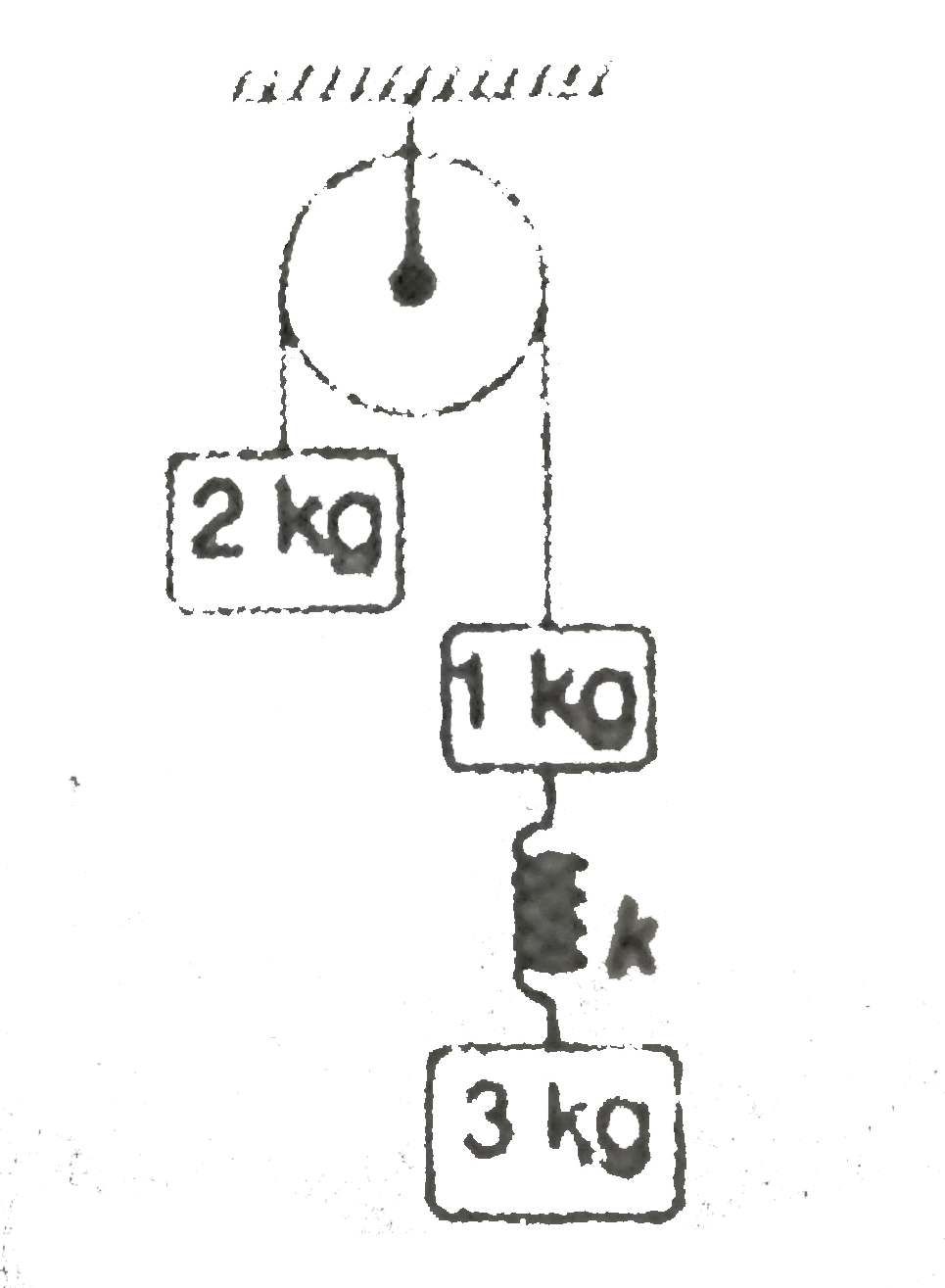
View SolutionA rope of length `l` and mass 'm' is connected to a chain of length `l` and mass `2 m` and hung vertically as shown. What is the change in graviational potential energy if the system is inverted and hung from same point.
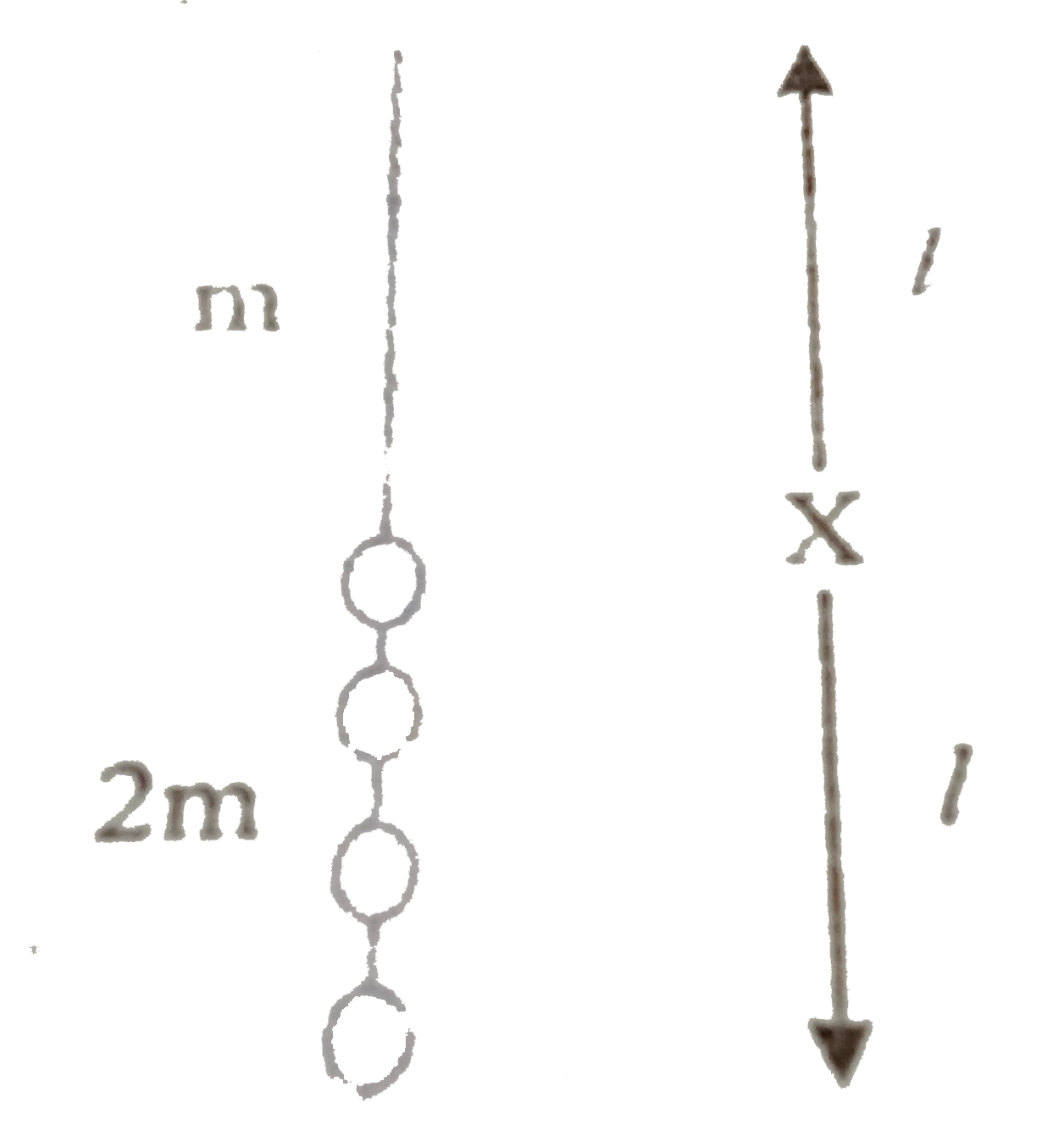 .
.
View Solutionv-t graph of an object of mass 1 kg is shown.Select the wrong statement-

View SolutionA `15 gm` ball is shot from a spring whose spring has a force constant of `600 N//m`. The spring is compressed by `5 cm`. The greatest possible horizontal range of the ball for this compression is
View SolutionPower supplied to a mass `2 kg` varies with time as `P = (3t^(2))/(2)` watt. Here `t` is in second . If velocity of particle at `t = 0 is v = 0`, the velocity of particle at time `t = 2s` will be:
View SolutionA ball is released from the top of a tower. The ratio of work done by force of gravity in 1st second, 2nd second and 3rd second of the motion of ball is
View SolutionA particle is released from height `H`. At certain height from the ground its kinetic energy is twice its gravitational potential energy. Find the height and speed of particle at that height.
View SolutionA body is moved along a straight line by a machine delivering constant power . The distance moved by the body is time `t` is proptional to
View SolutionThe displacement of a body of mass `2 kg` varies with time `t` as `S = t^(2) + 2t`, where `S` is in seconds. The work done by all the forces acting on the body during the time interval `t = 2s` to `t = 4s` is
View SolutionThe work done by a force `vec(F)=(-6x^(3)hat(i))` N in displacing a particle from x = 4m to x = - 2m is
View SolutionThe velocity-time graph of a particle moving in a straight line is shown in figure. The mass of the particle is `2kg`. Work done by all the forces acting on the particle in time interval between `t=0` to `t=10s` is

View SolutionThe force acting on a body moving along x -axis varies with the position of the particle as shown in the fig. The body is in stable equilibrium at.
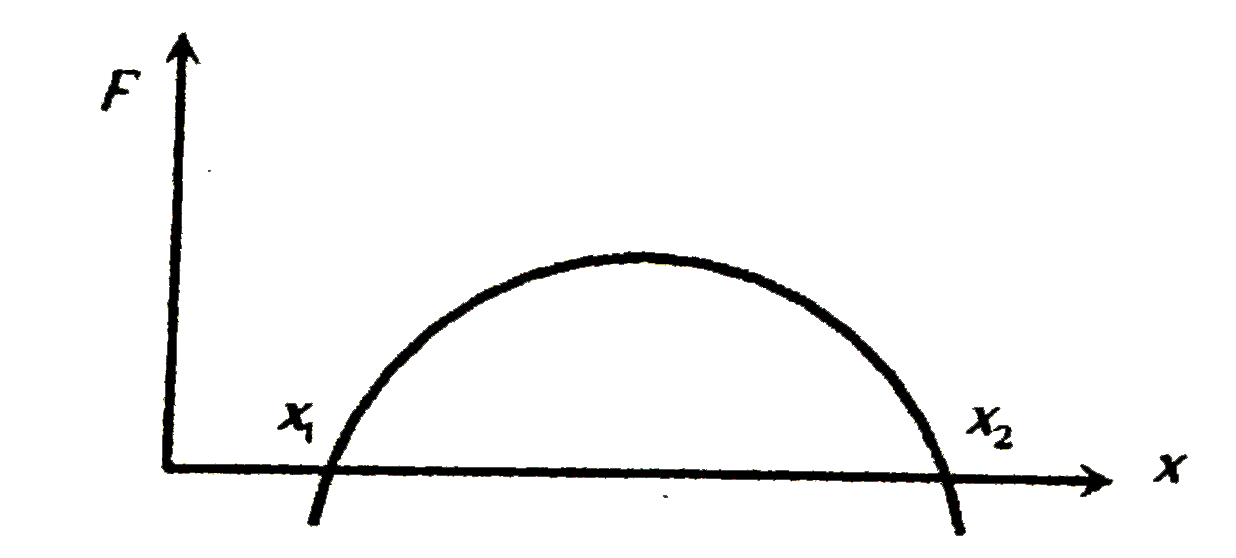
View Solution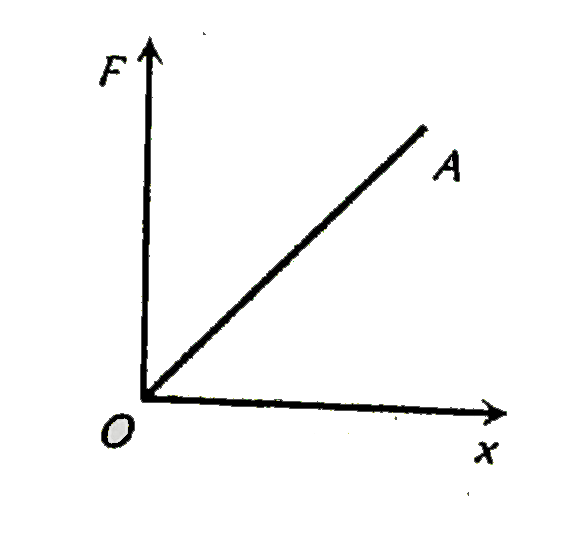
The force required to stretch a spring varies with the distance a shown in the figure. If the experiment is performed with the above spring of half length, the line OA will
View SolutionA force `F` acting on a body depends on its displacement `S` as `FpropS^(-1//3)` . The power delivered by `F` will depend on displacement as
View SolutionA man throws the bricks to a height of 12 m where they reach with a speed of `12 m//s`. If he throws the bricks such that they just reach that height, what percentage of energy will be saved? `(g = 9.8 m//s^(2))`
View SolutionThe ratio of momentum and kinetic energy of particle is inversely proportional to the time. Then, this is the case of a
View SolutionA block of mass m is pulled by a constant powert `P` placed on a rough horizontal plane. The friction coefficient the block and surface is `mu`. The maximum velocity of the block is.
View SolutionAn object of mass `m` is allowed to fall from rest along a rough inclined plane. The speed of the object on reaching the bottom of the plane is proportional to:
View SolutionA particle is moved from (0, 0) to (a, a) under a force a `F=(3hat(i)+4hat(j))` from two paths. Path 1 is OP and path 2 is OPQ. Let `W_(1)` and `W_(2)` be the work done by this force in these two paths. Then,
View SolutionA particle of mass `0.5 kg` is displaced from position `vec r_(1)(2,3,1)` to`vec r_(2)(4,3,2)` by applying a force of magnitude `30 N` which is acting along `(hati + hatj + hatk)`. The work done by the force is
View SolutionA uniform flexible chain of mass m and length 2l hangs in equilibrium over a smooth horizontal pin of negligible diameter. One end of the chain is given a small vertical displacement so that the chain slips over the pin. The speed of chain when it leaves the pin is
View SolutionA block is released from the top of a smooth inclined plane of inclination `theta` as shown in figure. Let `upsilon` be the speed of the particle after travelling a distance s down the plane. Then which of the following will remain constant ?
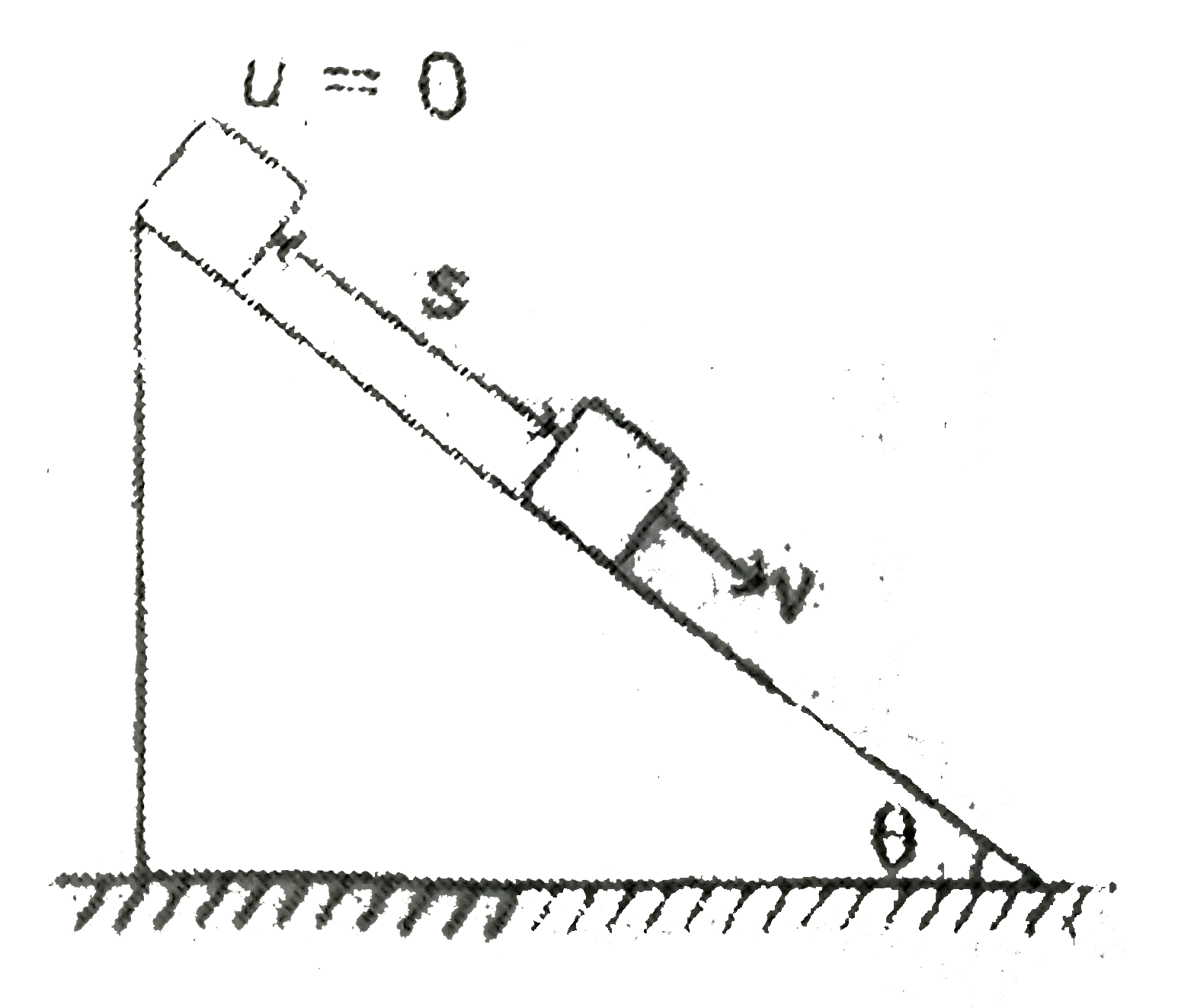
View SolutionSuppose y represents the work done and x the power, then dimensions of `(d^(2)y)/(dx^(2))` will be
View SolutionA spring and block are placed on a fixed smooth wedge as shown. Following conclusions can be drawn for the block.
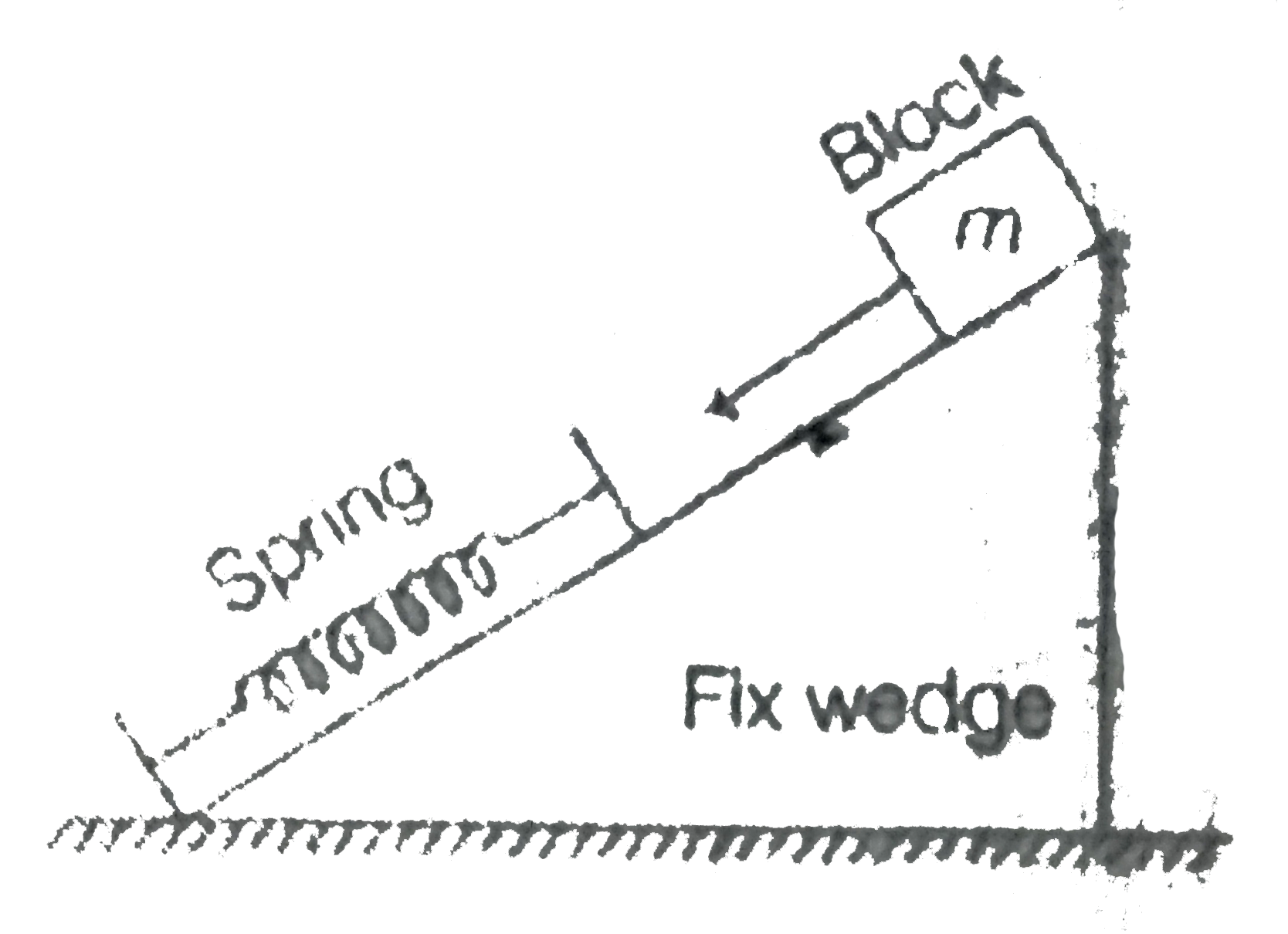
(i) magnitude of its momentum will be maximum when `F_("net")` on block is zero
(ii) its kinetic energy will be maximum when `F_("net")` on block is zero
(iii) kinetic energy of block is maximum when block just touches the spring
(iv) net force on block is maximum when KE = 0
View SolutionThe kinetic energy (KE) versus time graph for a particle moving along a straight line is as shown in the figure. The force versus time graph for the particle may be
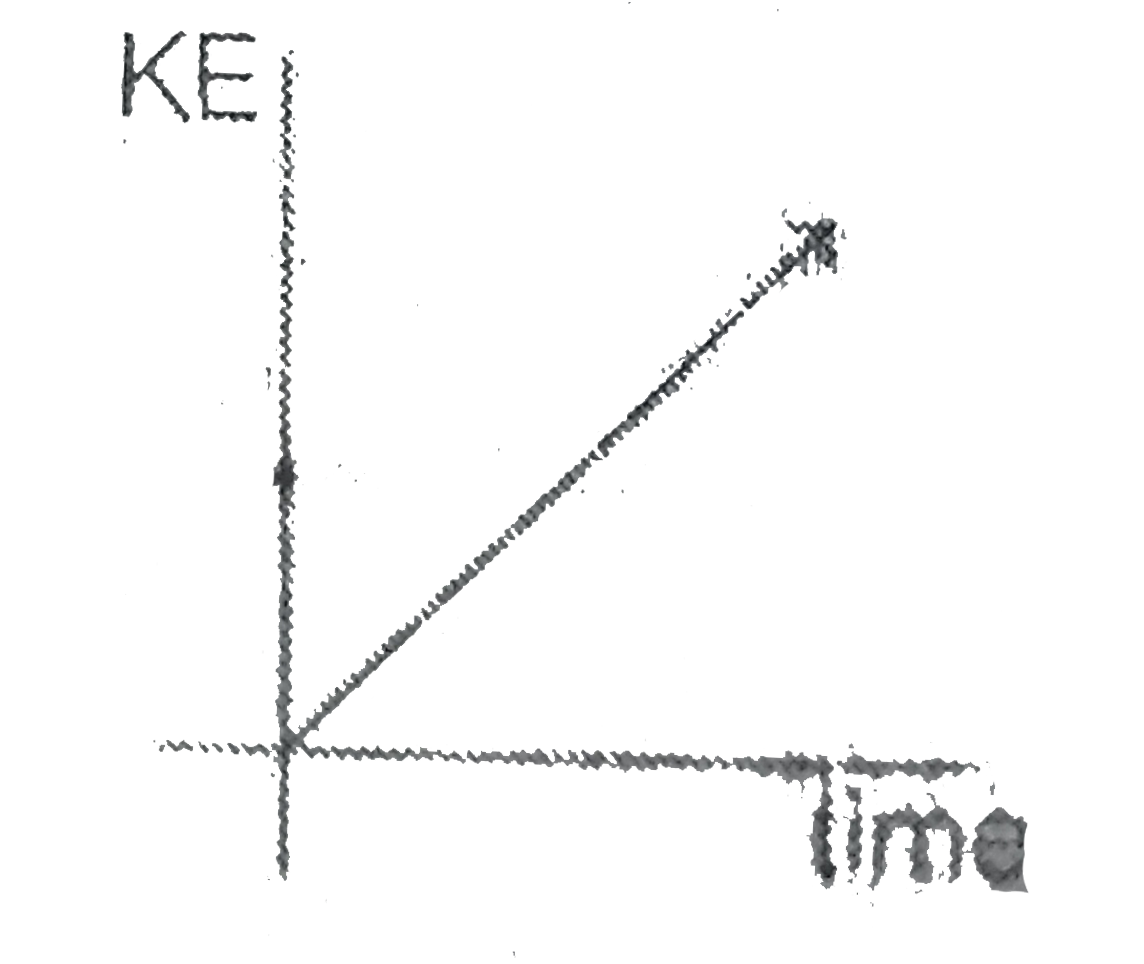
View Solution
Only One Option is Correct questions and complete solutions for chapter WORK, POWER AND ENERGY of DC PANDEY ENGLISH of Class 11