Complete Solutions to Examples of chapter CENTRE OF MASS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CENTRE OF MASS |
| DC PANDEY NEET | Examples |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
Two bodies of masses 1 kg and 2 kg are located at (1,2) and (-1,3), respectively. Calculate the coordinates of center of mass.
View SolutionTwo particles of masses 1kg and 2kg are located at `x=0` and `x=3m`. Find the position of their centre of mass.
View SolutionTwo points objects of mass 1.5g and 2.5g respectively are a distance of 16cm apart, the center of mass is at distance x from the object of mass 1.5g. Find the value of x
View SolutionThe position vectors of three particles of mass `m_(1) = 1kg, m_(2) = 2kg and m_(3) = 3kg` are `r_(1) = ((hat(i) + 4hat(j) +hat(k))`m, `r_(2) = ((hat(i)+(hat(j)+hat(k))`m and `r_(3) = (2hat(i) - (hat(j) -(hat(2k))`m, respectively. Find the position vector of their center of mass.
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles. Assume that D is situated at the origin.
View SolutionThree point masses `m_(1) = 2Kg, m_(2) = 4kg and m_(3)= 6kg` are kept at the three corners of an equilateral triangle of side 1 m. Find the locationo of their center of mass.
View SolutionThe linear density of a thin rod of length 1m lies as `lambda = (1+2x)`, where x is the distance from its one end. Find the distance of its center of mass from this end.
View SolutionA straight rod of length L has one of its end at the origin and the other at `X=L`. If the mass per unit length of the rod is given by `Ax` where A is constant, where is its centre of mass?
View SolutionFind the position of center of mass of the uniform lamina shown in figure, if small disc of radius `alpha/2` is cut from disc of radius a.
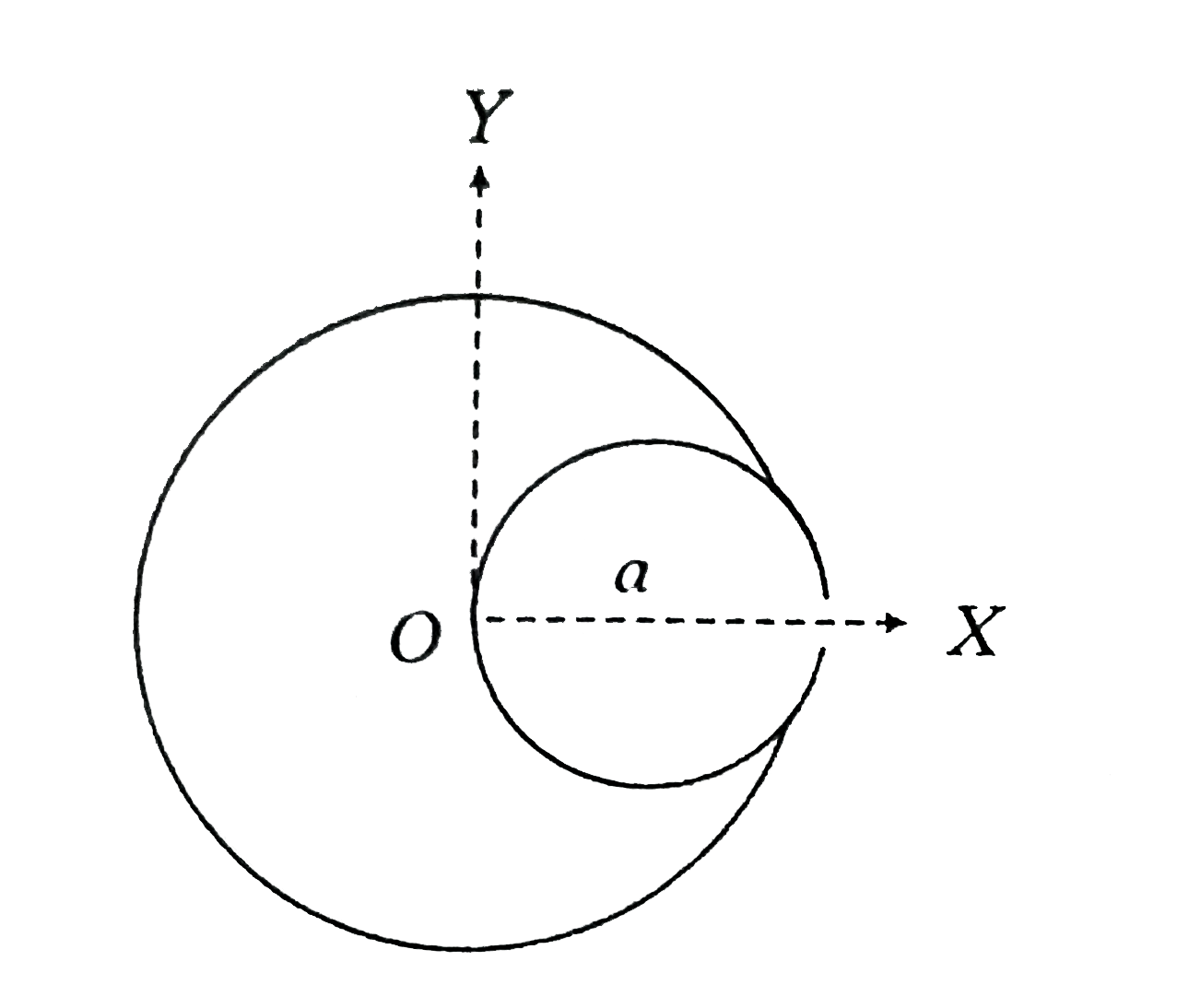
View SolutionA small disc of radius 2cm is cut from a disc of radius 6cm. If the distance their centers is 3.2cm, what is the shift in the center of mass of the disc?
View SolutionTwo identical rods each of mass `m` and length are connected as shown. Locate `c.m.`
View SolutionTwo blocks of masses `5 kg and 2 kg` are placed on a frictionless surface and connected by a spring. An external kick gives a velocity of `14 m//s` to the heavier block in the direction of lighter one. The magnitudes of velocities of two blocks in the centre of mass frame after the kick are respectively :
View SolutionFind the velocity of center of mass of the system shown in the figure.

View SolutionTwo particles of masses 2 kg and 4 kg are approaching each other with acceleration `1 ms^(-2)` and `2 ms^(-2)`, respectively, on a smooth horizontal surface. Find the acceleration of center of mass of the system.
View SolutionTwo particles of mass `m_(1)` and `m_(2)` are projected from the top of a tower. The particle `m_(1)` is projected vertically downward with speed u and `m_(2)` is projected horizontally with same speed. Find acceleration of CM of system of particles by neglecting the effect of air resistance.
View SolutionTwo particles of masses `2m` and `3m` are placed at separation `d` on a smooth surface. They move towards each other due to mutual attractive force. Find (a) acceleration of c.m. (b) Velocity of c.m. when separation between particles becomes `d//3`. ( c) At what distance from the initial position of mass `2m`, the particles collide.
View SolutionIn the arrangement shown in Figure, `m_A=2kg` and `m_B=1kg`. String is light and inextensible. Find the acceleration of centre of mass of both the blocks. Neglect friction everywhere.

View SolutionTwo particles A and B of mass 1 kg and 2 kg respectively are projected in the direction shown in figure with speeds `u_(A) = 200 ms^(-1)` and `u_(B) = 50 ms^(-1)`. Initially they were 90 m apart. Find the maximum height attained by the center of mass of the particles. Assume acceleration due to gravity to be constant. (Take, `g=10 ms^(-2)`.
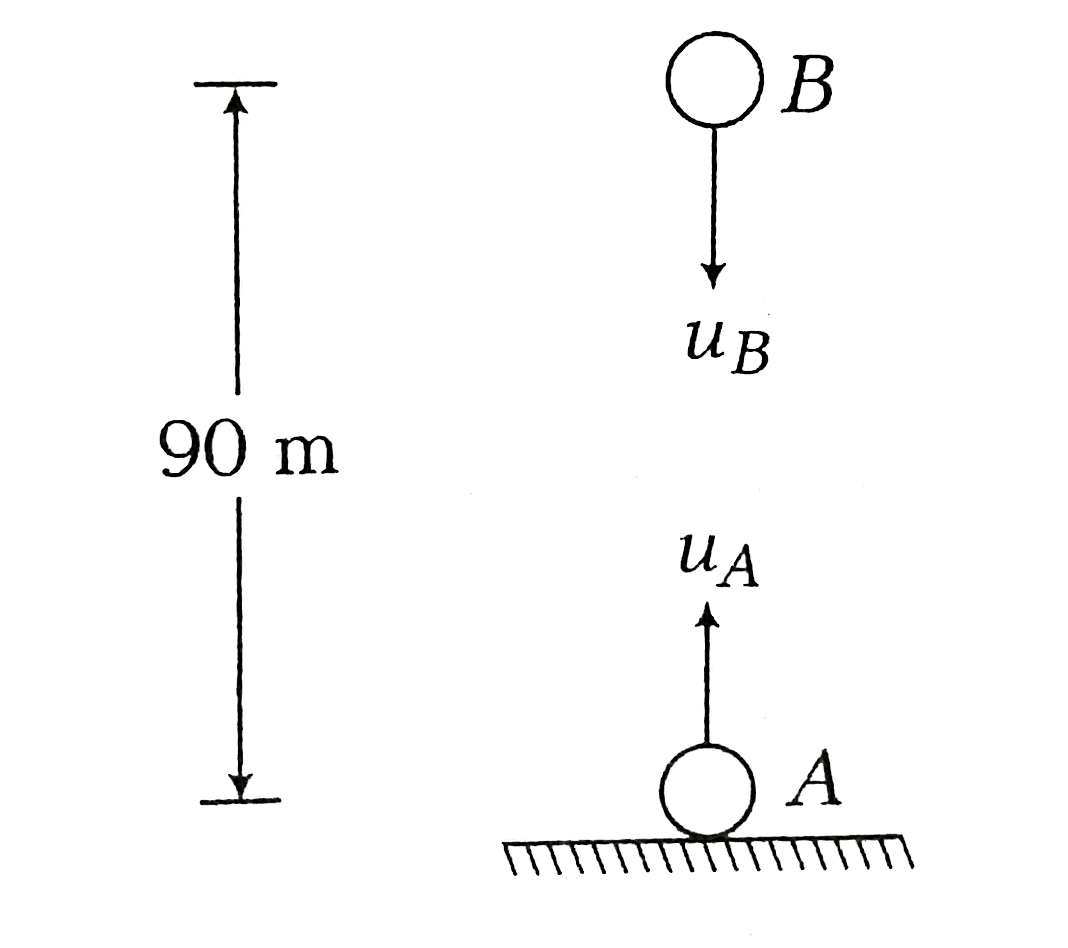
View SolutionA bullet mass 10gm is fired from a gun of mass 1 kg . If the recoil velocity is 5 `m//s`, the velocity of the muzzle is
View SolutionThe object at rest suddenly explodes into three parts with the mass ratio `2:1:1`. The parts of equal masses move at right angles to each other with equal speeds. What is the speed of the third part after the explosion?
View SolutionA 0.5 kg ball moving with a speed of 12 m/s strikes a hard wall at an angle of `30^(@)` with the wall. It is reflected with the same speed and at the same angle. If the ball is in contanct with the wall for 0.25 s, the average force aciton on the wall is

View SolutionA man of mass m is standing on a platform of mass M kept on smooth ice. If the man starts moving on the platform with a speed v relative to the platform with what velocity relative to the ice does the platform recoil?
View SolutionA wooden plank of mass `20kg` is resting on a smooth horizontal floor. A man of mass `60kg` starts moving from one end of the plank to the other end. The length of the plank is `10m`. Find the displacement of the plank over the floor when the man reaches the other end of the plank.

View SolutionA block of mass `M` with a semi - circular track of radius `R` rests on a smooth floor. A sphere of mass `m` and radius `r` is released from rest from `A`. Find the velocity of sphere and track , when the sphere reaches `B`.

View SolutionA particle of mass m is projectile with veoocity u making an angle of `45^(@)` with the horizontal.When the particle lands on the level ground, the magnitude of the change in its momentum will be
View SolutionA disc of mass 100 g is kept floating horizontally in air by firing bullets, each of mass 5 g with the same velocity at the same rate of 10 bullets per second. The bullets rebound with the same speed in opposite direction. Find the velocity of each bullet at the time of impact.
View SolutionTwo balls of masses m and 2m moving in opposite directions collide head on elastically with velocities `v` and `2v`. Find their velocities after collision.
View SolutionA simple pendulum of length 1 m has a wooden bob of mass 1 kg. It is struck by a bullet of mass `10^(-2)` kg moving with a speed of `2 xx 10^(2) m s^(-1)`. The height to which the bob rises before swinging back is (Take `g = 10 m s^(-2)`)
View SolutionA body falling on the ground from a height of 10m, rebounds to a height 2.5 m Calculate
(i) The percentage loss in KE
(ii) Ratio of the velocities of the body just before and just after the collision.
View SolutionA pendulum bob of mass `10^(-2) kg` is raised to a height `5 xx 10^(-2)` m and then released. At the bottom of its swing, it picks up a mass `10^(-3) kg`. To what height will the combined mass rise?

View SolutionA planck of mass `5kg` is placed on a frictionless horizontal plane. Further a block of mass `1kg` is placed over the plank. A massless spring of natural length `2m` is fixed to the plank by its one end. The other end of spring is compressed by the block by half of spring's natural length. They system is now released from the rest. What is the velocity of the plank when block leaves the plank? (The stiffness constant of spring is `100N//m`)

View SolutionAn object of mass `40kg` and having velocity `4 m//s` collides with another object of mass `60 kg` having velocity `2 m//s` . The loss of energy when the collision is perfectly inelastic is
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionThe mass of the railway carriage is 8000 kg which is moving with the speed of `54 km h^(-1)` collides with the another stationary carriage of same mass. Determine the loss in kinetic energy in this process.
View SolutionA ball is moving with velocity `2m//s` towards a heavy wall moving towards the ball with speed `1m//s` as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.

View SolutionA ball of mass 2kg moving with speed 5m/s collides directly with another ball of mass 3kg moving in the same direction with speed 4m/s. The coefficient of restitution is 2/3. Find the velocities of both ball after the collision.
View SolutionA block of mass 5 kg moves from left to right with a velocity of `2ms^(-1)` and collides with another block of mass 3 kg moving along the same line in the opposite direction with velocity `4 ms^(-1)`.
(i) If the collision is perfectly elastic, determine velocities of both the blocks after their collision.
(ii) If coefficient of restitution is 0.6, determine velocities of both the blocks after their collision.
View SolutionA particle of mass `2kg` moving with a velocity `5hatim//s` collides head-on with another particle of mass `3kg` moving with a velocity `-2hatim//s`. After the collision the first particle has speed of `1.6m//s` in negative x-direction, Find
(a) velocity of the centre of mass after the collision,
(b) velocity of the second particle after the collision.
(c) coefficient of restitution.
View SolutionAn object of mass m moving with speed u collides one dimentionally with another identical object at rest. Find their velocities after collision, if coefficient of restitution of collision is e.
View SolutionThree identical balls, ball I, ball II and ball III are placed on a smooth floor on a straight line at the separation of `10m` between balls as shown in figure. Initially balls are stationary. But I is given velocity of `10m//s` towards ball II, collision between balls I and II is inelastic with coefficient of restitution `0.5` but collision between balls II and III is perfectly elastic. What is the time interval between two consecutive collisions between ball I and II?

View Solution
Examples questions and complete solutions for chapter CENTRE OF MASS of DC PANDEY ENGLISH of Class 11