Three point masses are kept at the three corners of an equilateral triangle of side 1 m. Find the locationo of their center of mass.
To find the center of mass of three point masses located at the corners of an equilateral triangle, we can follow these steps:
Step 1: Identify the masses and their coordinates
We have three point masses:
- m1=2kg at point A (0, 0)
- m2=4kg at point B (1, 0)
- m3=6kg at point C
To find the coordinates of point C, we note that in an equilateral triangle with side length 1 m, the coordinates of point C can be determined using trigonometry:
- The x-coordinate of C is 12 (half the base).
- The y-coordinate of C is √32 (height of the triangle).
Thus, the coordinates of point C are (12,√32).
Step 2: Write down the formula for the center of mass
The center of mass R for a system of point masses is given by:
R=m1r1+m2r2+m3r3m1+m2+m3
where ri are the position vectors of the masses.
Step 3: Substitute the values into the formula
Substituting the values into the formula:
- m1=2kg,r1=(0,0)
- m2=4kg,r2=(1,0)
- m3=6kg,r3=(12,√32)
The total mass M is:
M=m1+m2+m3=2+4+6=12kg
Step 4: Calculate the x-coordinate of the center of mass
Calculating the x-coordinate:
xcm=m1x1+m2x2+m3x3M=2⋅0+4⋅1+6⋅1212
=0+4+312=712
Step 5: Calculate the y-coordinate of the center of mass
Calculating the y-coordinate:
ycm=m1y1+m2y2+m3y3M=2⋅0+4⋅0+6⋅√3212
=0+0+3√312=3√312=√34
Step 6: Combine the coordinates to find the center of mass
Thus, the coordinates of the center of mass R are:
R=(712,√34)
Final Answer
The location of the center of mass is:
(712,√34)
We have three point masses:
- m1=2kg at point A (0, 0)
- m2=4kg at point B (1, 0)
- m3=6kg at point C
- The x-coordinate of C is 12 (half the base).
- The y-coordinate of C is √32 (height of the triangle).
The center of mass R for a system of point masses is given by:
R=m1r1+m2r2+m3r3m1+m2+m3
where ri are the position vectors of the masses.
Substituting the values into the formula:
- m1=2kg,r1=(0,0)
- m2=4kg,r2=(1,0)
- m3=6kg,r3=(12,√32)
M=m1+m2+m3=2+4+6=12kg
Calculating the x-coordinate:
xcm=m1x1+m2x2+m3x3M=2⋅0+4⋅1+6⋅1212
=0+4+312=712
Calculating the y-coordinate:
ycm=m1y1+m2y2+m3y3M=2⋅0+4⋅0+6⋅√3212
=0+0+3√312=3√312=√34
Thus, the coordinates of the center of mass R are:
R=(712,√34)
The location of the center of mass is:
(712,√34)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Check points
50 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Taking it together
73 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
Three point masses m1,m2 and m3 are located at the vertices of an equilateral triangle of side α. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m1?
View SolutionThree point masses m1,m2 and m3 are located at the vertices of an equilateral triangle of side α. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m1?
View Solution
Knowledge Check
Three particles of masses 1kg,32kg,and2kg are located the vertices of an equilateral triangle of side a. The x,y coordinates of the centre of mass are.
Aa. 5a9,2a3√3Bb. 2a3√3,5a9Cc. 5a9,2a√3Dd. 2a√3,5a9
Three masses 2 kg , 3kg and 4kg are lying at the corners of an equilateral triangle of side I. The X coordinate of center of mass is
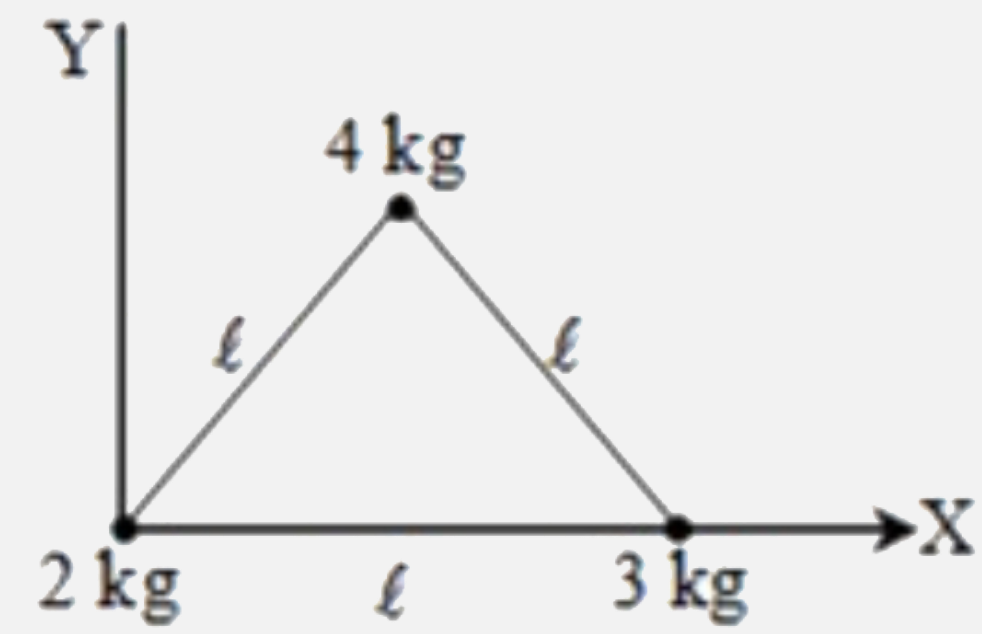
View SolutionThree particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
View SolutionThree masses of 1kg, 2kg, and 3kg, are placed at the vertices of an equilateral triangle of side 1m. Find the gravitational potential energy of this system.
Take G=6.67×10−11N−m2/kg2.
View SolutionThree balls of masses 1kg,2kgand3kg are arranged at the corners of an equilateral triangle of side 1m. What will be the moment of inertia of the system and perpendicular to the plane of the triangle.
View SolutionThree masses of 1kg, 2kg, and 3kg, are placed at the vertices of an equilateral triangle of side 1m. Find the gravitational potential energy of this system.
Take G=6.67×10−11N−m2/kg2.
View SolutionThree masses 3, 4 and 5 kg are placed at the centre of an equiliteral triangle of 1 m sides. Locate its centre of mass.
View SolutionThree particles of masses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre of mass of the system.
View Solution
