Complete Solutions to Check points of chapter CENTRE OF MASS of Class 11 book with complete answers and questions

The position of centre of mass of system of particles at any moment does not depend on.

The center of mass of a system of two particles divides the distance between them.

Two bodies of masses `1` kg and `2` kg are lying in `xy` plane at `(-1,2)` and `(2,4)` respectively. What are the coordinates of the centre of mass ?

In a carbon monoxide molecule, the carbon and the oxygen atoms are separated by a distance `1.2xx10^-10m`. The distance of the centre of mass from the carbon atom is

Figure shows a composite system of two uniform rods of lengths as indicated. Then the coordinate of the center of mass of the system of rods are

All the particles of a body situated at distance `R` from the origin. The distance of the center of mass of the body from the origin is

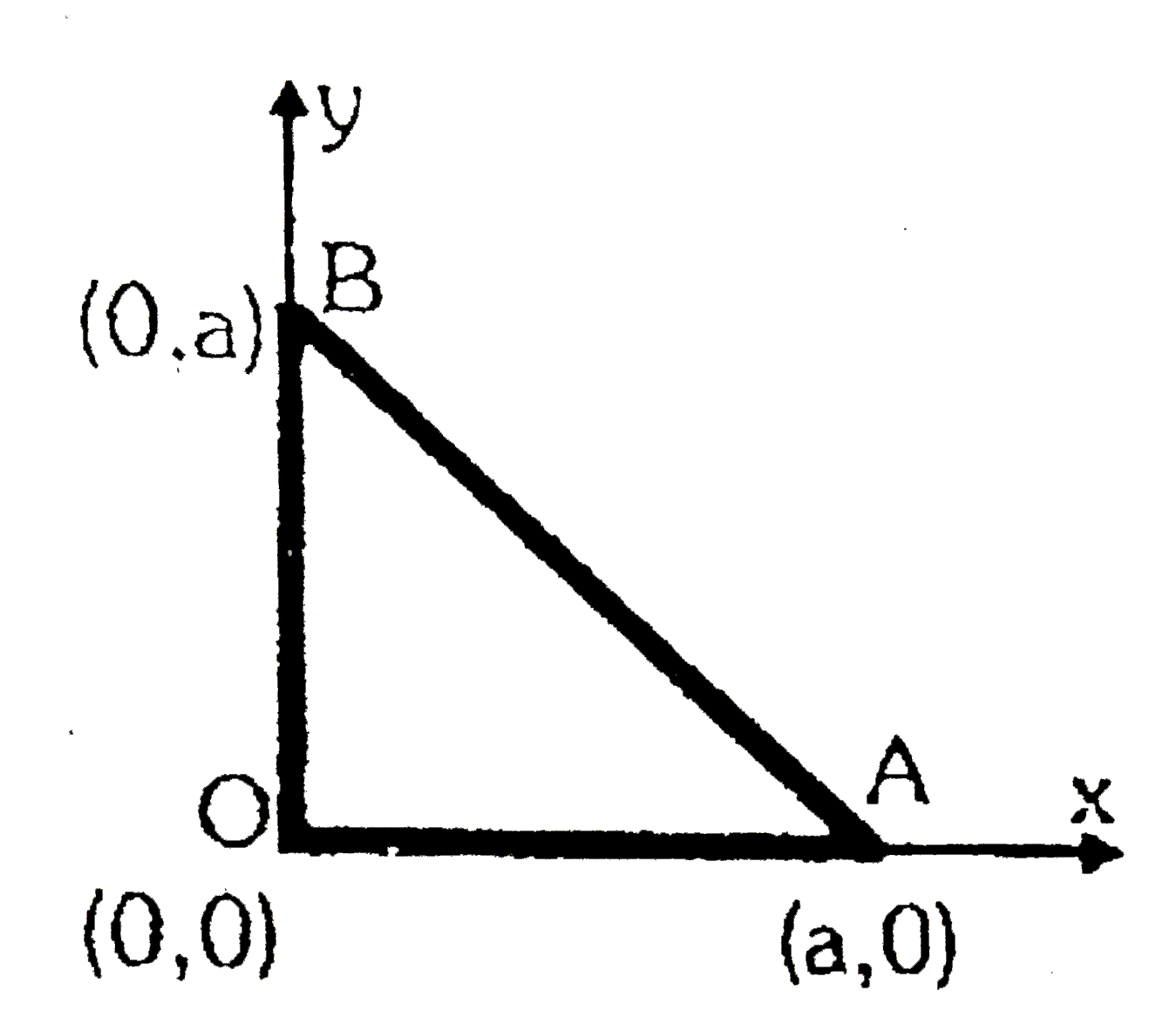
A uniform metre rod is bent into `L` shape with the bent arms at `90^@` to each other. The distance of the centre of mass from the bent point is

Three point masses `m_(1), m_(2) and m_(3)` are placed at the corners of a thin massless rectangular sheet `1.2m xx 1m)` as shown. Center of mass will be located at the point.

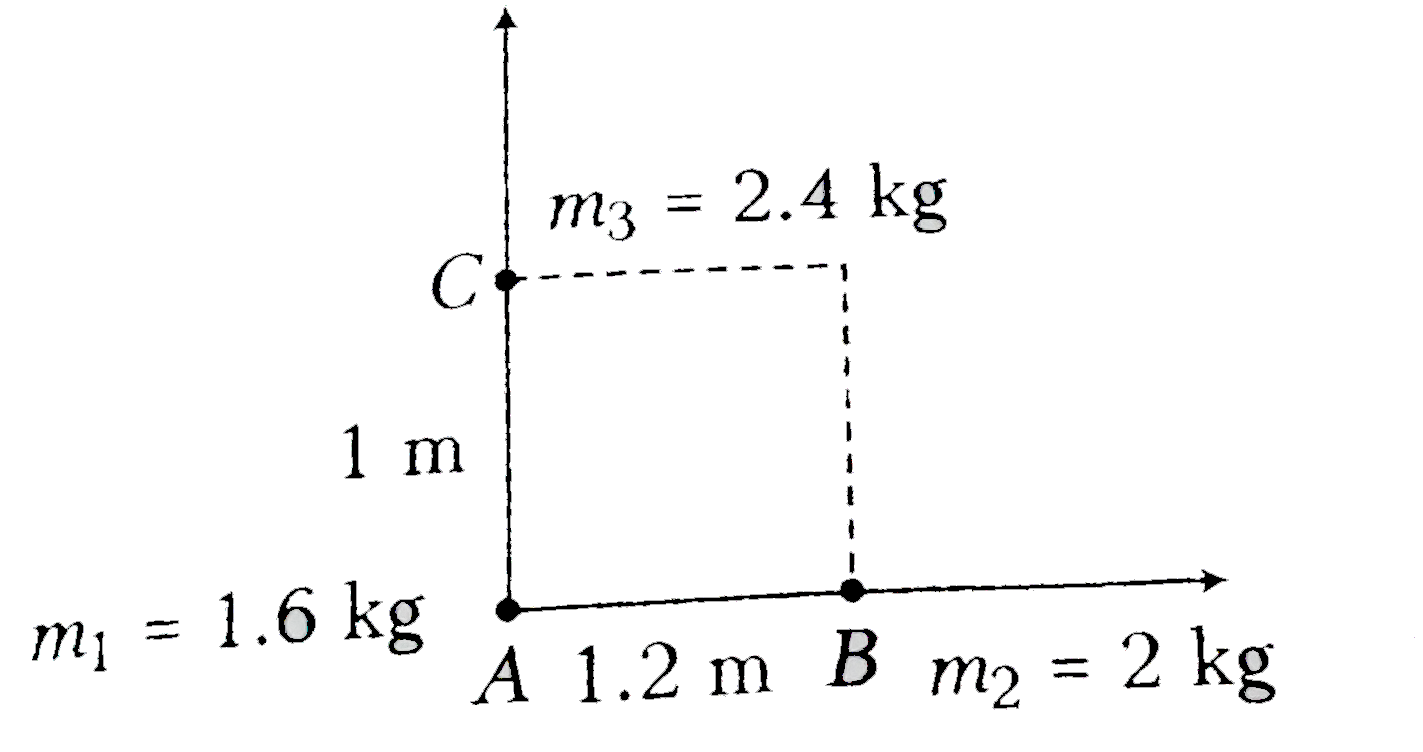
Three rods of the same mass are placed as shown in the figure. Calculate the coordinates of the centre of mass of the system.

Centre of mass of three particles of masses 1 kg, 2 kg and 3 kg lies at the point (1, 2, 3) and centre of mass of another system of particles 3 kg and 2 kg lies at the point (-1, -3, -2). Where should we put a particle of mass 5 kg so that the centre of mass of entire system lies at the centre of mass of first system?

Four particles of masses `m_(1) = 2m , m_(2) = 4 m , m_(3) = m ` and `m_(4)` are placed at four corners of a square . What should be the value of `m_(4)` , so that the centre of mass of all the four particles are exactly at the centre of the square ?

Four rods AB, BC, CD and DA have mass m,2m,3m and 4m respectively. The center of mass of all the four rods

Three identicle particle each of mass `1 kg` are placed with their centres on a straight line. Their centres are marked `P, Q and R` respectively. The distance of centre of mass of the system from `P` is.

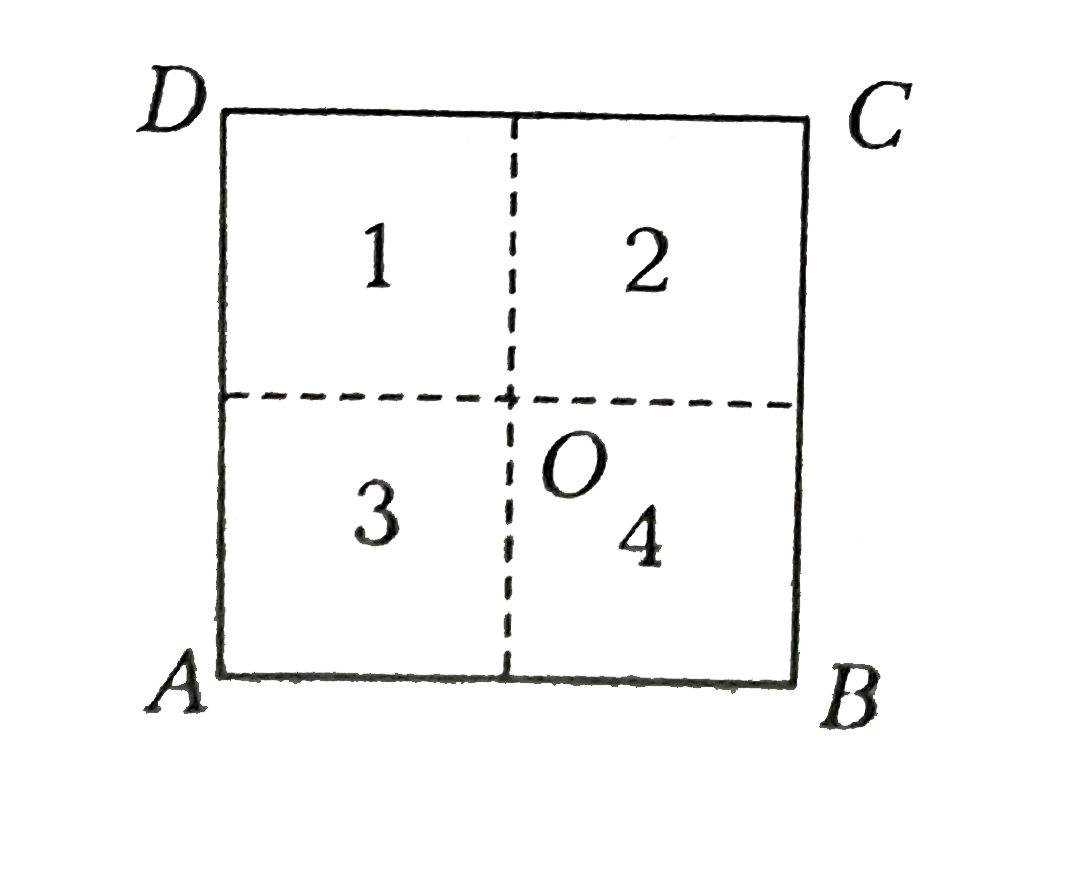
A square plate of side 20cm has uniform thickness and density. A circular part of diameter 8cm is cut out symmetrically and shown in figure. The position of center of mass of the remaining potion is

A uniform metal disck of radius R is taken and out of it a disc of diameter R is cut-off from the end. The center of mass of the remaining part will be

A body at rest breaks into two pieces of equal masses. The parts will move

A body falling vertically downwards under gravity breaks in two parts of unequal masses. The centre of mass of the two parts taken together shifts horizontally towards

Two balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls while in air

Consider a system of two identical particles. One of the particles is at rest and the other has an acceleration. The centre of mass has an acceleration.

Two particles A and B intiallly at rest, move towards each other under a mutual force of attraction. AT the instant when the speed of A is v and the speed of B is 2 v, the speed of the centre of mass of the system is

Two balls of equal mass are projected from a tower simultaneously with equal speeds. One at angle `theta` above the horizontal and the other at the same angle `theta` below the horizontal. The path of the center of mass of the two balls is

One projectile moving with velocity v in space, gets burst into 2 parts of masses in the ratio `1:3`. The smaller part becomes stationary. What is the velocity of thhe other part?

A bomb of mass `9kg` explodes into two pieces of masses `3kg` and `6kg`. The velocity of mass `3kg` is `16ms^-1`. The kinetic energy of mass `6kg` is

Two blocks of masses `10 kg` and `4 kg` are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of `14 m//s` to the heavier block in the direction of the lighter block. The velocity of the centre of mass is

A ball kept in a close box moves in the box making collisions with the walls. The box is kept on a smooth surface. The velocity of the centre of mass

A meter stick is placed vertically at the origin on a frictionles surface. A gentle push in +x direction is given to the top most point of the rod. When it has fallen completely x-coordinate of center of rod is at

Two bodies having masses `m_(1)` and `m_(2)` and velocities `v_(1)` and `v_(2)` colide and form a composite system. If `m_(1)v_(1) + m_(2)v_(2) = 0(m_(1) ne m_(2)`. The velocity of composite system will be

Two particles of equal mass have coordinates (2m,4m,6m) and (6m,2m,8m). Of these one particle has a velocity `v_(1) = (2i)ms^(-1)` and another particle has a velocity `v_(2) = (2j)ms^(-1)` at time t=0. The coordinate of their center of mass at time t=1s will be

An isolated particle of mass `m` is moving in horizontal plane` xy` along the `x`-axis, at a certain height above the ground. It suddenly explodes into two fragment of masses `m//4` and `3m//4`. An instant later, the smaller fragment is at `y=+15` cm. The larger fragment at this instant is at

Blockes A and B are resting on a smooth horizontal surface given equal speeds of `2ms^(-1)` in opposite sense as shown in the figure.

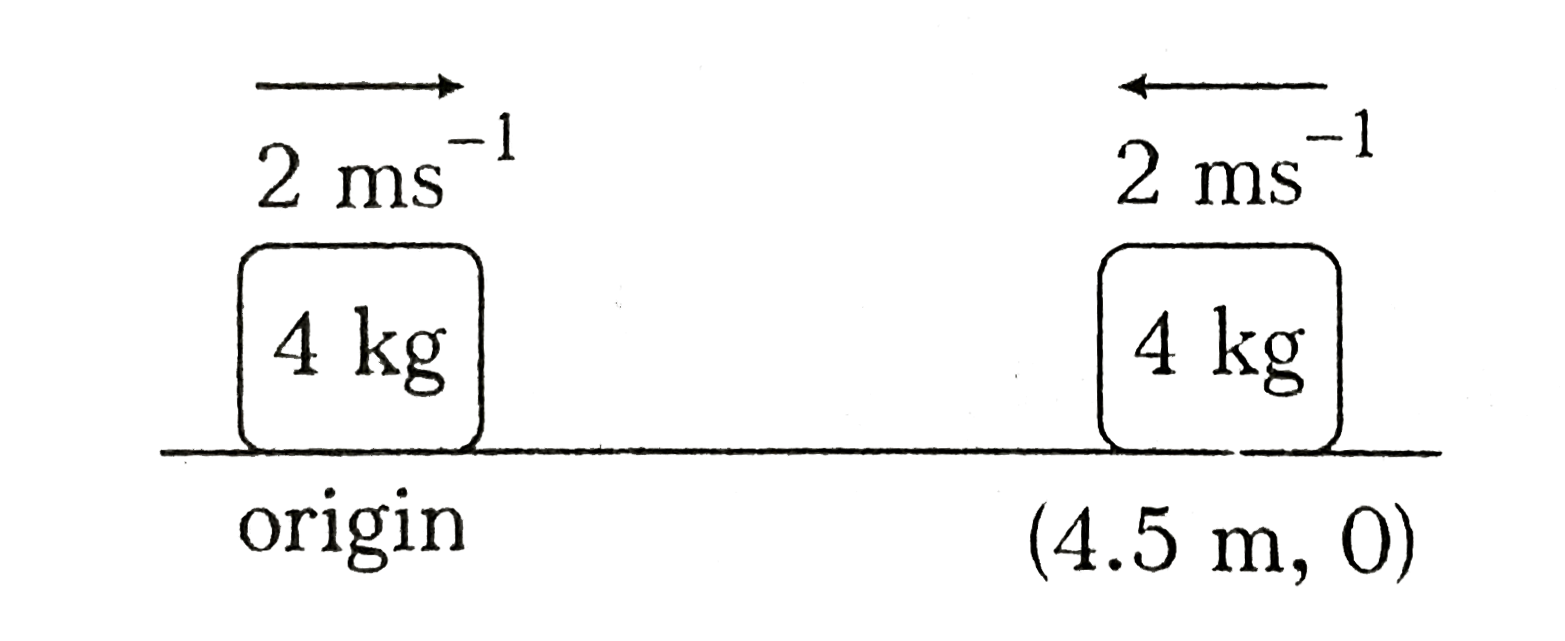
At t=0, the position of blocks are shown, then the coordinates of center of mass t=3s will be

A man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is

An object of mass 3m splits into three equal fragments. Two fragments have velocities `vhatj` and `v hati`. The velocity of the third fragment is

A stationary bomb explode into two parts of masses 3kg and 1kg. The total KE of the two parts after explosioons is 2400J. The KE of the smaller part is

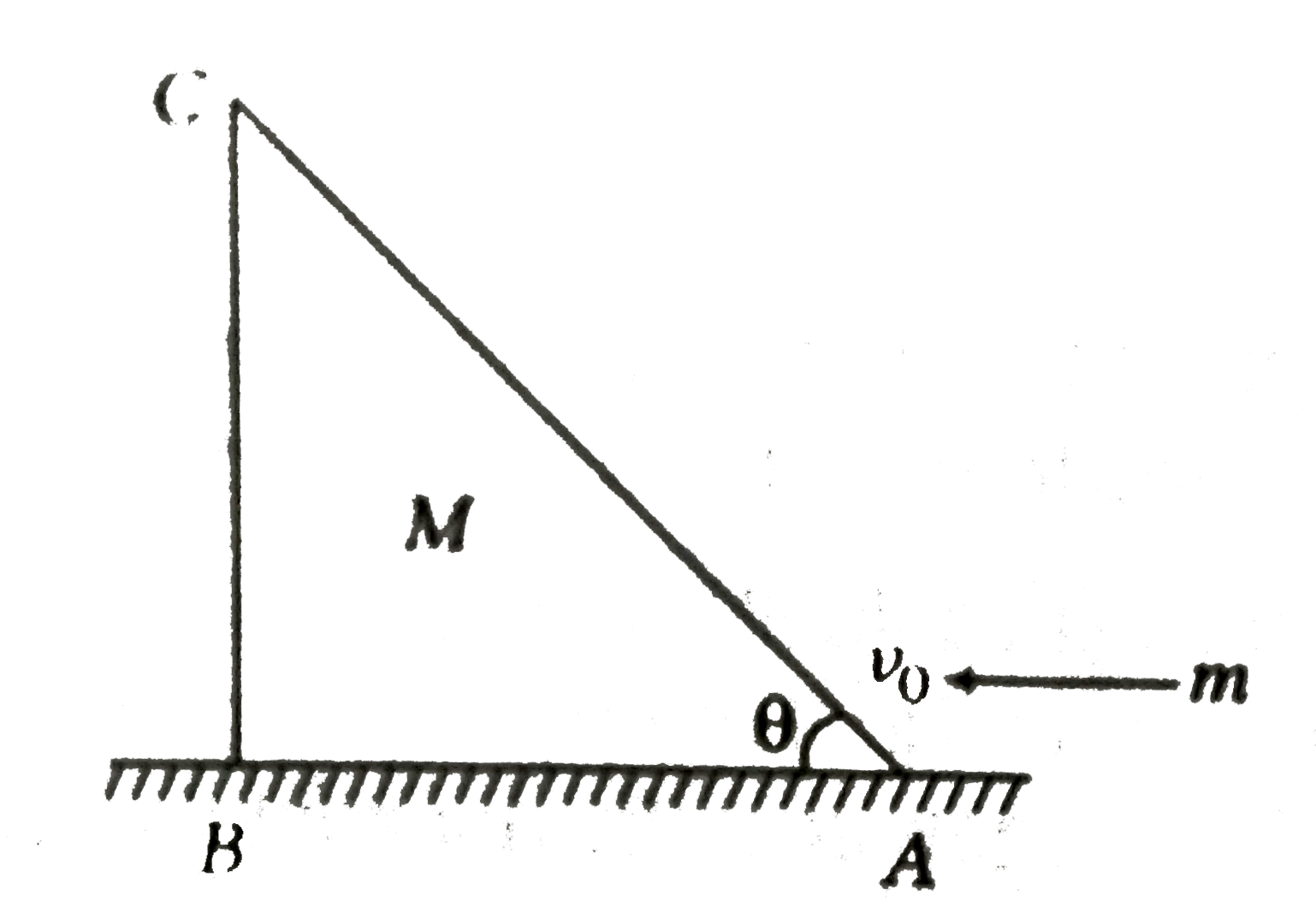
A shell of mass m is moving horizontally with velocity `v_(0)` and collides with the wedge of mass M just above points A, as shown in the figure. As a consequences, wedge starts to move towards left and the shell returns with a velocity in xy-plance. The principle of conservation of momentum can be applied for

A shell is fired from a cannon with a velocity V at an angle `theta` with the horizontal direction. A the highest point i its path, it explodes into two pieces of equal masses. One of the pieces retraces its path to the cannon. The speed of the other priece immediately after the explocison is

In an elastic collision

If a body of mass m collides head on, elastically with velocity u with another identical boday at rest. After collision velocty of the second body will be

A ball hits a floor and rebounds after an inelastic collision. In this case

A body of mass `M_(1)` collides elastically with another mass `M_(2)` at rest. There is maximum transfer of energy when :

Two particles of mass `m_(A)` and `m_(B)` and their velocities are `V_(A)` and `V_(B)` respectively collides. After collision they interchanges their velocities, then ratio of `m_(A)/m_(B)` is

Two perfectly elastic particles `A` and `B` of equal masses travelling along a line joining them with velocities `15 m//s` and `10m//s` respectively collide. Their velocities after the elastic collision will be (in m/s) respectively

The collision of two balls of equal mass takes place at the origin of coordinates. Before collision, the components of velocities are (`v_(x) = 50cm^(-1)` , `v_(y) = 0`) and `(v_(x) = -40cm^(-1)` and `v_(y) = 30cms^(-1)`. The first ball comes to rest after collision. The velocity (components `v_(x)` and `v_(y)` respectively) of the second ball are

A mass of `0.5 kg` moving with a speed of `1.5 m//s` on a horizontal smooth surface, collides with a nearly weightless spring of force constant `k =50 N//m` The maximum compression of the spring would be.

Two perfectly elastic particles A and B of equal mass travellinng along the line joining them with velocities `15ms^(-)` and `10ms^(-)`. After collision, their velocities will be

A smooth sphere of mass M moving with velocity u directly collides elastically with another sphere of mass m at rest. After collision their final velocities are V and v respectively. The value of v is

A body of mass `m_(1)` moving with a velocity `3 m//s` collides with another body at rest of `m_(2)` . After collision the velocities of the two bodies are `2 m//s` and `5 m//s` , respectively , along the direction of motion of `m_(1)`. The ratio `m_(1)//m_(2)` is

A body of mass `m` moving with velocity `v` collides head on with another body of mass `2 m` which is initially at rest. The ratio of K.E. of colliding body before and after collision will be

The two diagrams show the situations before and after a collision between two spheres A and B of equal radii moving along the same straight line on a smooth horizontal surface. The coefficient of restitution e is

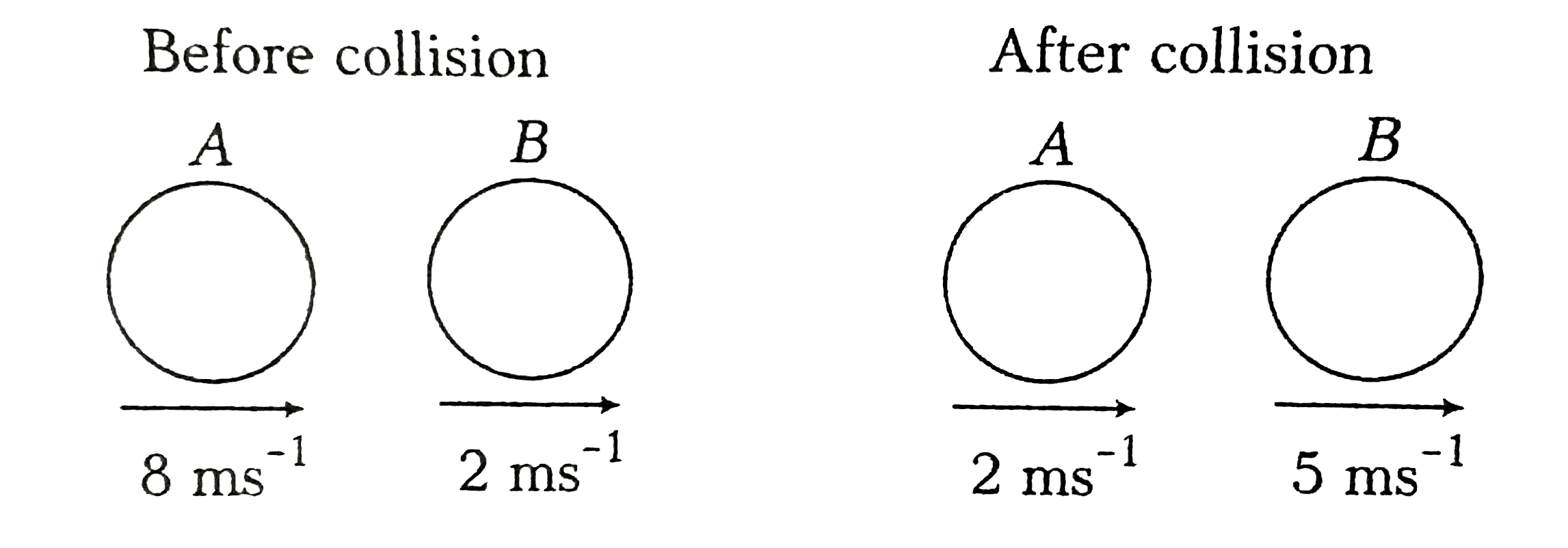
A block of mass m moving at speed `upsilon` collides with another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.

Sphere A of mass `m` moving with a constant velocity `u` hits another stationary sphere B of the same mass. If `e` is the co-efficient of restitution, then ratio of velocities of the two spheres `v_(A):v_(B)` after collision will be :