Complete Solutions to (C) Chapter Exercises of chapter ROTATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATION |
| DC PANDEY NEET | (C) Chapter Exercises |
| Number Of Questions | 39 |
| Academic Year | 2023-24 |
A wheel of radius 10 cm can rotate freely about its centre as shown in figure. A string is wrapped over its rim and is pulled by a force of 5.0 N. It is found that the torque produces an angular acceleration 2.0 `rad s^-2` in the wheel. Calculate the moment of inertia of the wheel.

View SolutionTwo uniform spheres A (Hollow) and B (solid) of same radius R (
View SolutionA disc and a solid sphere of same radius but different masses roll off on two inclined planes of the same altitude and length. Which one of the two objects gets to the bottom of the plane first ?
View SolutionA uniform circular disc of radius `50 cm` at rest is free to turn about an axis, which is perpendicular to the plane and passes through its centre. It is subjected to a torque which produces a constant angular acceleration of `2.0 rad//s^(2)`. Its net acceleration in `m//s^(2)` at the end of `2.0 s` is approximately
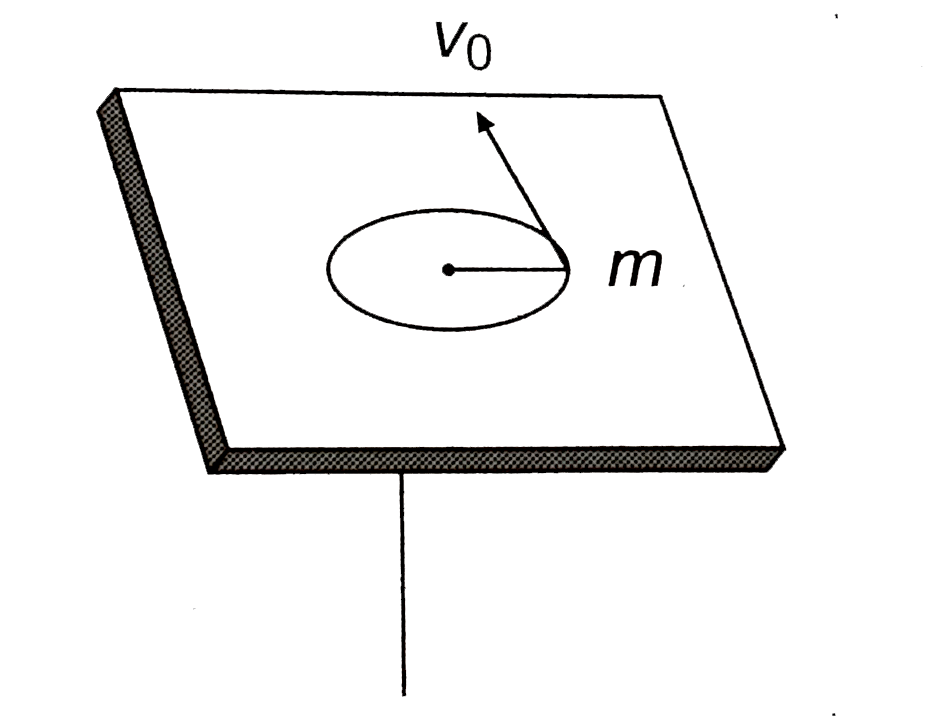
View SolutionA mass `m` moves in a circles on a smooth horizontal plane with velocity `v_(0)` at a radius `R_(0)`. The mass is attached to string which passes through a smooth hole in the plane as shown.
The tension in string is increased gradually and finally `m` moves in a circle of radius `(R_(0))/(2)`. the final value of the kinetic energy is
View SolutionThree idential spherical shells each of mass `m` and radius `r` are placed as shown in Fig. Consider an axis XX' which is touching the two shells and passing through diameter of third shell. Moment of Inertia of the system consisting of these three spherical shells about XX' as axis is :
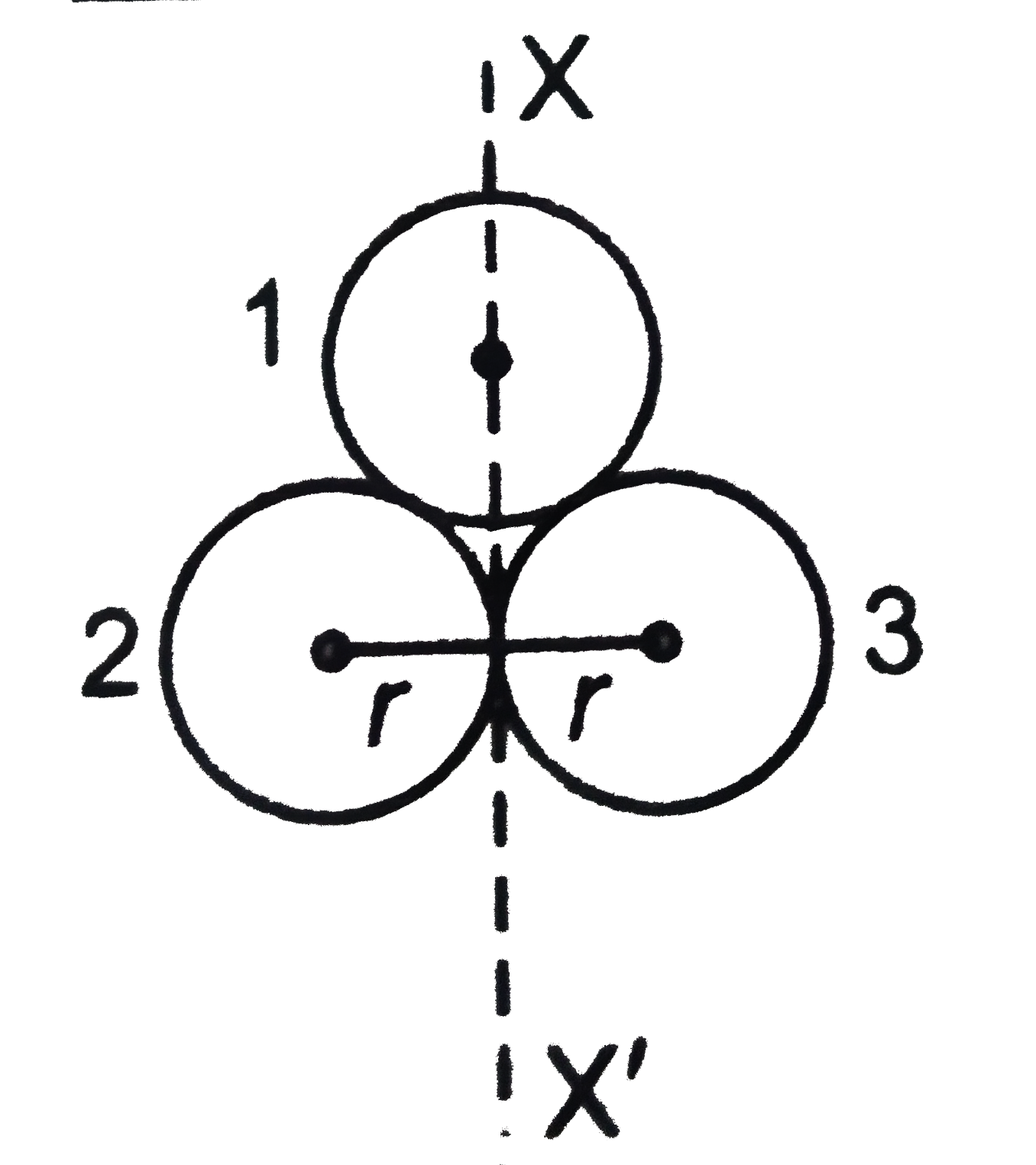
View Solution
View Solution
View SolutionA particle travels in a circle of radius 20 cm at a uniformly increasing speed. If the speed changes from `8 ms^(-1)` to `9 ms^(-1)` in 2s, what would be the angular acceleration in `"rad s"^(-2)` ?
View SolutionA solid sphere of radius `r` is rolling on a horizontal surface. The ratio between the rotational kinetic energy and total energy.
View SolutionIf two circular discs A and B are of same mass but of radii r and 2r respectively, then the moment of inertia of A is
View SolutionChoose the wrong statement.
View SolutionTwo particle A and B are moving as shown in the figure
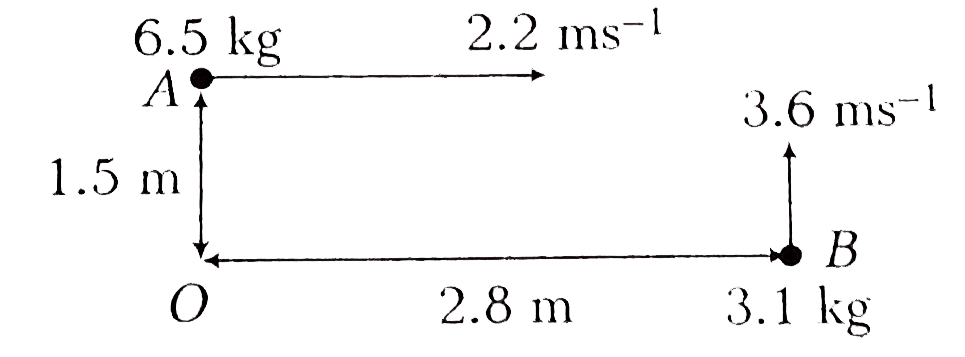
Their total angular momentum about the point O is
View SolutionA rod of mass 5 kg is connected to the string at point B. The span of rod is along horizontal. The other end of the rod is hinged at point A. If the string is massless, then the reaction of hinge at the instant when string is cut, is (Take, `g=10 ms^(-2)`)
View Solution
View SolutionA ring of radius 0.5 m and mass 10 kg is rotating about its diameter with angular velocity of `20 rad s^(-1)`. Its kinetic energy is
View SolutionA uniform sphere of mass `500 g` rolls without slipping on a plane surface so that its centre moves at a speed of `0.02 m//s`.
The total kinetic energy of rolling sphere would be (in `J`)
View SolutionA rotating wheel changes angular speed from 1800 rpm to 3000 rpm in 20 s. What is the angular acceleration assuming to be uniform?
View SolutionThe moment of inertia of ring about an axis passing through its diameter is `I`. Then moment of inertia of that ring about an axis passing through its centre and perpendicular to its plane is
View SolutionTwo bodies have their moments of inertia `I` and `2I`, respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular velocity will be in the ratio
View SolutionA body having a moment of inertia about its axis of rotation equal to `3 "kg-m"^(2)` is rotating with angular velocity of `3 "rad s^(-1)`. Kinetic energy of this rotating body is same as that of a body of mass `27 kg` moving with a velocity `v`. The value of `v` is
View SolutionA uniform solid spherical ball is rolling down a smooth inclined plane from a height h. The velocity attained by the ball when it reaches the bottom of the inclined plane is v. If ball when it reaches the bottom of the inclined plane is v. If the ball is now thrown vertically upwards with the same velocity `v`, the maximum height to which the ball will rise is
View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the intial angular acceleration of the rod is

View SolutionA small object of uniform density rolls up a curved surface with an initial velocity v'. It reaches upto to maximum height of `(3v^(2))/(4g)` with respect to the initial position. The object is
View SolutionThe conservation of angular momentum demands that
View SolutionThe moment of inertia `(I)` and the angular momentum `(L)` are related by the expression
View SolutionThe moment of ineria `(I)` of a sphere of radius R and mass M is given by
View SolutionA particle mass `m` is attched to a thin uniform rod of length a at a distance of `(a)/(4)` from the mid-point C as shown in the figure. The mass of the rod is `4m`
The moment of inertia of the combined system about an axis passing through O and perpendicular to the rod is
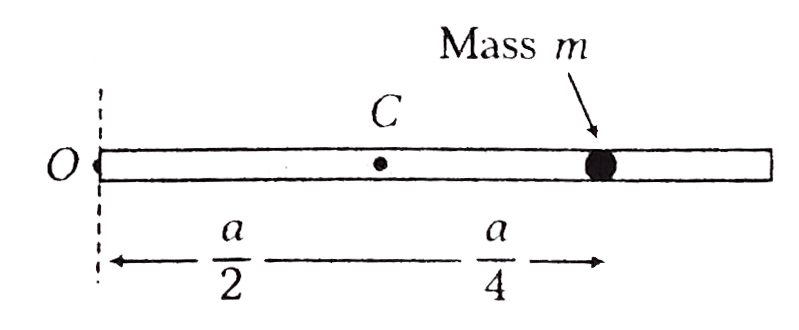
View SolutionA particle moving in a circular path has an angular momentum of L. If the frequency of rotation is halved, then its angular momentum becomes
View SolutionThe torque of a force `F = 2 hat(i) - 3 hat(j) +5 hat(k)` acting at a point whose position vector `r = 3 hat(i) - 3 hat(j) +5 hat(k)` about the origin is
View SolutionMoment of inertia of a ring of radius R about a diametric axis is `25 "kg m"^(2)`. The `MI` of the ring about a parallel axis at a distance `R` from the centre is
View SolutionA wheel having moment of inertia `2 "kg-m"^(2)` about its vertical axis, rotates at the rate of 60 rpm about this axis. The torque which can stop the wheel's rotation in one minute would be
View SolutionWhat is the moment of inertia of solid sphere of density `rho` and radius `R` about its diameter ?
View SolutionThe radius of gyration of a body depends upon
View SolutionTwo discs have same mass and thickness. Their materials are of densities `rho_(1)` and `rho_(2)`. The ratio of their moment of inertia about central axis will be
View SolutionIf a disc starting from rest acquires an angular velocity of `240 "rev min"^(-1)` in 10 s, then its angular acceleration will be
View SolutionA thin hollow sphere of mass m is completely filled with a liquid of mass m. When the sphere rolls with a velocity v kinetic energy of the system is (neglect friction)
View SolutionThe moment of inertia of a circular loop of radius R, at a distance of `R//2` around a rotating axis parallel to horizontal diameter of loop is
View SolutionA rod of length L is composed of a uniform length 1/2 L of wood mass is `m_(w)` and a uniform length 1/2 L of brass whose mass is `m_(b)`. The moment of inertia `I` of the rod about an axis perpendicular to the rod and through its centre is equal to
View Solution
(C) Chapter Exercises questions and complete solutions for chapter ROTATION of DC PANDEY ENGLISH of Class 11