Complete Solutions to (A) Chapter Exercises of chapter ROTATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATION |
| DC PANDEY NEET | (A) Chapter Exercises |
| Number Of Questions | 83 |
| Academic Year | 2023-24 |
The angular momentum of a system of particles is conserved
View SolutionIf a person standing on a rotating disc stretches out his hands, the angular speed will
View SolutionWhen a disc rotates with uniform angular velocity, which of the following is not true ?
View SolutionA ring of diameter 0.4 m and of mass 10 kg is rotating about its axis at the rate of 1200 rpm. The angular momentum of the ring is
View SolutionA uniform disc of radius a and mass m, is rotating freely with angular speed `omega` in a horizontal plane about a smooth fixed vertical axis through its centre. A particle, also of mass m, is suddenly attached to the rim of the disc of the disc and rotates with it. The new angular speed is
View SolutionA uniform square plate has a small piece `Q` of an irregular shape removed and guled to the centre of the plate leaving a hole behind in figure. The moment of inertia about the z-axis is then,
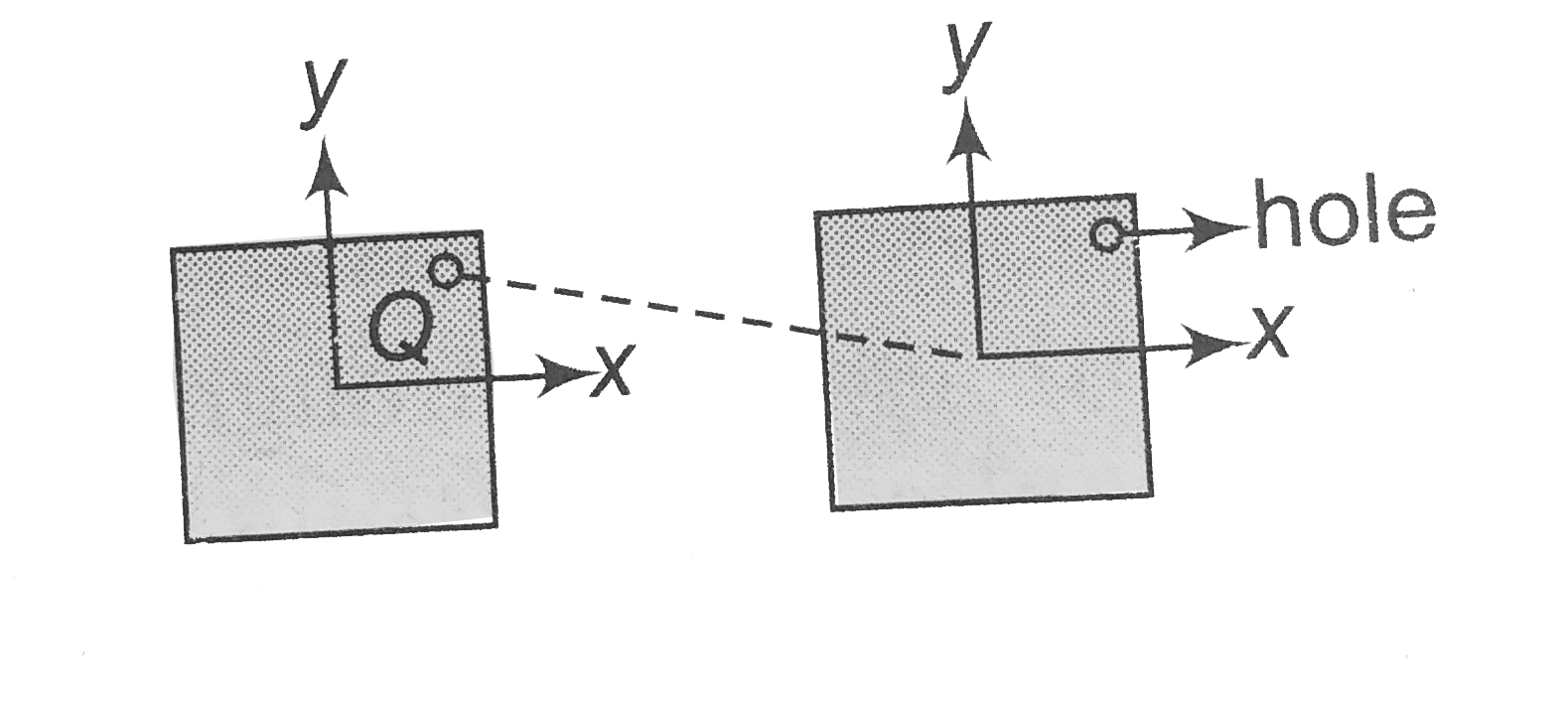 .
.
View SolutionA diver is able to cut through water in a swimming pool. Which property of matter does this observation show?
View SolutionA body is in pure rotation. The linear speed 'v' of a particle, the distance 'r' of the particle from the axis and the angular velocity `omega` of the body are related as `omega=v/r`. Thus
View SolutionThe rotational kinetic energy of a body is E and its moment of inertia is `I`. The angular momentum is
View SolutionA body is under the action of two equal and oppositely directed forces and the body is rotating with constant non-zero angular acceleration. Which of the following cannot be the separation between the lines of action of the forces ?
View SolutionA particle performing uniform circular motion has angular momentum `L`. If its angular frequency is double and its kinetic energy halved, then the new angular momentum is :
View SolutionMoment of a force of magnitude 10 N acting along positive y-direction at point `(2m,0,0)` about the point `(0,1m,0)` in N-m is
View SolutionThe radius of gyration of a uniform rod of length `L` about an axis passing through its centre of mass is
View SolutionFive particles of mass 2 kg are attached to the rim of a circular disc of radius 0.1 m & negligible mass. Moment of inertia of the system about an axis passing through the centre of the disc & perpendicular to its plane is
View SolutionA particle is moving in a circular orbit with constant speed. Select wrong alternate.
View SolutionIf the equation for the displacement of a particle moving on a circle path is given by, `theta = 2t^(2)+0.5` where, `theta` is in radian and `t` is in second, then the angular velocity of the particle after 2 s is
View SolutionA wheel is a rest. Its angular velocity increases uniformly and becomes `80 rad s^(-1)` after 5 s. The total angular displacement is
View SolutionA rigid body rotates about a fixed axis with variable angular velocity equal to (a - bt) at time t where a and b are constants. The angle through which it rotates before it comes to rest is
View SolutionA wheel is rotating at the rate of `33 "rev min"^(-1)`. If it comes to stop in 20 s. Then, the angular retardation will be
View SolutionA wheel is rotating at 900 rpm about its axis. When power is cut off it comes to rest in 1 min. The angular retardation in `rad s^(-2)` is
View SolutionA wheel is subjected to uniform angular acceleration about its axis. Initially, its angular velocity is zero. In the first `2 sec`, it rotates through an angle `theta_(1)`, in the next `2 sec`, it rotates through an angle `theta_(2)`. The ratio of `theta_(2)//theta_(1)` is
View SolutionThe motor of an engine is rotating about its axis with an angular velocity of 100 rev/minute. It comes to rest in 15 s, after being switched off. Assuming constant angular deceleration, calculate the number of revolutions made by it before coming to rest.
View SolutionLet `vecF` be a force acting on a particle having positon vector `vecr. Let vectau` be the torque of this force about the origin then
View SolutionA particle of mass 5 g is moving with a uniform speed of `3 sqrt(2) "cm s"^(-1)` in the XY-plane along the line `y = 2 sqrt(5)` cm. The magnitude of its angular momentum about the origin in `"g-cm"^(2) s^(-1)` is
View SolutionA particle of mass `m` is moving in yz-plane with a unifrom velocity `v` with its trajectory running parallel to +ve y-axis and intersecting z-axis at `z = a` Fig. The change in its angular momentum about the origin as it bounces elastically from a wall at y = constant is :

View SolutionA particle of mass `m=5` units is moving with a uniform speed `v = 3 sqrt(2)` units in the XY-plane along the `y=x+4`. The magnitude of the angular momentum about origin is
View SolutionA particle of mass `2 kg` located at the position `(hat i+ hat k) m` has a velocity `2(+ hat i- hat j + hat k) m//s`. Its angular momentum about `z-`axis in `kg-m^(2)//s` is :
View SolutionA particle of mass m is projected with velocity v moving at an angle of `45^(@)` with horizontal. The magnitude of angular momentum of projectile about point of projection when particle is at maximum height, is
View SolutionA sphere of mass `M` rolls without slipping on rough surface with centre of mass has constant speed `v_0`. If its radius is R`, then the angular momentum of the sphere about the point of contact is.
View SolutionA constant torque of `1000 N-m` turns a wheel of moment of inertia `200 kg-m^2` about an axis through its centre. Its angular velocity after `3` seconds is.
View SolutionA Merry -go-round, made of a ring-like plarfrom of radius `R and mass M`, is revolving with angular speed `omega`. A person of mass `M` is standing on it. At one instant, the person jumps off the round, radially awaay from the centre of the round (as see from the round). The speed of the round after wards is
View SolutionA flywheel having a radius of gyration of 2m and mass 10 kg rotates at an angular speed of `5 rad s^(-1)` about an axis perpendicular to it through its centre. The kinetic energy of rotation is
View SolutionA flywheel is in the form of a uniform circular disc of radius `1 m` and mass `2 kg`. The work which must be done on it to increase its frequency of rotation from `5` to `10 rev//s` is approximately
View SolutionA rod is placed along the line,`y=2x` with its centre at origin. The moment of inertia of the rod is maximum about.
View SolutionThe ratio of the radii of gyration of a circular disc and a circular ring of the same radii about a tangential axis perpendicular to plane of disc or ring is
View SolutionLet `I_(A) and I_(B)` be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of massof the body but B does not. Choose the correct option.
View SolutionThe ratio of the radii of gyration of a hollow sphere and a solid sphere of the same radii about a tangential axis
View SolutionA square lamina is as shown in figure. The moment of inertia of the frame about the three axes as shown in figure `I_(1),I_(2) and I_(3)` respectively. Select the correct alternative.
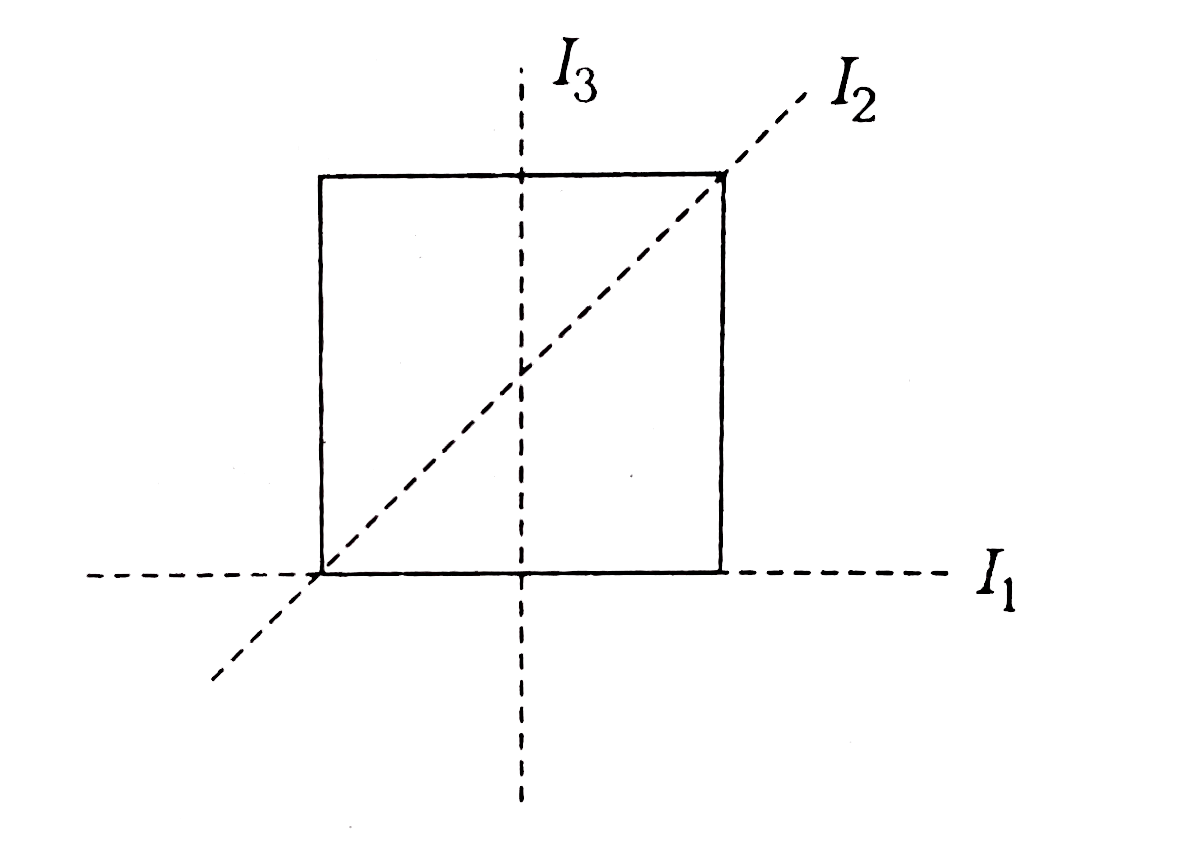
View SolutionThe ratio of the radii of gyration of a circular disc about a tangential axis in the plane of the disc and a circular ring of the same radius about a tangential axis in the plane of the ring is
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity `omega` . Another disc of same dimensions but of mass `(1)/(4)` M is placed gently on the first disc co-axially. The angular velocity of the system is
View SolutionA ring is rolling on an inclined plane. The ratio of the linear and rotational kinetic energies will be?
View SolutionA wheel of bicycle is rolling without slipping on a level road. The velocity of the centre of mass is `v_(CM)`, then true statement is

View SolutionA disc is rolling without slipping on a horizontal surface with C, as its centre and Q and P the two points equidistant from C. Let `v_(P),v_(Q) and v_(C)` be the magnitudes of velocities of point P,Q and C respectively, then

View SolutionA rigid body rotates with an angular momentum L. If its rotational kinetic energy is made 4 times, its angular momentum will become
View SolutionA ring and a disc of different masses are rotating with the same kinetic energy. If we apply a retarding torque `tau` on the ring, it stops after making n revolution. After how many revolutions will the disc stop, if the retarding torque on it is also `tau` ?
View SolutionWork done by friction in case of pure rolling
View SolutionForces are applied on a wheel of radius 20 cm as shown in the figure. The torque produced by the forces 4 N at A, 8N at B, 6 N at C and 9N at D at angles indicated is

View SolutionABC is an equilateral triangle with `O` as its centre. `F_(1), F_(2)` and `F_(3)` represent three forces acting along the sides `AB, BC` and `AC` respectively. If the total about `O` is zero, then the magnitude of `F_(3)` is

View SolutionThe figure shows the angular velocity versus time graph of a flywheel. The angle, in radians through which the flywheel turns during 25 s is
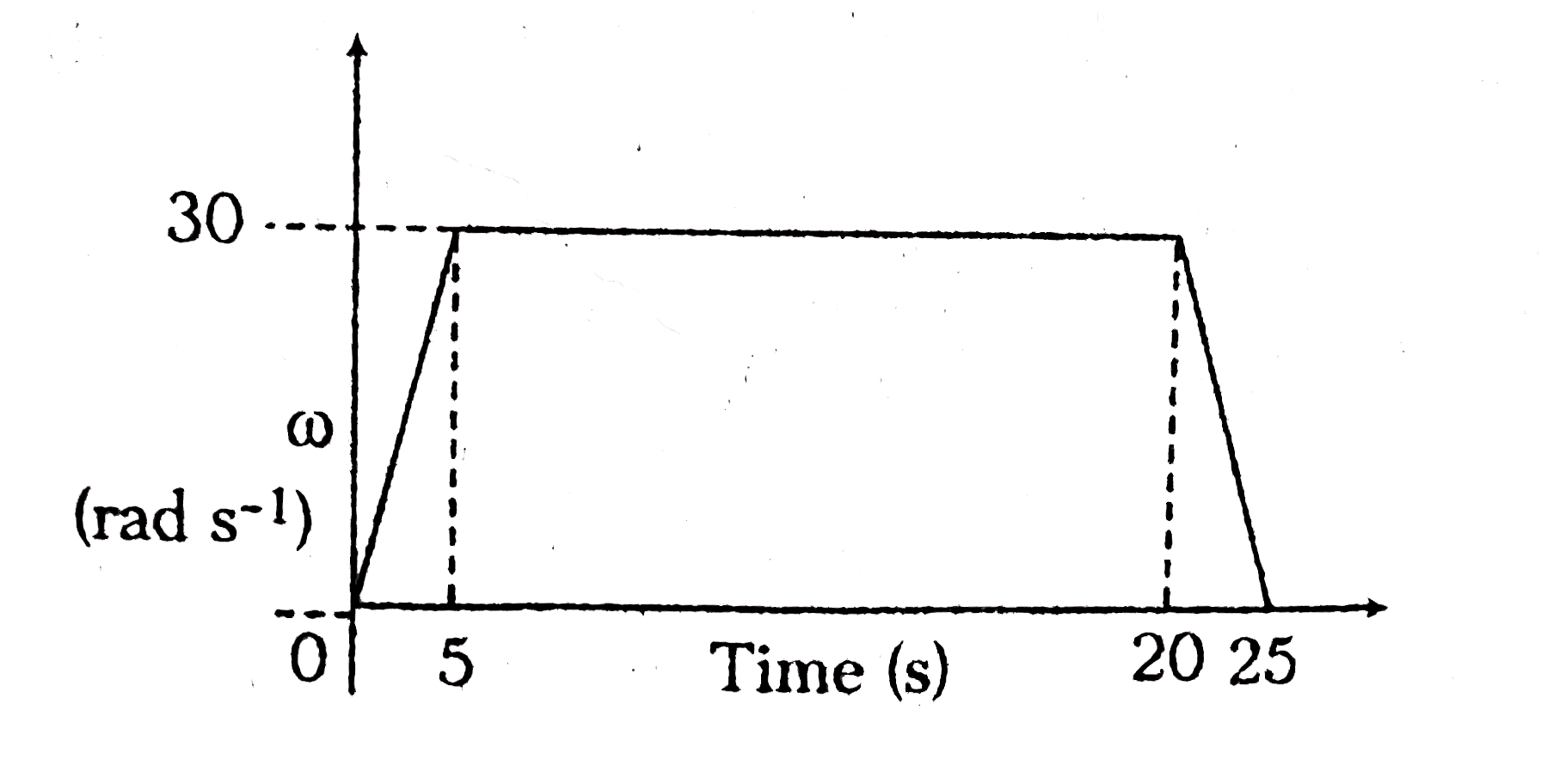
View SolutionA table fan, rotating at a speed of 2400 rpm, is switched off and the resulting variation of the rpm with time is shown in the figure. The total number of revolutions of the fan before it comes to rest is

View SolutionA sphere can roll on a surface inclined at an angle `theta` if the frictioni coefficient is more than `2/7 g tantheta`. Suppose the friction coefficient ils `1/7gtantheta`.If a sphre is released from reest on the incline.
View SolutionIf a disc of mass m and radius r is reshaped into a ring of radius`2r`, the mass remining the same, the radius of gyration about centrodal axis perpendicular to plane goes up by a factor of
View SolutionA disc of mass m and radius R is rolling on horizontal ground with linear velocity v. What is the angular momentum of the disc about an axis passing through bottommost point and perpendicular to the plane of motion ?
View SolutionTwo discs have same mass and thickness. Their materials are of densities `d_(1) and d_(2)`. The ratio of their moments of inertia about an axis passing through the centre and perpendicular to the plane is
View SolutionA ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is `k`. IF radius of the ball be `R`, then the fraction of total energy associated with its rotational energy will be
View SolutionThe speed of a homogenous solid sphere after rolling down an inclined plane of vertical height h, from rest without sliding is
View SolutionConsider three solid spheres, sphere (i) has radius r and mass m, sphere (ii) has radius r and mass 3 m, sphere (iii) has radius 3r and mass m, All can be placed at the same point on the same inclined plane, where they will roll without slipping to the bottom, If allowed to roll down the incline, then at the bottom of the incline
View SolutionThe moment of inertia of a system of four rods, each of length l and mass m, about the axis shown is:

View Solutionthe density of a non-uniform rod of length 1 m is given by `rho(x)=a(1+bx^(2))` where ,a and b are constants and `0lexle1,` the centre of mass of the rod will be at.
View SolutionABC is right angled triangular plane of uniform thickness The sides are such that AB gt BC as sshown in figure `I_(1),I_(2),I_(3)` are moments of inertia about AB, BC and AC, respectively.Then which of the following relations is correct?
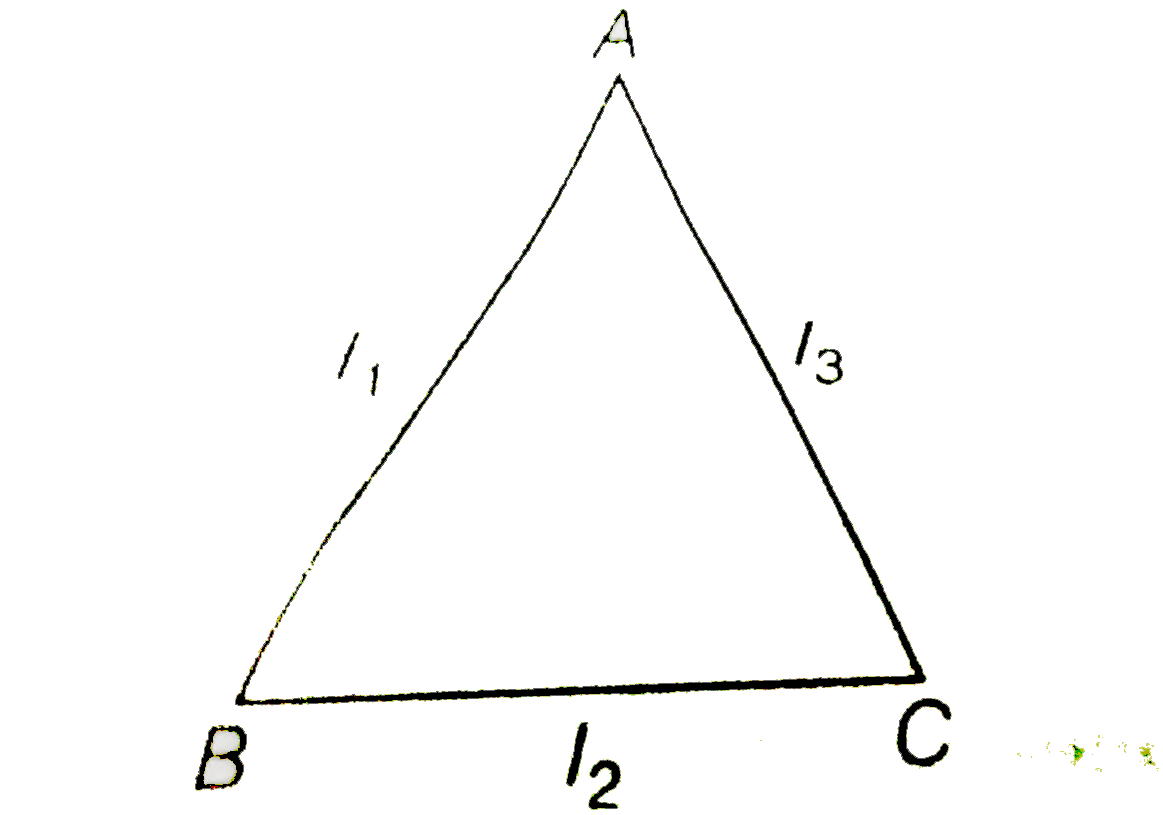
View SolutionThe moment of inertia of a cube of mass m and side a about one of its edges is equal to
View SolutionTwo uniform, thin identical rods each of mass M and length `l` are joined together to form a cross. What will be the moment of inertia of the cross about an axis passing through the point at which the two rods are joined and perpendicular to the plane of the cross ?
View SolutionFigure represents the moment of inertia of the solid sphere about an axis parallel to the diameter of the solid sphere and at a distance x from t. Which one of the following represents the variations of `I` with `x` ?
View SolutionA heavy particle is projected with a velocity at an angle with the horizontal into the uniform gravitational field. The slope of the trajectory of the particle varies as
View SolutionIf a sphere of mass `m` moving with velocity `u` collides with another identical sphere at rest on a frictionless surface, then which of the following is correct ?
View SolutionA uniform rod of mass `2 kg` and length `1 m` lies on a smooth horizontal plane. A particle of mass 1 kg moving at a speed of `2ms^-1` perpendicular to the length of the rod strikes it at a distance `(1)/(4)` m from the centre and stops . Find the angular velocity of the rod about its centre just after the collision (in rad/s)
View SolutionA particle 'P' is moving in a circle of radius 'a' with a uniform speed 'u' 'C' is the centre of the circle and AB is a diameter. The angular velocity of P about A and C are in the ratio
View SolutionA uniform round object of mass `M`, radius `R` and moment of inertia about its centre of mass `I_(cm)` has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the celling and the object is released from rest. Find the acceleration of centre of the object and tension n the string. [ Take `(I_(cm))/(MR^(2))=k`]
View SolutionA wheel comprises a ring of radius R and mass M and three spokes of mass m each. The moment of inertia of the wheel about its axis is

View Solution
A square is made by joining four rods each of mass `M` and length `L`. Its moment of inertia about an axis PQ, in its plane and passing through one one of its corner is
View SolutionA solid homogeneous sphere is moving on a rough horizontal surface, partily rolling and partially sliding. During this kind of motion of the sphere.
View SolutionA sphere cannot roll on
View SolutionA thin bar of mass `m` and length `l` is free to rotate about a fixed horizontal axis through a point at its end.The bar is brought to a horizontal position. `(theta = 90^(@))` and then released. The angular velocity when it reaches the lowest point is
View SolutionA disc is free to rotate about a smooth horizontal axis passing through its centre of mass. A particle is fixed at the top of the disc. A slight push is given to the disc and it starts rotating. During the process.

View Solution
View SolutionTwo identical satellites are moving around the Earth in circular orbits at heights 3R and R respectively where R is the radius of the Earth. The ratio of their kinetic energies is x. Find x.
View SolutionA solid sphere of mass 2 kg rolls up a `30^(@)` incline with an initial speed of `10 ms^(-1)`. The maximum height reached by the sphere is `(g = 10 ms^(-2))`
View SolutionThe figure shows a uniform rod lying along the X-axis. The locus of all the points lying on the XY-plane, about which the moment of inertia of the rod is same as that about O is
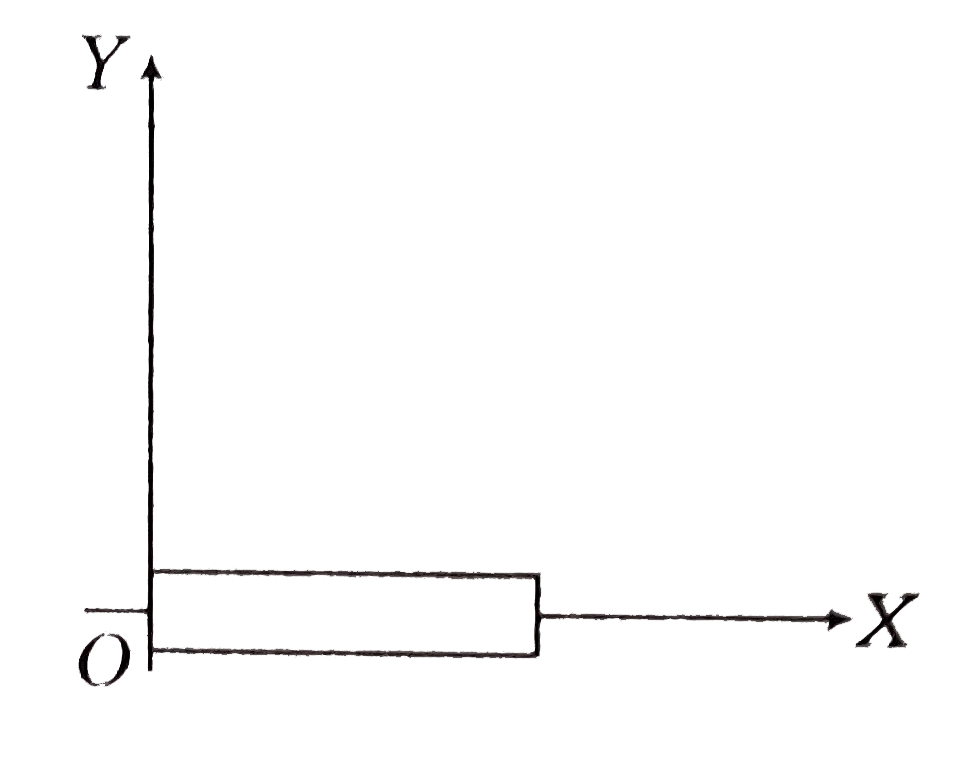
View SolutionA cord is wound around the circumference of wheel of radius r. The axis of the wheel is horizontal and `MI` is `I`. A weight mg is attached to the end of the cord and falls from rest. After falling through a distance h, the angular velocity of the wheel will be
View SolutionA solid sphere rolls without slipping and presses a spring of spring constant `k` as shown in figure. Then, the compression in the spring will be
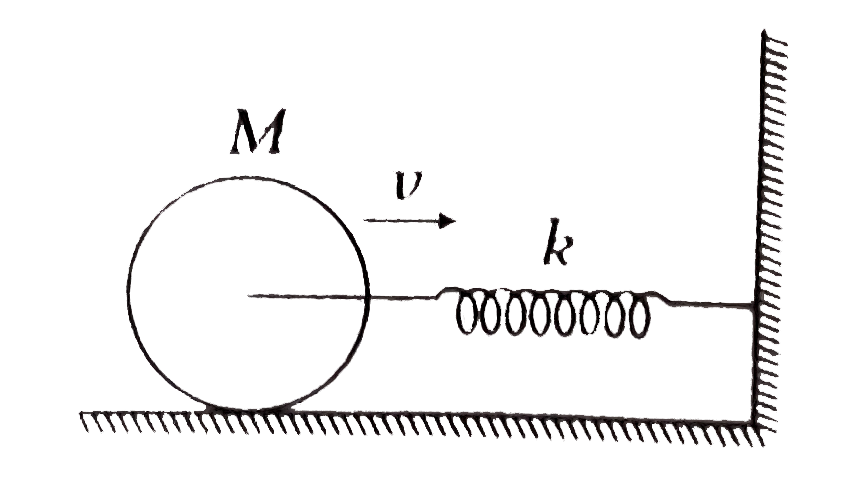
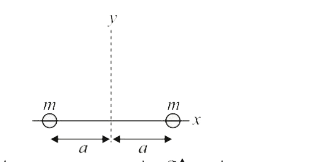
View SolutionTwo identical spherical balls, each of mass m, are placed as shown in figure. Plot the variation of g(gravitation intensity) along the x-axis due to both the masses.
View Solution
System is shown in the figure. Velocity of sphere A is 9 `(m)/(s)`. Find the speed of sphere B.
View SolutionTwo uniform spheres A (Hollow) and B (solid) of same radius R (
View Solution
(A) Chapter Exercises questions and complete solutions for chapter ROTATION of DC PANDEY ENGLISH of Class 11