Complete Solutions to Example of chapter THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES |
| DC PANDEY NEET | Example |
| Number Of Questions | 54 |
| Academic Year | 2023-24 |
Express a temperature of `60^@ F` in degrees Celsius and in kelvin.
View SolutionThe temperature of an iron piece is heated from `30^@ C "to" 90^@ C`. What is the change in its temperature on the fahrenheit scale and on the kelvin scale?
View SolutionOn a new scale of temperature (which is linear) and called the `W` scale. The freezing and boiling points of water are `39^(@)W` and `239^(@)W` respectively. What will be the temperature on the new scale, corresponding to a temperature of `39^(@)C` on the Celsius scale?
View SolutionAn arbitrary scale has the ice point at `-20^(@)` and the steam point at `180^(@)`. When the thermometer reads `5^(@)`, then find the read of centigrade thermometer.
View SolutionA faulty thermometer has its fixed points marked as `5^(@)` and `95^(@)`. The temperature of a bady as measured by the faulty therature is `59^(@)`. Find the correct temperature of the body on Celsisus scale.
View SolutionThe steam point and the ice point of a mercury thermometer are marked as `80^@ and 10^@`. At what temperature on centigrade scale the reading of this thermometer will be `59^@` ?
View SolutionThe pressures of the gas filled in the bulb of a constant volume gas thermometer are `66` cm and `88` cm of mercury column at `0^(@)C` and `100^(@)C` respectively. When its bulb is immersed in a liquid placed in a vessel, its pressure is `82.5` cm of mercury column. Calculate the temperature of the liquid.
View SolutionThe following observation were recorded on a platinum resistance thermometer. Resistance at melting point of ice is `=3.70 Omega,` resistance at boiling point of water at normal pressure is`=4.71 Omega,` and resistance at `t^(@)C=5.29Omega.` Calculate
Temperature coefficient of resistance of platinum.
Value of temperature t.
View SolutionA steel rular exactly `20 cm` long is graduated to give correct measurements at `20^@C`.
(a) Will it give readings that are too long or too short at lower temperatures?
(b) What will be that actual length of the rular when it is used in the desert at a temperature of `40^@ C` ? `alpha_(steel) = 1.2 xx 10^-5(.^@ C)^-1` .
View SolutionThe length of steel rod exceeds that of a brass rod by 5 cm. If the difference in their lengths remains same at all temperature, then the length of brass rod will be: (`alpha` for iron and brass are `12xx10^(-6)//^(@)C` and `18xx10^(-6)//^(@)C`, respectively)
View SolutionA metal ball having a diameter of `0.4` m is heated from `273` to `360 K.` If the coefficient of areal expansion of the material of the ball is `0.000034 K^(-1)`, then determine the increase in surface area of the ball.
View SolutionOn heating a glass block of `10,000 cm^(3)` from `25^(@)C` to `40^(@)C`, its volume increase by `4cm^(3)`. Calculate coefficient of linear expansion of glass.
View SolutionThe volume of mercury in the bulb of thermometer is `10^(-6) m^(3)`. The area of cross-section of the capillary tube is `2 xx 10^(-7) m^(2)`. If the temperature is raised by `100^(0)C`, the increase in the length of the mercury column is `(gamma_(Hg) = 18 xx 10^(-5//@)C)`
View SolutionA clock with an iron pendulum keeps correct time at `20^(@)C`. How much time will it lose or gain in a day if the temperature changes to `40^(@)C`. Thermal coefficient of liner expansion `alpha = 0.000012 per^(@)C`.
View SolutionA second's pendulum clock has a steel wire. The clock is calibrated at `20^@ C`. How much time does the clock lose or gain in one week when the temperature is increased to `30^@ C` ? `alpha_(steel) = 1.2 xx 10^(-5).^@C^(-1)`.
View SolutionAn aluminum cylinder `10` cm long with a cross section area of `20cm^2` is used as a spacer between two steel walls. At `17.2^(@)C` it just slips in between the walls. When it warms to `22.3^(@)C` calculate the stress in the cylinder and the total force it exerts on each wall, assuming that the walls are perfectly rigid and a constant distance apart.
View SolutionA non-conductiong body floats in a liquid at `25^(@)C` with `1//3` of its volume immersed in the liquid. When liquid temperature is increased to `105^(@)C,` `1//2` of body's volume is immersed is the liquid. Then, find the coefficient of real expansion of the liqquid (neglecting the expansion of container of the liquid) .
View SolutionThe coefficient of apparent expansion of a liquid when determined using two different vessle A and B are `gamma_(1)` and `gamma_(2,)` respectily. If the coefficient of linerar expansion of vesel A is `alpha.` Find the coefficient of linear expension of the vessel B.
View SolutionA glass vessel of volume `V_(o)` is completed filled with volume of the liquid will overflow? Cofficient of linear expansion of gass =`alpha` and coefficient of volume expension of the liquid =`gamma_(l)`
View SolutionAssume that one early morning when the temperature is `10^(@)C` a driver of an automobile gets his gasoline tank which is made of steel, filled with `75` L of gasoline, which is also at `10^(@)C` Durign the day, the temperature rises at `30^(@)C` how much gasoline will overflow ?
(Given, `alpha` for steel = `1.2 xx 10^(-5)"^(@) C^(-1),gamma` for gasoline `= 9.5 xx 10^(-4)"^(@)C)`
View SolutionAssume that one early morning when the temperature is `10^(@)C` a driver of an automobile gets his gasoline tank which is made of steel, filled with `75` L of gasoline, which is also at `10^(@)C` Durign the day, the temperature rises at `30^(@)C` how much gasoline will overflow ?
(Given, `alpha` for steel = `1.2 xx 10^(-5)"^(@) C^(-1),gamma` for gasoline `= 9.5 xx 10^(-4)"^(@)C)`
View SolutionA sphere of diameter 7.0 cm and mass 266.5 g float in a bath of liquid. As the temperature is raised, the sphere begins to sink at a temperature of `35^0 C`. If the density of liquid is `1.527 g cm^(-3)` at `0^o C`, find the coefficient of cubical expansion of the liquid. Neglect the expansion of the sphere.
View SolutionThe coefficient of volume expansion of glycerin is `49xx 10^(–5) K^(–1)`. What is the fractional change in its density for a `30^(@)C` rise in temperature ?
View SolutionIf masses of all molecule of a gas are halved and their speed doubled then the ratio of initial and final pressure will be
View SolutionOxygen is filled in a closed metal jar of volume `1.0xx10^(-3)m^(3)` at a pressure of `1.5xx10^(5)Pa.` and temperature `400K`. The jar has a small leak in it. The atmospheric pressure is `1.0xx10^(5)Pa` and the atmospheric temperature is `300K`. Find the mass of the gas that leaks out by time the pressure and the temperature inside the jar equalise with the surrounding.
View SolutionThe volume thermal expansion coefficient of an ideal gas at constant pressure is
View SolutionFind the average speed of nitrogen molecules at `25^(@)C.`
View SolutionIn a container, two gases neon and argon are filled. Find the ratio of the root mean square of the molecules of the two gases. `M_(Ne) = 20.0 mu` and `M_(Ar) = 39.9 mu.` The temperature of the system is `30^(@)C.`
View SolutionWhat is rms velocity of `O_(2)` gas at `127^(@)C.` ? The molecular weight of oxygen is `32.`
View SolutionCalculate the rms velocity of oxygen molecules at S.T.P. The molecular weight of oxygen is 32.
View SolutionThe molecules of a given mass of a gas have root mean square speeds of `100 ms^(-1) "at " 27^(@)C` and 1.00 atmospheric pressure. What will be the root mean square speeds of the molecules of the gas at `127^(@)C` and 2.0 atmospheric pressure?
View SolutionCalculate the root mean square, average and most probable speeds of oxygen molecules at `27^(@)C.`
View SolutionAt what temperarture, the kinetic energy of a gas molecule is half of the value at `27^(@)C.` ?
View SolutionProve that the pressure of an ideal gas is numerically equal to two third of the mean translational kinetic energy per unit volume of the gas.
View SolutionA balloon has 5.0 g mole of helium at `7^(@)C` Calculate
(a) the number of atoms of helium in the balloon,
(b) the total internal energy of the system.
View SolutionA tank used for filling helium balloons has a volume of `0 .3 m^3` and contains (2.0) mol of helium gas at `20 .0^@ C`. Assuming that the helium behaves like an ideal gas.
(a) What is the total translational kinetic energy of the molecules of the gas ?
(b) What is the average kinetic energy per molecule ?
View SolutionCalculate the ratio of the mean free path of molecules of two gases in the ratio of the numbers density per `cm^(3)` of the gases is `5:3` and the ratio of the diameters of the molecules of the gases is `4:5`
View SolutionFor a molecule of an ideal gas `n=3xx10^(8)cm^(-3)` and mean free path is `10^(-2)` cm. Calculate the diameter of the molecule.
View SolutionA gas at `27^@ C` in a cylinder has a volume of 4 litre and pressure `100 Nm^-2`.
(i) Gas is first compressed at constant temperature so that the pressure is `150 Nm^-2` . Calculate the change in volume.
(ii) It is then heated at constant volume so that temperature becomes `127^@ C`. Calculate the new pressure.
View SolutionThe pressure of a given mass of a gas filled in a vessel of volume V at constant temperature is reduced to `1//3` rd of its initial value. Calculate the percentage change in its volume.
View SolutionAir is filled in a container of `333K.` Calculate the tempeture upto which it should be heated so that `1//3 rd of air may escope out of th vessel.
View SolutionIf pressure of a gas contained in a closed vessel is increased by `0.4%` when heated by `1^(@)C`, the initial temperature must be
View SolutionOne mole each of hydrogen, oxygen and nitrogen are mixed in a close container of volume `10` L and temperature `27^(@)C.` Calculate the pressure exerated by the mixture. `(R=.314Jmol^(-1)K^(-1))`
View Solution`4 g` hydrogen is mixed with 11.2 litre of He at (STP) in a container of volume 20 litre. If the final temperature is `300 K`, find the pressure.
View SolutionIf pressure of `CO_(2)` (real gas ) in a container is given by `P = (RT)/(2V - b) - (a)/(4b^(2))`, then mass of the gas in container is a) 11g b) 22g c) 33g d) 44g
View SolutionThe `p-V` diagrams of same mass of a gas are drawn at two different temperatues `T_(1)` and `T_(2)` Explain whether `T_(1)gtT_(2)` or `T_(2)gtT_(1).`
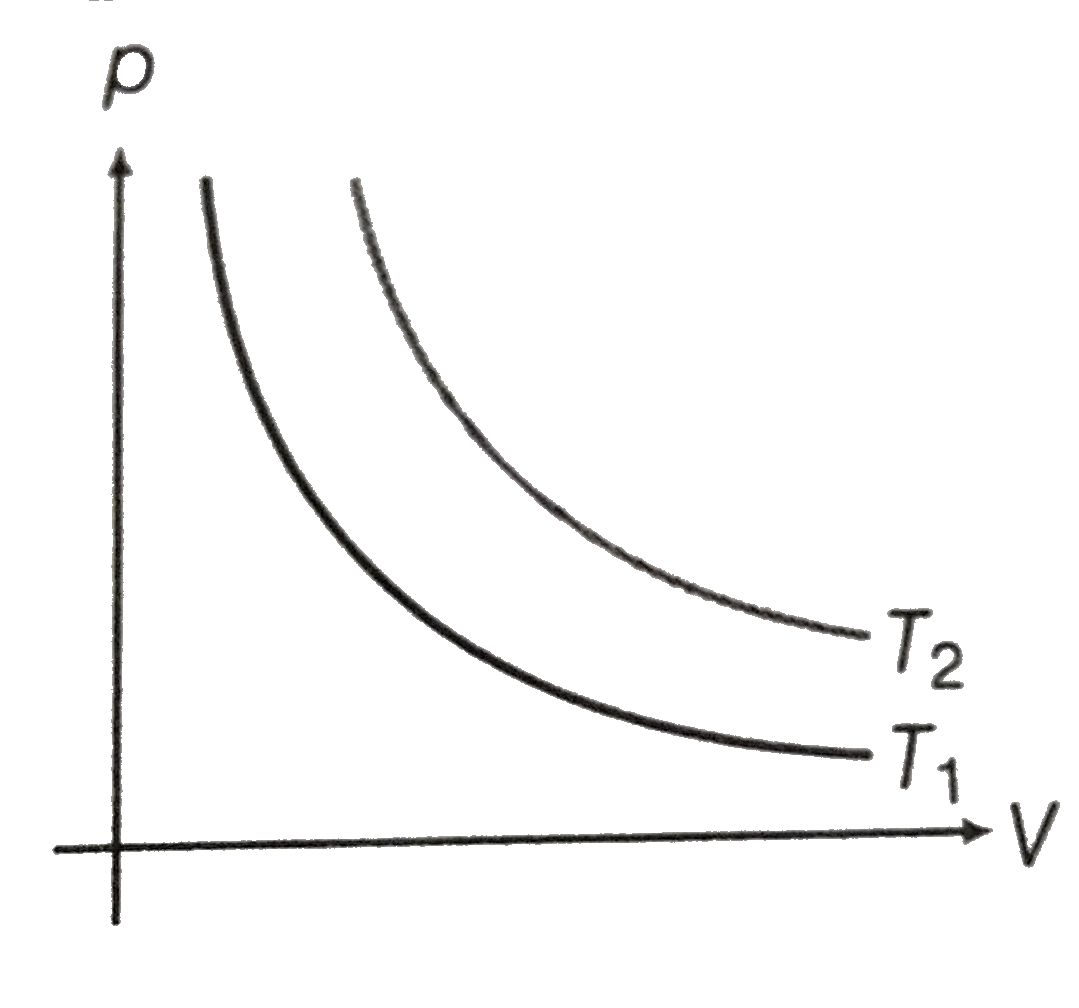
View SolutionThe `p -V` diagram of two different masses `m_(1)` and `m_(2)` are drawn (as shown) at constant temperature `(T)`.
View SolutionThe `p-T` graph for the given mass of an ideal gas is shown in figure. What inference can be drawn regarding the change in Volume (whtherit is constant, increasing or decreasing) ?

View SolutionCalculate the ratio of KE of molecule of oxygen and neon gas at `27^(@)C.`
View SolutionCalculate the average kinetic energy of oxygen molecule at `0^(@)`C. `(R=8.314 J mol^(-1)` `K^(-1),N_(A)`=`6.02xx10^(23))`
View SolutionFind the average kinetic energy per molecule at temperature T for an equimolar mixture of two ideal gases A and B, where A is monoatmic and B is diamtomic.
View SolutionCalculate the change in internal energy of `3 .0` mol of helium gas when its temperature is increased by `2. 0 K`.
View SolutionGiven, Avogadro's number `N = 6.02 xx 10^23` and Boltzmann's constant `k = 1.38 xx 10^-23 J//K`.
(a) Calculate the average kinetic energy of translation of the molecules of an ideal gas at `0^@ C and at 100^@ C`.
(b) Also calculate the corresponding energies per mole of the gas.
View SolutionOne mole of an ideal monoatomic gas is taken at a temperature of `300 K`. Its volume is doubled keeping its pressure constant. Find the change in internal energy.
View Solution
Example questions and complete solutions for chapter THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES of DC PANDEY ENGLISH of Class 11