Complete Solutions to Examples of chapter CALORIMETRY AND HEAT TRANSFER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CALORIMETRY AND HEAT TRANSFER |
| DC PANDEY NEET | Examples |
| Number Of Questions | 43 |
| Academic Year | 2023-24 |
When 400 J of heat are added to a 0.1 kg sample of metal, its temperature increase by `20(@)`C. What isthe specific heat of the metal?
View SolutionA 10 kW drilling machine is used to drill a bore in a small aluminium block of mass 8.0 kg. How much is the rise in temperature of the block in 2.5 minutes, assuming 50% of power is used up in heating the machine itself or lost to the surroundings. Specific heat of aluminium `= 0.91 J g^(–1) K^(–1)`.
View SolutionA geyser heats water flowing at the rate of 30 litre per minute from `27 ^(@)C` to `77^(@)C` If the geyser operates on a gas bomer, what is the rate of consumption of the fuel if its heat of combustion is `4.0 xx 10 ^(4) xx J //g?`
View Solution0.64 g of oxygen is kept ini a rigid container and is heated. Find the amount of heat required to raise the temperature from `20^(@)` to `30^(@)` C. The molar heat capacity of oxygen at constant volume is `20JK^(-1)mol^(-1)`
View SolutionA certain substance has a mass of 50/gmol. When 300 J of heat is added to 25 g of sample of this material, its tempertuare rises from 25 to `45^(@)`C. Calcualte (i) thermal capacity.. (ii) Specific heat and (iii) molar heat capacity of the sample.
View Solution10 g of water at `70^@C` is mixed with 5 g of water at `30^@C`. Find the temperature of the mixture in equilibrium. Specific heat of water is `1 cal//g.^@C`.
View SolutionTwo liquids A and B are at `30^@C` and `20^@C`, respectively When they are mixied in equal masses, the temperature of the mixture is found to be `26^@C`. The ratio of their specific heat is
View SolutionThe temperature of equal masses of three different liquids A, B and C are `12^@C, 19^@C and 28^@C` respectively. The temperature when A and B are mixed is `16^@C` and when B and C are mixed is `23^@C`. The temperature when A and C are mixed is
View SolutionA piece of iron of mass `100g` is kept inside a furnace for a long time put in a calorimeter of water equivalent `10g` containing `240g` of water at `20^(@)C` The mixture attains an equilibrium temperature of `60^(@)C` Find the temperature of the furnace specific heat capacity of iron `= 470J kg^(-1)C^(-1)`
View SolutionAt 1 atmospheric pressure, 1.000 g of water having a volume of `1.000 cm^3` becomes 1671 `cm^3` of steam when boiled. The heat of vaporization of water at 1 atmosphere is `539 cal//g` . What is the change in internal energy during the process ?
View SolutionFind the quantity of heat required to convert 40 g of ice at `-20^(@)`C into water at `20^(@)`C. Given `L_(ice) = 0.336 xx 10^(6) J/kg.` Specific heat of ice = 2100 J/kg-K
Specific heat of water = 4200 J/kg-K
View SolutionIn a container of negligible mass 30g of steam at `100^@C` is added to 200g of water that has a temperature of `40^@C` If no heat is lost to the surroundings, what is the final temperature of the system? Also find masses of water and steam in equilibrium. Take `L_v = 539 cal//g and c_(water) = 1 cal//g.^@C.`
View Solution19 g water at `30^(@)C` and 5 g of ice at `-20^(@)C` are mixed together in a calorimeter. What is the final temperature of the mixture ? Given specific heat of ice =`0.5 cal g^(-1^@)C^(-1)` and latent heat of fusion of ice = `80 cal g^(-1)`
View Solution`5g` ice at `0^(@)C` is mixed with `5g` of steam at `100^(@)C`. What is the final temperature?
View SolutionA lead bullet penetrates into a solid object and melts Assuming that `50%` of its K.E. was used to heat it , calculate the initial speed of the bullet , The initial temp , of bullet is `27^(@)c` and its melting point is `327^(@)C` Latent heat of fasion of lead ` = 2.5 xx 10^(4) J kg^(-1)` and sp heat capacity of lead `= 125 J kg^(-1) K^(-1)`
View Solutionsuppose you want to cool 0.25 kg of cola (mostly water ), at `25^(@)C` by adding ice initially at `-20^(@)C`. How much ice should you add so that the final temperature will be `0^(@)C` with all the ice melt? Neglect the heat capacity of the container. specific heat of ice is` 2000 Jkg^(-1)K^(-1)`. [take specific heat of cola `4160 Jkg^(-1)K^(-1)`.]
View SolutionAn ice cube of mass 0.1 kg at `0^@C` is placed in an isolated container which is at `227^@C`. The specific heat s of the container varies with temperature T according to the empirical relation `s=A+BT`, where `A= 100 cal//kg.K and B = 2xx 10^-2 cal//kg.K^2`. If the final temperature of the container is `27^@C`, determine the mass of the container.
(Latent heat of fusion for water = `8xx 10^4 cal//kg`, specific heat of water `=10^3 cal//kg.K`).
View SolutionA solid material is supplied with heat at a constant rate. The temperature of the material is changing with the heat input as shown in the graph in figure. Study the graph carefully and answer the following questions:
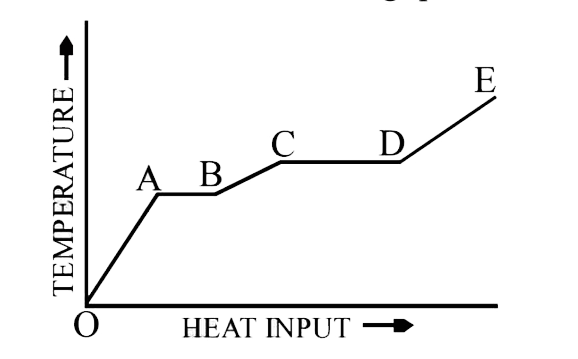
(i) What do the horizontal regions AB and CD represent?
(ii) If CD is equal to 2AB, what do you infer?
(iii) What does the slope of DE represents?
(iv) The slope of `OAgtthe` slope of `BC`. What does this indicate?
View Solution
Two bodies of equal masses are heated at a uniform rate under identical conditions. The change in temperature in the two cases in shown graphically. What are their melting points?
Find the ratio of their specific heats and latent heats.
View SolutionHow much heat is required to convert 8.0 g of ice at `-15^@C` to steam at `100^@C`? (Given, `c_(ice) = 0.53 cal//g.^@C, L_f = 80 cal//g and L_v = 539 cal//g, `
and `c_(water) = 1 cal//g.^@C)` .
View Solution100 g ice at `0^(@)C ` is mixed with 10 g steam at `100^(@)C ` . Find the final temperature.
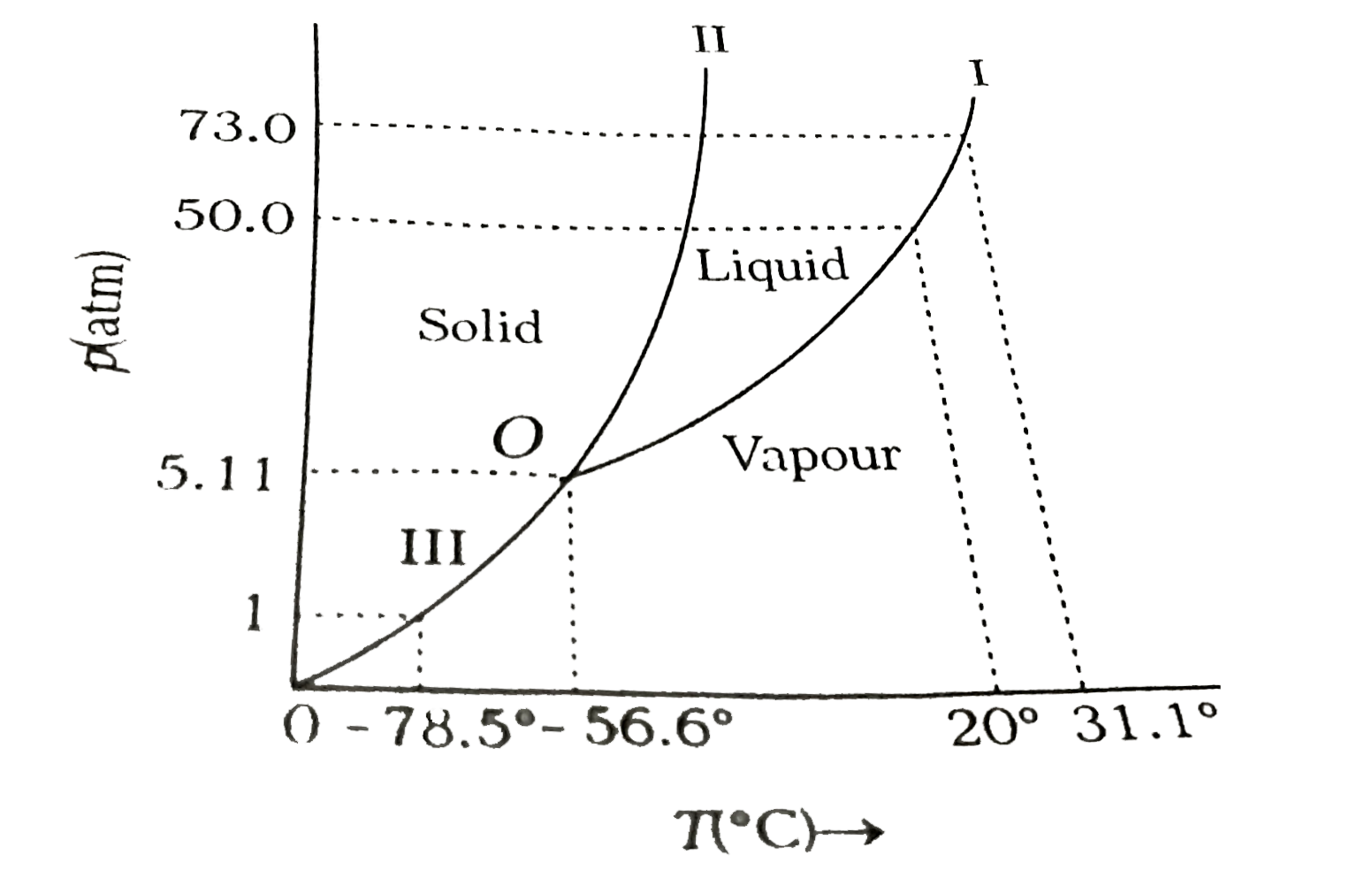
View SolutionAnswer the following questions based on the p-T phase diagram of carbon dioxide as shown in the figure .
(i) At what temperature and pressure can the solid , liquid and vapour phases of `C0_(2)` co-exist in equilibrium?
(ii) What is the effect of decrease of pressure on the fusion and boiling point of `C0_(2)` ?
(iii) What are the critical temperature and pressure for `C0_(2)` ? what is their significance ?
(iv) Is `C0_(2)` solid , liquid, or gas at (a) `-70^(@)C `under 1 atm (b) `-60^(@)C` under 10 atm (c) `15^(@)C` under 56 atm ?
View SolutionThickness of ice on a lake is 5 cm and the temperature of air is `-20^(@)C` . If the rate of cooling of water inside the lake be 20000 cal `min^(-1)` through each square metre surface , find K for ice .
View SolutionOne end of a copper rod of length 1 m and area of cross - section `400 xx 10^-4 m^2` is maintained at `100^@C`. At the other end of the rod ice is kept at `0^@C`. Neglecting the loss of heat from the surrounding, find the mass of ice melted in 1h. Given, `K_(Cu) = 401 W//m.K and L_f = 3.35 xx 10^5 J//kg.`
View SolutionAn iron boiler is 1 cm thick and has a heating area `2.5 m^(2)`. The two surface of the boiler are at `230^(@)C` and `100^(@)C` respectively. If the latent heat of the steam is `540 kcal kg^(-1)` and thermal conductivity of iron is `1.6xx10^(-2)K cal s^(-1) m^(-1)K^(-1)`, then how much water will be evaporated into steam per minute ?
View SolutionA copper rod 2 m long has a circular cross-section of radius 1 cm. One end is kept at `100^@C` and the other at `0^@C`. The surface is insulated so that negligible heat is lost through the surface. In steady state, find
(a) the thermal resistance of the bar
(b) the thermal current H
(c) the temperature gradient `(dT)/(dx)` and
(d) the temperature at a distance 25 cm from the hot end.
Thermal conductivity of copper is 401 `W//m.K.`
View SolutionThree rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are `T_(1) and T_(2) (T_(1)gtT_(2))` find the rate of heat transfer H.

View SolutionA composite slab is prepared by pasting two plates of thickness `L_(1)` and `L_(2)` and thermal conductivities `K_(1)` and `K_(2)` . The slab have equal cross-sectional area. Find the equivalent conductivity of the composite slab.
View SolutionThree bars of equal lengths and equal area of cross-section are connected in series fig. their thermal conducitives are in the ratio `2:3:4`. If at the steady state the open ends of the first and the last bars are at temperature `200^(@)C` and `20^(@)C` respectively, find the temperature of both the junctions.
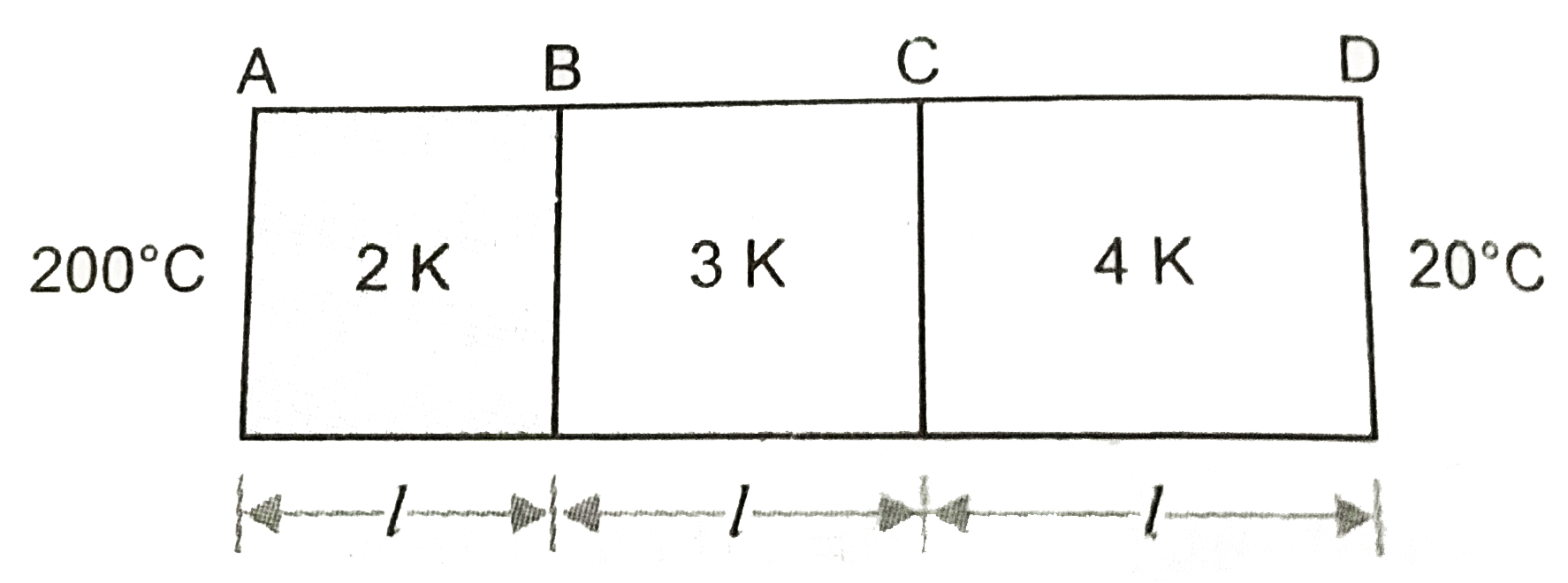 .
.
View SolutionAn iron bar (`L_(1) = 0.1 m, A_(1) = 0.02 m^(2) , K_(1) = 79 Wm^(-1) K^(-1)`) and a brass bar `(L_(2)=0.1 m , A_(2) = 0.02 m^(2), K_(2) = 109 Wm^(-1)K^(-1)`) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the junction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar.
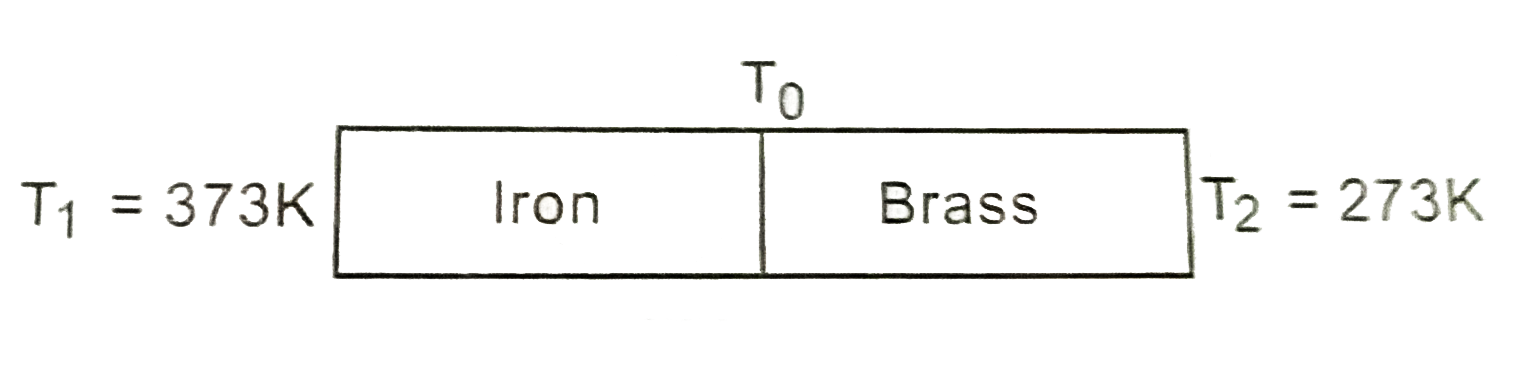 .
.
View SolutionAn aluminium rod and copper rod of equal length `1 m` and cross-sectional area `1 cm^(2)` are welded as shown. `K_(A1) = 200 W//m^(@)C, K_(Cu) = 400 W//m^(@)C`. Find heat current


View SolutionTwo metal cubes with 3 cm- edges of copper and aluminium are arranged as shown in figure. Find
(a)the total thermal current from one reservoir to the other
(b) the ratio of the thermal current carried by the copper cube to that carried by the aluminium cube. Thermal conductivity of copper is 401 `W//m.K` and that of aluminium id 237 `W//m.K` .

View SolutionThree identical rods have been joined at a junction to make it a Y shape structure. If two free ends are maintained at `45^(@)C` and the end is at `0^(@)C`, then what is the junction temperature T?
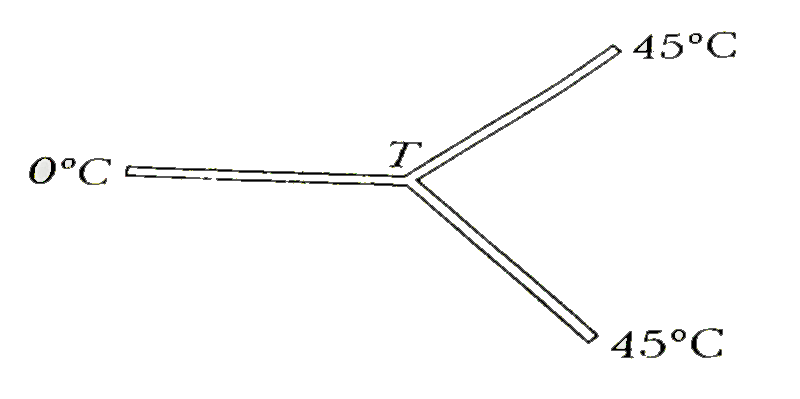
View SolutionA steel bar 10.0 cm long is welded end to end to a copper bar 20.0 cm long. Both bars are insulated perfectly on their sides . Each bar has a separate cross-section, 2.00 cm on a side . The free end of the steel bar is maintained at `100^(@)C` by placing it in contact with steam and free end of the copper bar is maintained at `0^(@)C` by placing it in contact with ice . find the temperature at the junction of the two bars and the total rate of heat flow . thermal conductivity of steel `= 50.2 Wm^(-1)K^(-1)`.thermal conductivity of copper `=385 Wm^(-1)K^(-1)`.
View SolutionA cylinder of radius `R` made of a material of thermal conductivity `K_(1)` is surrounded by cylindrical shell of inner radius `R` and outer radius `2R` made of a material of thermal con-ductivity `K_(2)` The two ends of the combined system are maintained at two differnet tem-peratures There is no loss of heat across the cylindrical surface and system is in steady state What is the effective thermal conductivity of the system
 .
.
View SolutionA black body at `227^(@)C` radiates heat at the rate of 7 cal `cm^(-2) s^(-1)`. At a temperature of `727^(@)C`, the rate of heat radiated in the same units will be
View SolutionA cubical block of mass `1.0kg` and edge `5.0cm` is heated to `227^(@)C` . It is kept in an evacuated chamber maintained at `27^(@)C` . Assming that the block emits radiation like a blackbody, find the rate at which the temperature of the block will decreases. Specific heat capacity of the material of the block is `400Jkg^(-1)K^(-1)` .
View SolutionOne end of a rod of length `20cm` is inserted in a furnace at `800K` The sides of the rod are covered with an insulating material and the other end emits radiation like a black body. The temperature of this end is `750K` in the steady state The temperature of the surrounding air is `300K` Assuming radiation to be the only important mode of energy transfer between the surrounding and the open end of the rod, find the thermal conductivity of the rod Stefan's constant `sigma = 6.0 xx 10^(-8) W m^(-2) K^(-4)` .
View SolutionA body cools in 10 min from `60^(@)`C to `40^(@)`C and to `42.5^(@)`C in 7.5 min. Find the temperature of the surroundings.
View SolutionA body cools down from `52.5^(@)`C to `47.5^(@)C` in 5 min and to `42.5^(@)`C in 7.5 min. Find the temperature of the surroundings.
View SolutionThe spectral energy distribution of the sun has maxima at 4753 `Å`. Find the temperature of a star for which spectral distribution has maxima at 10350 `Å`. [Temperature of sun is 6000 K]
View SolutionTwo bodies A and B have thermal emissivities of 0.01 and 0.81 respectively. The outer surface areas of the two bodies are same. The two bodies emit total radiant power at the same rate. The wavelength `lambda_B` corresponding to maximum spectral radiancy from B is shifted from the wavelength corresponding to maximum spectral radiancy in the radiation from A by 1.0 `mum`. If the temperature of A is 5802 K, calculate (a) the temperature of B, (b) wavelength `lambda_B`.
View SolutionWhich one of the following is `v_(m) - T` graph for perfectly black body ? `v_(m)` is the frequency of radition with maximum intensity. T is the absolute temperature
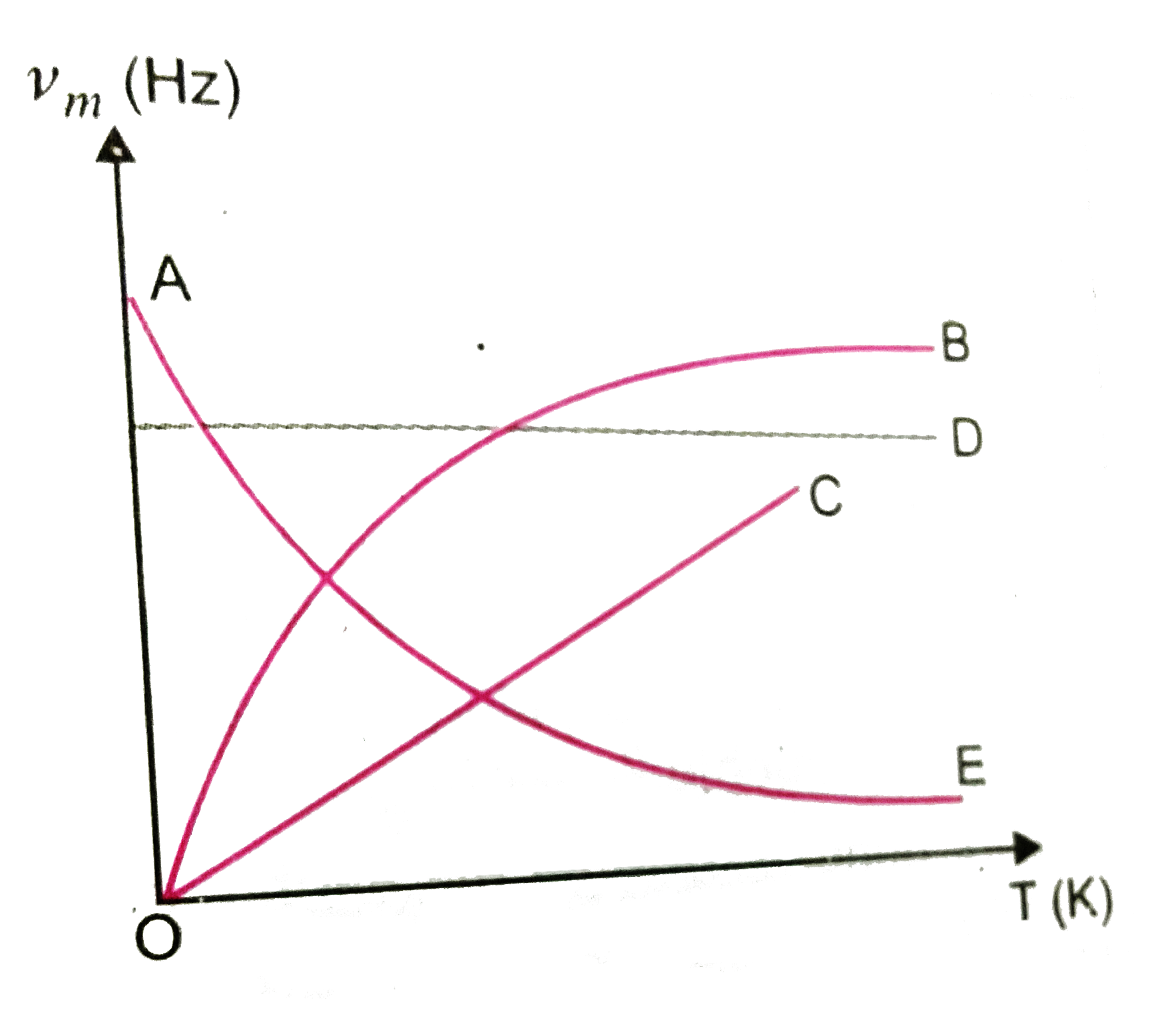
View Solution
Examples questions and complete solutions for chapter CALORIMETRY AND HEAT TRANSFER of DC PANDEY ENGLISH of Class 11