One end of a copper rod of length 1 m and area of cross - section 400×10−4m2 is maintained at 100∘C. At the other end of the rod ice is kept at 0∘C. Neglecting the loss of heat from the surrounding, find the mass of ice melted in 1h. Given, KCu=401W/m.KandLf=3.35×105J/kg.

Thermal resistance of the rod, R=lKA=1.0401(4×10−4=6.23KW−1
∴ Heat current, h=(Temperature difference)/(Thermal resistance)<br>(100-0)/6.23 = 16W<br>Heattranerred∈1h,<br>Q=Ht<br>(therefore H=Q/t)<br>Now,≤tmbethemassoficetˆme<s∈1h,then<br>m=Q/L(Q=mL)<br>=(57600/(3.35 xx 10^(5) = 0.172 kg or 172 g
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check point 16.1
10 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check point 16.2
10 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
The ends of copper rod of length 1m and area of cross section 1cm2 are maintained at 0∘C and 100∘C. At the centre of rod, there is a source of heat of 32W. The thermal conductivity of copper is 400W/mK

View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View SolutionThe left end of a copper rod (length=20cm, Area of cross section=0.2cm2) is maintained at 20∘C and the right end is maintained at 80∘C . Neglecting any loss of heat through radiation, find (a) the temperature at a point 11cm from the left end and (b) the heat current through the rod. thermal conductivity of copper =385Wm−1C−1 .
View SolutionOne end of a brass rod of length 2.0 m and cross section 1cm2 is kept in steam at 100∘C and the other end in ice at 0∘C. The lateral surface of the rod is covered by heat insulator. Determine the amount of ice melting per minute. Thermal conductivity of brass is 110W/m−K and specific latent heat of fusion of ice is 80cal/g.
View SolutionOne end of the rod of length l, thermal conductivity K and area of cross-section A is maintained at a constant temperature of 100∘C. At the other end large quantity of ice is kept at 0∘C . Due to temperature difference, heat flows from left end to right end of the rod. Due to this heat ice will start melting. Neglecting the radiation losses find the expression of rate of melting of ice.
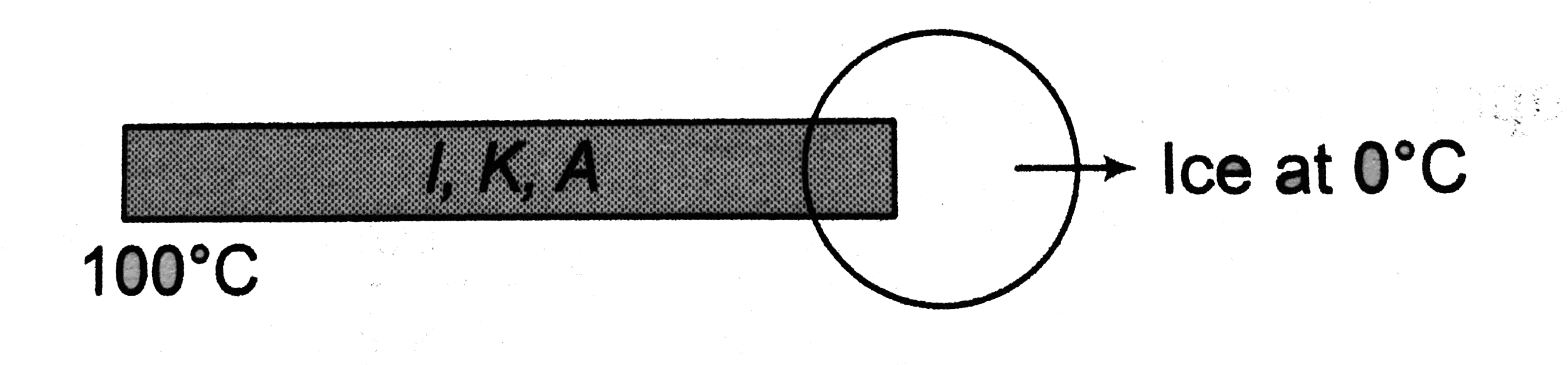 .
.
View SolutionA heat flux of 4000 J/s is to be passed through a copper rod of length 10 cm and area of cross section 100cm2. The thermal conductivity of copper is 400W/m/∘C The two ends of this rod must be kept at a temperature difference of
View SolutionA heat flux of 4000 J/s is to be passed through a copper rod of length 10 cm and area of cross section 100cm2. The thermal conductivity of copper is 400W/m/∘C The two ends of this rod must be kept at a temperature difference of
View SolutionFigure shows a steel rod joined to a brass rod. Each of the rods has length of 31cm and area of cross-section 0.20cm2. The junction is maintained at a constant temperature 50∘C and the two ends are maintained at 100∘C. The amount of heat taken out from the cold junction in 10 minutes after the steady state is reached in n×102J. Find 'n' the thermal conductivities are Ksteel=46W/m−∘C and Kbrass=109W/m−∘C.

View SolutionOne end of a copper rod of length 1.0 m and area of cross-section 10−3 is immersed in boiling water and the other end in ice. If the coefficient of thermal conductivity of copper is 92cal/m−s−.∘C and the latent heat of ice is 8×104cal/kg, then the amount of ice which will melt in one minute is
View Solution
