Complete Solutions to Level 1 Subjective of chapter WAVE MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WAVE MOTION |
| DC PANDEY | Level 1 Subjective |
| Number Of Questions | 17 |
| Academic Year | 2023-24 |
A certain transverse wave is described by
`y(x, t)=(6.50 mm) cos 2pi((x)/(28.0 cm) - (t)/(0.0360 s)).`
Determine the wave's
(a) amplitude , (b) wavelength
( c ) frequency , (d) speed of propagation and
(e) direction of propagation.
View SolutionFor the wave `y=5 sin 30pi[t-(x//240)]`, where `x and y` are in cm and `t` is in seconds, find the
(a) displacement when `t = 0` and `x = 2 cm`
(b) wavelength
( c ) velocity of the wave and
(d) frequency of the wave
View SolutionThe displacement of a wave disturbance propagating in the positive x-direction is given by
`y =(1)/(1 + x^(2))`at `t = 0` and `y =(1)/(1 +(x - 1)^(2))` at `t =2s`
where, `x` and `y` are in meter. The shape of the wave disturbance does not change during the propagation. what is the velocity of the wave?
View SolutionA travelling wave pulse is given by `y = (10)/(5 + (x + 2t)^(2))`
Here, `x and y` are in meter and `t` in second. In which direction and with what velocity is the pulse propagation. What is the ampitude of pulse?
View SolutionIs their any relationship between wave speed and the maximum partcle speed for a wave travelling on a string? If so, what is it?
View SolutionCalculate the velocity of a transverse wave along a string of length `2 m` and mass `0.06 kg` under a tension of `500 N`.
View SolutionCalculate the speed of a transverse wave in a wire of `1.0 mm^(2)` cross-section under a tension of `0.98 N`. Density of the material of wire is `9.8 xx 10^(3) kg//m^(3)`
View SolutionIf at `t = 0`, a travelling wave pulse in a string is described by the function,
`y = (10)/((x^(2) + 2 ))`
Hence, `x and y` are in meter and `t` in second. What will be the wave function representing the pulse at time `t`, if the pulse is propagating along positive x-axix with speed `2 m//s`?
View SolutionConsider a sinusoidal travelling wave shown in figure. The wave velocity is `+ 40 cm//s`.
Find
(a) the frequency
(b) the phase difference between points `2.5 cm` apart
(c) the velocity of a particle at `P` at the instant shown.
View SolutionThe equation of a travelling wave is
`y(x, t) = 0.02 sin ((x)/(0.05) + (t)/(0.01)) m`
Find (a) the wave velocity and
(b) the particle velocity at `x = 0.2 m and t = 0.3 s`.
View SolutionTransverse waves on a srting have speed `12.0 m//s`, amplitude `0.05 m` and wavelength `0.4 m`. The waves travel in the `+ x-direction` and at `t = 0` the `x = 0` end of the string has zero displacement and is moving upwards.
(a) Write a wave function describing the wave.
(b) Find the transverse displacement of a point at `x = 0.25 m` at time `t = 0.15 s`.
( c ) How much time must elapse from the instant in part (b) until the point at `x = 0.25 m` has zero dispacement?
View SolutionA wave is described by the equation `y = (1.0 mm) sin pi((x)/(2.0 cm) - (t)/(0.01 s))`.
(a) Find time period and wavelength.
(b) Find the speed of particle at `x = 1.0 cm` and time `t = 0.01 s`.
( c ) What are the speed of the partcle at `x = 3.0 cm`, `5.0 cm and 7.0 cm` at `t = 0.01 s`?
(d) What are the speeds of the partcle at `x =1.0 cm` at `t = 0.011` , `0.012 and 0.013 s`?
View SolutionA sinusoidal wave travelling in the positive x-direction has an amplitude of `15.0 cm`, a wavelength of `40.0 cm` and a frequency of `8.00 Hz. The verticle displacement of the medium at `t = 0 and x = 0` is also `15.0 cm` as shown in figure.

(a) Find the angular wave number `k`, period `T`, angular frequency `omega` and speed `v` of the wave.
(b) Write a general expression for wave function.
View SolutionA flexible steel cable of total length `L` and mass per unit length `mu` hangs vertically from a support at one end. (a) Show that the speed of a transverse wave down the cable is `v =sqrtg(L - x)`, where `x` is measured from the support. (b) How long will it takes for a wave to travel down the cable?
View SolutionA loop of rope is whirled at a high angular velocity`omega`, so that it becomes a taut circle of radius`R`. A kink develops in the whirling rope.
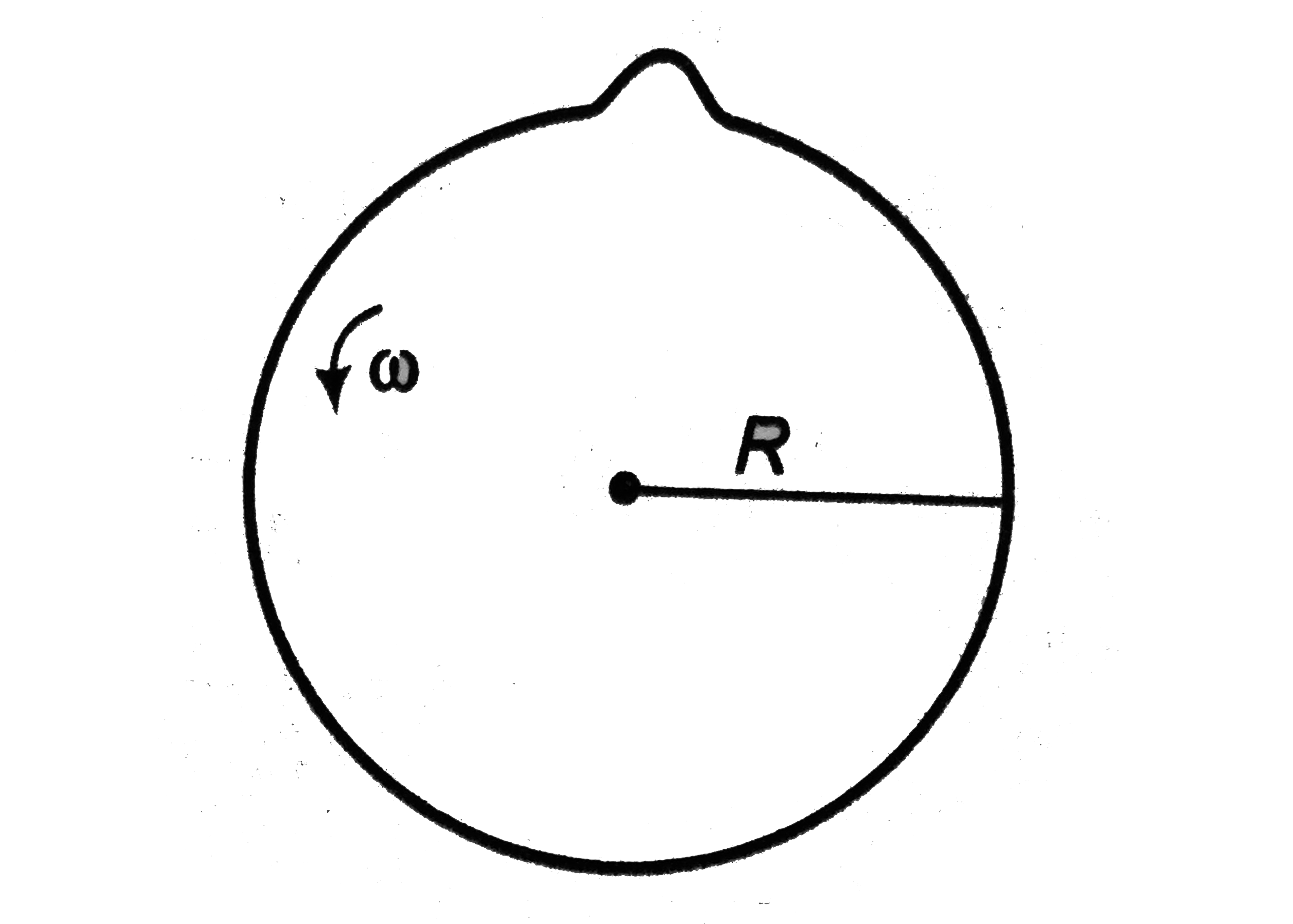
(a) Show that the speed of the kink in the rope is `v = omegaR`.
(b) Under what conditions does the kink remains stationary relative to an observer on the ground?
View SolutionA non-uniform wire of length `l` and mass `M` has a variable linear mass density given by `mu = kx`, where `x` is distance from one end of wire and `k` is a constant. Find the time taken by a pulse starting at one end to reach the other end when the tension in the wire is `T`.
View SolutionThe speed of propagation of a wave in a medium is `300m//s`. The equation of motion of point at `x = 0` is given by `y = 0.04 sin 600 pit(metre)`. The displacement of a point `x=75cm` at `t=0.01 s` is
View Solution
Level 1 Subjective questions and complete solutions for chapter WAVE MOTION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS WAVE MOTION
- Comprehion Type Questions
- Example
- Example Type 1
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Exercise 17.1
- Exercise 17.2
- Exercise 17.3
- Exercise 17.4
- Exercise 17.5
- Exercise 17.6
- Integer Type Question
- JEE MAINS
- Level 1 Assertion And Reason
- Level 1 Objective
- Level 1 Subjective
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Matrix Matching
- Miscellaneous Examples
- More Than One Option is Correct
- Objective Questions
- ONLY ONE OPTION IS CORRECT
- Subjective Questions
- Type 5