Complete Solutions to Example of chapter SUPERPOSITION OF WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SUPERPOSITION OF WAVES |
| DC PANDEY | Example |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
In interference, two individual amplitudes are `A_0` each and the
intensity is `I_0` each. Find resultant amplitude and intensity at a point, where:
(a) phase difference between two waves is `60^@`.
(b) path difference between two waves is `lambda/3`.
View SolutionThree waves from three coherent sources meet at some point. Resultant amplitude of each is `A_0`. Intensity corresponding to `A_0 is I_0`. Phase difference between first wave and second wave is `60^@`. Path difference between first wave and third wave is `lambda/3`. The first wave lags behind in phase angle from second and third wave. Find resultant intensity at this point.
View SolutionTwo waves of equal frequencies have their amplitude in the ratio of 5:3. They are superimposed on each other. Calculate the ratio of the maximum to minimum intensities of the resultant wave.
View SolutionIn interference, `I_(max)/I_(min) = alpha` , find
(a) ` A_(max)/A_(min)` (b)` A_1/A_2` (c)`I_1/I_2` .
View SolutionThe displacement of a standing wave on a string is given by
`y (x,t) = 0.4 sin (0.5x) cos (30t)`
where x and y are in centimetres.
(a) Find the frequency, amplitude and wave speed of the component waves.
(b) What is the particle velocity at `x=2.4 cm` at `t=0.8 s`?
View SolutionThe vibrations of a string of length 60 cm fixed at both ends are represented by the equation `y=4sin((pix)/15) cos (96 pi t)`, where x and y are in cm and t in seconds.
(a)What is the maximum displacement of a point at `x = 5cm`?
(b)Where are the nodes located along the string?
(c)What is the velocity of the particle at x=7.5cm and t=0.25s?
(d)Write down the equations of the component waves whose superposition gives the above wave.
View SolutionIn terms of T, `mu` and l, find frequency of
(a) fourth overtone mode
(b) third harmonic .
View SolutionA massless rod of length `L` is suspened by two identical string `AB` and `CD` of equal length. A block of mass `m` is suspended from point `O` such that `BO` is equal to 'x'. Further it is observed that the frequency of `1st` harmonic in `AB` is equal to `2nd` harmonic frequency in `CD`. 'x' is
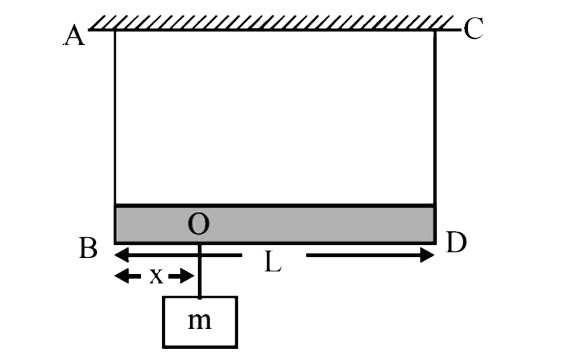
View SolutionAn object of specific gravity `rho` is hung from a thin steel wire. The fundamental frequency for transverse standing waves in wire is `300 Hz`. The object is immersed in water so that one half of its volume is submerged. The new fundamental frequency in `Hz` is
View SolutionTwo strings 1 and 2 are taut between two fixed supports (as shown in figure) such that the tension in both strings is same. Mass per unit length of 2 is more than that of 1. Explain which string is denser for a transverse travelling wave.
 .
.
View SolutionA sound wave and a light wave are reflected and refracted (or transmitted) from water surface. Show the changes in different physical quantities associated with a wave.
View SolutionA harmonic wave is travelling on string 1. At a junction with string 2 it is partly reflected and partly transmitted. The linear mass density of the second string is four times that of the first string, and that the boundary between the two strings is at x=0. If the expression for the incident wave is
`y_i = A_i cos (k_1 x-omega_1t)`
(a) What are the expressions for the transmitted and the reflected waves in terms of `A_i, k_1` and `omega_1`?
(b) Show that the average power carried by the incident wave is equal to the sum of the average power carried by the transmitted and reflected waves.
View SolutionFrom energy conservation principle prove the relations,
`A_r = ((v_2-v_1)/(v_1 +v_2))A_i` and `A_t = ((2v_2)/(v_1 +v_2))A_i`
Here, symbols have their usual meanings.
View Solution
Example questions and complete solutions for chapter SUPERPOSITION OF WAVES of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS SUPERPOSITION OF WAVES
- Example
- Example Type 1
- Example Type 2
- Example Type 3
- Example Type 4
- Exercise 18.1
- Exercise 18.2
- Exercise 18.3
- Exercise 18.4
- Level 1 Assertion And Reason
- Level 1 Objective
- Level 1 Subjective
- Level 2 Comprehension Based
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Example
- More than One correct Options
- Objective Questions
- Subjective Questions