Complete Solutions to Level 1 Subjective of chapter SUPERPOSITION OF WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SUPERPOSITION OF WAVES |
| DC PANDEY | Level 1 Subjective |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
Two waves are travelling in same direction along a stretched string. The waves are `90^@` out of phase. Each wave has an amplitude of 4.0 cm. Find the amplitude of the resultant wave.
View SolutionTwo wires of different densities are soldered together end to end then stretched under tension T. The waves speed in the first wire is twice that in the second wire.
(a) If the amplitude of incident wave is A, what are amplitudes of reflected and transmitted waves?
(b) Assuming no energy loss in the wire, find the fraction of the incident power that is reflected at the junction and fraction of the same that is transmitted.
View SolutionA wave is represented by
`y_1 = 10 cos (5x + 25 t)`
where, x is measured in meters and t in seconds. A second wave for which
`y_2 = 20 cos (5x + 25t + pi/3)`
interferes with the first wave. Deduce the amplitude and phase of the resultant wave.
View SolutionTwo waves passing through a region are represented by `y=(1.0cm) sin [(3.14 cm^(-1))x - (157s^(-1) x - (157s^(-1))t]`
and `y = (1.5 cm) sin [(1.57 cm^(-1))x- (314 s^(-1))t].` Find the displacement of the particle at x = 4.5 cm at time t = 5.0 ms.
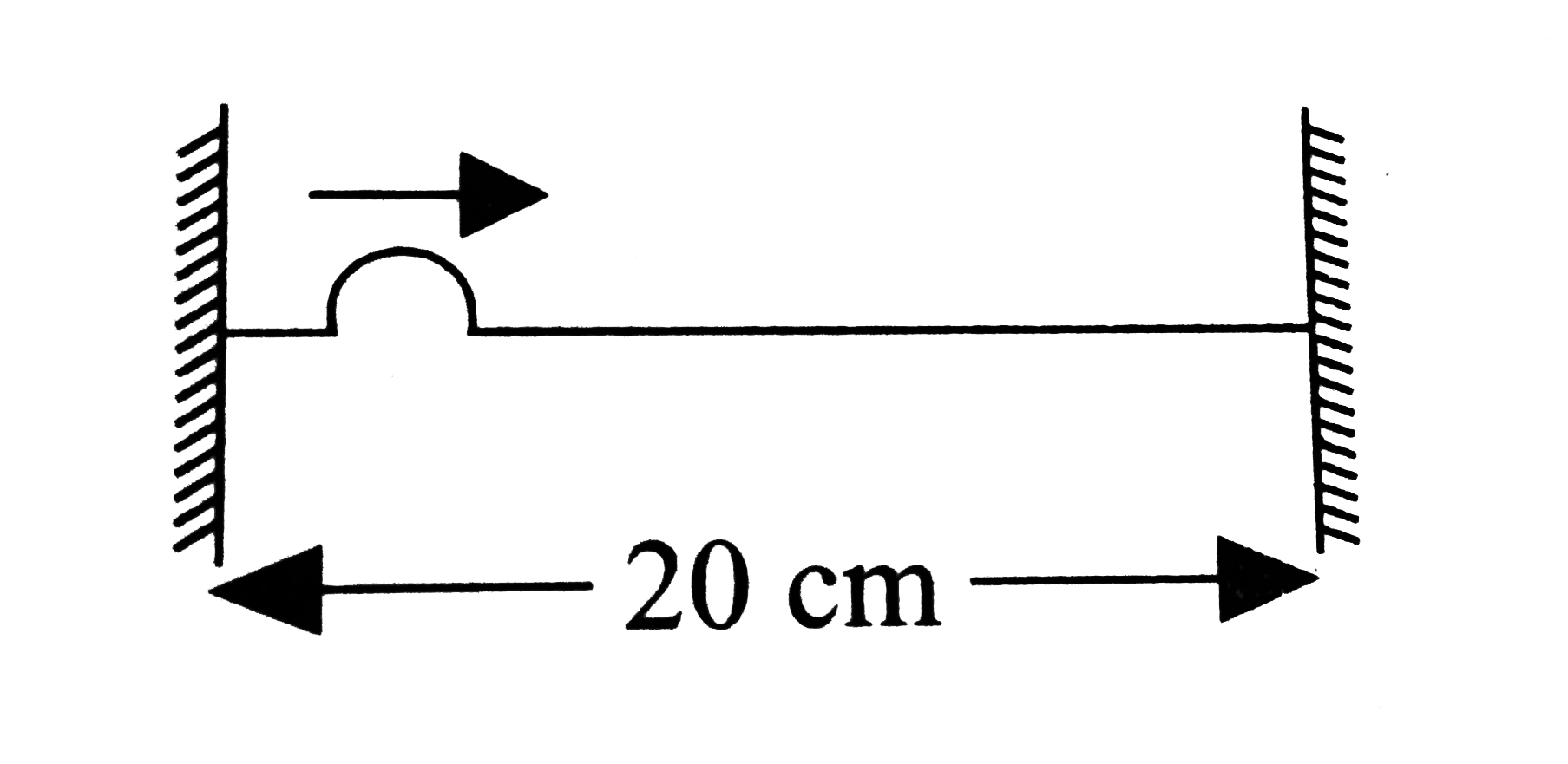
View SolutionA string of length `20 cm` and linear mass density `0.40 g//cm` is fixed at both ends and is kept under a tension of `16 N.A` wave pulse is produced at `t=0` nearj an end as shown in figure which travels towards the other end.
when will the string have the shape shown in the figure again? `(inxx10^(-2)s)`
View SolutionA wave pulse on a string has the dimensions shown in figure. The wave speed is `v=1 cm//s`.
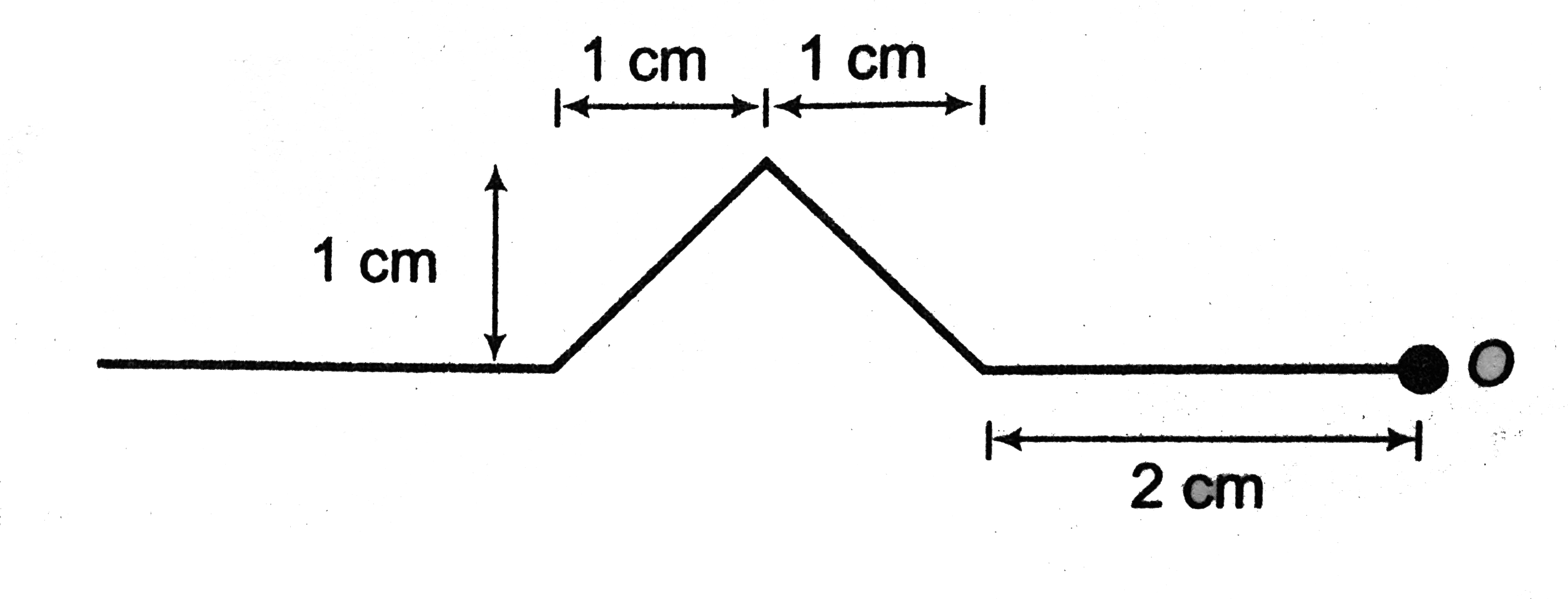
(a) If point O is a fixed end, draw the resultant wave on the string at t=3 s and t=4 s.
(b) Repeat part (a) for the case in which O is a free end.
View SolutionTwo sinusoidal waves combining in a medium are described by the equations
`y_1 = (3.0 cm) sin pi (x+ 0.60t)`
and `y_2 = (3.0 cm) sin pi (x-0.06 t)`
where, x is in centimetres and t is in seconds. Determine the maximum displacement of the medium at
(a)x=0.250 cm,
(b)x=0.500 cm and
(c) x=1.50 cm.
(d) Find the three smallest values of x corresponding to antinodes.
View SolutionA standing wave is formed by the interference of two travelling waves, each of which has an amplitude `A = pi cm` , angular wave number `k= (pi//2)` per centimetre.
(a) Calculate the distance between two successive antinodes.
(b) What is the amplitude of the standing wave at `x=0.50 cm` from a node?
View SolutionFind the fundamental frequency and the next three frequencies that could cause a standing wave pattern on a string that is 30.0 m long, has a mass per unit length of `9.00 xx 10^(-3) kg//m` and is stretched to a tension of 20.0 N.
View SolutionA string vibrates in its first normal mode with a frequency of `220` vibrations `//s`. The vibrating segment is 70.0 cm long and has a mass of 1.20g.
(a) Find the tension in the string.
(b) Determine the frequency of vibration when the string vibrates in three segments.
View SolutionA 60.0 cm guitar string under a tension of 50.0 N has a mass per unit length of 0.100 `g//cm.` What is the highest resonance frequency of the string that can be heard by a person able to hear frequencies upto 20000 Hz?
View SolutionA wire having a linear density of `0.05 g//cm`is stretched between two rigid supports with a tension of 450N. It is observed that the wire resonates at a frequency of 420 Hz. The next higher frequency at which the same wire resonates is 490 Hz. Find the length of the wire.
View SolutionThe vibrations from an 800 Hz tuning fork set up standing waves in a string clamped at both ends. The wave speed in the string is known to be `400 m//s ` for the tension used. The standing wave is observed to have four antinodes. How long is the string?
View SolutionA string vibrates in 4 segments to a frequency of 400 Hz.
(a) What is its fundamental frequency?
(b) What frequency will cause it to vibrate into 7 segments?
View SolutionA sonometer wire has a total length of 1m between the fixed ends. Where should the two bridges be placed below the wire so that the three segments of the wire have their fundamental frequencies in the ratio 1 : 2 : 3 ?
View SolutionA guitar string is 90 cm long and has a fundamental frequency of 124 Hz. Where should it be pressed to produce a fundamatal frequecy of 186 Hz?
View SolutionAdjacent antinodes of a standing wave on a string are 15.0 cm apart. A particle at an antinode oscillates in simple harmonic motion with amplitude 0.850 cm and period 0.0750 s. The string lies along the +x-axis and is fixed at x=0.
(a) find the displacement of a point on the string as a function of position and time.
(b) Find the speed of propagation of a transverse wave in the string.
(c) Find the amplitude at a point 3.0 cm to the right of an antinode.
View SolutionA 1.50 m long rope is stretched between two supports with a tension that makes the speed of transverse waves 48.0`m//s`. What are the wavelength and frequency of
(a) the fundamental?
(b) the second overtone?
(c) the fourth harmonic?
View SolutionA wire with mass 40.0 g is stretched so that its ends are tied down at points 80.0 cm apart.The wire vibrates in its fundamental mode with frequency 60.0 Hz and with an amplitude at the antinodes of 0.300 cm.
(a) What is the speed of propagation of transverse wave in the wire?
Compute the tension in the wire.
(c) Find the maximum transverse velocity and acceleration of particles in the wire.
View SolutionTwo harmonic waves are represented in SI units by
`y_1(x,t) = 0.2 sin (x-3.0t) and y_2(x,t) = 0.2 sin (x- 3.0t + phi)`
(a) Write the expression for the sum `y=y_1 + y_2 for phi = pi/2 rad.`
(b) Suppose the phase difference `phi` between the waves is unknown and the amplitude of their sum is 0.32 m, what is `phi`?
View SolutionFigure shows different standing wave patterns on a string of linear mass density `4.0 xx 10^-2 kg//m` under a tension of 100 N. The amplitude of antinodes is indicated in each figure. The length of the string is 2.0m.
(i) Obtain the frequencies of the modes shown in figures (a) and (b).
(ii)Write down the transverse displacement y as a function of x and t for each mode. (Take the initial configuration of the wire in each mode to be as shown by the dark lines in the figure).

View SolutionA string fastened at both ends has successive resonances with wavelengths of 0.54 m for nth harmonic and 0.48 m for the (n+1) th harmonic and 0.48 m for the (n+1) th harmonic.
(a) Which harmonics are these?
(b) What is the length of the stirng?
(c) What is the wavelength of the fundamental frequency?
View SolutionA wave `y_i = 0.3 cos (2.0x - 40t)` is travelling along a string toward a boundary at x=0. Write expressions for the reflected waves if .
(a) the string has a fixed end at x=0 and
(b) The string has a free end at x=0.
Assume SI units.
View SolutionA string that is 10 cm long is fixed at both ends. At t=0, a pulse travelling from left to right at `1cm//s is 4.0 cm ` from the right end as shown in figure. Determine the next two times when the pulse will be at that point again. State in each case whether the pulse is upright or inverted .
 .
.
View Solution
Level 1 Subjective questions and complete solutions for chapter SUPERPOSITION OF WAVES of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS SUPERPOSITION OF WAVES
- Example
- Example Type 1
- Example Type 2
- Example Type 3
- Example Type 4
- Exercise 18.1
- Exercise 18.2
- Exercise 18.3
- Exercise 18.4
- Level 1 Assertion And Reason
- Level 1 Objective
- Level 1 Subjective
- Level 2 Comprehension Based
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Example
- More than One correct Options
- Objective Questions
- Subjective Questions