Complete Solutions to Level 1 Subjective of chapter SOUND WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SOUND WAVES |
| DC PANDEY | Level 1 Subjective |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
Dentermine the speed of sound waves in water , and find the wavelength of a wave having a frequency of `242 H_(Z)` . Take `B_(water) = 2xx10^(9) Pa`.
View SolutionIf the source and reciver are at rest realative to each other but the wave medium is moving realative to them, will the reciver delect wavelength or frequency shift.
View SolutionUsing the fact that hydrogen gas consister of diatomic molecules with `M = 2 kg//K - mol`. Find the speed of sound in hydrogen at `27^(@) C` .
View SolutionAbout how many times more intense will the normal ear perceiver a sound of `10 ^(6) W //m^(2)` than one of `10^(9) W//m^(2)` ?
View SolutionA `300 H_(Z)` source, an observer and a wind are moving as shows in the figure with respect to the ground. What frequency is heard by observer ? Take speed of sound in air = `340 m//s` .
`underset(20m//s)overset(observer)(larr)` `underset(rarr)(rarr)5 m//s` `underset(10m//s)overset(source)(rarr)`
View SolutionA person standing between two parallel hills fires a gun. He hears the first echo after `(3) /(2)` s, and a second echo after `(5) /(2)` s. If speed of sound is `332 m//s` , Calculate the distance between the hills. When will he hear the third echo?
View SolutionHelium is a monatomic gas that has a density of `0.179 kg//m^(3)` at a pressure of `76 cm` of mercury and a temperature of `0^(@) C` . Find the speed of compressional waves (sound) in helium at this temperature and pressure.
View Solution(a) In a liquid with density `1300 kg //m^(3)` , longitudinal waves frequency `400 H_(Z)` are found to have wavelength `8.00 m` . Calculate the bulk modulus of the liquid. (b) A metal bar with a length of `1.50 m` has density `6400 kg//m^(3)` . Longitudinal sound waves take `3.90xx10^(-4)` s to travel from one end of the bar to the other. What is young's modulus for this metal?
View SolutionWhat must be the stress `(F//A)` in a stretched wire of a material whose Young's modulus is `Y` for the speed of lonitudinal waves equal to `30` times the speed of transverese waves?
View SolutionA gas is a mixture of two parts by volume of hyprogen and part by volume of nitrogen at `STP`. If the velocity of sound in hydrogen at `0^(@) C` is `1300 m//s` . Find the velocity of sound in the gaseous mixure at `27^(@)C`.
View SolutionThe explosion of a fire cracker in the air at the a heigth of `40 m` produced a `100 dB` sound level at ground below. What is the instantaneous total radiated power? Assuming that it radiates as a point source.
View Solution(a) What is the intensity of a `60 dB` sound ? (b) If the sound level is `60 dB` close to a speaker that has an area of `120 cm ^(2)` . What is the acoustic power output of the speaker?
View Solution(a) By what factor must the sound intensity be increased the sound intensity level by `13.0 dB` ? (b) Explain why you do not need to know the original sound intersity ?
View SolutionThe speed of a certain compressional wave in air at standard temperature and pressure is `330 m//s` . A point source of frequency `300 H_(Z)` radiates energy uniformly in all directions at the rate of `5` Watt. (a) What is the intensity of the wave at a distance of `20 m` from the source? (b) What is the amplitude of the wave there? [ Density of air at `STP = 1.29 kg //m^(3)`]
View SolutionWhat is the amplitude of motion for the air in the path of a `60 dB` , `800 H_(Z)` sound wave? Assume that `rho_(air)= 1.29 kg//m^(3)` and `upsilon = 330 m//s`.
View SolutionA rock band give rise to an average sound level of `102 dB` at a distance of `20 m` from the center of the band . As an approximation , assume that the band radiates sound equally into a sphere. What is the sound power output of the band?
View SolutionIf it were possible to generate a sinusoidal `300 H_(Z)` sound wave in air that has a displacement amplitude of `0.200 mm` . What would be the sound level ? (Assume `upsilon = 330 m//s` and `rho_(air) = 1.29 kg//m^(3))`
View Solution(a) A longitudinal wave propagating in a water-filled pipe has intensity `3.00xx10^(-6) W//m ^(2)` and frequency `3400 H_(Z)` . Find the amplitude `A` and wavelength `lambda` of the wave . Water has density `1000 kg//m ^(3)` and bulk modulus `2.18xx10^(9) Pa`. (b) If the pipe is filled with air at pressure `1.00 xx10^(5)` Pa and density `1.20 kg//m^(3)`, What will be the amplitude `A` and wavelength `lambda` of a longitudinal wave the same intensity and frequency as in part (a) ? (c ) In which fluid is the amplitude larger, water or air? What is the ratio of the two amplitude ? Why is this ratio so different from/ Conider air as diatomic.
View SolutionFor a person with normal hearing, the faintest sound that can be heard at a frequency of `400 Hz` has a pressure amplitude of about `6.0 xx 10^(-5)` Pa . Calculate the corresponding intensity and sound intensity lavel at `20^(@) C`. (Assume `upsilon = 330 m//s` and `rho _(air) = 1.29 kg //m^(3)`).
View Solutionfind the fundamental frequency and the frequency of the first two overtones of a pipe `45.0 cm` long. (a) If the pipe is open at both ends. (b) If the pipe is closed at one end. Use `upsilon = 344 m//s` .
View SolutionWrite the equation for the fundamental standing sound waves in a tube that is open at both ends. If the tube is `80 cm` long speed of wave is `330 m//s` . Represent the amplitude of the wave at an antinode by `A` .
View SolutionA long glass tube is held vertically , dipping into water, while a tuning fork of frequency `512 H_(Z)` is respeatedly struck and held over the open end. Strong resonance is obtained, when the length of the tube above the surface of water is `50 cm` and again `84 cm`, but not at any intermediate point. Find the speed of sound of sound in air and next length of the air column for resonance.
View SolutionA wire of length `40 cm` which has a mass of `4` g oscillates in its second harmonic and sets the air column in the tube to vibrations in its funrations in its fundamental mode as shows in figure. Assuming the speed of sound in air as `340 m//s` . Find the tension in the wire.

View SolutionIn a resonance tube experiment to determine the speed of sound in air, a pipe of diameter `5 cm` is used . The column in pipe resonates with a tuning fork of frequency `480 H_(Z)` when the minimum length of the air column is `16 cm` . Find the speed in air column at room temperature.
View SolutionOn a day when the speed is `345 m//s`, the fundamental frequency of a closed organ pipe is `220 H_(Z)` . (a) How long is this closed pipe? (b) The second overtone of this pipe has the same wavelength as the third harmonic of an open pipe . How long is the open pipe ?
View SolutionA closed organ pipe is sounded near a guitar, causing one of the string to vibrate with large amplitude . We vary the tension of the string until we find the maximum amplitude. The string is `80%` as long as the closed pipe. If both the pipe and the string vibrate at their fundamental frequency, calculate the ratio of the wave speed on the string to the speed of sound in air.
View SolutionA police siren emits a sinusoidal wave with frequency `f_(S) = 300 H_(z)` . The speed of the sound is `340 m//s`. (a) Find the wavelength of the waves if siren is at rest in the air . (b) If the siren is moving at `30 m//s`, Find the wavelength of the waves ahead of and behind the source.
View SolutionTwo identical violin strings, when in true and stretched with same tension , have a fundamental frequency of `440.0 H_(Z)`. One of the string is retuned by adjusting its tension . When this is done, `1.5` beats per second are heard when both strings are plucked simultaneously. (a) What are the possible fundamental frequencies of the retuned string? (b) by what fractional amount was the string tension changed if it was (i) increased (ii) decreased?
View SolutionA swimming duck paddles the water with its feet once every `1.6` s, producing surface waves with this period. The duck is moving at constant speed in a pond where the speed of surface waves is `0.32 m//s` , and the crests of the waves ahead of the duck are spaced `0.12 m` apart. (a) What is the duck's speed? (b) How far apart are the crests behind the duck?
View SolutionA railroad train is travelling at `30.0 m//s` in still air. The frequency of the note emitted by the train whistle is `262 H_(Z)` . What frequency is heard by a passenger on a train moving in the opposite direction to the first at `18.0 m//s` and (a) approaching the first? (b) receding from the first? Speed of sound in air = `340 m//s` .
View SolutionA boy is walking away from a well at a speed of `1.0 m//s` in a direction at right angles to the wall. As he walks, he below a whistle steadily. An observer towards whom the boy is walking hears `4.0` beats per second. If the speed of sound is `340 m//s` , what is the frequency of the whistle?
View SolutionA tuning fork `P` of unknows frequency gives `7` beats in `2` seconds with another tuning fork `Q`. When `Q` runs towards a wall with a speed of `5 m//s` it gives `5` beats per second with its echo. On loading `P` with wax, it gives `5` beats per second with `Q` . What is the frequency of `P`? Assume speed of sound = `332 m//s` .
View SolutionA stationary observer receives sonic oscillations from two tuning forks one of which approaches and the other recedes with the same velocity. As this takes place, the observer hears the beats of frequency `f = 2.0 H_(Z)`. Find the velocity of each tuning fork if their oscillation frequency is `f_(o) = 680 H_(Z)` and the velocity of sound in air is `upsilon = 340 m//s`.
View SolutionSound waves from a tuning fork `A` reacha point `P` by two separate paths `ABP` and `ACP`. When `ACP` is greater than `ABP` by `11.5 cm`, there is silence at `p`. When the difference is `23 cm` the sound becomes loudest at `P` and `34.5 cm` there is silence again and so on. Calculate the minimum frequency of the fork if the velocity of sound is taken to be `331.2 m//s`.
View SolutionTwo loudspeakers `S_(1)` and `S_(2)` each emit sounds of frequency `220 H_(Z)` uniformly in all directions. `S_(1)` has an acoustic output of `1.2 xx 10^(-3) W` and `S_(2)` has `1.8 xx 10 ^(-3) W` . `S_(1)` and `S_(2)` vibrate in phase.Consider a point `P` such that `S_(1) P = 0.75 m` and `S_(2) p = 3 m` . How are the phases arriving at `P` related? What is the intensity at `P` when both `S_(1)` and `S_(2)` are on ? Speed of sound in air is `330 m//s`.
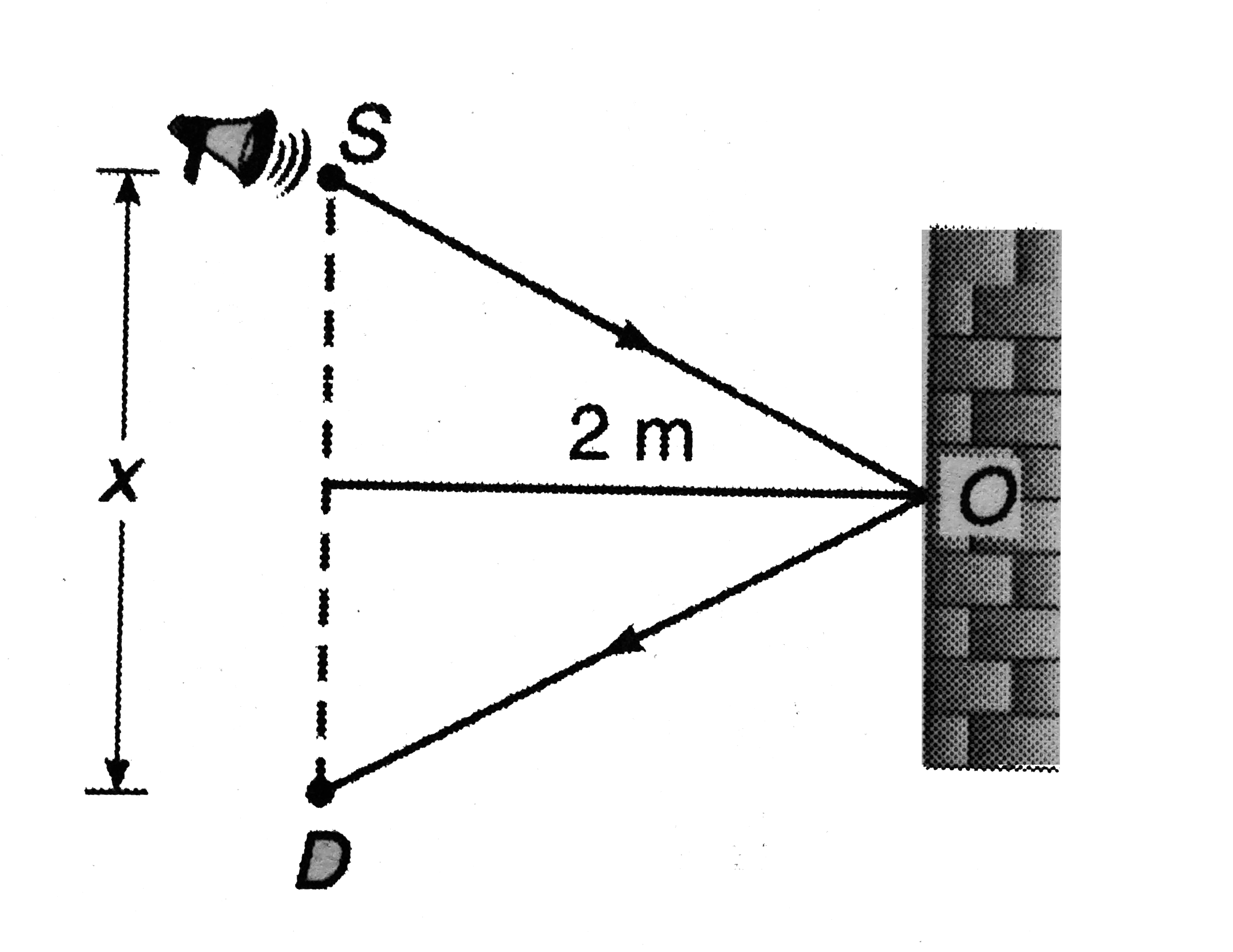
View SolutionA source of sound emitting waves at `360 H_(Z)` is placed in front of a vertical wall, at a distance `2 m` from it. A detector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and the detestor for which the detector detects a maximum of sound. Take speed of sound in air`= 360 m//s`. Assume that there is not phase change in reflected wave.
View SolutionThe atomic mass of iodine is `127 g//mol`. A standing wave in iodine vapour at `400 k` has nodes that are `6:77 cm` apart when the frequency is `1000 H_(Z)`. At this temperature, is iodine vapour monatomic or diatomic.
View SolutionA tuning fork whose natural frequency is `440 H_(Z)` is placed just above the open end of a tube that contains water. The water is slowly drained from the tube while the tuning fork remains in place and is kapt vibrating. The sound is found to be echanced when the air column is `60 cm` long and when it is `100 cm` long . Find the speed of sound in air.
View SolutionA piano wire `A` vibrates at a fundamental frequency of `600 H_(Z)`. A second identical wire `B` produces `6` beats per second with it when the tension in `A` is slightly increased. Find the ratio of the tension in `A` to the tension in `B`.
View SolutionA tuning fork of frequency `256 H_(Z)` produces `4` beats per second with a wire of legth `25 cm` vibrating in its fundamental mode. The beat frequency decrease when the length is slightly shortened. What could be the minimum length by which the wire be shortened so that it produces no beats with the tuning fork?
View SolutionShow that when the speed of the source and the observer are small compared to the speed of sound in the medium, the change in frequency becomes independent of the fact whether the source is moving or the observer.
View SolutionA sound source moves with a speed of `80 m//s` relative to still air toward a stationary listener. The frequency of sound is `200 H_(Z)` and speed of sound in air is `340 m//s`. (a) Find the wavelength of the sound between the source and the listener. (b) Find the frequency heard by the listener.
View SolutionA railroad train is travelling at `30 m//s` in still air. The frequency of the note emitted by the node emitted by the locomotive whistle is `500 H_(Z)`. What is the wavelength of the sound waves : (a) in front of the locomotive?
What is the frequency of the sound heard by a stationary listener (b) behind the locomotive? (c) in front of the locomotive ?
Speed of sound in air `344 m//s`. (d) behind the locomotive ?
View SolutionFor a certain organ pipe, three successive resonance frequencies are observer at `425`, `595` and `765 H_(Z)` respectively. Taking the speed of sound in air to be `340 m//s`, (a) explain whether the pipe is closed at one or open at boyh ends. (b) determine the fundamental frequency and length of the pipe.
View SolutionTwo tuning forks `A` and `B` sounded together give `8` beats per second. With an air resonance tube closed at one end, the two forks give resonances when the two air columns are `32 cm` and `33 cm` respectively. Calculate the frequenciec of forks.
View Solution
Level 1 Subjective questions and complete solutions for chapter SOUND WAVES of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS SOUND WAVES
- Comprehension Based Questions
- Example
- Example Type 1
- Example Type 2
- Example Type 3
- Example Type 4
- Exercise 19.1
- Exercise 19.2
- Exercise 19.3
- Exercise 19.4
- Exercise 19.5
- Exercise 19.6
- Exercise 19.7
- INTRODUCTORY EXERCISE
- Level 1 Assertion And Reason
- Level 1 Objective
- Level 1 Subjective
- Level 2 Comprehension Based
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Examples
- More than One Correct Options
- Single correct option
- Subjective Questions
- TYPE 2.
- TYPE 5.