Complete Solutions to JEE Main of chapter ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MOTION |
| DC PANDEY MASTER PROBLEM PACKAGE | JEE Main |
| Number Of Questions | 63 |
| Academic Year | 2023-24 |
A circular disc A of radius r is made from an iron plate of thickness t and another circular disc B of radius 4r is made from an iron plate of thickness `t//4`. The relation between the moments of inertia `I_(A)` and `I_(B)` is (about an axis passing through centre and perpendicular to the disc)
03:57View SolutionA force F=`2hati+3hatj-hatk` acts at a point (2,-3,1). Then magnitude of torque about point (0,0,2) will be
03:50View SolutionA rod of weight w is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is.. And on B is......
03:55View SolutionA uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is
 04:28View Solution
04:28View SolutionIn the above problem, if the rod is released from horizontal position, the angular velocity of the rod as it passes the vertical position is (l=length fo rod)
View SolutionThree rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is
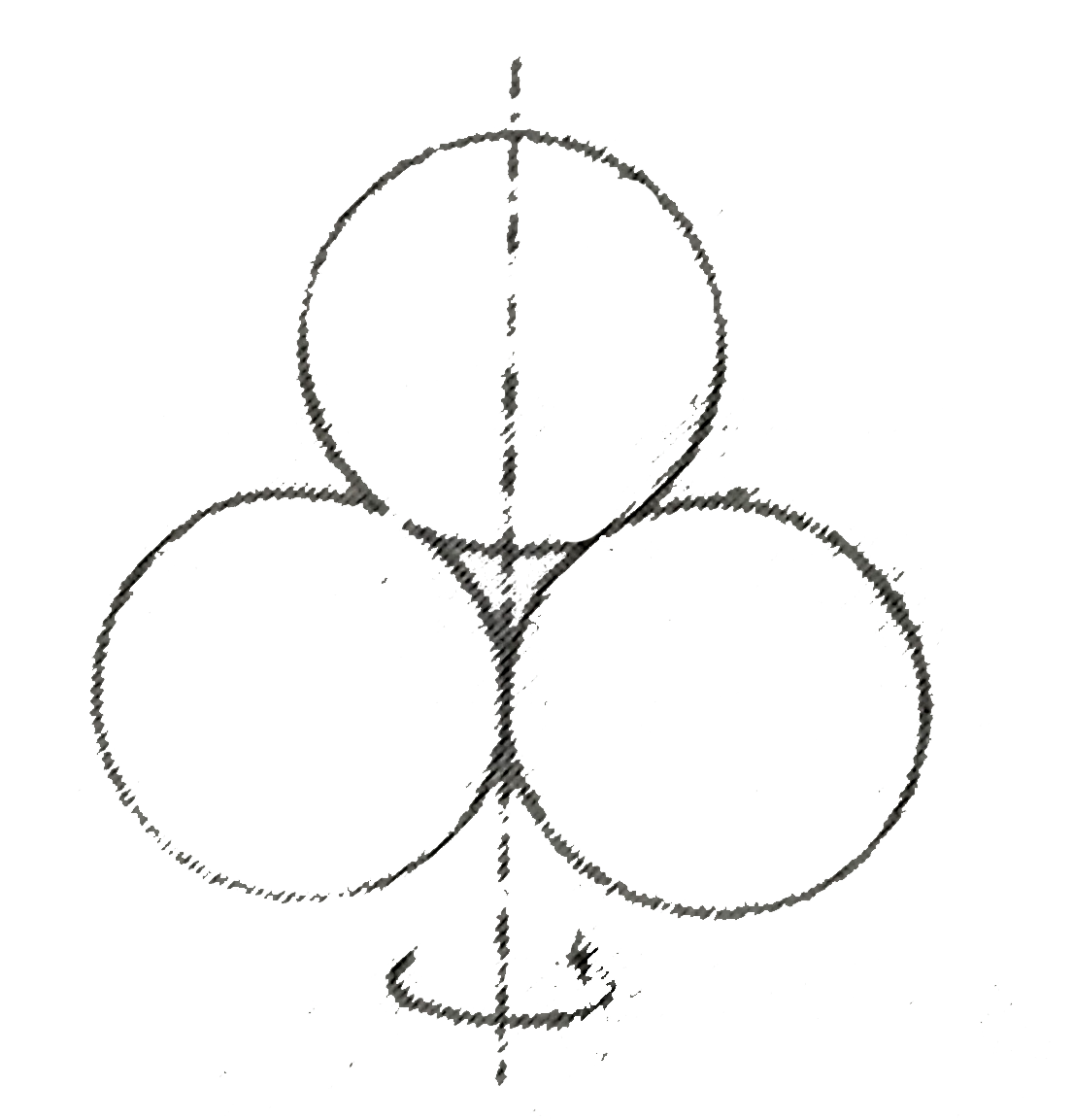 03:16View Solution
03:16View SolutionA plank `P` is placed on a solid cylinder `S`, which rolls on a horizontal surface. The two are of equal mass. There is no slipping at any of the surfaces in contact. The ratio of kinetic energy of `P` to the kinetic energy of `S` is:
 04:14View Solution
04:14View SolutionA disc is performing pure rolling on a smooth stationary surface with constant angular velocity as shown in Fig,. At any instant, for the lower most point of the disc,
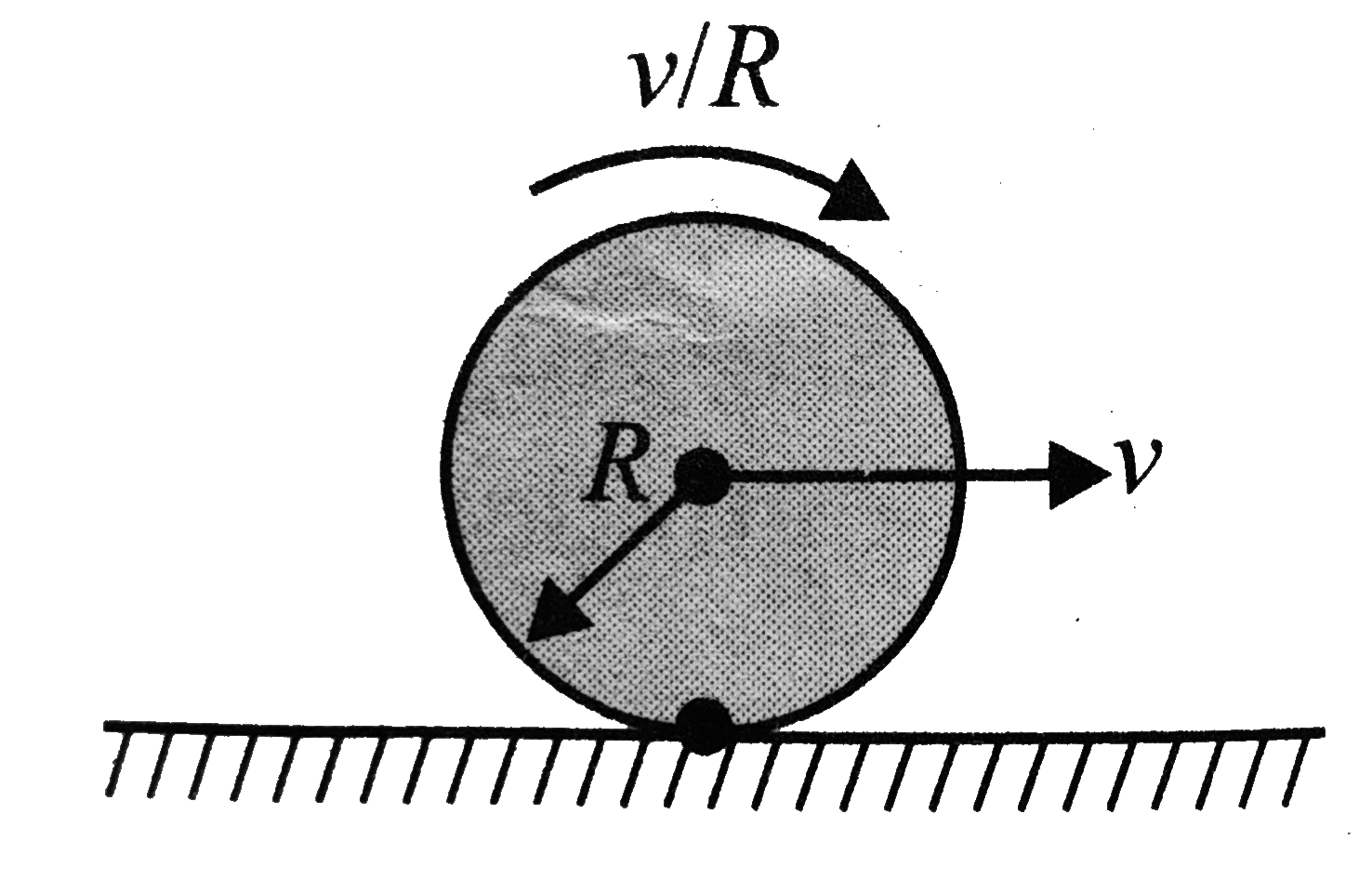 03:33View Solution
03:33View SolutionA ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is `k`. If radius of the ball be `R`, then the fraction of total energy associated with its rotation will be.
02:50View SolutionA particle of mass `2 kg` located at the position `(hati + hatj)m` has velocity `2(hati - hatj + hatk) m//s` . Its angular momentum about Z-axis in `kg m^(2)//s` is
02:52View SolutionA thin hoop of weight `500 N` and radius `1 m` rest on a rought inclined plane as shown in the figure. The minimum coefficient of friction needed for this configuration is.
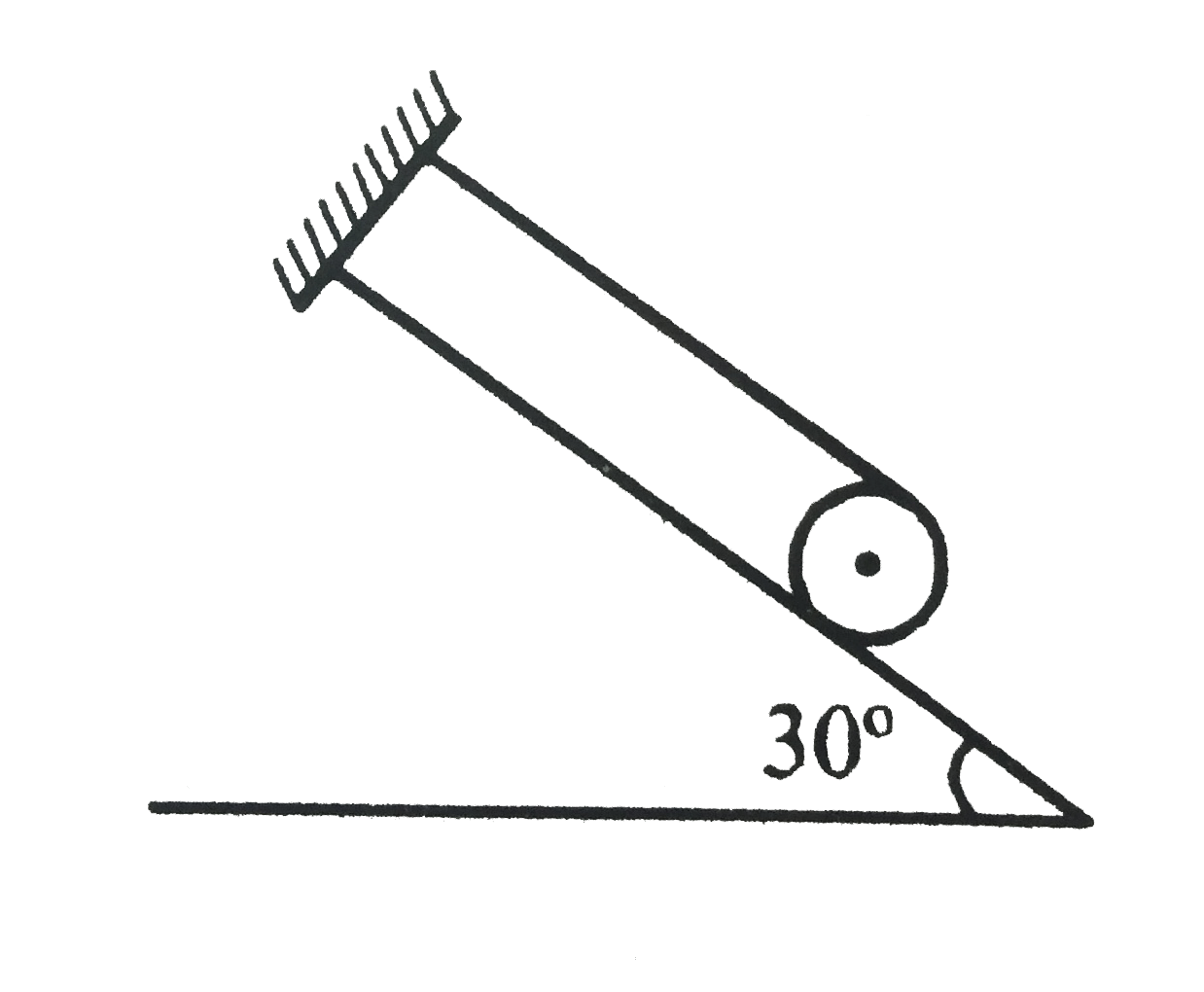 .02:32View Solution
.02:32View SolutionA pulley is hinged at the centre and a massless thread is wrapped around it. The thread is pulled with a contant froce `F` starting from rest. As the time increases -
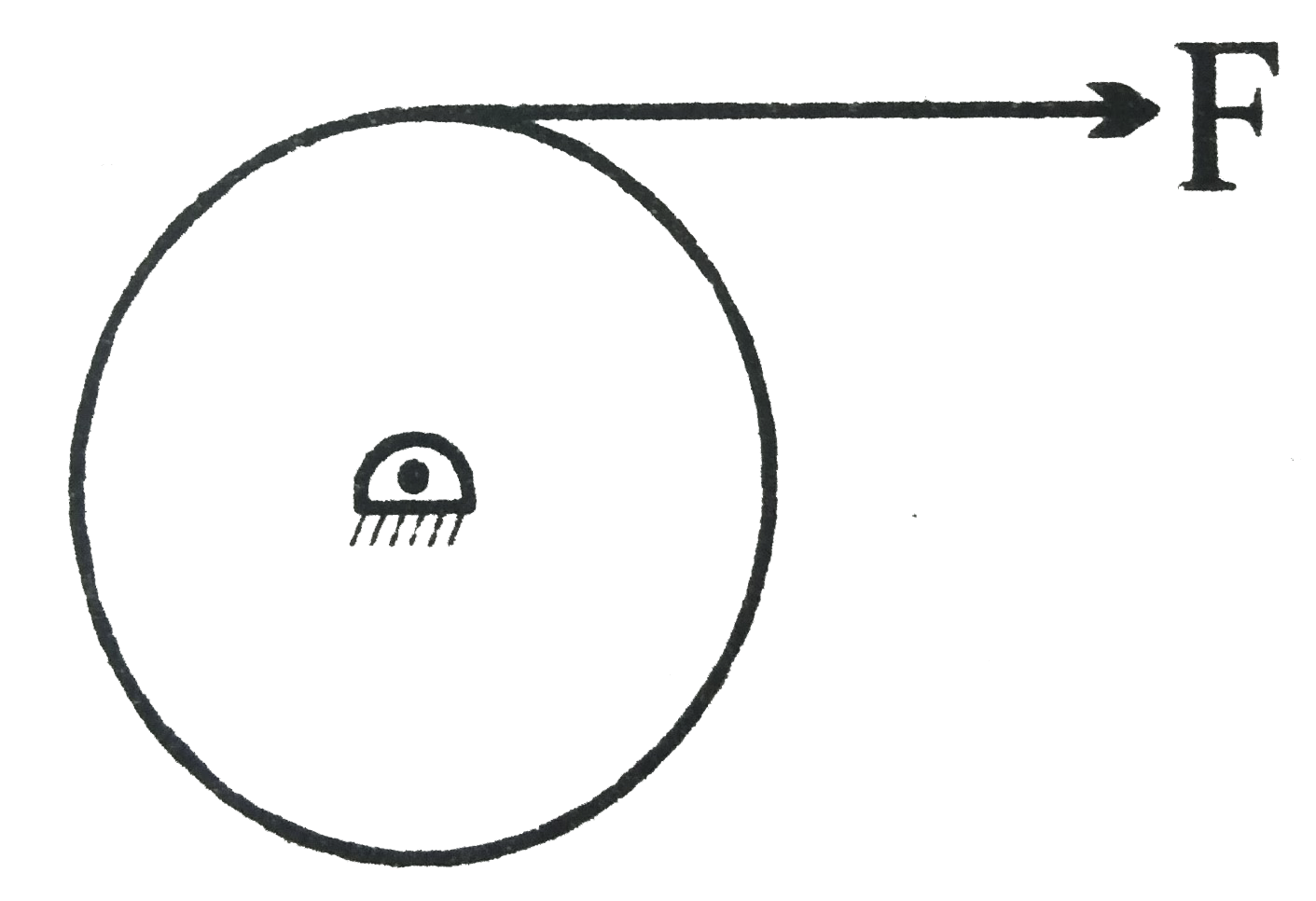 .01:58View Solution
.01:58View SolutionA solid uniform disc of mass `m` rolls without slipping down a fixed inclined plank with an acceleration a. The frictional force on the disc due to surface of the plane is
03:22View SolutionA weightless rod is acted upon by two upward parallel forces of `2 N` and `4 N` at ends `A` and `B` respectively. The total length of the rod `AB = 3 m`. To keep the rod in equilibrium a force of `6 N` should act in the following manner.
02:54View SolutionA rigid body can be hinged about any point on the x-axis. When it is hinged such that the hinge is at `x`, the moment of interia is given by
`I = 2 x^(2) - 12 x + 27`
The x-coordinate of centre of mass is.02:12View SolutionA particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
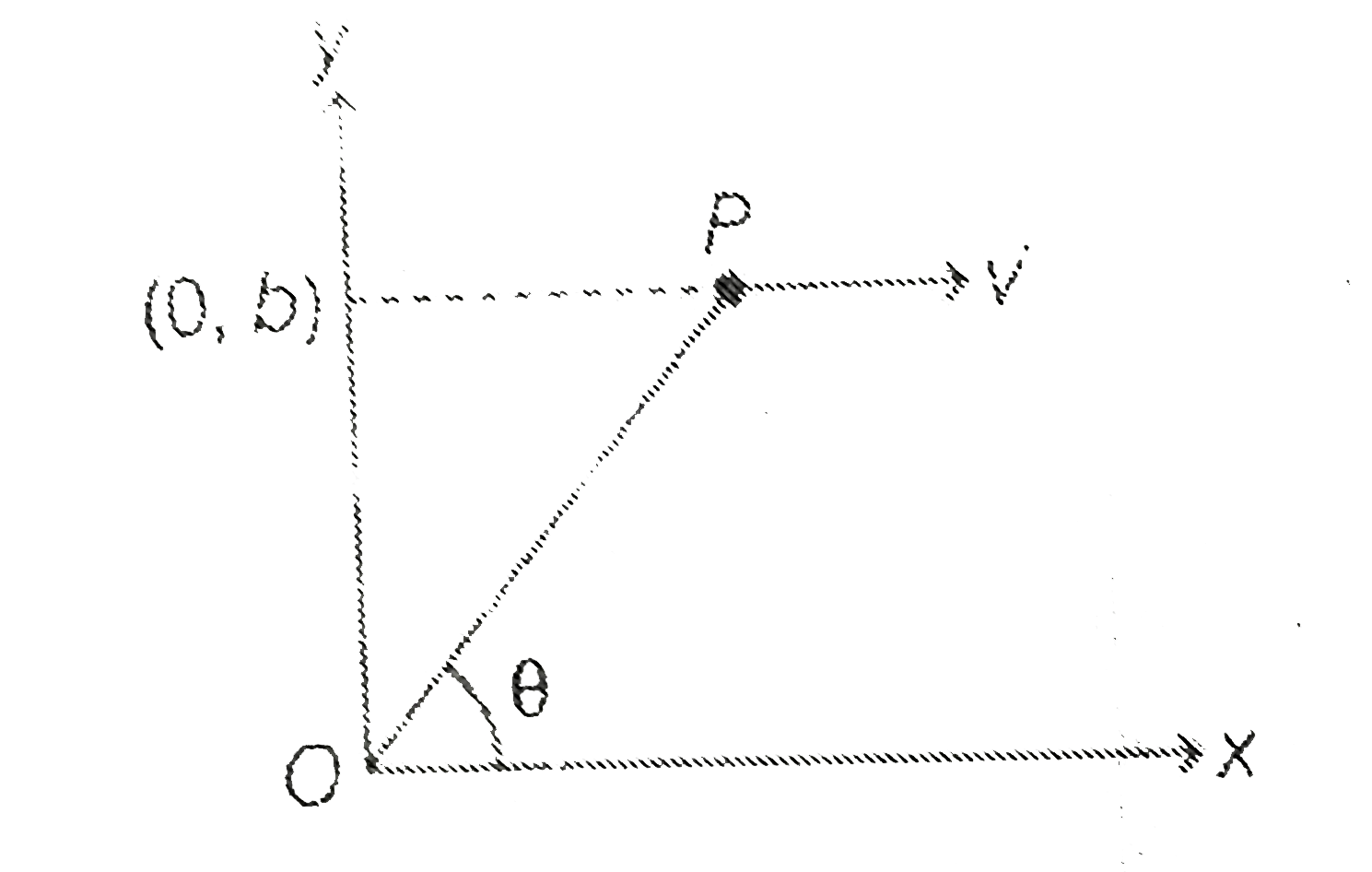 03:06View Solution
03:06View SolutionTwo men each of mass m stand on the rim of a horizontal circular disc, diametrically opposite to each other. The disc has a mass M and is free to rotate about a vertical axis passing through its centre of mass. Each mass start simultaneously along the rim clockwise and reaches their original starting positions on the disc. The angle turned through by disc with respect to the ground (in radian) is
03:16View SolutionWhen a solid sphere rolls without slipping down an inclined plane making an angle `theta` with the horizontal, the acceleration of its centre of mass is `a`. If the same sphere slides without friction, its.
03:24View SolutionTwo rings of same radius and mass are placed such that their centres are at a common point and their planes are perpendicular to each other. The moment of inertia of the system about an axis passing through the centre and perpendicular to the plane of one of the rings is (mass the ring `= m`, radius `= r`)
01:31View SolutionA uniform thin bar of mass `6 m` and length `12 L` is bend to make a regular hexagon. Its moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the hexagon is :
03:43View SolutionMoment of inertia `I` of a solid sphere about an axis parallel to a diameter and at a distance `x` from it varies as:
02:34View SolutionLocus of all the points in a plane on which the moment of inertia about all mutually parallel axes of a rigid body is same throughout is
01:41View SolutionThe moment of inertia of a uniform rod of length `2l` and mass `m` about an axis `xy` passing through its centre and inclined at an enable `alpha` is
 03:24View Solution
03:24View SolutionA wire of length `l` and mass `m` is bent in the form of a rectangle `ABCD` with `(AB)/(BC)=2`. The moment of inertia of this wife frame about the side `BC` is
05:22View SolutionA particle moves in a circle with constant angular velocity `omega` about a point P on its circumference. The angular velocity of the particle about the centre C of the circle is
02:09View SolutionTwo equal and opposite forces act on a rigid body at a certain distance. Then
02:22View SolutionA uniform stick of length l and mass m lies on a smooth table. It rotates with angular velocity `omega` about an axis perpendicular to the table and through one end of the stick. The angular momentum of the stick about the end is
01:48View SolutionA hoop rolls on a horizontal ground without slipping with linear speed `v`. Speed of a particle `P` on the circumference of the hoop at angle `theta` is :
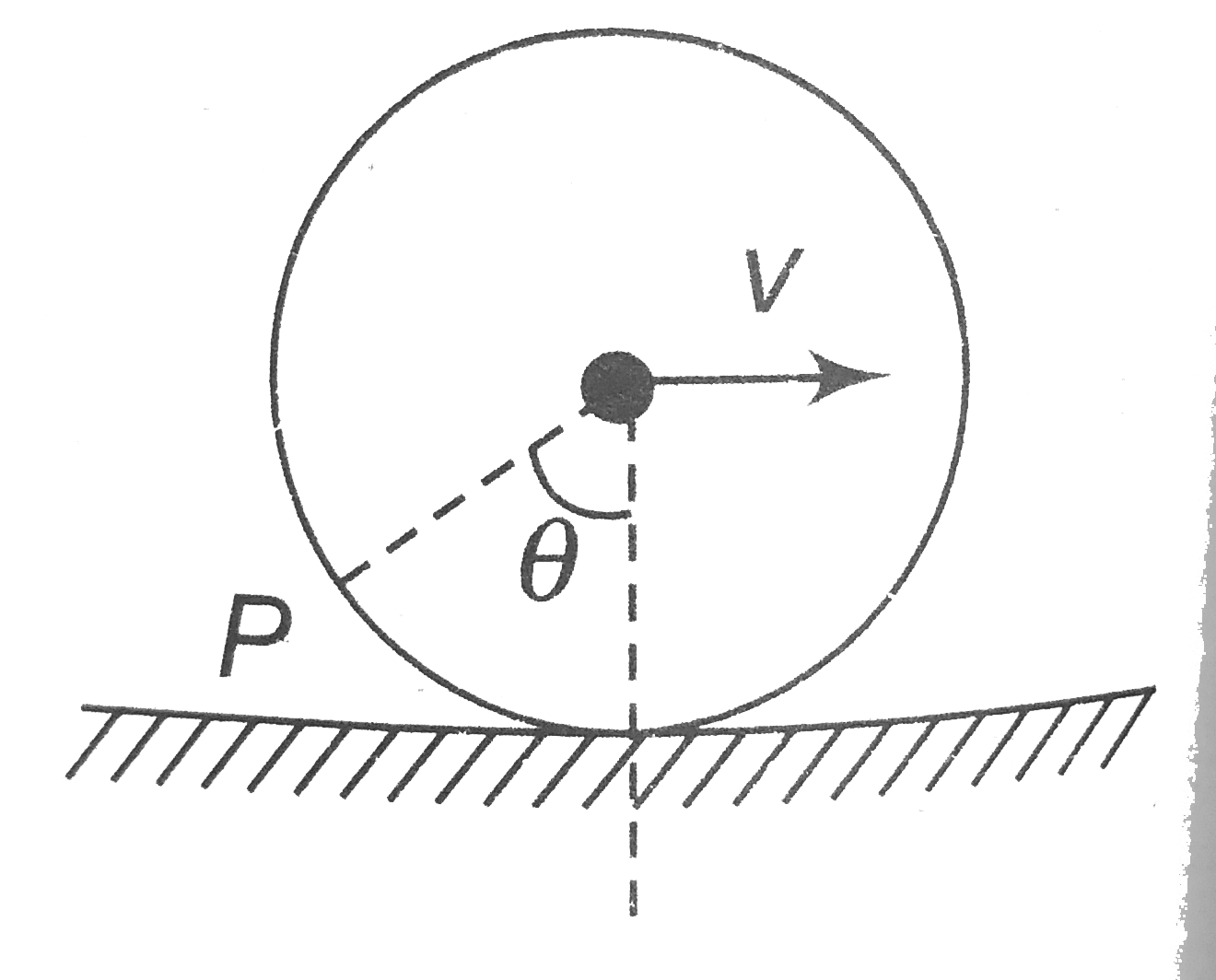 06:15View Solution
06:15View SolutionA disc is rotaing with an angular velocity `omega_(0)`. A constant retarding torque is applied on it to stop the disc. The angular velocity becomes `(omega_(0))/(2)` after n rotations. How many more rotations will it make before coming to rest ?
03:25View SolutionA uniform cube of side and mass m rests on a rough horizontal surface. A horizontal force F is applied normal to one face at point that is directly above the centre of the face at a height `(a)/(4)` above the centre. The minimum value of F for which the cube begins to topple above an edge without sliding is
03:01View SolutionA particle mass 1 kg is moving along a straight line `y=x+4`. Both x and y are in metres. Velocity of the particle is `2m//s`. Find the magnitude of angular momentum of the particle about origin.
03:14View SolutionA rigid spherical body is spinning around an axis without any external torque. Due to temperature its volume increases by `3%`. Then percentage change in its angular speed is:
04:40View SolutionA circular platform is mounted on a vertical frictionless axle. Its radius is `r = 2 m` and its moment of inertia`I = 200 kg m^2`. It is initially at rest. A `70 kg` man stands on the edge of the platform and begins to walk along the edge at speed `v_0 = 1 m s^-1` relative to the ground. The angular velocity of the platform is.
02:01View SolutionIn the above problem, when the man has walked once around the platform, so that he is at his original position on it, what is his angular displacement relative to ground?
View SolutionA solid sphere rolls down two different inclined planes of the same height but of different inclinations
07:46View SolutionAn inclined plane makes an angle of `60^(@)` with horizontal. A disc rolling down this inclined plane without slipping has a linear acceleration equal to
03:21View SolutionA homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
01:34View SolutionA force `F` is applied at the top of a ring of mass `M` and radius `R` placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:
 03:21View Solution
03:21View SolutionA body of radius `R` and mass `m` is rolling smoothly with speed `v` on a horizontal surface. It then rolls up a hill to a maximum height `h`. If `h = 3 v^2//4g`. What might the body be ?
03:17View SolutionA uniform rod of mass m and length l is suspended by means of two light inextensible strings as shown in figure. Tension in one string immediately after the other string is cut is
 02:59View Solution
02:59View SolutionA billiard ball of mass m and radius r, when hit in a horizontal direction by a cue at a height h above its centre, acquired a linear velocity `v_(0).` The angular velocity `omega_(0)` acquired by the ball is
02:41View SolutionThe linear velocity perpendicular to radius vector of a particle moving with angular velocity `omega=2hatK` at position vector `r=2hati+2hatj` is
01:39View SolutionABC is a right angled triangular plate of uniform thickness. The sides are such that `AB gt BC` as shown in figure. `I_(1), I_(2), I_(3)` are moments of inertia about `AB, BC` and `AC` respectively. Then which of the following relations is correct?
 02:50View Solution
02:50View SolutionA solid sphere, a ring and a disc all having same mass and radius are placed at the top of an incline and released. The friction coefficient between the objects and the incline are same but not sufficient to allow pure rolling. Least time will be taken in reaching the bottom by
02:11View SolutionIn the previous question the smallest kinetic energy at the bottom of the incline will be achieved by
03:00View SolutionA wheel of radius R rolls on the ground with a uniform velocity v. The relative acceleration of topmost point of the wheel with respect to the bottommost point is:
03:02View SolutionTwo uniform rods of equal length but different masses are rigidly joined to form an L-shaped body, which is then pivoted as shwon. If in equilibrium, the body is in the shown configuration, ratio `M//m will be
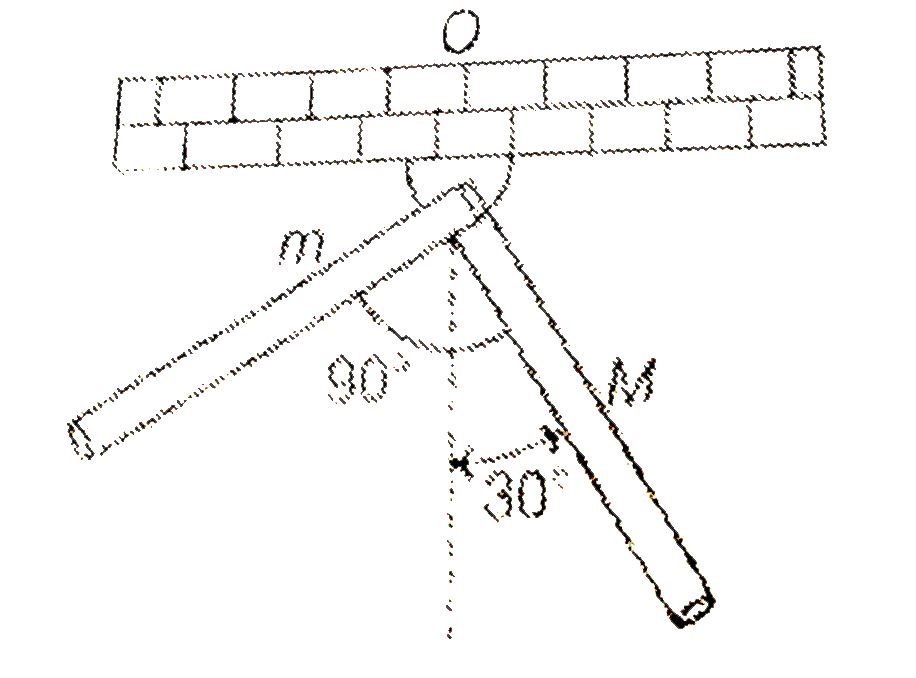 03:20View Solution
03:20View SolutionA plank with a uniform sphere placed on it resting on a smooth horizontal plane. Plank is pulled to right by a constant force `F`. If sphere does not slip over the plank. Which of the following is incorrect?
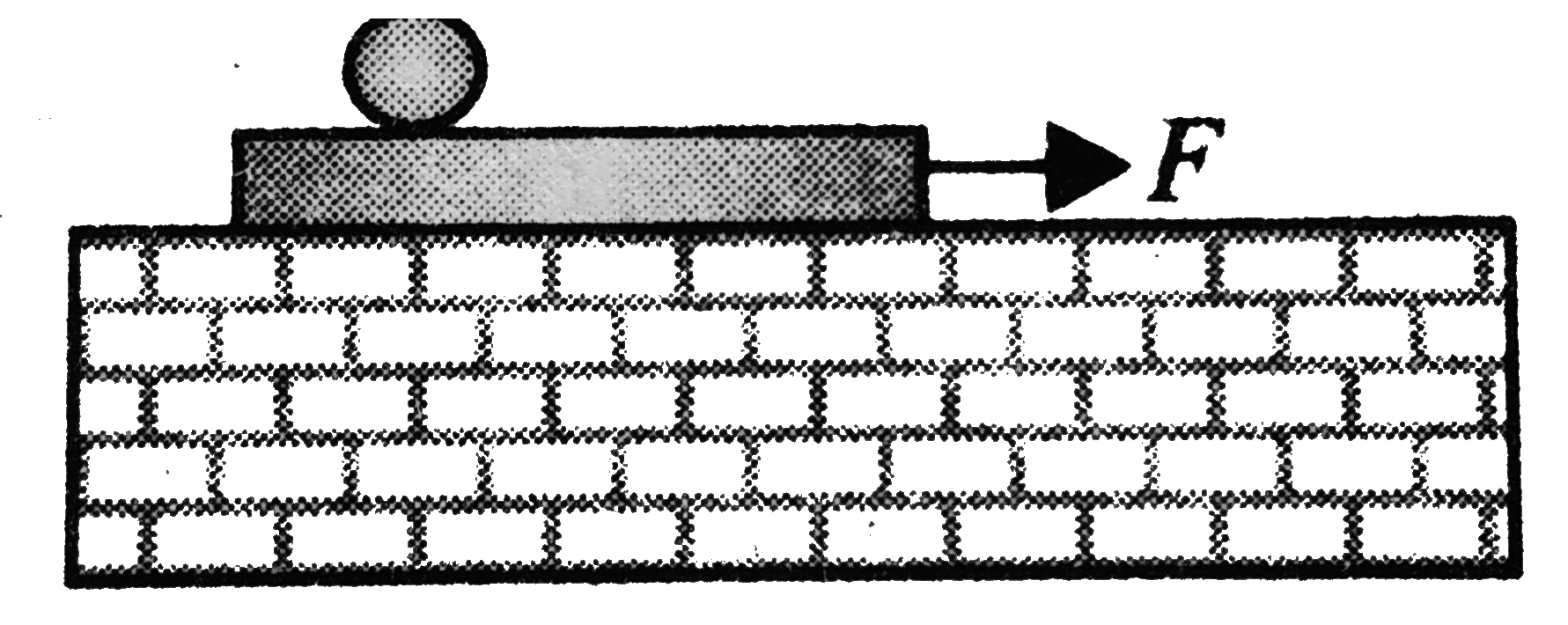 06:09View Solution
06:09View SolutionA ring mass `m` and radius `R` has three particle attached to the ring as shown in the figure. The centre of the centre `v_(0)`. Find the kinetic energy of the system. (Slipping is absent).
 .02:24View Solution
.02:24View SolutionA solid uniform sphere rotating about its axis with kinetic energy `E_(1)` is gently placed on a rough horizontal plane at time t=0, Assume that, at time `t=t_(1)`, it starts pure rolling and at that instant total KE of the sphere is `E_(2).` After sometime, at time `t=t_(2)`. KE of the sphere is `E_(3)`. Then
02:08View SolutionA solid sphere and a solid cylinder of same mass are rolled down on two inclined planes of heights `h_(1)` and `h_(2)` respectively. If at the bottom of the plane the two objects have same linear velocities, then the ratio of `h_(1):h_(2)` is
View SolutionAB and CD are two indential rods each of length L and mass M joined to from a cross. Find the M.L of the system about a bisector of the angel between the rods (XY):
 03:25View Solution
03:25View SolutionTwo cylinders having radii `2R` and `R` and moment of inertia `4I` and `I` about their central axes are supported by axles perpendicular to their planes. The large cylinder is initially rotating clockwise with angular velocity `omega_(0)`. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually slipping ceases and the two cylinders rotate at constant rates in opposite directions. During this
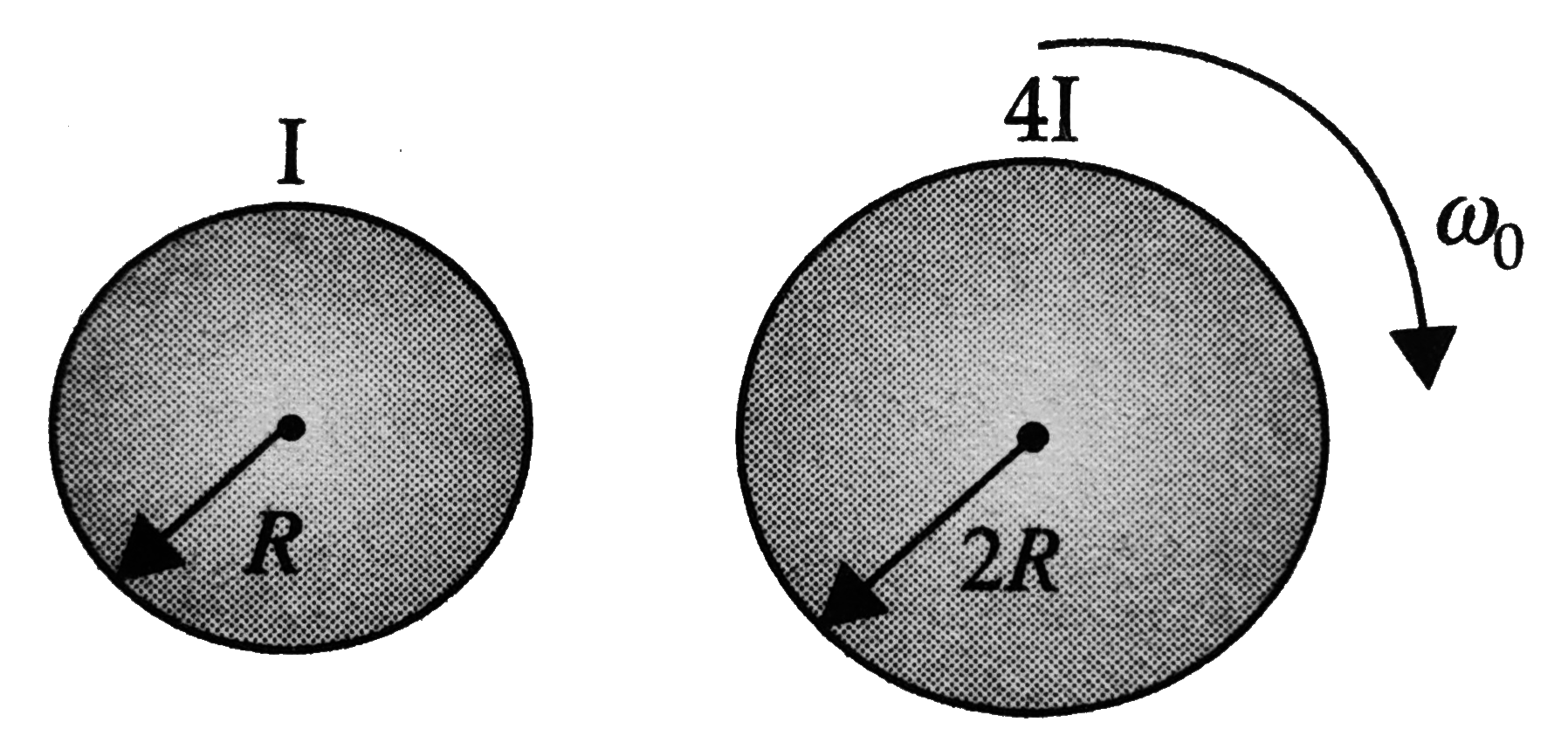 03:07View Solution
03:07View SolutionIn the above problem the final angular velocity of the small cylinder is
View SolutionA weightless rod of length `2l` carries two equal masses 'm', one tied at lower end `A` and the other at the middle of the rod at `B`. The rod can rotate in vertical plane about a fixed horizontal axis passing thriugh `C` . The rod of is released from rest in horizontal possion. The speed of the mass `B` at the instant rod become vertical is:
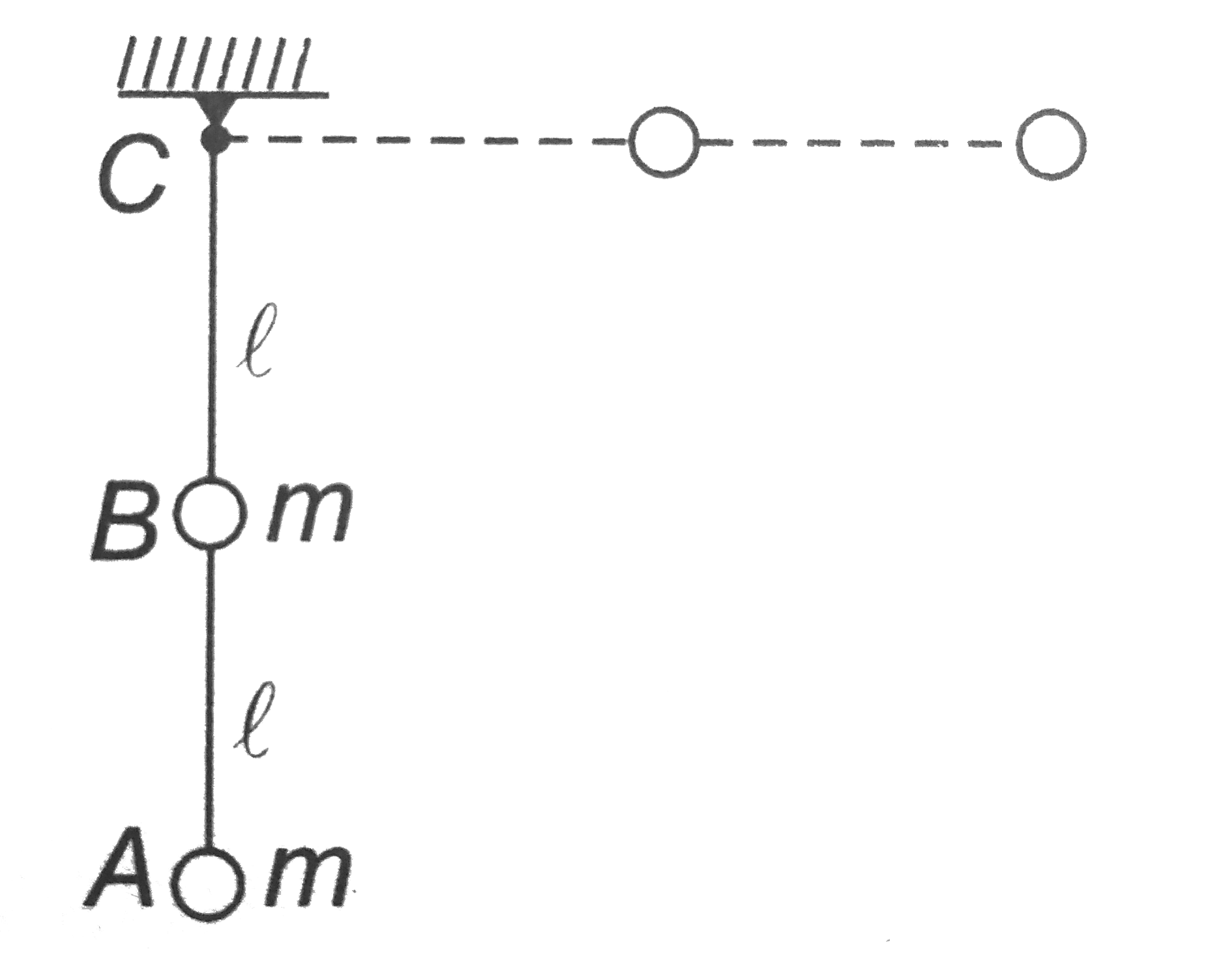 07:00View Solution
07:00View SolutionA uniform rod `AB` of mass `m` and length `l` at rest on a smooth horizontal surface . An impulse `P` is applied to the end `B`. The time taken by the rod to turn through a right angle is `:`
 02:38View Solution
02:38View SolutionThe moment of inertia of a dumb bell consisting of two identical uniform solid spheres of mass m and radius R each, joined by a thin metallic rod of equal mass m (separation between the centres of the spheres is 6R) is I about the axis AB. Its moment of inertia, about an axis making an angle of `45^(@)` with AB, is
 03:08View Solution
03:08View SolutionA uniform rod of mass 2M is bent into four adjacent semicircles each of radius r, all lying in the same plane. The moment of inertia of the bent rod about an axis through one end A and perpendicular to plane of rod is
 View Solution
View SolutionA ring of mass m is rolling without slipping with linear velocity v as shown is figure. A rod of identical mass is fixed alone one of its diameter. The total kinetic energy of the system is
 01:55View Solution
01:55View SolutionA disc is given an angular velocity `omega_(0)` and a linear velocity `v_(0)` as shown in the figure. It is released on a rough horizontal surface of friction coefficient `mu.` Mark the correct statement `(omega_(0)=3v_(0)//R)`
 View Solution
View SolutionA string is wrapped on a uniform disc and the other end of the string connected to a wall. The system is placed on a smooth plane, inclined at an angle `theta`, with the string parallel to the plane, as shown in the figure. The acceleration of the disc is
 View Solution
View SolutionIn the figure shown a smooth ring is connected to rod AB, while rod CD passes through ring. At the given instant angular velocity of rod AB about hinge A is 1 `rod//s` and AC=CB. Instantaneous angular velocity of rod CD about hinge C is
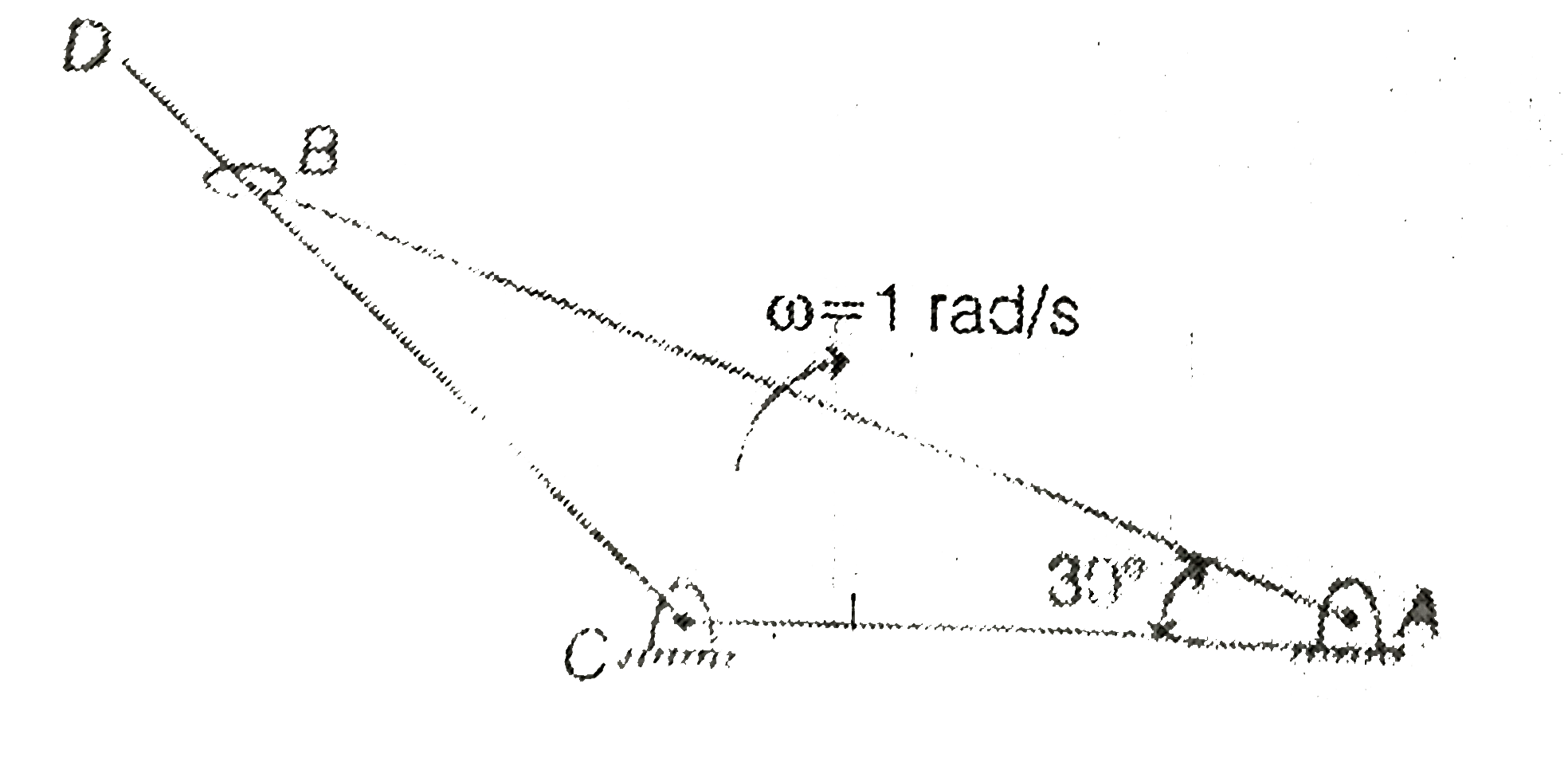 View Solution
View SolutionConsider the moment of inertia I of the rigid homogerneous disc of mass M as shown in the figure about an axis through its centre (different shadings only differentiate the two parts of the disc each with equal mass `M//2`). Which one of the following statements concerning I is correct?
 View Solution
View Solution
JEE Main questions and complete solutions for chapter ROTATIONAL MOTION of DC PANDEY PHYSICS (HINGLISH) of Class 11
