Complete Solutions to A Only One Option is Correct of chapter ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MOTION |
| DC PANDEY MASTER PROBLEM PACKAGE | A Only One Option is Correct |
| Number Of Questions | 86 |
| Academic Year | 2023-24 |
A solid sphere and a hollow sphere of equal mass and radius are placed over a rough horizontal surface after rotating it about its mass centre with same angular velocity `omega_(0)`. Once the pure rolling starts let `v_(1)` and `v_(2)` be the linear speeds of their centres of mass. Then
05:38View SolutionIn the above problem, if coefficient of friction for both the spheres is same and let `t_(1)` and `t_(2)` be the times when pure rolling of solid sphere and of hollow sphere is started. Then
View SolutionA ball of mass `m` and radius `r` rolls inside a hemispherical shell of radius `R`. It is released from rest from point `A` as shown in figure. The angular velocity of centre of the ball in position `B` about the centre of the shell is.
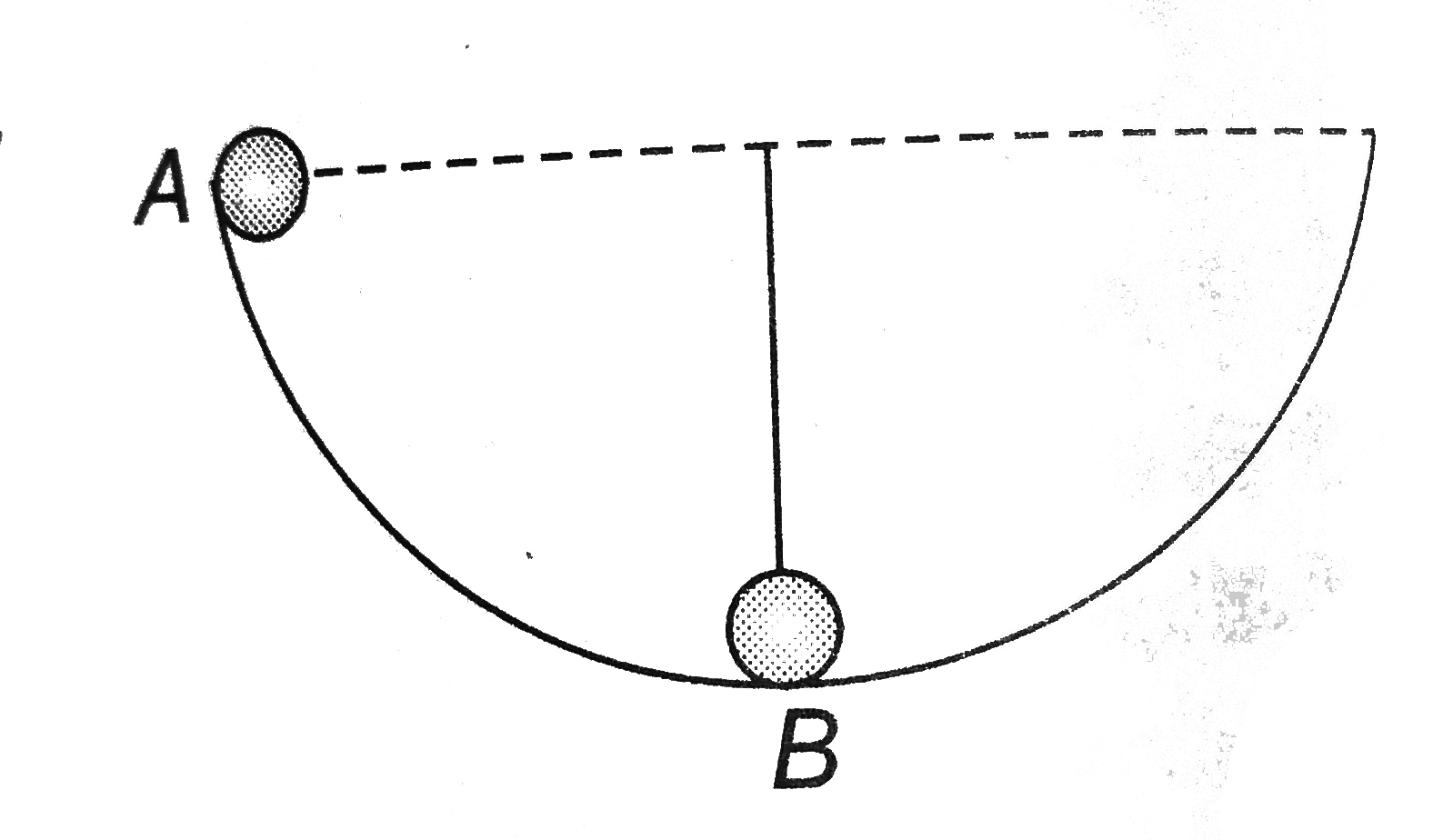 .07:29View Solution
.07:29View SolutionIn the above probllem, the normal force between the ball and the shell in position B is (m=mass of ball)
View SolutionA disc of radius 0.1 mrolls without sliding on a horizontal suirface with a velocity of 6 m`//`s. It then ascends a smooth continous track as shown in figure. The height upto which it will ascend is (g=`10 m//s^(2)`)
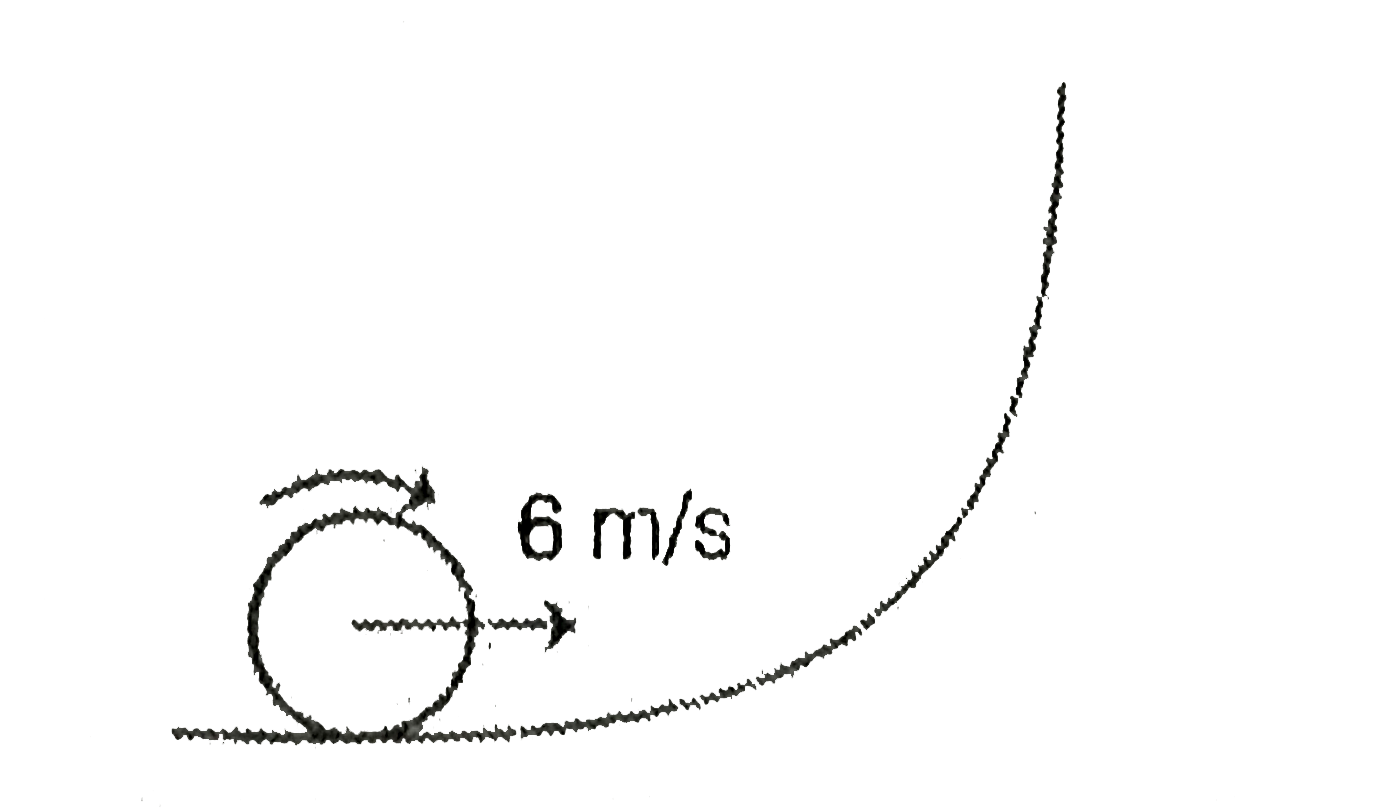 View Solution
View SolutionA uniform cylinder of mass `M` and radius `R` rolls without slipping down a slope of angle 8 with horizontal. The cylinder is connected to a spring of force constant `k` at the centre, the other side of which is connected to a fixed support at A. The cylinder is released when the spring is unstretched. The· force of friction `(f)`:
 01:48View Solution
01:48View SolutionA spool of mass `M` and radius `2R` lies on an inclined plane as shown in the figure. A light thread is wound around the connecting tube of the spool and its free end carries a weight of mass `m`. The value of `m` so that system is in equilibrium is
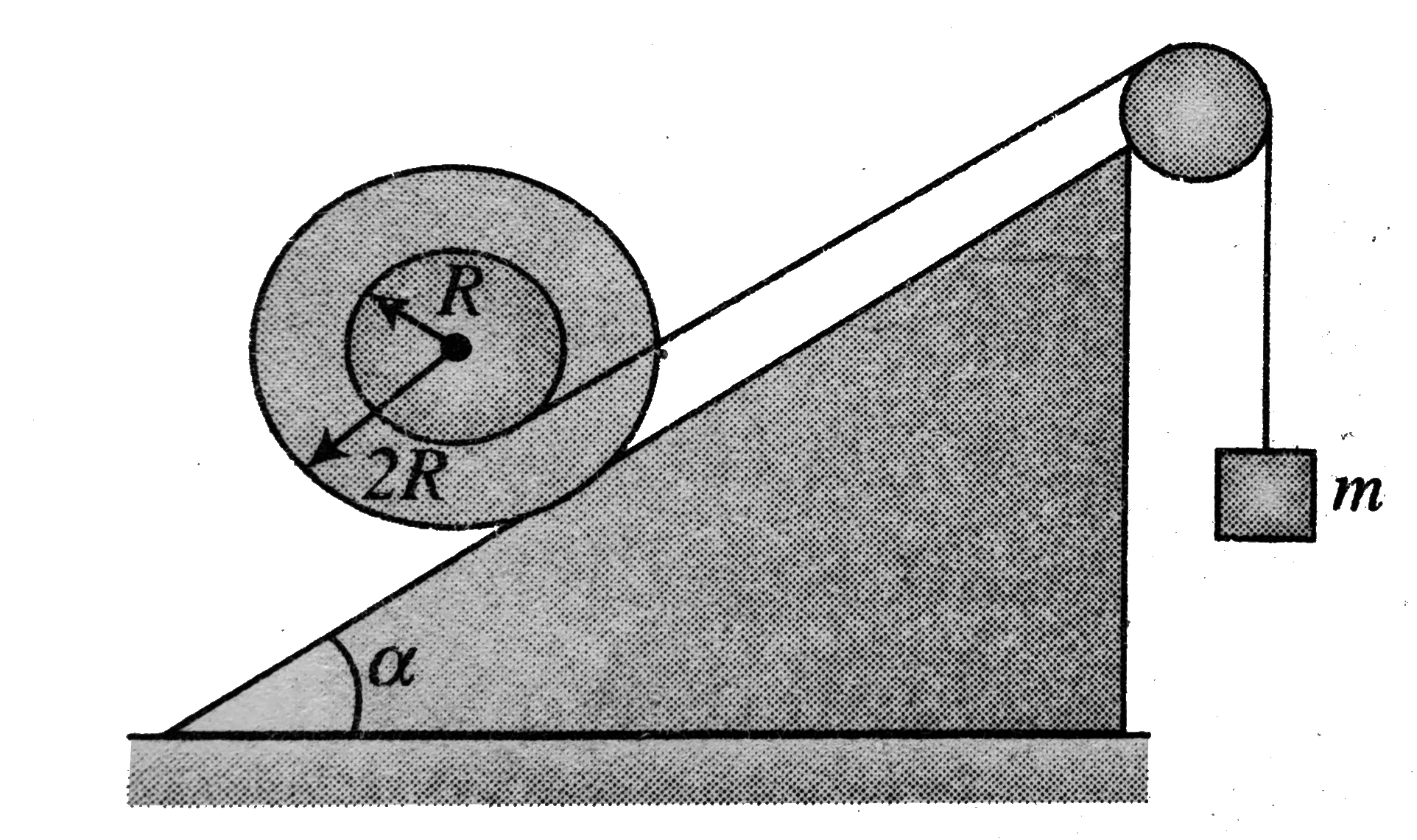 03:51View Solution
03:51View SolutionIn both the figures all other factors are same, except that in figure (i) `AB` is rough and `BC` is smooth while in figure (ii) `AB` is smooth and `BC` is rough. In figure (i), if a sphere is released from rest it starts rolling. Now consider the figure (ii), if same sphere is A released from top of the inclined plane, what will be the kinetic energy of the sphere on reaching the bottom:
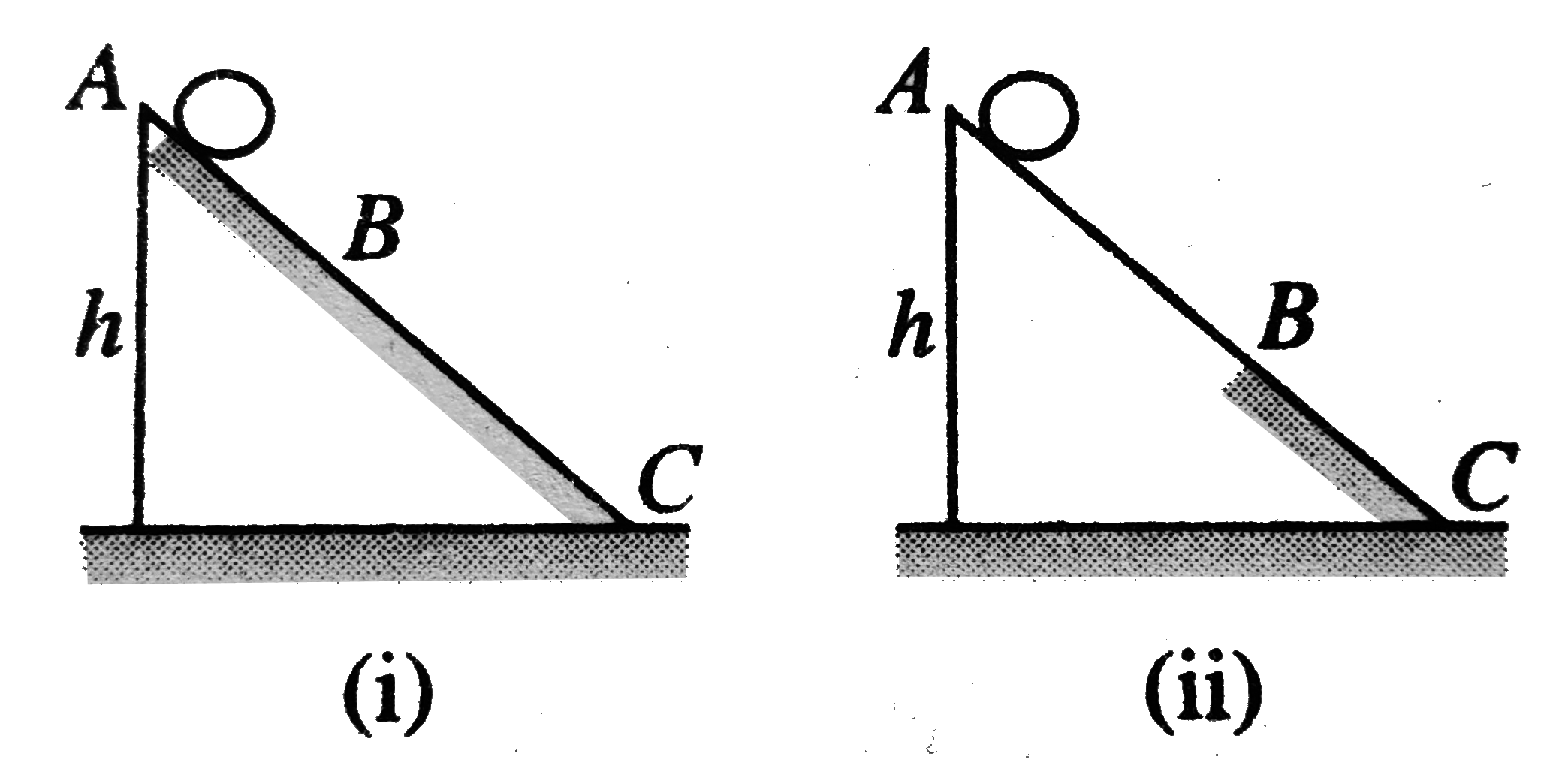 05:31View Solution
05:31View SolutionA ring of radius `R` is first rotated with an angular velocity `omega` and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is `mu`. Time after which its angular speed is reduced to half is
03:44View SolutionA rod of length l is given two velocities `v_(1)` and `v_(2)` in opposite directions at its two ends at right angles to the length. The distance of the instantaneous axis of rotation from `v_(1)` is
View SolutionTwo particles connected by a rigid light rod AB, lying on a smooth horizontal table. An impulse J is applied at A in the plane of thetable and perpendicular at AB. Then the velocity of particle at A is
View SolutionA disc of radius r rolls without slipping on a rough horizontal floor. If veloocity of its centre of mass is `v_(0)`, then velocity of point P, as shown in the figure
(OP=r`//`2 and `angleQOP=60^(@)`)is
 View Solution
View SolutionA flat rail road car is accelariting along the positive x-axis with an acceleration `a_(p)`. A sphere is placed over the car. The friction between the car and the sphere is not sufficent to support pure rolloing of sphere. The correct statement is
View SolutionA uniform ring of mass m and radius R is released from top of an inclined plane. The plane makes an angle `theta` with horizontal. The cofficent of friction between the ring and plane is `mu`. Initially, the point of contact of ring and plane is P. Angular momentum of ring about an axis passing from point P and perpendicular to plane of motion as a function of time t is
View SolutionA wheel ios rolling without sliding on a horizontal surface. The centre of the wheelk moves with a constant speed `v_(0)`. Consider a point P on the rim which is at the top at time t=0. The square of speed of point P is plooted against time t. The correct plot is (R is radius of the wheel)
View Solutiona uniform circular disc of radiu8s r placed on a roughn horizontal plane has initial velocity `v_(0)` and an angul,ar velocity `omega_(0)` has shown The disc comes to rest after moving some distance in the direction of motion. Then
 View Solution
View SolutionA solid sphere of radius R is resting on a smooth horizontal surface. A constant force F is applied at a height h from the bottom. Vhoose the correct alternative.
 View Solution
View SolutionFour holes of radius `R` are cut from a thin square plate of side `4 R` and mass `M`. The moment of inertia of the remaining portion about z-axis is :
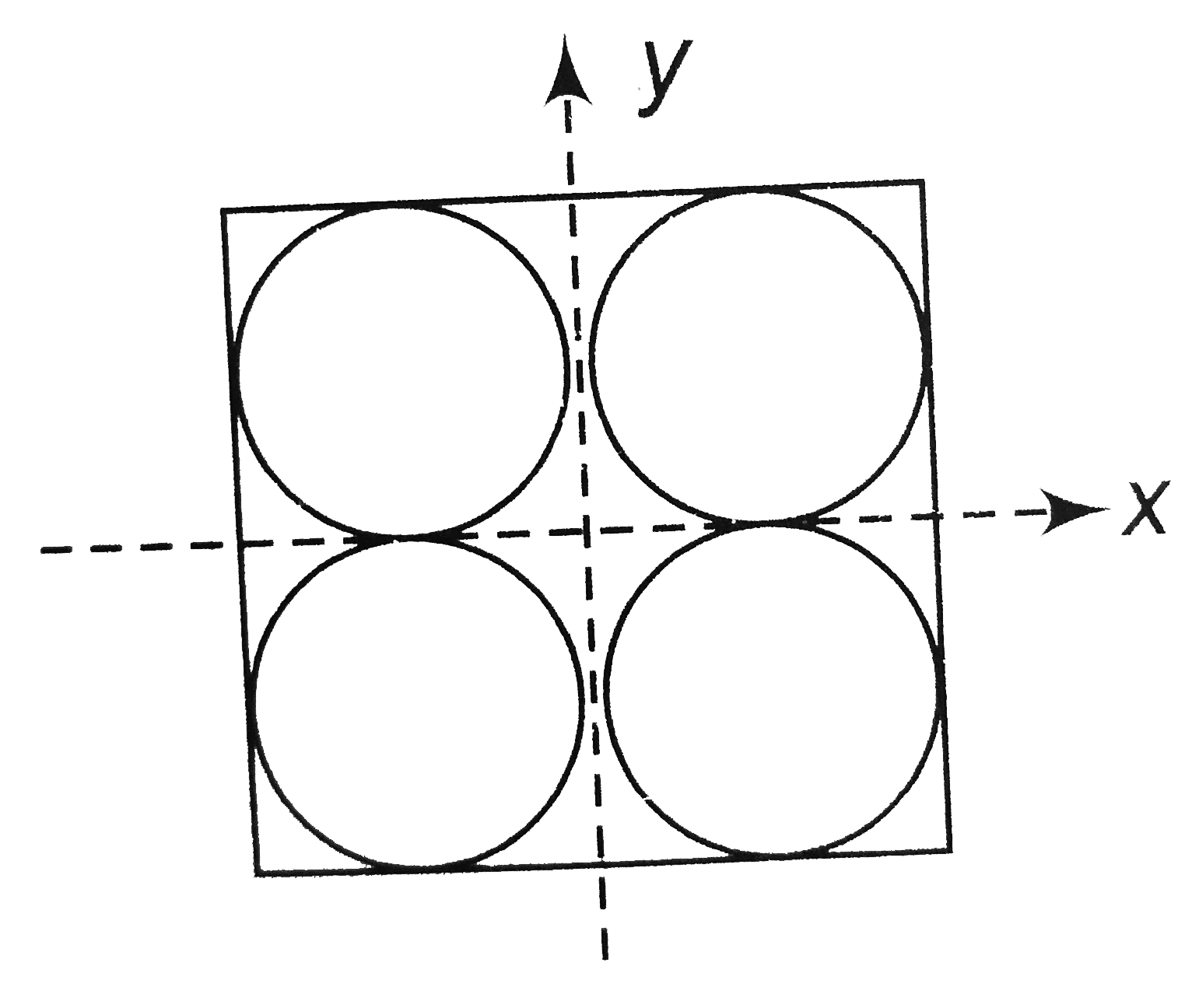 .05:39View Solution
.05:39View SolutionA wire of mass m and length l is bent in the form of a quarter circle. The moment of the inertia of the wire about an axis is passing through the centre of the quarter circle is approximately
View SolutionA uniform disc of radius R lies in x-y plane with its centre at origin. Its moment of inertia about the axis x=2R and y=0 is equal to the moment of inertia about the axis y=d and z=0, where d is equal to
View SolutionTwo rods OA and OB of equal length and mass are lying on xy plane as shown in figure. Let `I_(x),I_(y)` and `I_(z)` be the moment of inertia of both the rods bout x,y and z axis respectively. Then,
 View Solution
View SolutionA wire of length l and mass m is first bent in a circle, then in a square and then in an equilateral triangle. The moment of inertia in these three cases about an axis perpendicular to their planes and passing through their centrer of mass are `I_(1),I_(2)` and `I_(3)` respectively. Then maximum of them is
View SolutionA disc of radius `R` rolls on a horizontal ground with linear acceleration `a` and angular acceleration `alpha` as shown in Fig. The magnitude of acceleration of point `P` as shown in the figure at an instant when its linear velocity is `v` and angular velocity is `omega` will be a
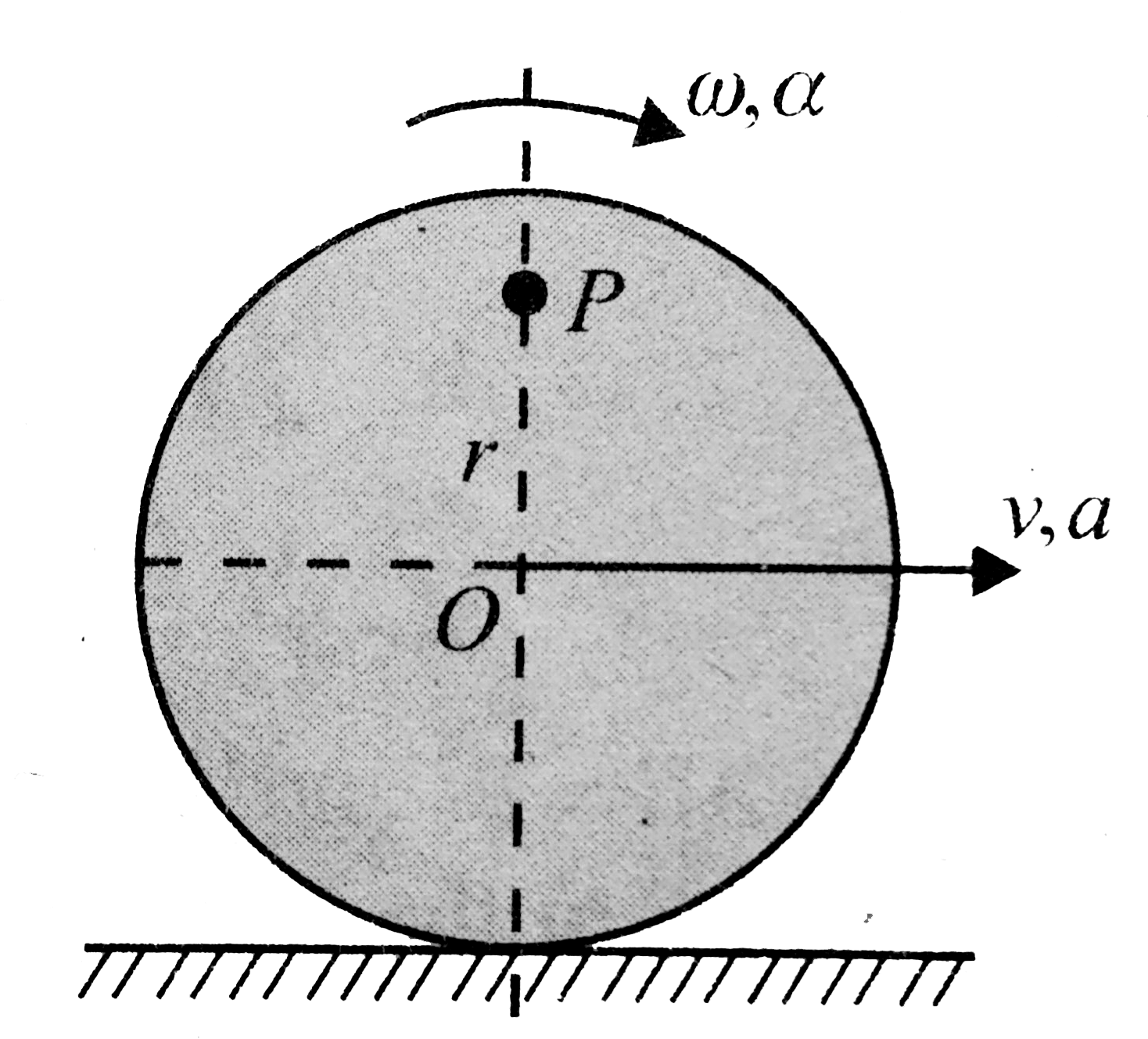 02:46View Solution
02:46View SolutionA rod of length l slided down along the inclined wall as shown in figure. At the instant shown in figure, the speed of end A is v, then the speed of B will be
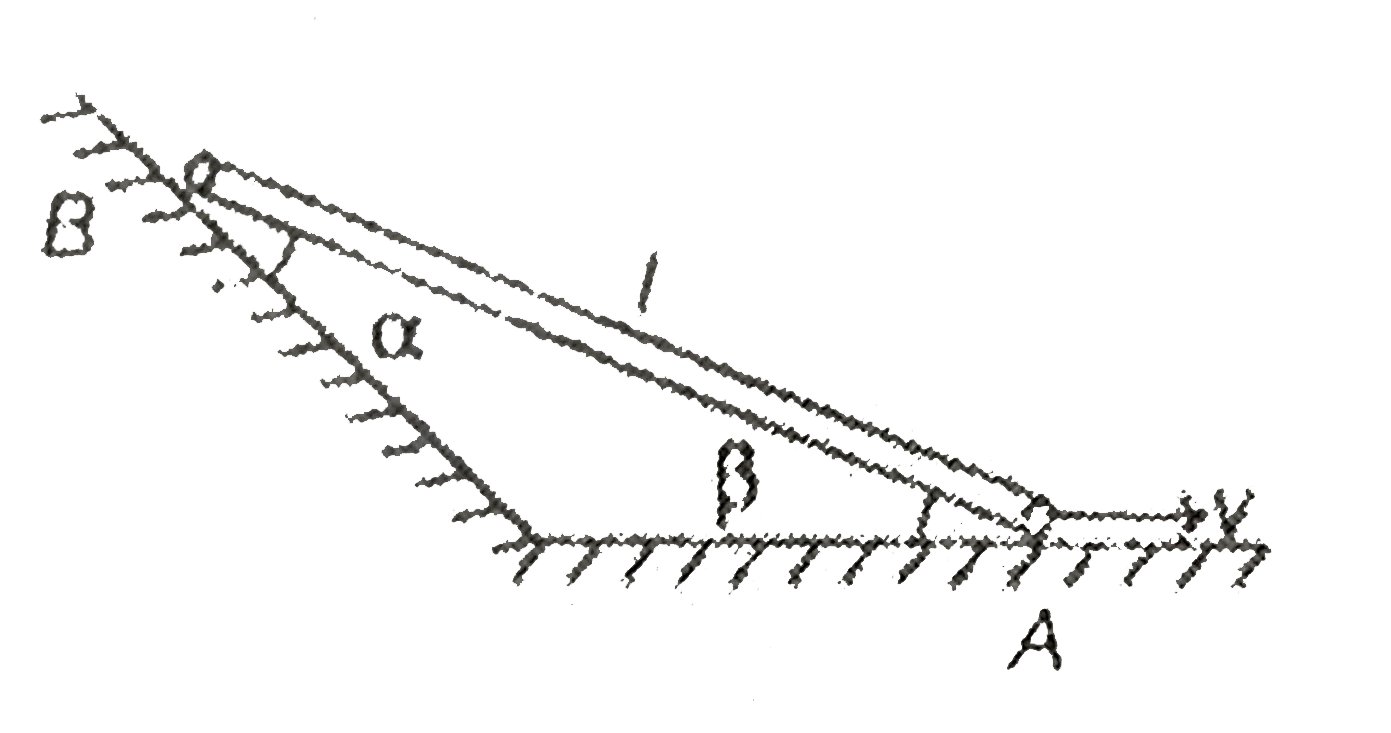 View Solution
View SolutionA disc of radius `R` rolls without slipping at speed `v` along positive `x`-axis. Velocity of point `P` at the instant shown in Fig. is
 02:18View Solution
02:18View SolutionTwo particles `A` and `B` are situated at a distance `d = 2m` apart. Particle `A` has a velocity of `10 m//s` at an angle of `60^@` and particle `B` has a velocity `v` at an angle `30^@` as shown in figure. The distance `d` between `A` and `B` is constant. the angular velocity of `B` with respect to `A` is :
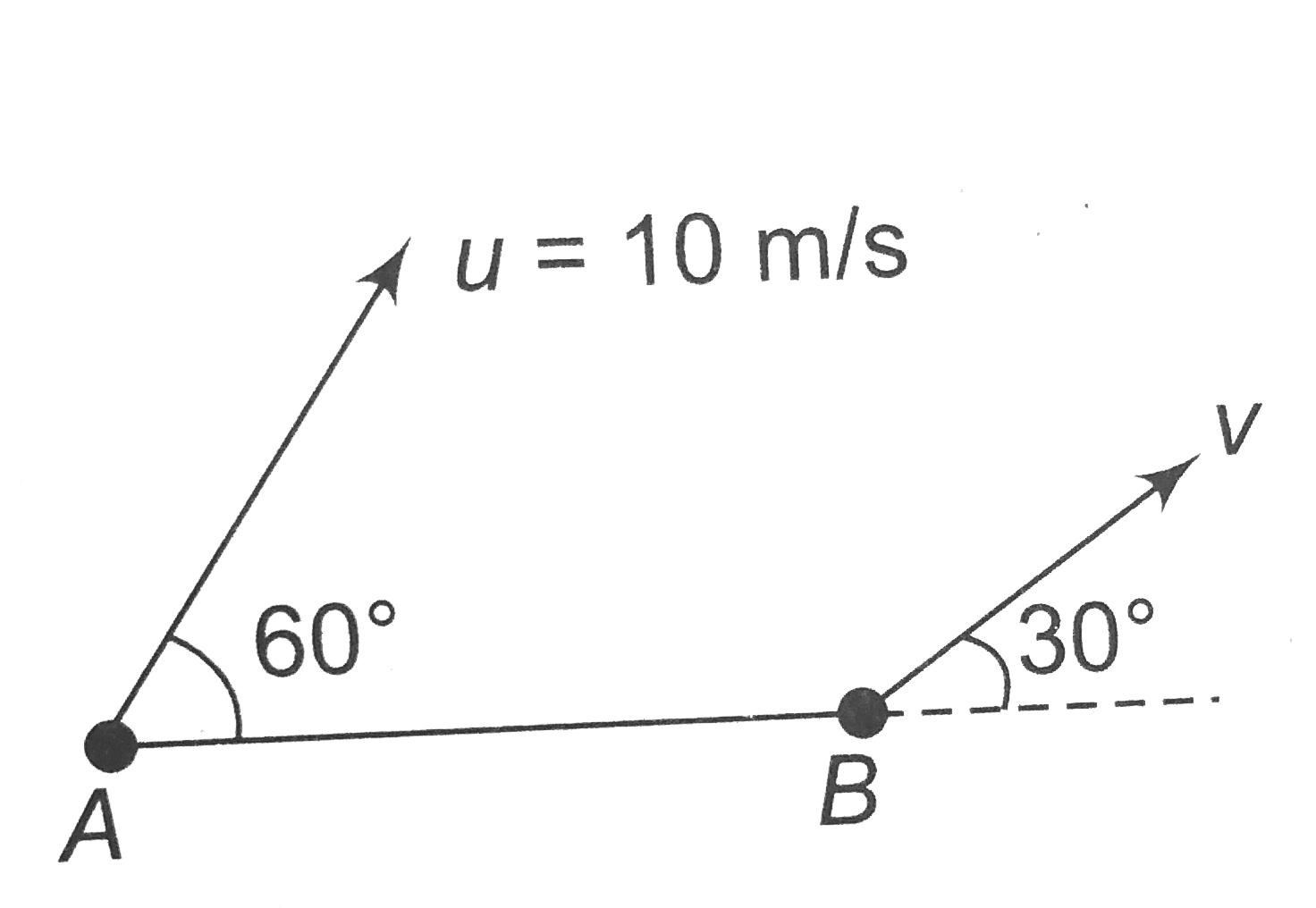 .03:34View Solution
.03:34View SolutionA force `F` is applied on the top of a cube as shown in the figure. The coefficient of friction between the cube and the ground is `mu`. If `F` is gradually increased, find the value of `mu` for which the cube will topple before sliding.
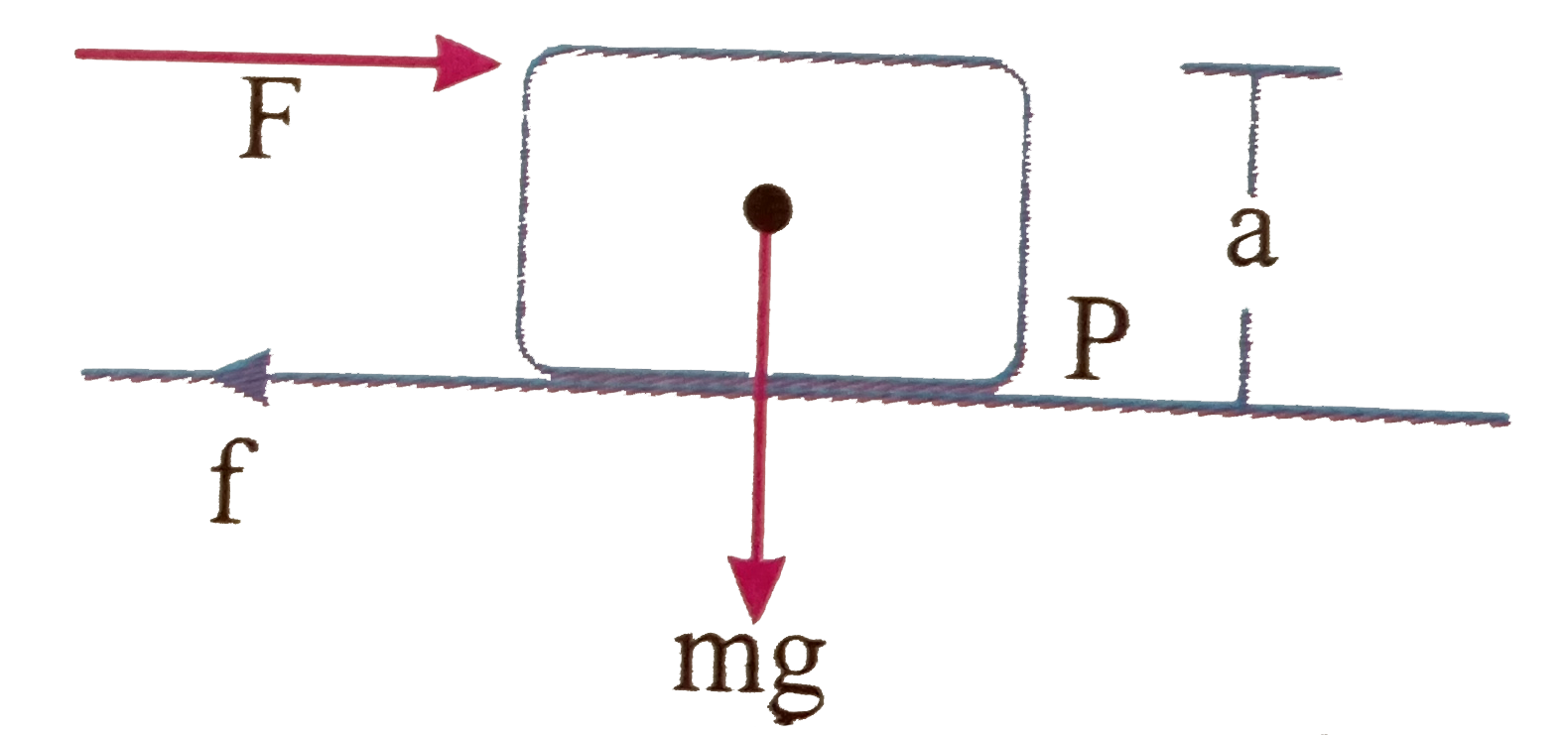 02:03View Solution
02:03View SolutionA cube is pplaced on an inclined plane of inclinbation `theta` as shown in figure. Cofficent of friction br=etween the cube and the plane is `mu`. As the angle `theta` is gradually increased, the cube slides before toppling if
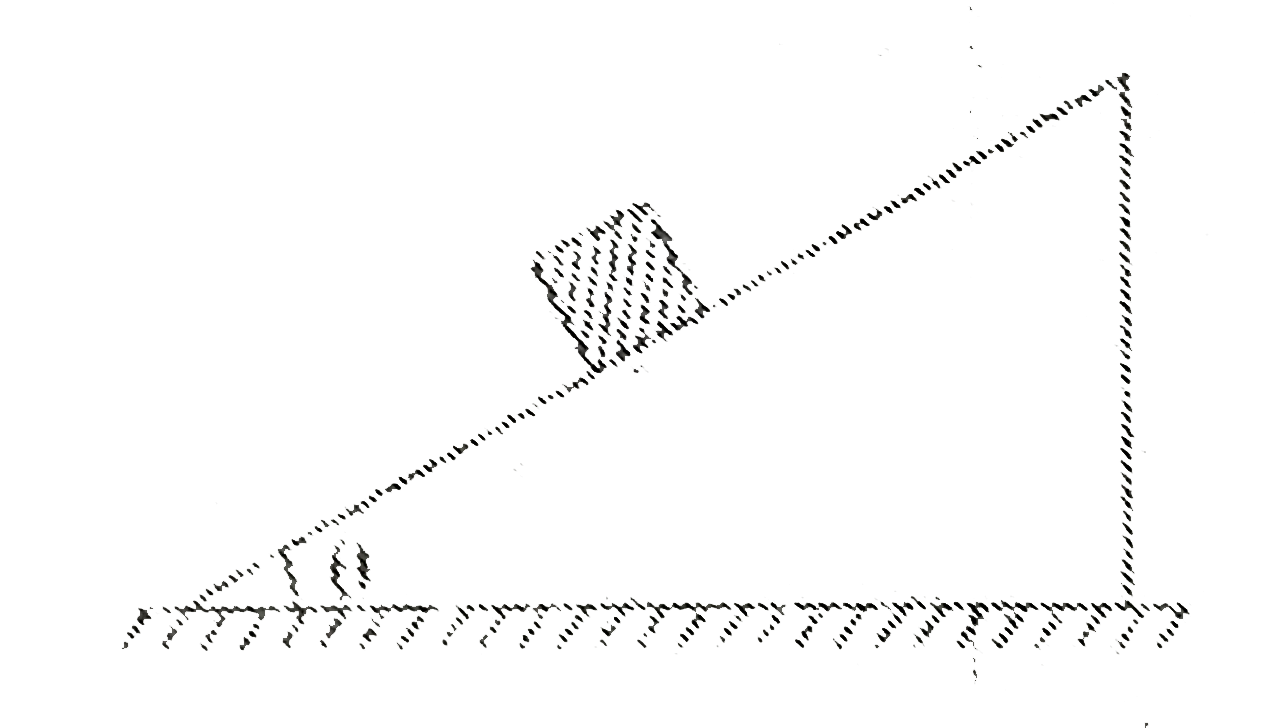 View Solution
View SolutionA uniform rod `AB` of mass `m` and length `l` is at rest on a smooth horizontal surface. An impulse `J` is applied to the end `B`, perpendicular to the rod in the horizontal direction. Speed of particlem `P` at a distance `(l)/(6)` from the centre towards `A` of the rod after time `t = (pi m l)/(12 J)` is.
04:15View SolutionA horizontal turn table in the form of a disc of radius `r` carries a gun at `G` and rotates with angular velocity `omega_(0)` about a vertical axis passing through the centre `O`. The increase in angular velocity of the system if the gun fires a bullet of mass `m` with a tangential velocity `v` with respect to the gun is (moment of inertia of gun `+` table about `O` is `I_(0)`
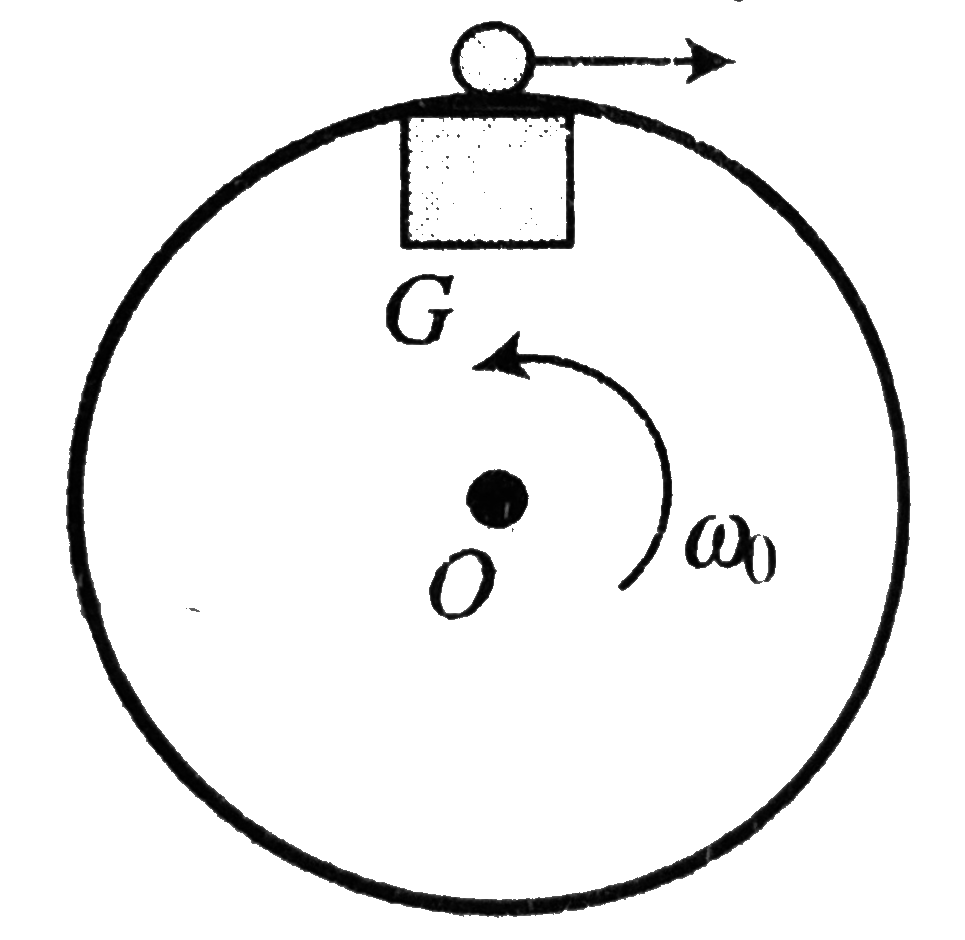 06:57View Solution
06:57View SolutionAverage torque on a projectile of mass `m` (initial speed `u` and angle of projection `theta`) between initial and final positions `P` and `Q` as shown in figure, about the point of projection is :
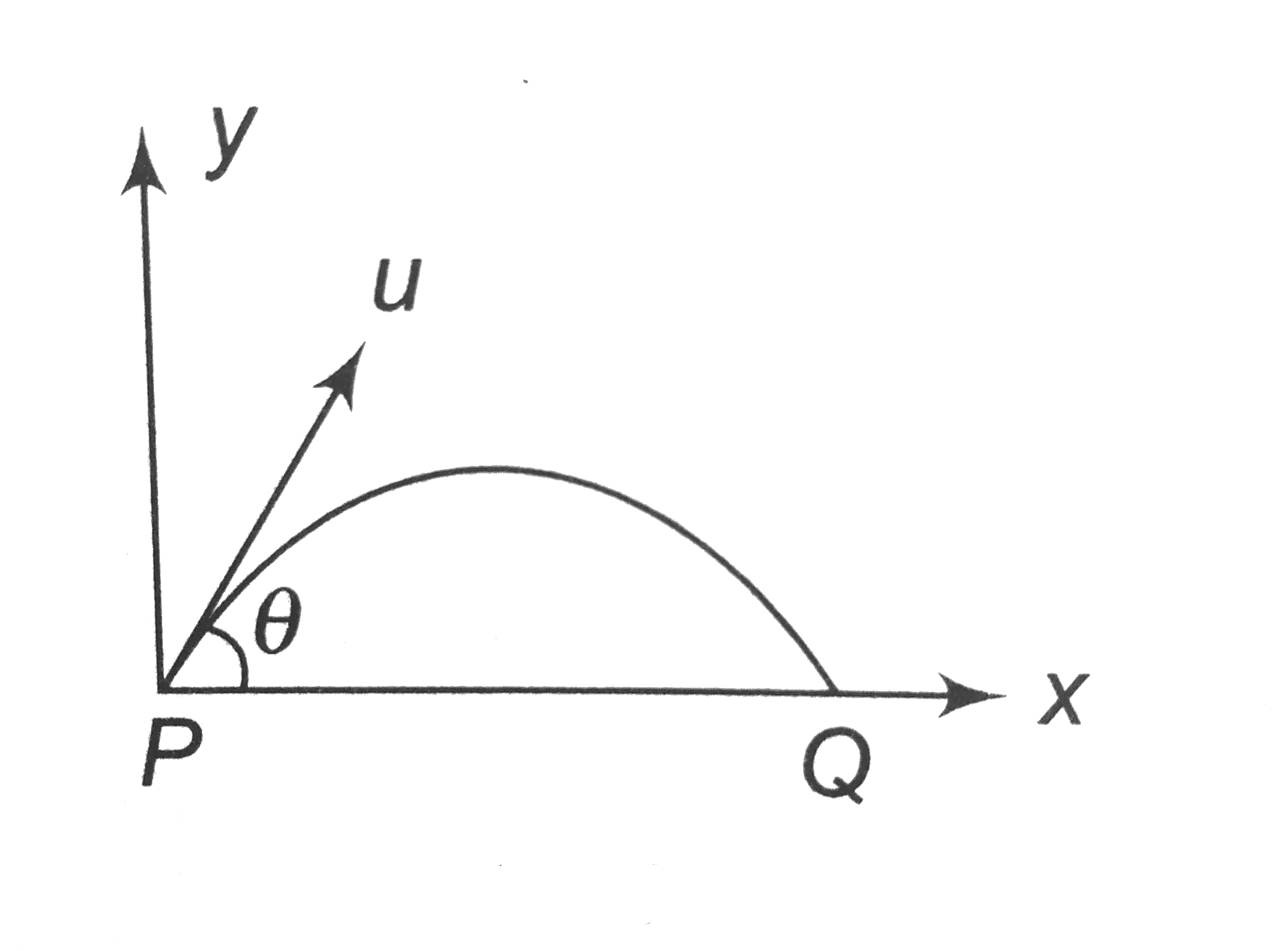 .03:04View Solution
.03:04View SolutionA uniform rod AB of mass m and length 2a is falling freely without rotationb under gravity with AB horizontal. Suddenly the end A is fixed when the speed of the rod is v. The angular speed which the rod begains to rotate is
View SolutionFigures shows a smooth inclined plane of inclination `theta` fixed ina car. A sphere is set in pure rolling on the incline. For what value of a (the acceleration of car in horizontal direction) the sphere will continue pure rolling ?
 View Solution
View SolutionThe acceleration a of the plank P required to keep the centre C of a cylinder in a fixed position during the motion is (no slipping take place between cylinder and plank)
 View Solution
View SolutionA spherical body of radius R is allowed to roll down on an incline with out slipping and it recheas with a speed `v_(0)` at the bottom. The incline is then made smooth by waxing and the body is allowed top slide without rolling and now the speed attained is `(5)/(4)v_(0)` The radius of gyration of the body about an axis passing through the centre is
View SolutionPortion AB of the wedge shown in figure is rough and Bc is smooth. A solid cylinder rolls without spinning from A to B. If AB=BC, then ratio of transitional kinetic energy to rotational kinetic energy, when the cylinder reaches point C is
 View Solution
View SolutionOne end of a uniform rod of length l and mass m is hinged at A. It is released from the rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes verticle is
 View Solution
View SolutionA sphere is rotating between two rough inclined walls as shoen in fiogure. Cofficent of friction between each wall and the sphere is `(1)/(3)`. If `f_(1)` and `f_(2)` be the ffriction forces at PO and Q. Then `(f_(1))/(f_(2))` is
 View Solution
View SolutionA rod of mass m and length l is hinged at one of its end A as shown in figure. A force F is applied at a distance x from A. The acceleration of centre of mass a varies with x as
 View Solution
View SolutionA uniform rod of length l is pivoted at point A. It struk n=by an horizontal force which delivers an ikmpulse J at a distance c from point A as shown in figure. Impulse delivered by pivot is zero, if x is equal to
 View Solution
View SolutionA thin uniform rod of mass m moves translationally with acceleration a due to two antiparallel forces of lever arm l. One force is of magnitude F and acts at one extreme end. The length of the rod is
View SolutionIn the figure shon mass of both, the spherical body and blocks is m. Moment of inertia of the spherical body about centre of mass is `2mR^(2)`. The spherical body rolls on the horizontal surface. There is no sliiping between any two surfaces in contact. The ratio of kinetic energy of the spherical body to that of block is
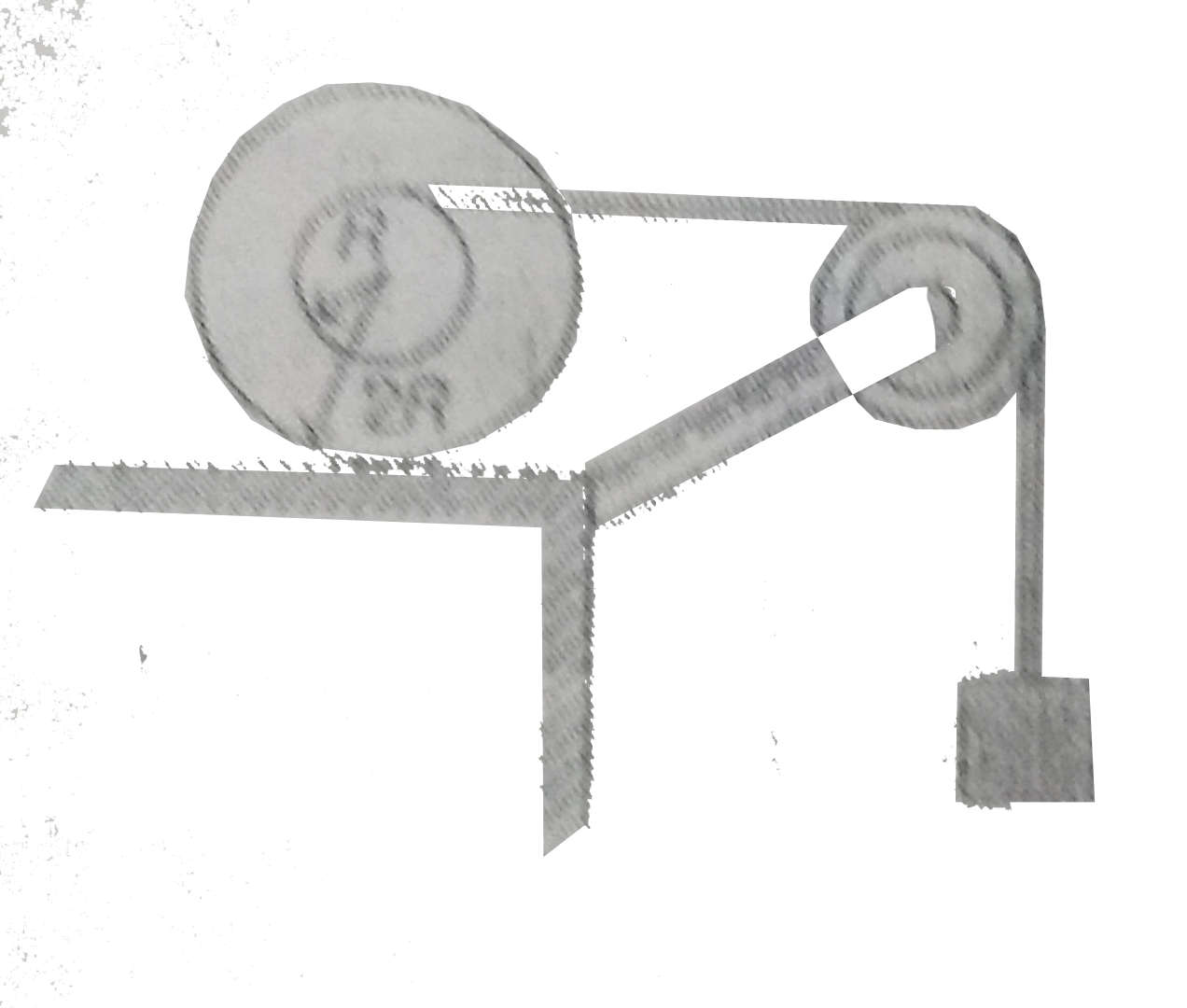 View Solution
View SolutionA particle is projected with velocity v at an angle `theta` aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
01:33View SolutionAn impulse `J` is applied on a ring of mass `m` along a line passing through its centre `O`. The ring is placed on a rough horizontal surface. The linear velocity of centre of ring once it starts rolling without slipping is
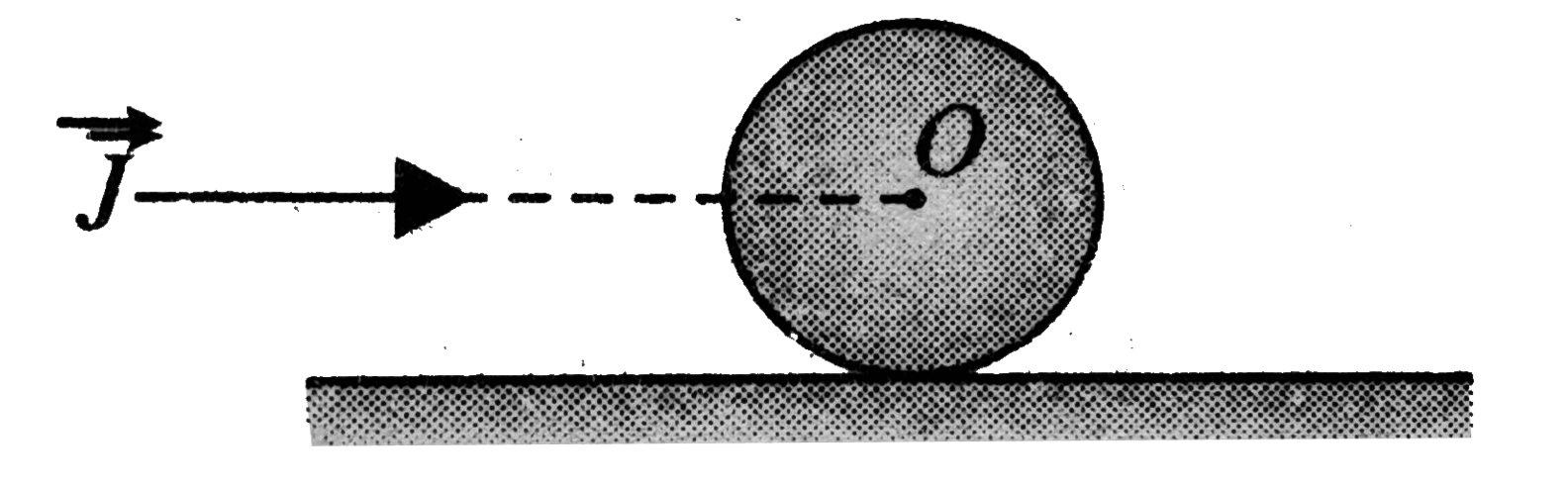 06:06View Solution
06:06View SolutionA plank of mass `M` is placed over smooth inclined plane and sphere is also placed over the plank. Friction is sufficient between sphere and plank. If plank and sphere are released from rest, the frictional force on sphere is -
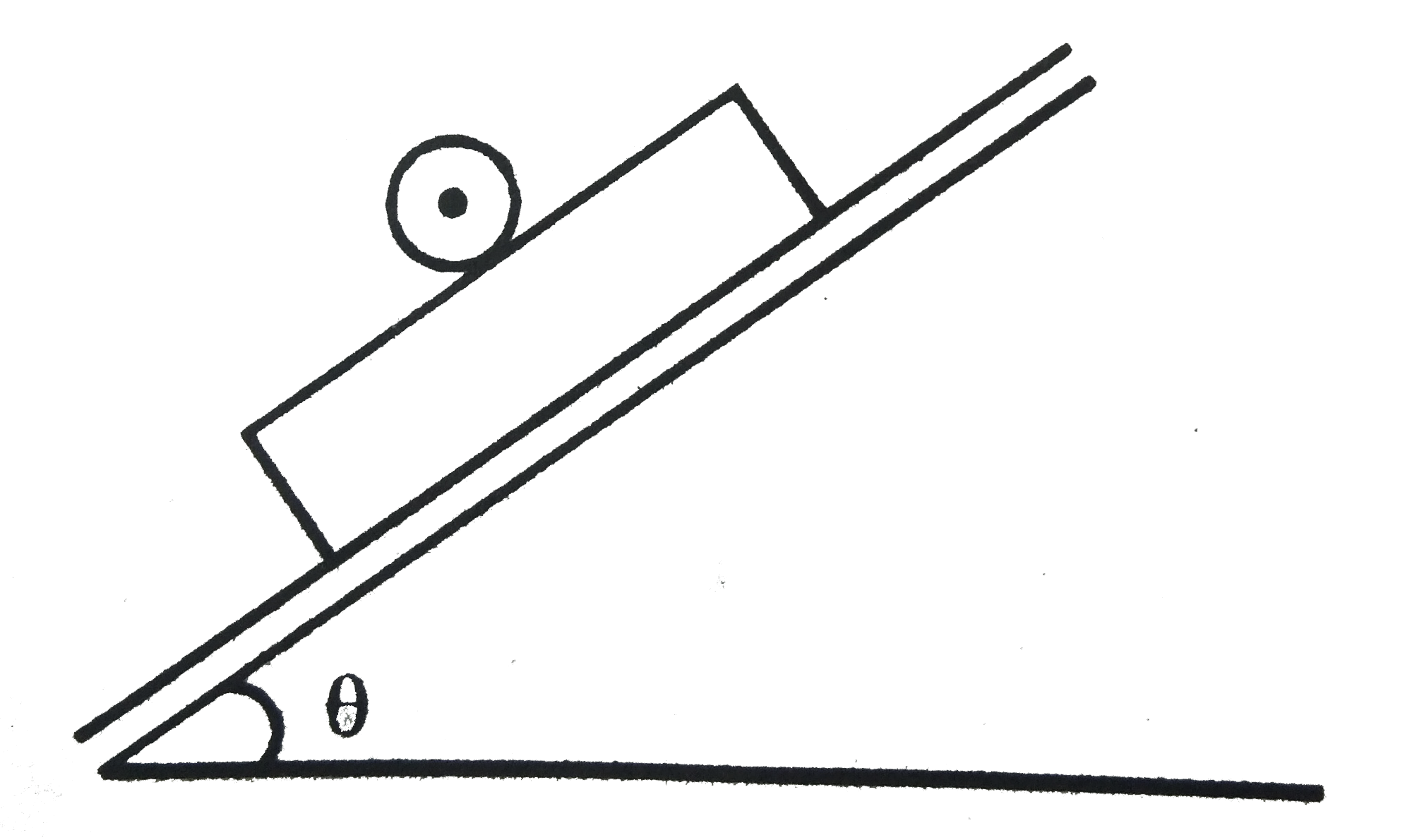 .03:26View Solution
.03:26View SolutionIn the figure shown, the plank is being pulled to the right with a constant speed `v`. If the cylinder does not slip then:
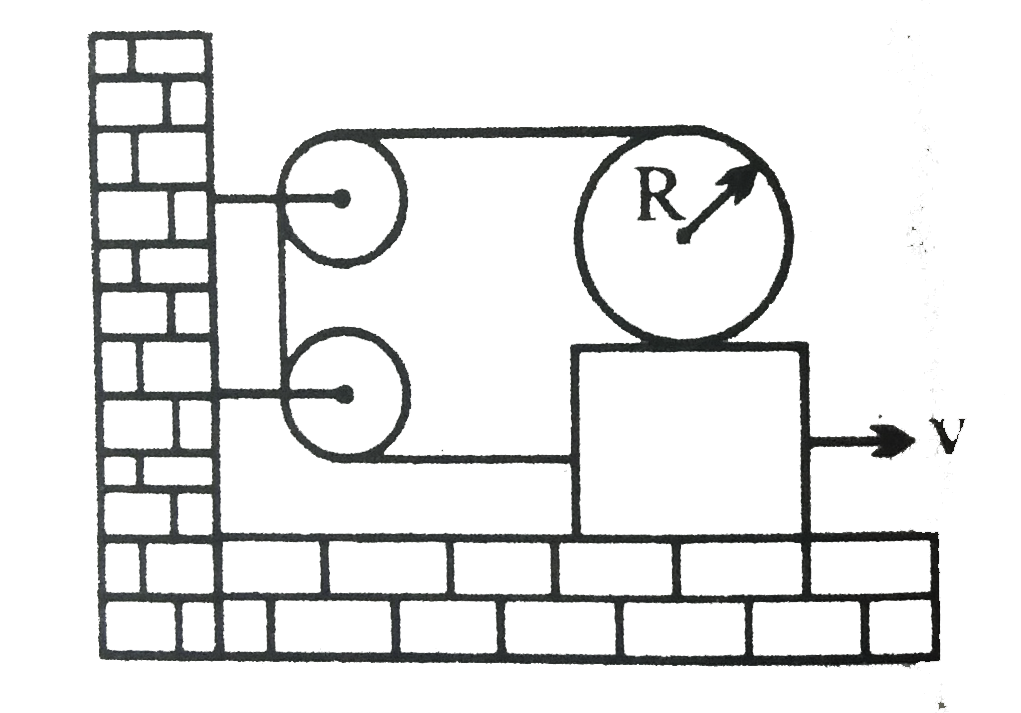 .04:21View Solution
.04:21View SolutionA uniform rod `AB` of length `L` and mass `M` is lying on a smooth table. A small particle if mass `m` strike the rod with velocity `v_(0)` at point `C` at a distance comes to rest after collision. Then find the value of `x`, so that point `A` of the rod remains stationary just after collision.
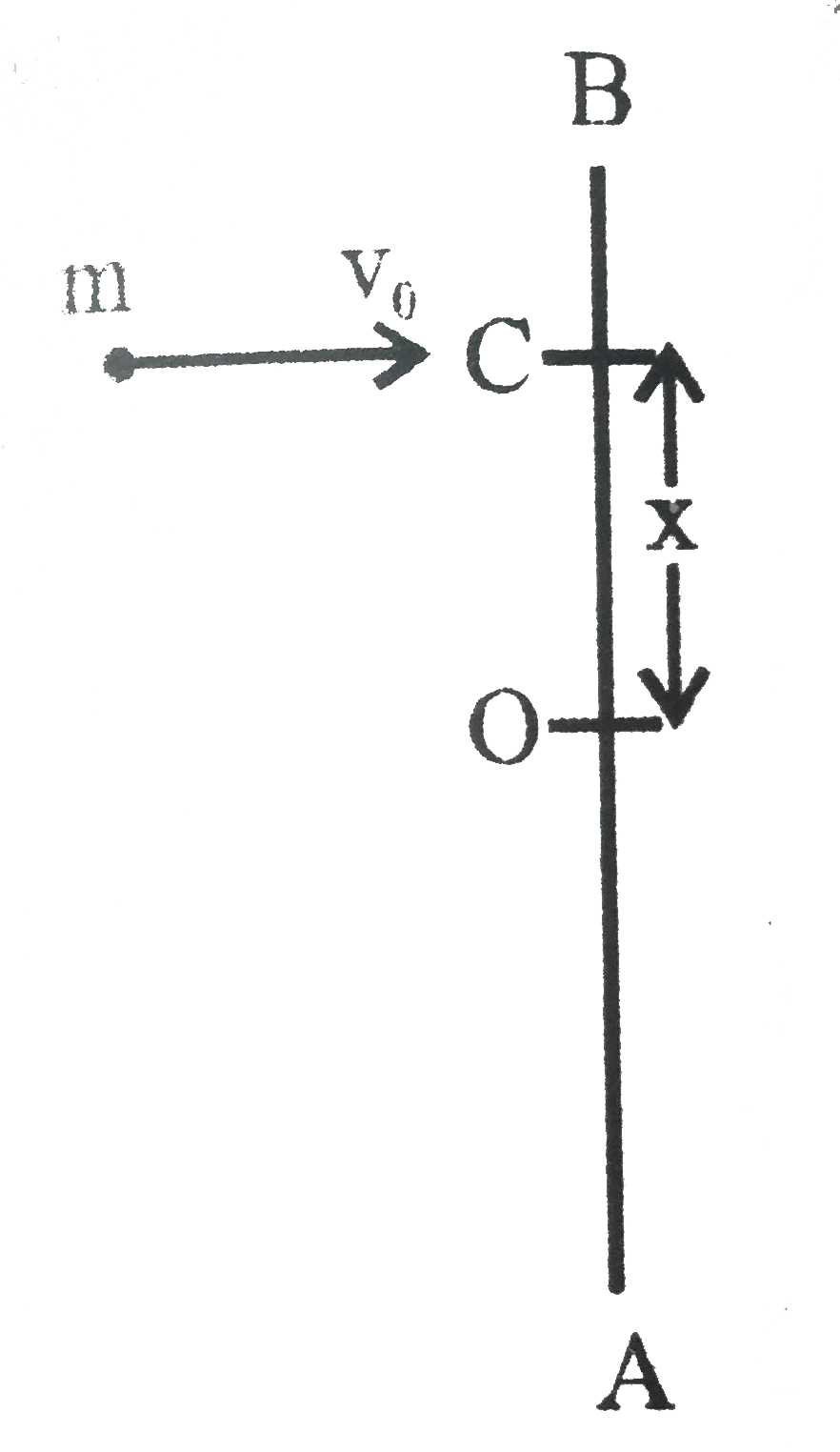 .04:49View Solution
.04:49View SolutionA time varying force F=2t is applied on a spool as shown in figure. The angular momentum of the spool at time t about bottommost point is
 01:04View Solution
01:04View SolutionA right triangular plate ABC of mass m is free to rotate in the verticle plane about a fixed horizontal axis through A. It is supported by a string such that the side AB is horizontal. The reaction at the support A is
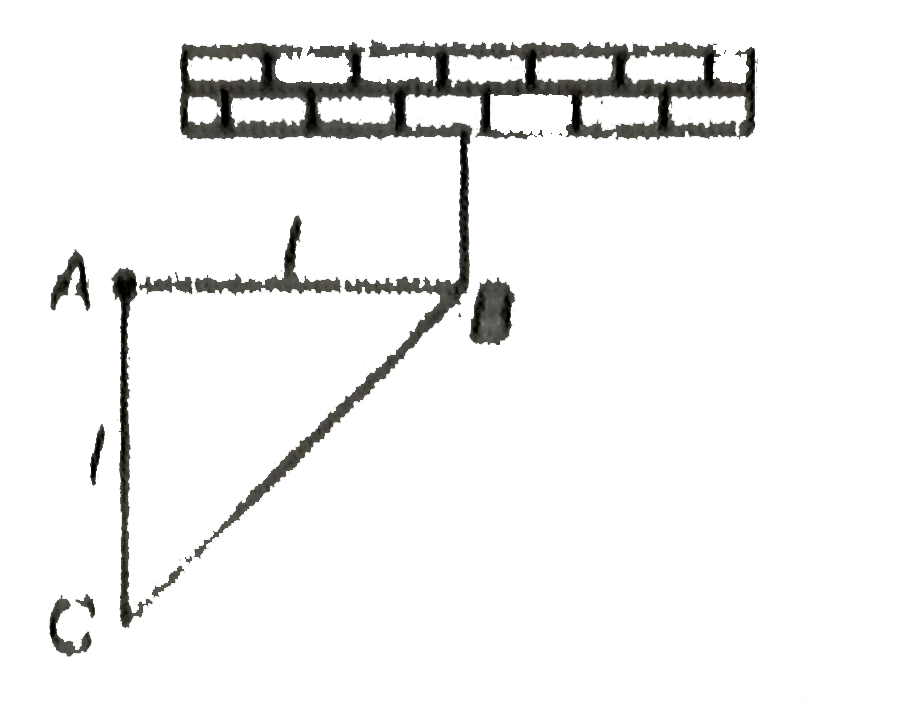 02:25View Solution
02:25View SolutionA uniform circular disc of radius `r` is placed on a rough horizontal surface and given a linear velocity `v_(0)` and angular velocity `omega_(0)` as shown. The disc comes to rest after moving some distance to the right. It follows that
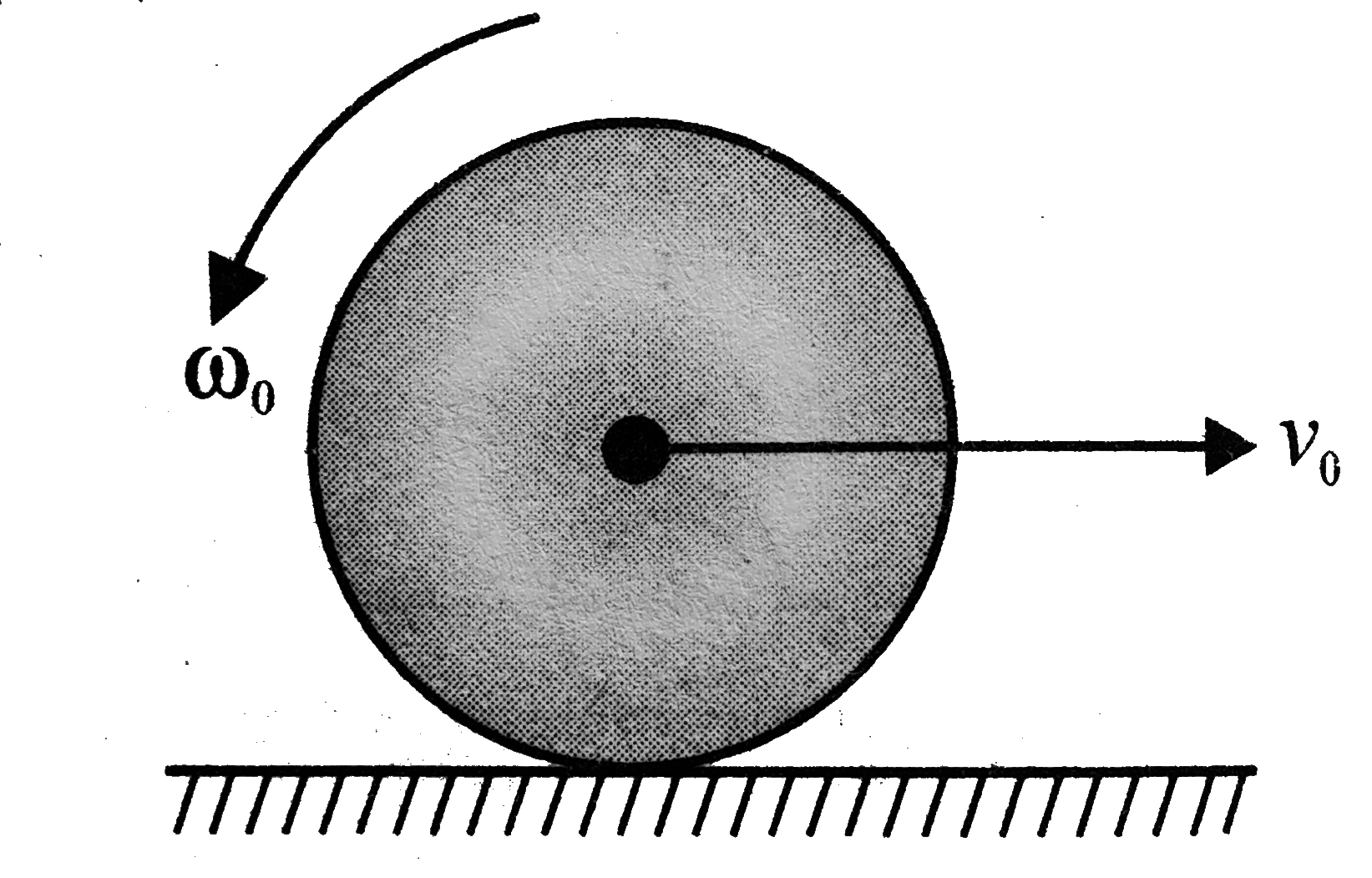 05:00View Solution
05:00View SolutionThe radius of gyration of a solid hemisphere of mass M and radius Rn about an axis parallel to the diameter at a distance `(3)/(4)`R is given by (centre of mass of the hemisphere lies at a height `3R//8` from the base.)
 06:29View Solution
06:29View SolutionTwo particles A and B are moving with constant velocities `V_(1)=hatj` and `v_(2)=2hati` respectively in XY plane. At time t=0, the particle A is at co-ordinates (0,0) and B is at (-4,0). The angular velocities of B with respect to A at t=2s is (all physical quantities are in SI units)
01:55View SolutionA uniform disc of radius `R` lies in the `x-y` plane, with its centre at origin. Its moment of inertia about z-axis is equal to its moment of inertia about line `y = x + c`. The value of `c` will be.
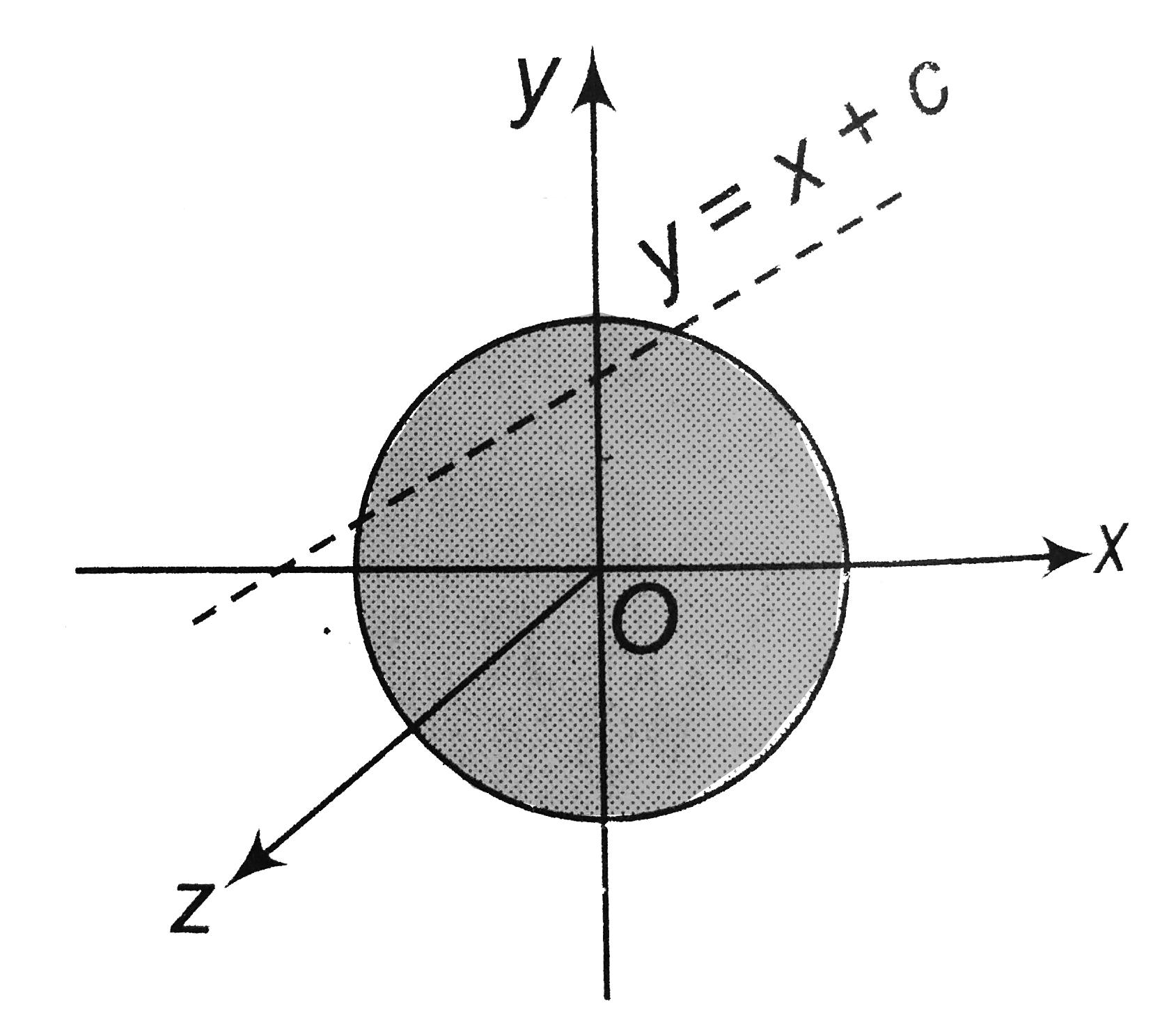 .06:51View Solution
.06:51View SolutionA uniform rod of mass m and lkength 2a lies at rest on rotating with angular speed `omega_(0)=40rad//s` is placed between two smooth walls on a rough ground. Distance between the walls is slightly greater than the diameter of the sphere . Cofficent of friction between the sphere and the ground is `mu`=0.1. Sphere will stop rotating after time t=.......s.
View SolutionA solid sphere of mass 5 kg and and radius 1 m after rotating with angular speed `omega_(0)=40 rad//s` is placed between two smooth walls on a rough ground. Distance between the walls is slightely greater than the diameter of the sphere. Coffiecient of friction between the sphere and the ground is `mu=0.1`. sphere will stop rtotating after time t = ...........s .
 03:49View Solution
03:49View SolutionA ring of mass m is rolling without slipping with linear velocity v as shown is figure. A rod of identical mass is fixed alone one of its diameter. The total kinetic energy of the system is
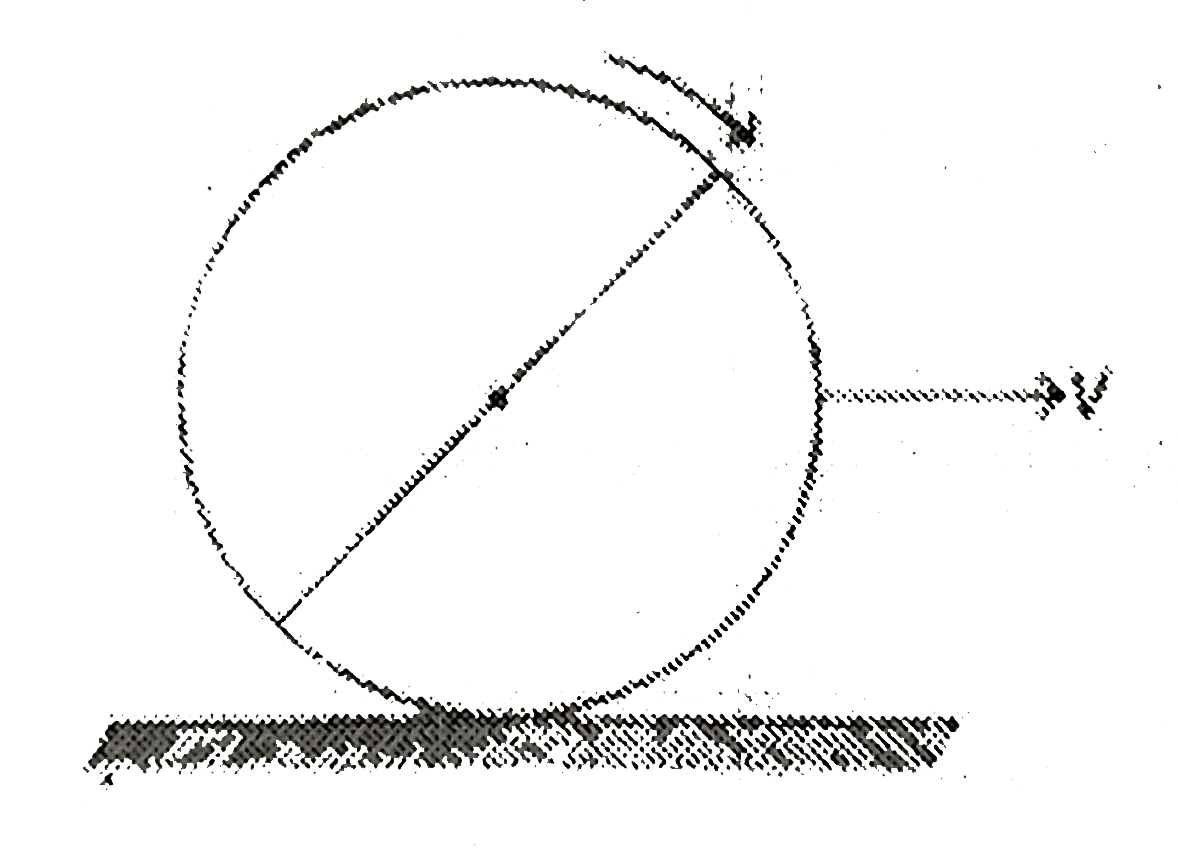 01:55View Solution
01:55View SolutionA cube of mass m and side a is moving along a plane with constant speed `v_(o)` as shown in figure. The magnitude of angular momentum of the cube about z -axis would be.
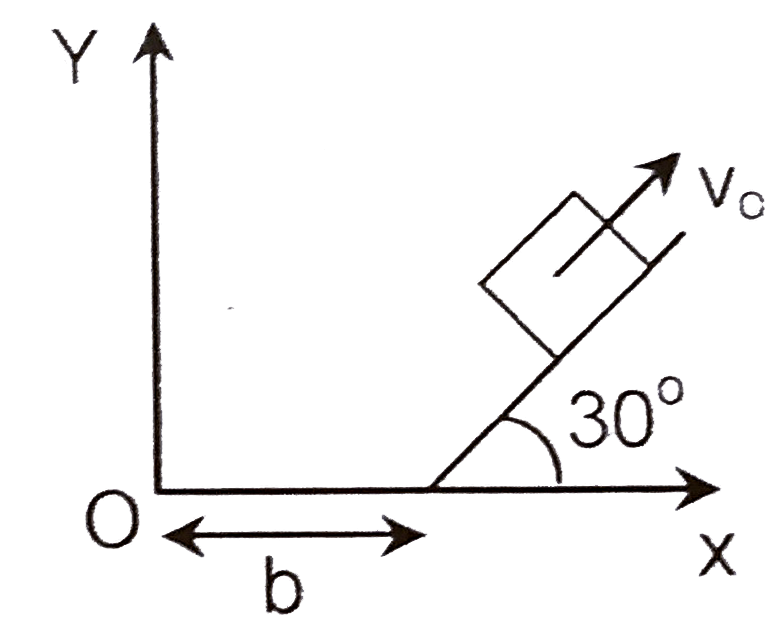 03:38View Solution
03:38View SolutionIn the pully system shown, if radii of the bigger and smaller pulley are 2m and 1m respectively and the acceleration of block A is `5 m//s^(2)` in the downward direction, then the acceleration of block B will be
 01:43View Solution
01:43View SolutionA uniform rod is hinged at its one end and is allowed to rotate in verticle plANE. Rod is given angular velocity `omega` in its verticle position as shown in figure. The value of `omega` for the force exerted by the hinge on rod is zero in this position is
 03:23View Solution
03:23View SolutionUniform rod Ab is hinged at the end A in the figure. The other end of the rod is connected toa block through a massless string as shown. The pulley is smooth and massless. Masses of the block and the rod are same and are equal to 'm'. Acceleration due to gravity is g. The tension in the thread and angular acceleration of the rod just after releases of block from this position are
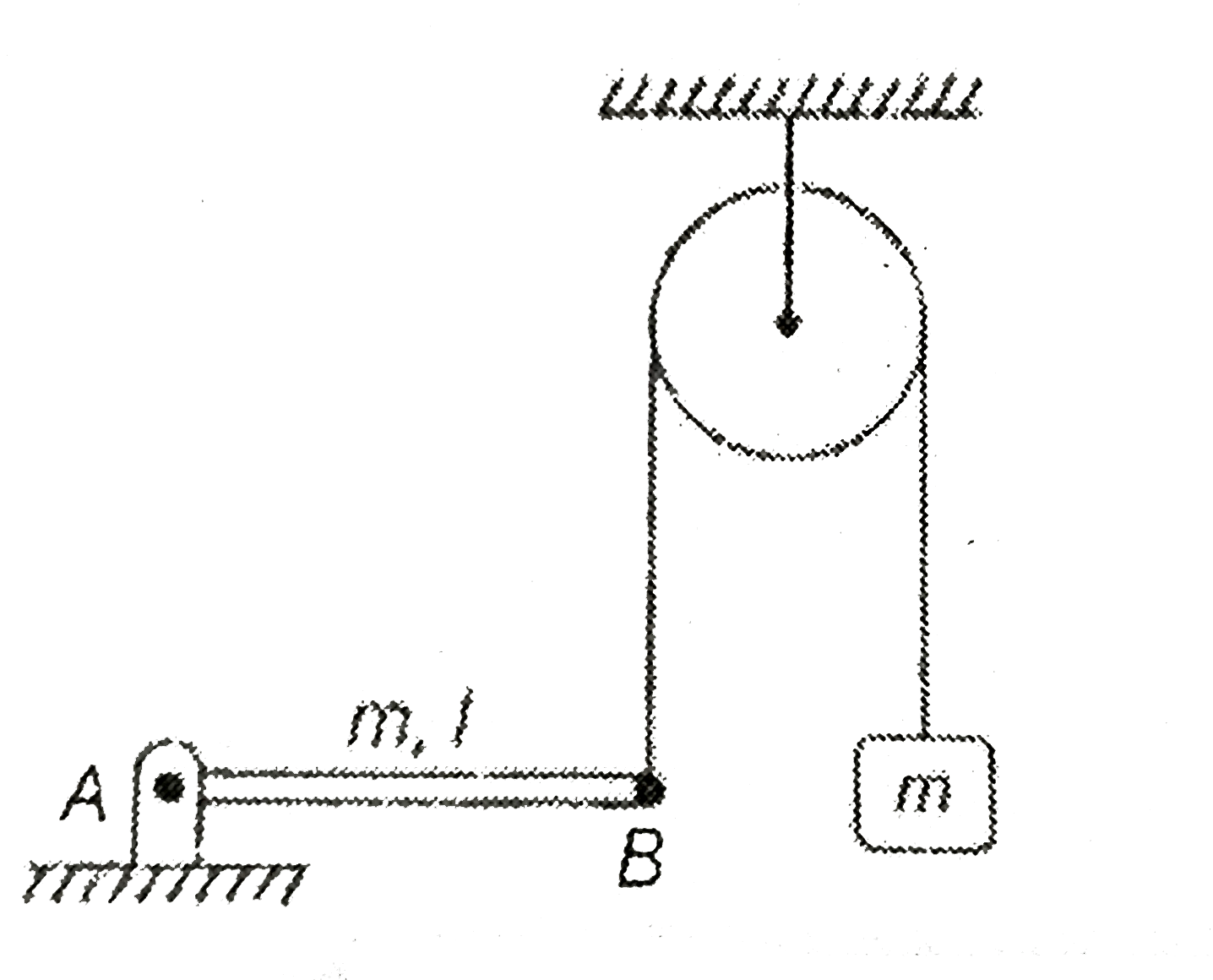 View Solution
View SolutionA uniform rod of mass m, length l is placed over a smooth horizontal surface along y -axis and is at rest as shown in figure. An impulsive force F is applied for a small time `Deltat` along x-direction at point A. The x-coordinte of end A of the rod when the rod becomes parallel to x-axis for the first is (in itially the coordinates opf centre of mass of the rod is (0,0).
 05:08View Solution
05:08View SolutionA uniform rectangular plate of mass m which is free to rotate about the smooth vwerticle hinge passing through the centre and perpendicular to the plate, is lying on a smooth horizontal surface. A particle of mass m is moving with speed 'u' collides with the plate and sticks to it as shown in figure. The angular velocity of the platye after colli9sion will be
 02:31View Solution
02:31View SolutionThe angular momentum of a particle about origin is varying as L =4t+8(SI units) whern its moves along a straight line y=x-4(x,y in metres). The magnitude of force acting on the particle will be
01:55View SolutionA Particle is attached to the lower end of a uniform rod which is hinged at its other end as shown in the figure. The minimum speed given to the particle so that the rod performs circular motion in a verticle plane will be [length of the rod is l, consider masses of bopth rod and particle to be same]
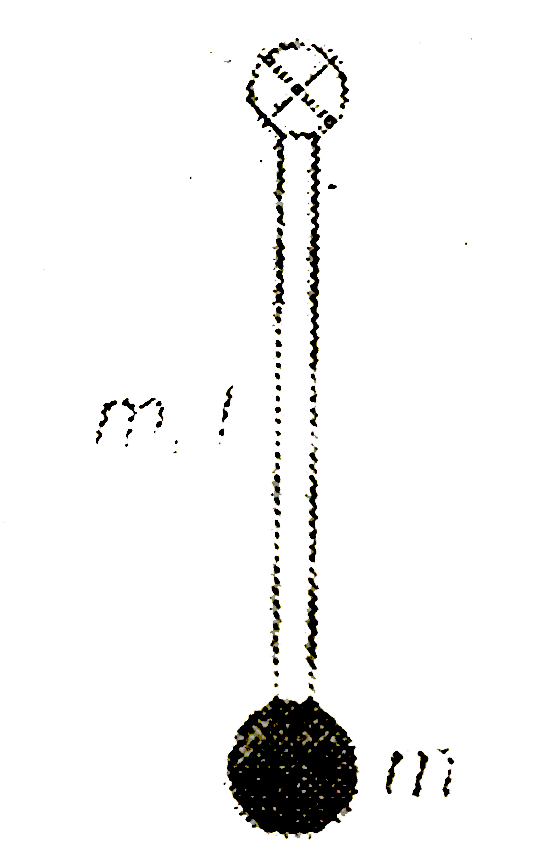 View Solution
View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with cofficent of friction `mu`. A horizontal force F is applied on the prism as shown in the figure. If the cofficent of the friction is sufficently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is
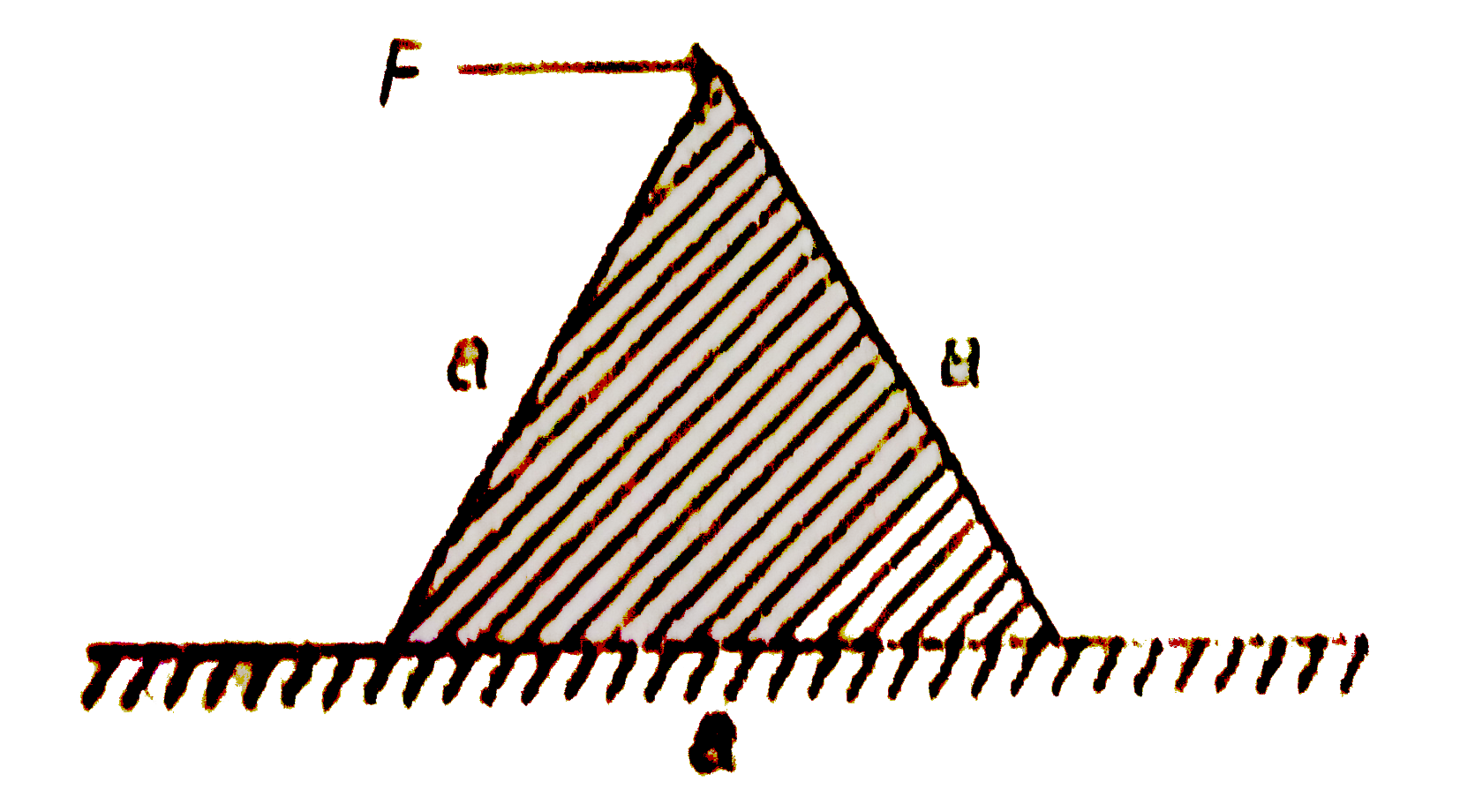 03:10View Solution
03:10View SolutionA sphere of mass m is given some angular velocity about a horizontal axis through its centre and gently placed on a plank of mass 'm'. The co-efficent of friction between the two is `mu`. The plank rests on a smooth horizontal surface. The initial acceleration of the centre of sphere relative to the plank will be
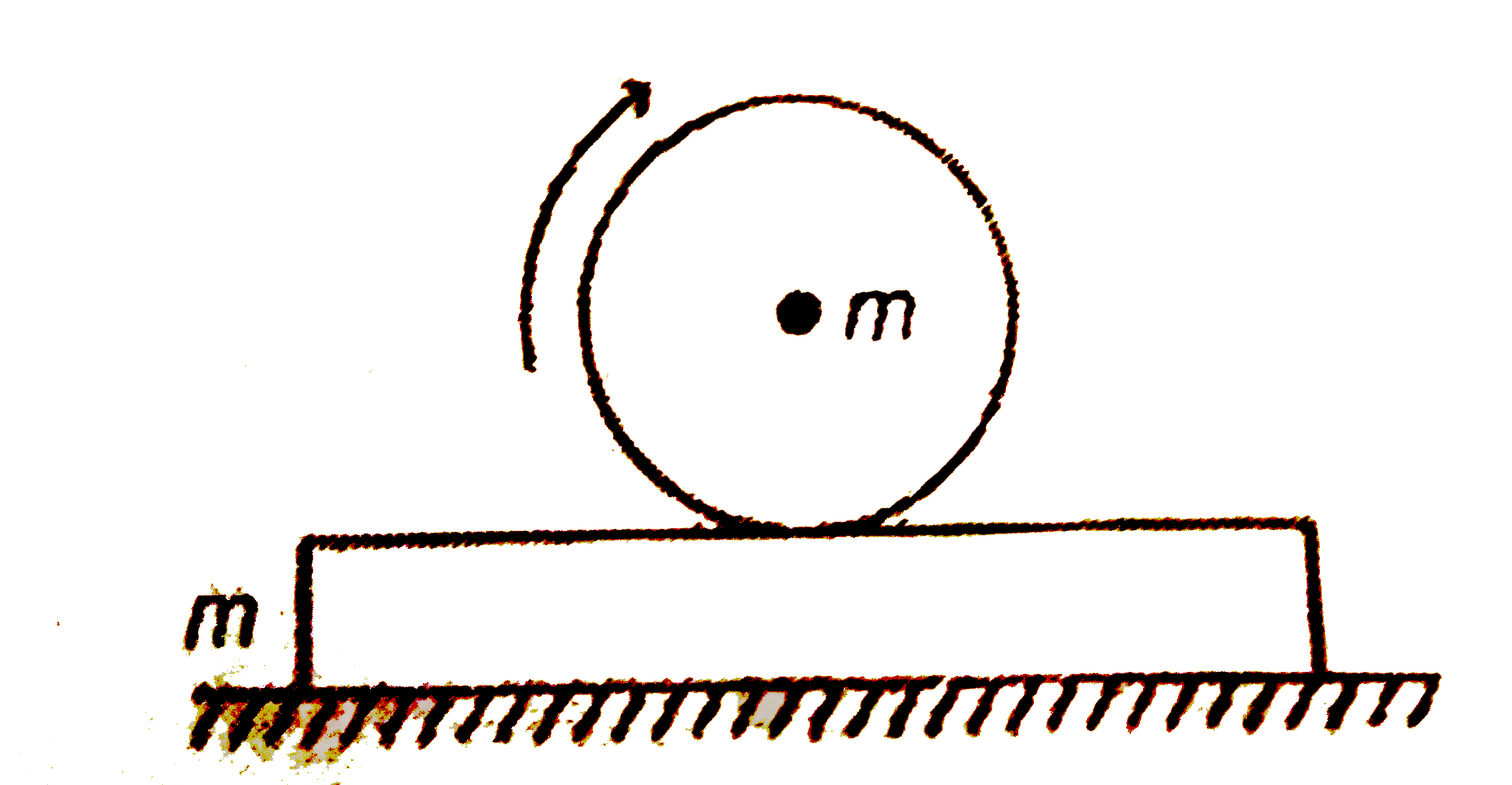 03:24View Solution
03:24View SolutionWhen a perosn throws a meter stivk it is found that the centre of the stick is moving with speed `10 m//s` and left end stick with speed `20 m//s`. Both points move vertically upwards at that moment. Then angular speed the stick is :
05:10View SolutionA rod of negligble mass and length l is pioveted at its centre. A particle of mass m is fixed to its left end and another particle of mass 2 m is fixed to the right end. If the system is released from rest and after sometime becomes vericle, The speed v of the two mases and angular velocity at that instant are
 08:20View Solution
08:20View SolutionA point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts
 View Solution
View SolutionA system of identical cylinders and plates is shown in Fig. All the cylinders are identical and there is no slipping at any contact. The velocity of lower and upper plates are `V` and `2V`, respectively, as shown in Fig. Then the ratio of angular speeds of the upper cylinders to lower cylinders is
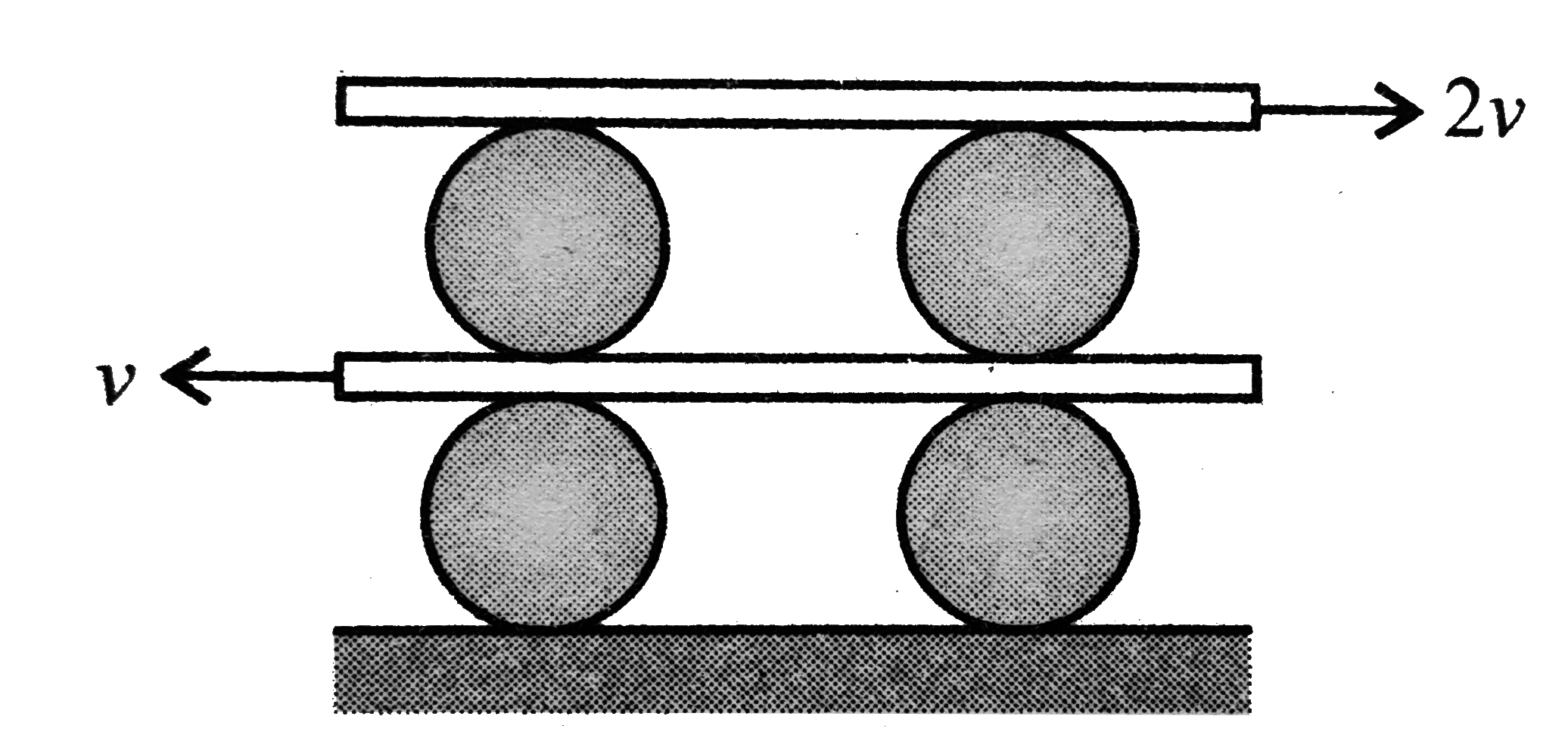 07:28View Solution
07:28View SolutionA box of dimensions l and b is kept on a truck moving with an acceleration a. if box does not slide, maximum acceleration for it to remain in equilibrium (w.r.t. truck) is
 07:54View Solution
07:54View SolutionInner and outer radii of a spool are r And R respectively. A thread is wound over ita ineer surface and placed over a rough horizontal surface. Thread is pulled by a force F as shown in the figure. Then in case of pure rolling.
 View Solution
View SolutionA disc of radius `R` is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity and acceleration vectors of point `P` is
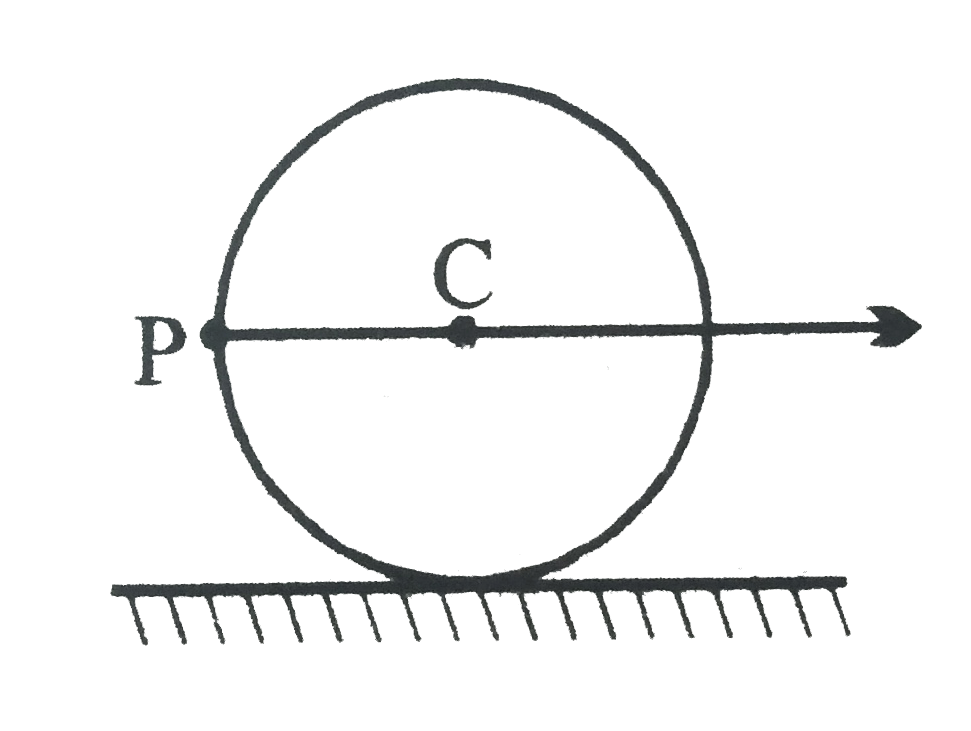 .02:05View Solution
.02:05View SolutionA uniform solid cylinder of mass 5kg and radius 0.1m is resting on a horizontal platform (parallel to the x-y plane) and is free to rotate about its axis along the y-axis the platform is given a motion in the x direction given by x=0.2 cos (10t) m if there is no slipping then maximum torque acting on the cylinder during its motion is
06:07View SolutionA rod lying on a frictionless horizontal surface is initially given an anglular velocity `omega` about vertical axis which passes through center of mass. The centre of mass is at rest but not fixed. The length of the rod is L. Subsequently, end A of the rod collides with nail P, which is near to A such that end A becomes stationery immediately after impact. Velocity of end B just after collision will be
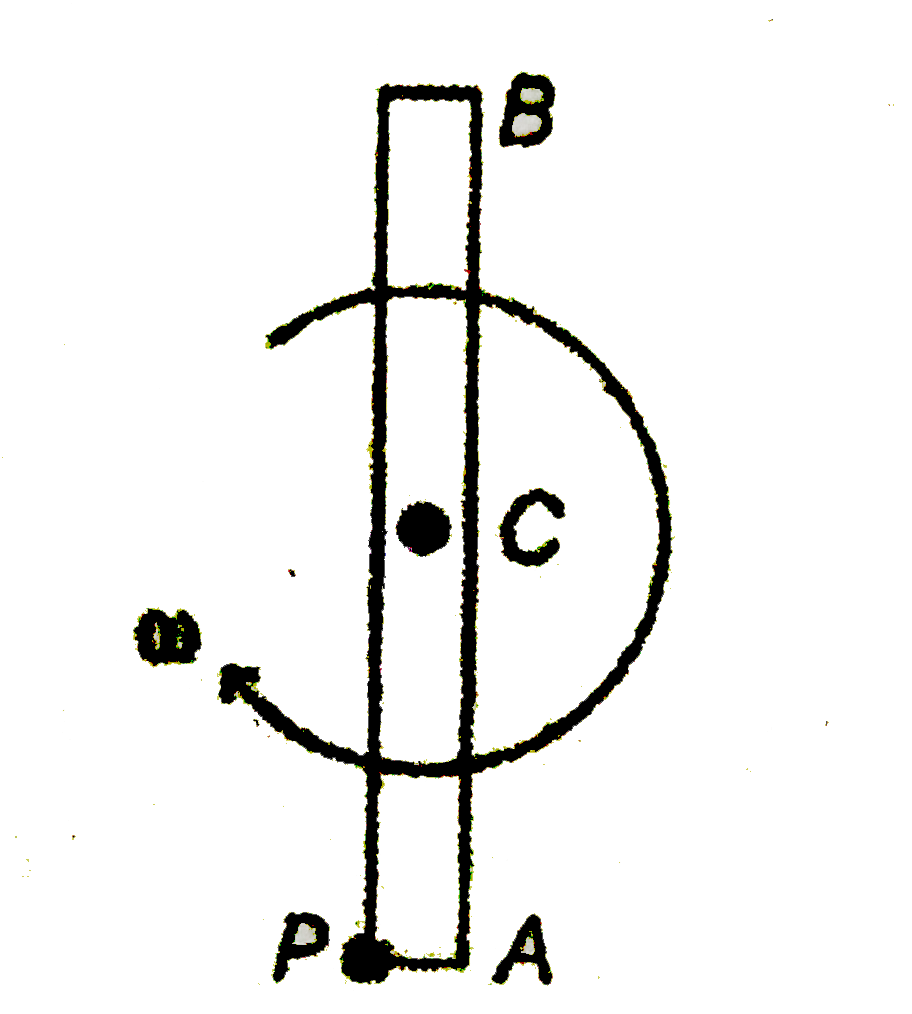 02:03View Solution
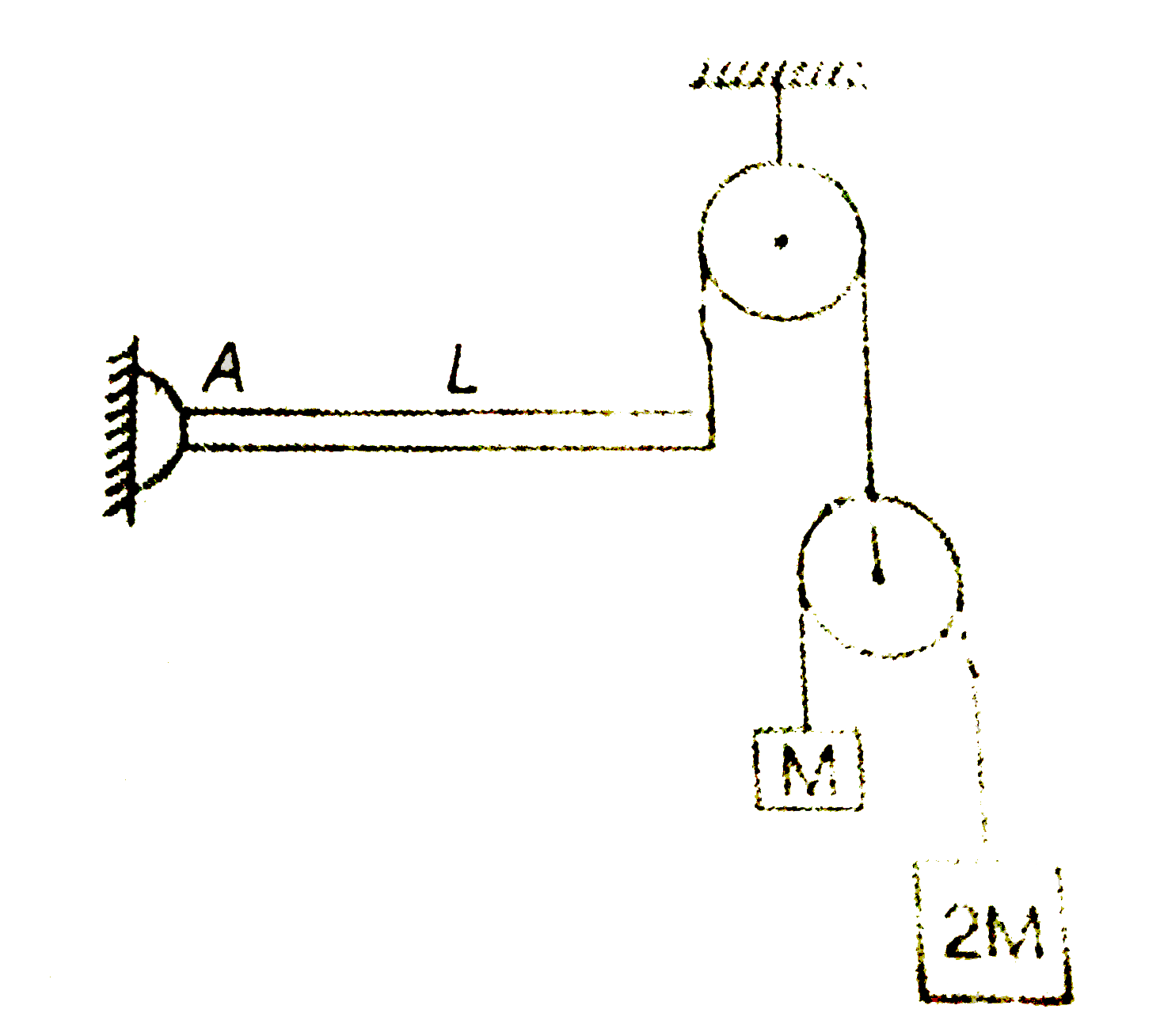
02:03View SolutionConsider the situation shown in the figure. Uniform rod of length L can rotat freely about the hinge A in vertical plane. Pulleys and stringa are light and frictionless. If the rod remains horizontal at rest when the system is released then the mass of the rod is
 View Solution
View SolutionA homogeneous rod of mass 3 kg is pushed along the smooth horizontal surface by a horizontal suface by a horizontal force F equal to 40 N. The angle `theta` for which rod hasd pure translation motion is `(g=10 m//s^(2))`
View SolutionA disc of mass M and radius R is placed on a rough horizontald surface. A light rod of length 2R is fixed to the disc at pointt A as shown in figure and force `(3)/(2)` Mg is applied at the other end of the rod. Find the minimum value of coefficient of friction (upto on decimal place ) between disc and horizontal surface, so that disc starts to roll without slipping .
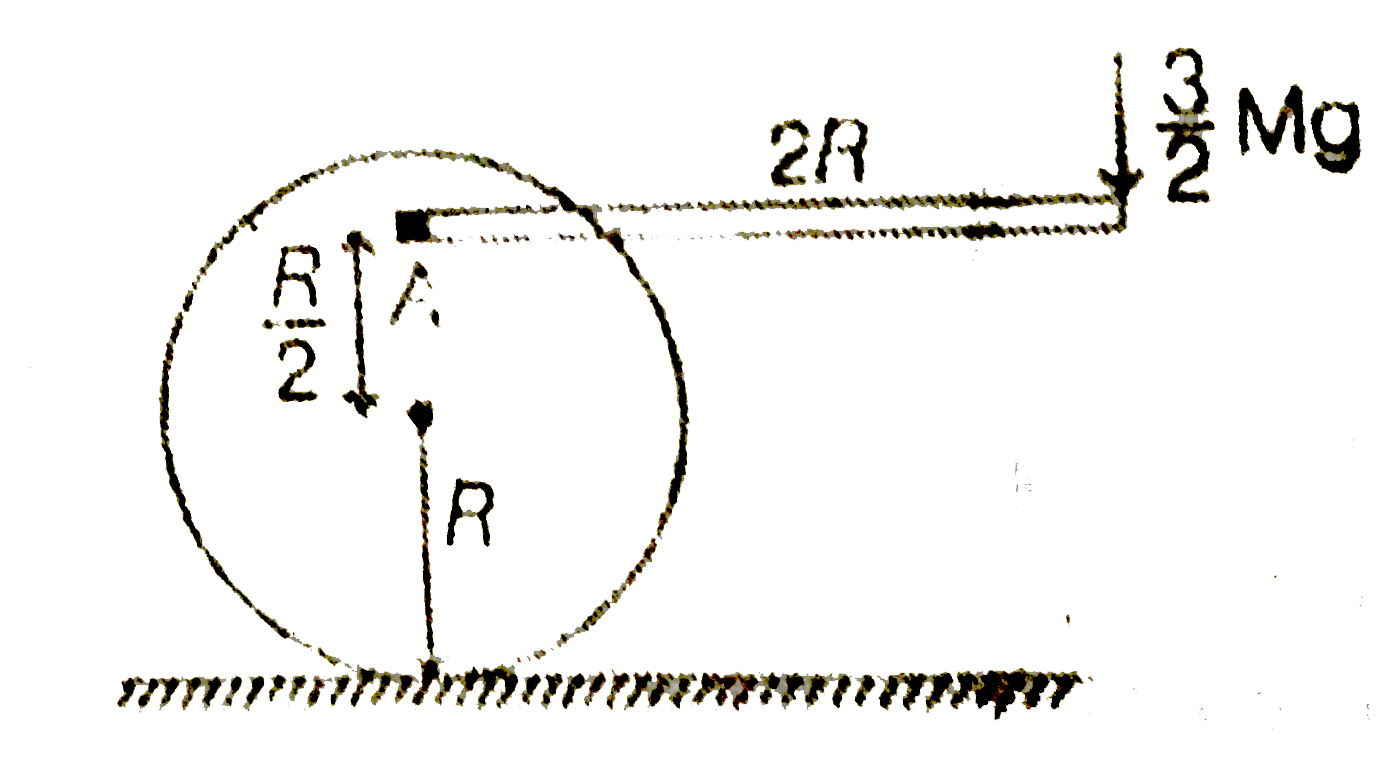 04:30View Solution
04:30View SolutionA uniform rod of mass m , length l moving with a velocity v ( perpendicular to its length ) on a smooth horizontal plane, encounters a fixed peg P at a distance l/4 from its nearer end. The rod collides with the peg. The duration of impact `Delta t` is very small. The average force exerted by the peg on the rod during the impact is of magnitude.
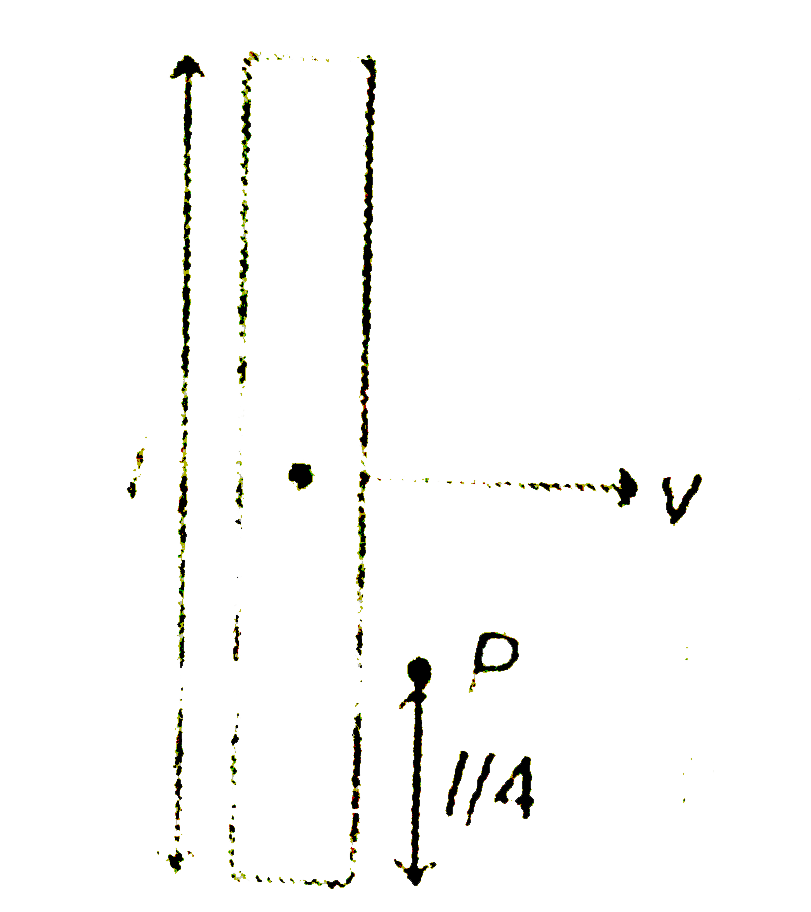 View Solution
View SolutionAn ideal inextensible string is wrapped over the disc of mass m and radius R. The other end of the string is connected to mass m. the string is passing over an ideal pulley A as shown in the figure. At any time t, mass m and disc are moving downward with acceleration of magnitude `a_(1) " and " a_(2)` respectively. The disc is rotating clockwise with angular acceleration of magnitude ` alpha` . There is no slipping betweeb string and disc. choose the incorrect option
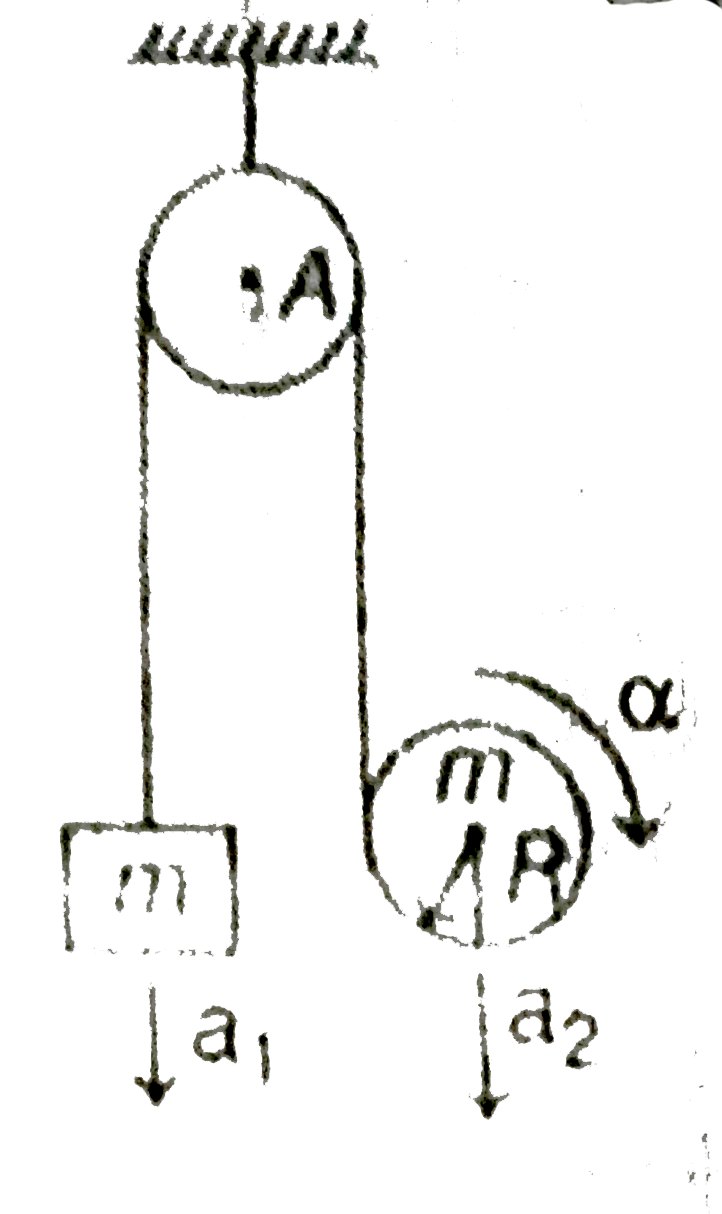 View Solution
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle `theta` with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed `V` in the horizontal plane then the angular momentum of the rod about the axis is:02:12View SolutionThe wheel of radius R rolls wihtout slipping on horizontal rough surface and its centre O has an acceleration `a_(0)` in forward direction. A point P on the wheel is a distance r from O and angular position ` theta` from horizontal. Find the angle ` theta` for which point P can have zero acceleration in this position .
 View Solution
View SolutionA string is warapped around a cylinder of mass m and radius r. The string is also connected to a block of same mass m with the help of another pulley as shown in figure. The angular acceleration of the cylinder is ( friction is sufficient for rolling ) ( all pulleys are ideal)
 View Solution
View SolutionA small uniform solid sphere A rolls down a fixed surface starting at a height h and collides elastically with a sphere B which is identical in size to A but has twice its mass. The speed of the sphere B, just after the collision is
 03:18View Solution
03:18View SolutionA small disc is released from rest at A on an inclined plane AB so that it rolls down wihtout slipping. It reaches the bottom with linear velocity `v_(1)` in time `t_(1)`. Next a small ring released form rest on the inclined plane AC so that it rolls down without slipping. It reaches the bottom with linear vlocity `v_(2)` in time `t_(2)`. Given `theta_(1)=30^(@), theta_(2)=60^(@),` and h=10m. Then,
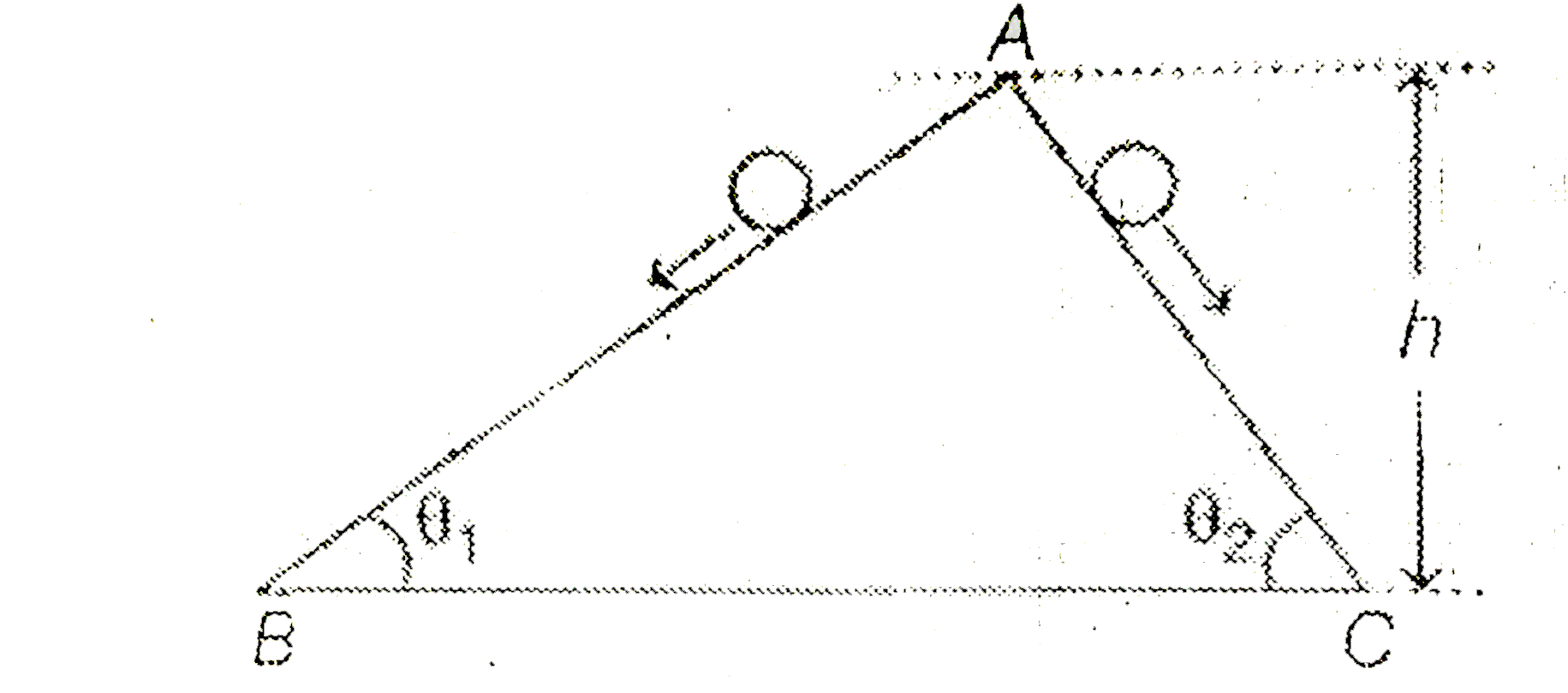 04:28View Solution
04:28View SolutionA solid ball is realeased from rest down inclines of various inclination angle `theta` but through a fixed vertical height h. The coefficient of static and kinetic friction are both equal to `mu`. Which of the following graph best represents the total kinetic energy K of the ball at the bottom of the incline as a function of the angle `theta` of the incline?
04:22View Solution
A Only One Option is Correct questions and complete solutions for chapter ROTATIONAL MOTION of DC PANDEY PHYSICS (HINGLISH) of Class 11
