Complete Solutions to Solved Examples of chapter FLUID MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FLUID MECHANICS |
| DC PANDEY | Solved Examples |
| Number Of Questions | 21 |
| Academic Year | 2023-24 |
A block of wood floats in a bucket of water placed in a lift. Will the block sink more or less if the lift starts accelerating up?
View SolutionA raft of wood (density`=600kg//m^(3))` of mass `120 kg` floats in water. How much weight can be put on the raft to make it just sink?
View SolutionA piece of ice is floating in a glass vessel filled with water. Then prove that level of water in the vessel remains unchanged after melting of ice.
View SolutionA piece of ice having a stone frozen in it floats in a glass vessel filled with water. How will the level of water in the vessel change when the ice melts?
View SolutionA solid floats in a liquid of different material. Carry out an analysis to see whether the level of liquid in the container will rise or fall when the solid melts.
View SolutionA metallic sphere weighs `210g` in air, 180 g in water and 120 g in an unknown liquid. Find the density of metal and of liquid.
View SolutionAn ornament weighing `50g` in air weighs only `46 g` in water. Assuming that some copper is mixed with gold to prepare the ornament, find the amount of copper in it. Specific gravity of gold is `20` and that of copper is `10`.
View SolutionAn iron casting containing a number of cavities weight `6000N` in air and `4000N` in water. What is the volume of the cavities in the casting? Density of iron is `7.87g//cm^(3)`. Take `g = 9.8 m//s^(2)` and density of water `= 10^(3) kg//m^(3)`.
View SolutionA liquid kept in a container has a horizontal acceleration 'a' as shown in figure.
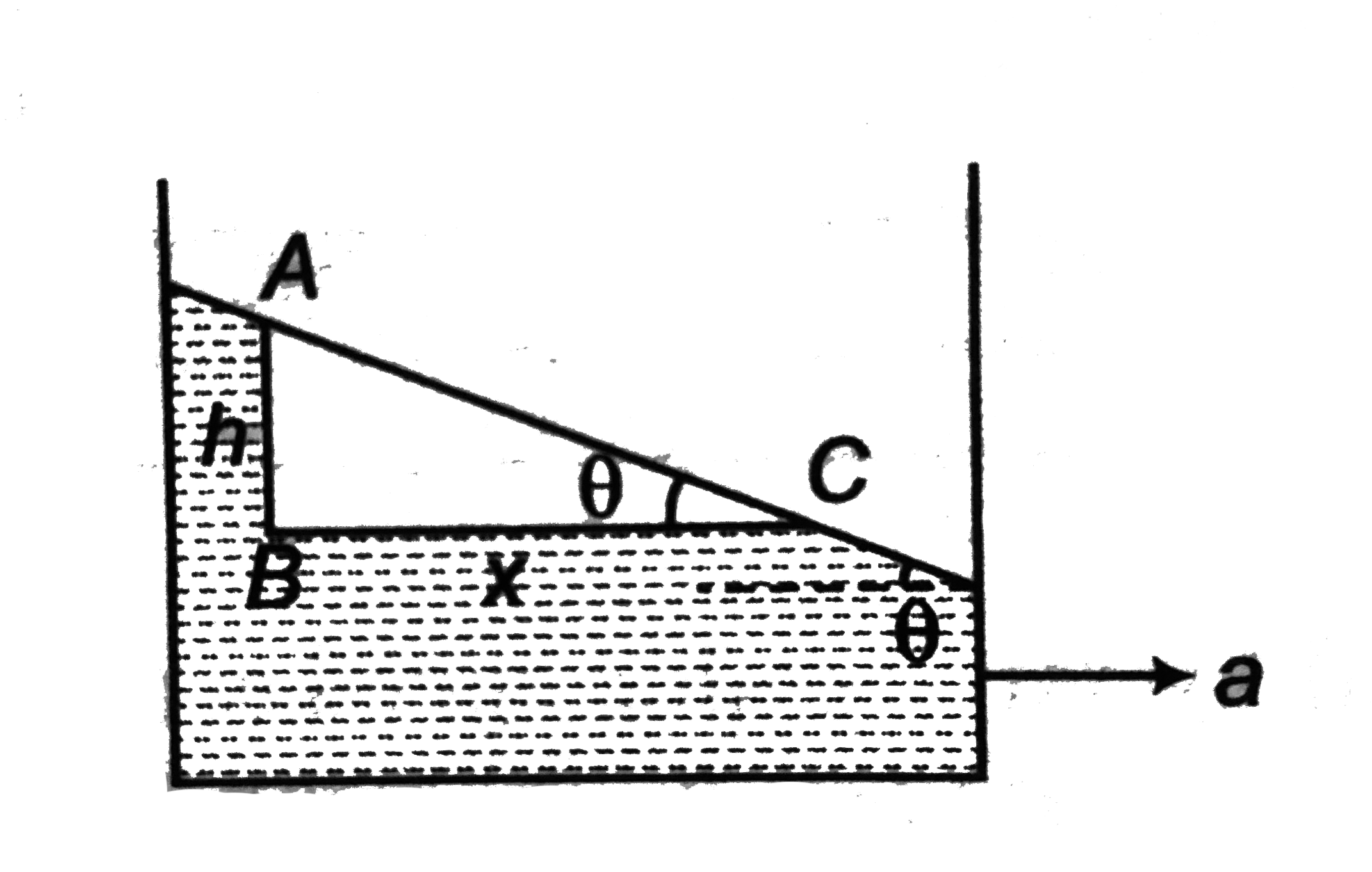
Using the pressure equation along the path ABC find the angle `theta`.
View SolutionA liquid of density `'rho'` is rotated with an angular speed `'omega'` as shown in figure. Using the pressure equation concept find the equation of free surface of the liquid.
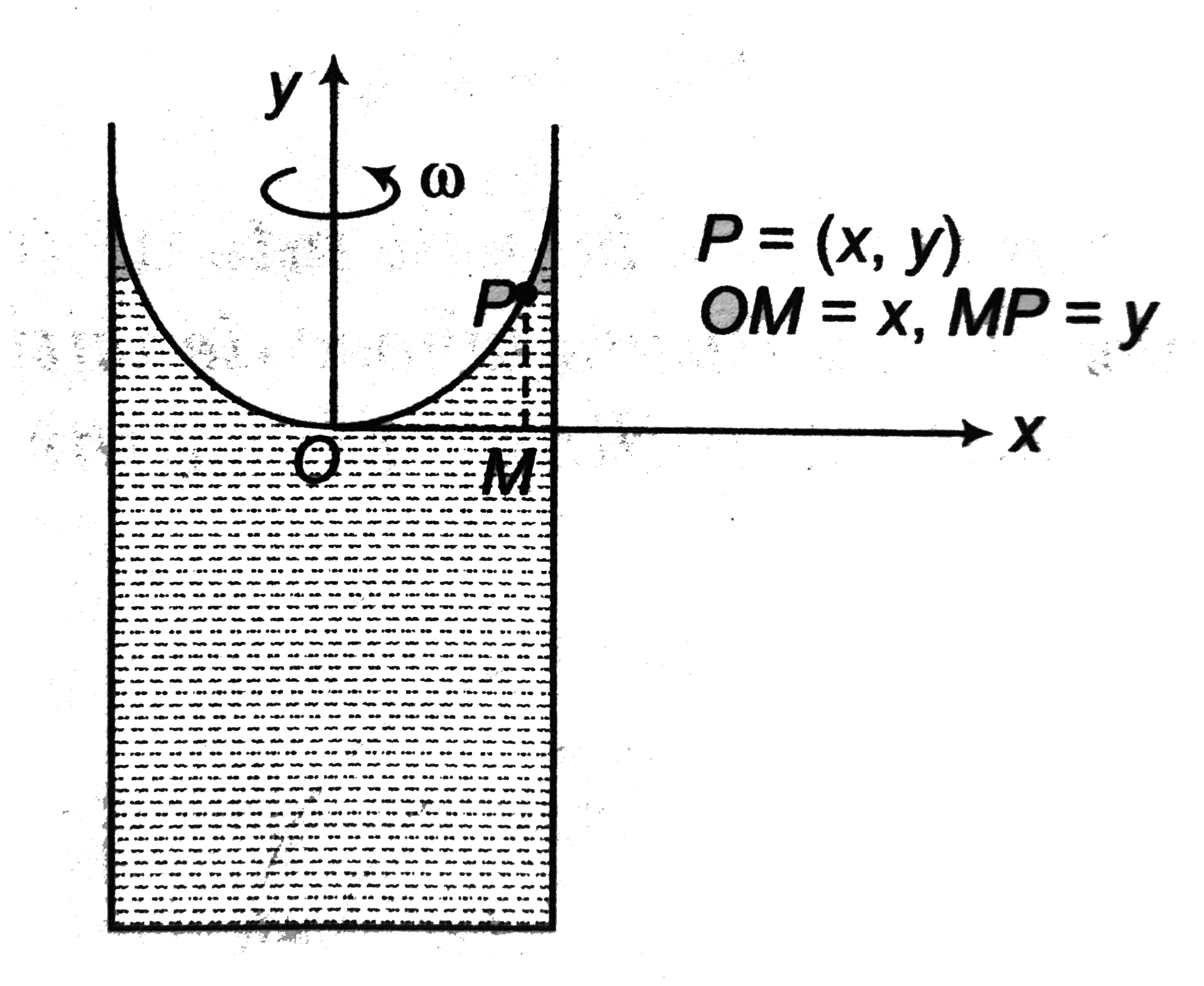 .
.
View Solution
A liquid of density `rho` is rotated by an angular speed `omega` as shown in figure, Using the concept of pressure equation, find a relation between `h_(1),h_(2),x_(1)` and `x_(2)`.
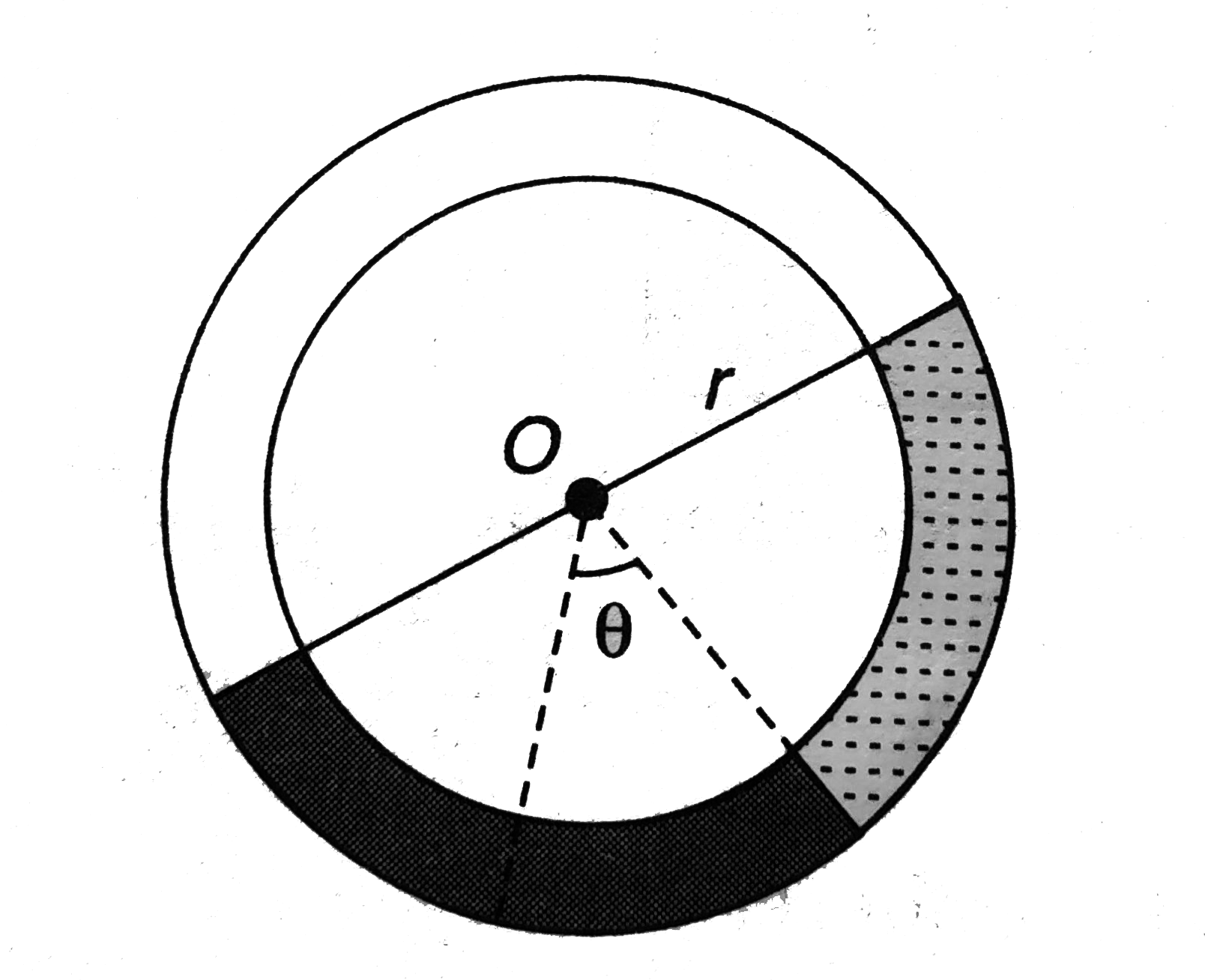
View SolutionA small uniform tube is bent into a circle of radius `r` whose plane is vertical. Equal volumes of two fluids whose densities are`rho` and `sigma(rhogtsigma)` fill half the circle. Find the angle that the radius passing through the interface makes with the vertical.
View SolutionThe U-tube acts as a water siphon. The bend in the tube is 1m above the water surface. The tube outlet is 7m below the water surface. The water issues from the bottom of the siphon as a free jet at atmospheric pressure. Determine the speed of the free jet and the minimum absolute pressure of the water in the bend. Given atmospheric pressure `=1.01xx 10^(5)N//m^(2),g=9.8 m//s^(2)` and density of water `=10^(3)kg//m^(3)`
 .
.
View SolutionA liquid of density `rho` is filled upto a geight of 'h' in a container as shown in firgure. Base of the contaimer is a square of side L. Ignoring the atmospheric pressure find

(a) pressure force `F_(1)` on its base.
(b) torque of force `F_(1)` about an axis passing through `C` and perpendicular to plane of paper.
(c) Pressure force `F_(2)` on the vertical side wall DC.
(d) torque of force `F_(2)` about the same axis mentioned in part (b).
(e) point of application of force `F_(2)`
View SolutionA uniform solid cylinder of density `0.8g//cm^3` floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical.
The densities of the liquids A and B are `0.7g//cm^3` and `1.2g//cm^3`, respectively. The height of liquid A is `h_A=1.2cm.` The length of the part of the cylinder immersed in liquid B is `h_B=0.8cm`.

(a) Find the total force exerted by liquid A on the cylinder.
(b) Find h, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.
View SolutionWater is filled up to a height h in a beaker of radius `R` as shown in the figure. The density of water is `rho`, the surface tension of water is `T` and the atmospheric presure is `p_(0)`. Consider a vertical section `ABCD `of the water on one side of this section by water on the other side of this section has magnitude

(a) `|2p_(0)Rh+pi R^(2)rho gh-2 RT|`
(b)`|2p_(0)Rh+R rho gh^(2)=2RT|`
(c ) `|p_(0)(pi) R^(2)+R rho gh^(2)-2RT|`
(d) `|p_(0)pi R^(2)+R rho gh^(2)+2RT|`.
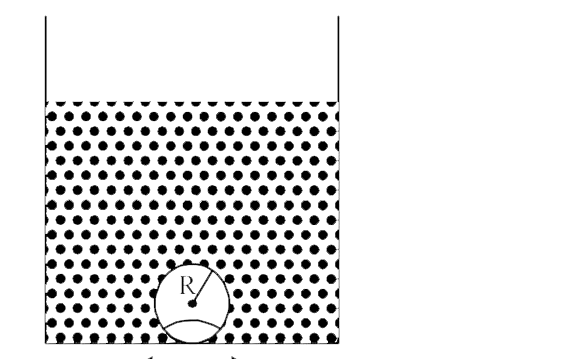
View SolutionOn heating water, bubbles being formed at the bottom of the vessel detach and rise. Take the bubbles to be spheres of radius R and making a circular contact of radius r with the bottom of the vessel. If `rlt ltR` and the surface tension of water is T, value of r just before bubbles detach is: (density of water is `rho_w`)
View SolutionWhen liquid medicine of density `rho` is to be put in the eye, it is done with the help of a dropper. As the bylb on the top of the dropper is pressed. A drop frons at the opening of the dropper. We wish to estimate the size of the drop.
We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy, To determine the size. We calculate the net vertical force due to the surface tension T when the radius of the drop is R. when this force become smaller than the weight of the drop the drop gets detached from the dropper.
If the radius of the opening of the dropper is r, the vertical force due to the surface tension on the drop of radius`R`(assuming `rlt ltR)` is
View SolutionWhen liquid medicine of density `rho` is to be put in the eye, it is done with the help of a dropper. As the bylb on the top of the dropper is pressed. A drop frons at the opening of the dropper. We wish to estimate the size of the drop.
We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy, To determine the size. We calculate the net vertical force due to the surface tension T when the radius of the drop is R. when this force become smaller than the weight of the drop the drop gets detached from the dropper.
If `r=5xx10^(-4)m,rho=10^(3) kg m^(-3), g=10ms^(-2), T=0.11Nm^(-1),` The radius of the drop when it detaches from the dropper is approximately,
View SolutionWhen liquid medicine of density `rho` is to be put in the eye, it is done with the help of a dropper. As the bulb on the top of the dropper is pressed, a drop forms at the opening of the dropper. We wish to estimate the size of the drop.
We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy, To determine the size. We calculate the net vertical force due to the surface tension `T=0.11Nm` when the radius of the drop is `R=1.4mm`. When this force become smaller than the weight of the drop, the drop gets detached from the dropper.
After the drop detaches, its surface energy is
View SolutionA drop of water of volume `0.05 cm^(3)` is pressed between two glass plates, as a consequence of which, it spreads and occupies an area of `40 cm^(2)`. If the surface tension of water is `70 "dyne"//cm`, find the normal force required to separate out the two glass plates in newton.
View Solution
Solved Examples questions and complete solutions for chapter FLUID MECHANICS of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS FLUID MECHANICS
- Assertion and Reason
- B) Medical entrance special format question
- Check point 13.1
- Check point 13.2
- Check point 13.3
- Check point 13.4
- Example
- Example 13.1
- Example 13.10
- Example 13.11
- Example 13.12
- Example 13.13
- Example 13.14
- Example 13.15
- Example 13.16
- Example 13.17
- Example 13.18
- Example 13.19
- Example 13.2
- Example 13.20
- Example 13.21
- Example 13.22
- Example 13.23
- Example 13.24
- Example 13.25
- Example 13.26
- Example 13.27
- Example 13.28
- Example 13.29
- Example 13.3
- Example 13.30
- Example 13.31
- Example 13.32
- Example 13.33
- Example 13.34
- Example 13.35
- Example 13.4
- Example 13.5
- Example 13.6
- Example 13.7
- Example 13.8
- Example 13.9
- Exercise16.1
- Exercise16.2
- Exercise16.3
- Exercise16.4
- Exercise16.5
- Exercise16.6
- Exercise16.7
- Exercise16.8
- Introductory Exercise
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 Comprehension Based
- Level 2 More Than One Correct
- Level 2 Single Correct
- Match the columns
- Medical entranes gallery
- Miscellaneous Examples
- Solved Examples
- Subjective
- Subjective Question
- Taking it together