
A liquid of density ρ is rotated by an angular speed ω as shown in figure, Using the concept of pressure equation, find a relation between h1,h2,x1 and x2.
Writing pressure equation between points A and B, we have
pA+ρgh1−ρω2x212+ρω2x222−ρgh2=pB
Points A and B are open to atmosphere.
Therefore,
pA=pB=p0= atmospheric pressure.
Substituting the values in above equation we have,
ρgh1−ρω2x212+ρω2x222−ρgh2=0
On simplifying we get,
(h2−h1)=ω22g(x22−x21)
This is the desired relation between h1,h2,x1 and x2.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Miscellaneous Examples10videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Exercise16.16videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery49videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A uniform rod of length l is rotating with constant angular speed ω as shown in figure. Choose the graph which correctly shows the variation of T with x.
_2019_CBT7_E01_017_Q01.png) A
A_2019_CBT7_E01_017_O01.png) B
B_2019_CBT7_E01_017_O02.png) C
C_2019_CBT7_E01_017_O03.png) D
D_2019_CBT7_E01_017_O04.png)
- Question 2 - Select One

A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B isAhρgBlρaChρg−lρaDhρg+lρa - Question 3 - Select One

A jar filled with two non-mixing liquid 1 and 2 having densities ρ1 and ρ2 respectively. A solid ball, made of a material of density ρ3 is dropped in the jar. It come to equilibrium in the position shown in the figure. Which of the following is true for ρ1,ρ2 and ρ3?Aρ1<ρ<ρ3Bρ1<ρ3<ρ2Cρ3<ρ1<ρ2Dρ1<ρ3<ρ2
A liquid of density ρ is in a vessel rotating with angular velocity ω as shown in figure. If P0 is the atmospheric pressure, find pressure at a radial distance r from the axis.
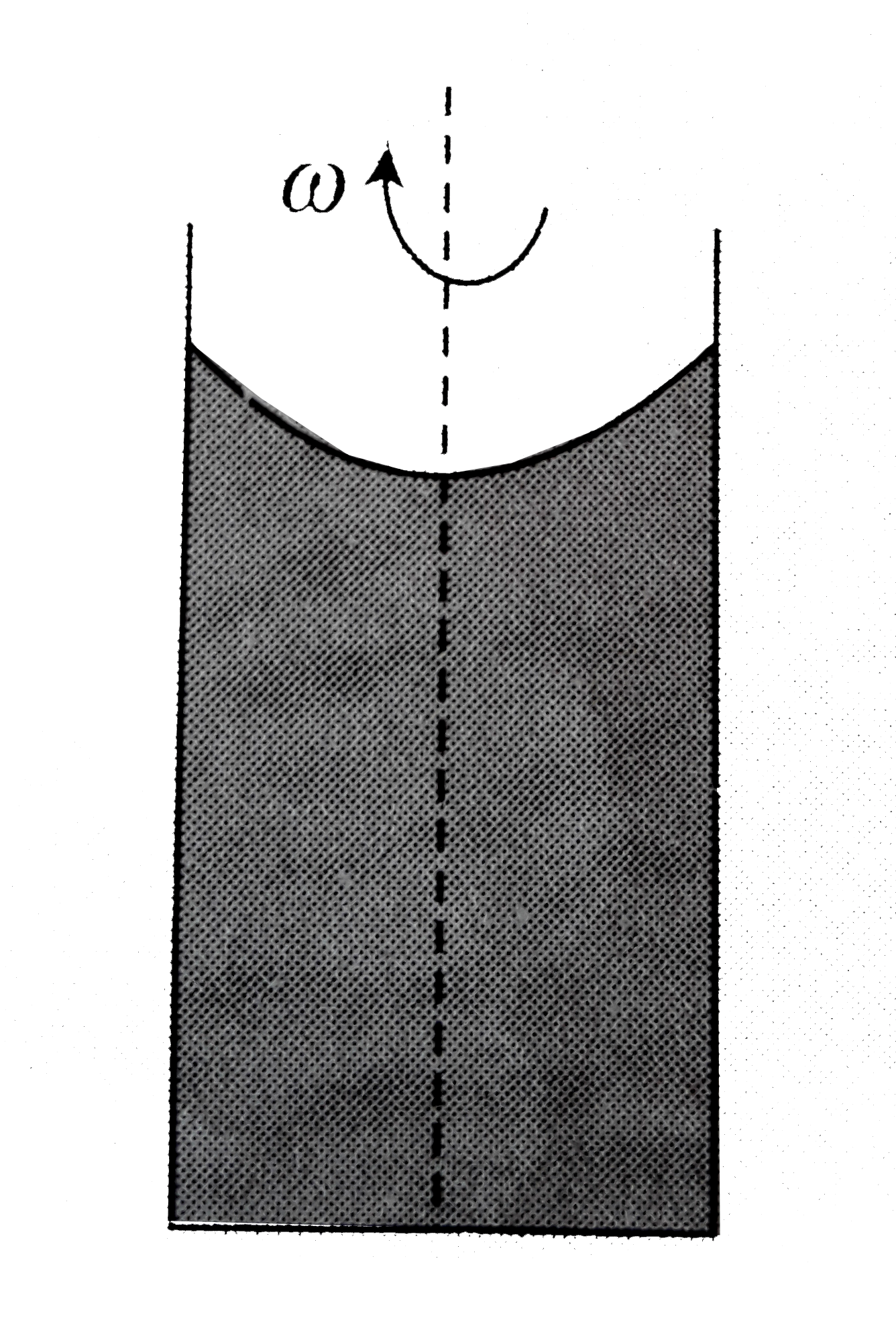 .View Solution
.View SolutionA liquid of density ρ is in a bucket that spins with angular velocity 'ω' as shown in figure. Prove that the free surface of the liquid has a parabolic shape. Find equation of this.
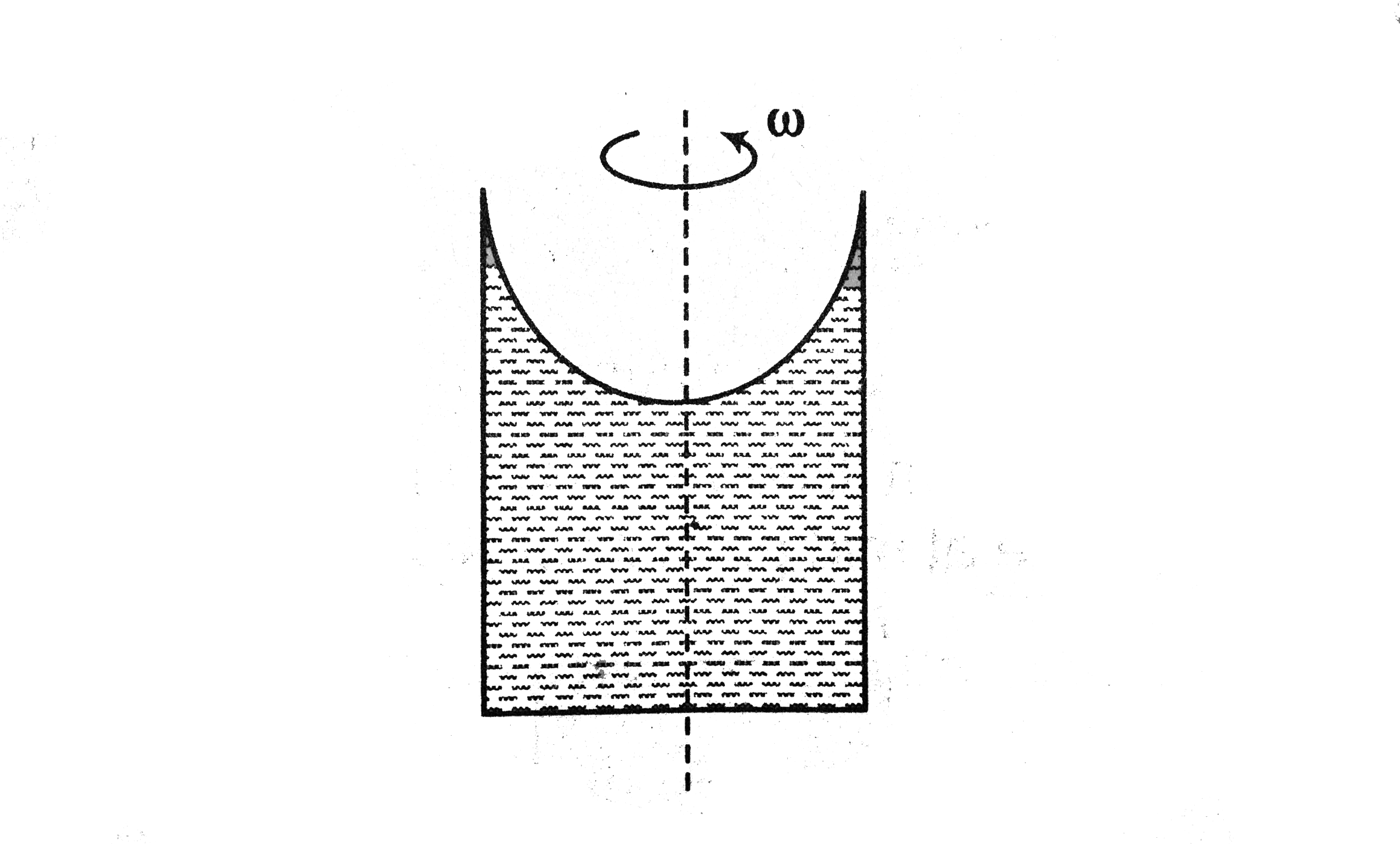 .View Solution
.View SolutionA vertical U-tube has a liquid up to a height h. If the tube is slowly rotated to an angular speed ω=√gh find the (i) heights of the liquid column, ii pressures at the points 1,2 and 3 in the limbs in steady state.
 View Solution
View SolutionEqual volumes of two immiscible liquids of densities ρand2ρ are filled in a vessel as shown in figure. Two small holes are punched at depth h/2 and 3h/2 from the surface of lighter liquid. If v1andv2 are the velocities of efflux at these two holes then (v2v1)2 is
 View Solution
View Solution
Using the concept of instantaneous axis of rotation. Find speed of particle P as shown in figure, under pure rolling condition.View Solution


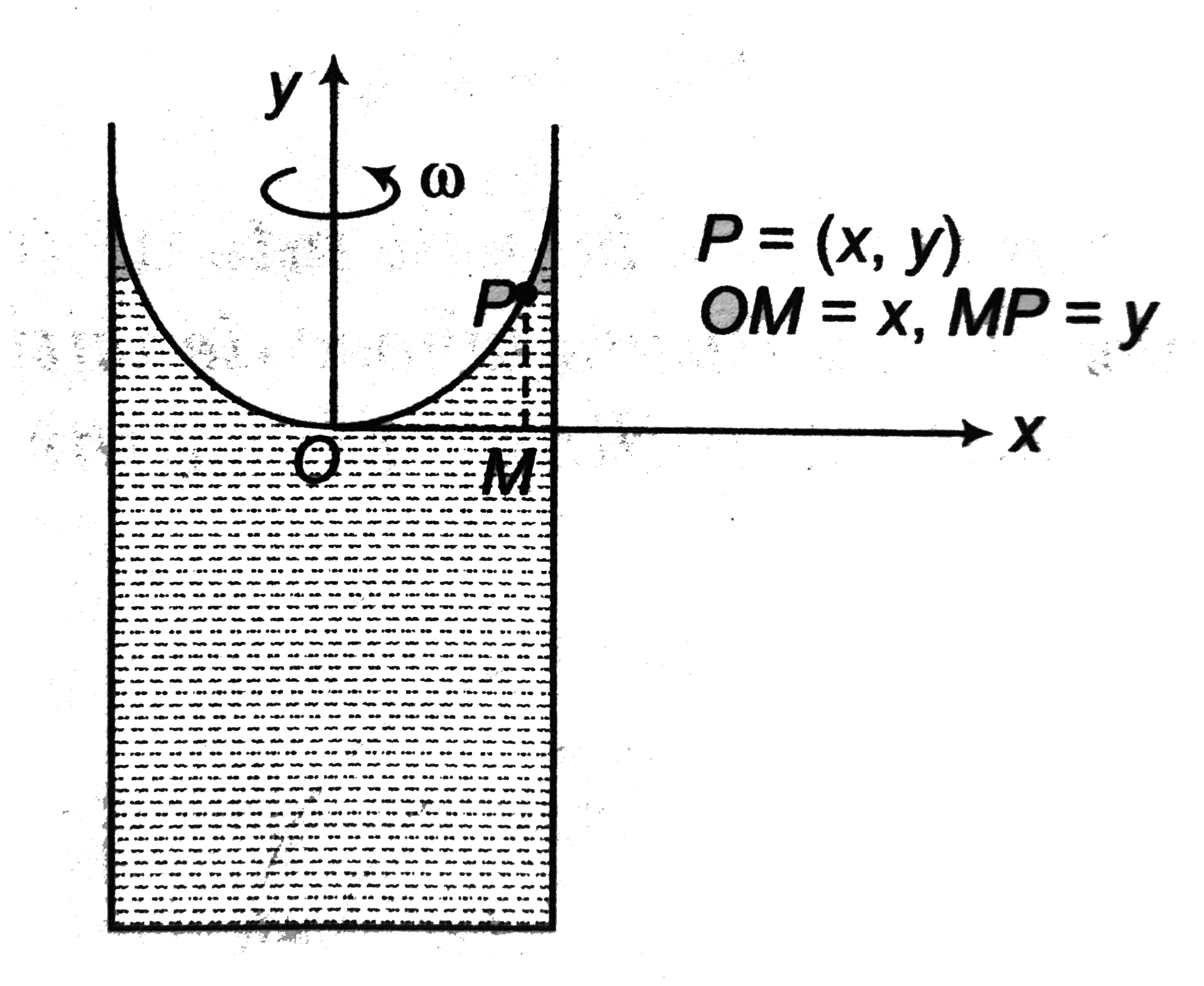 .
.