Complete Solutions to Taking it together of chapter CALORIMETRY AND HEAT TRANSFER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CALORIMETRY AND HEAT TRANSFER |
| DC PANDEY NEET | Taking it together |
| Number Of Questions | 47 |
| Academic Year | 2023-24 |
The temperature of a body in increased from `27^(@)C` to `127^(@)C`. By what factor would the radiation emitted by it increase?
View SolutionThe calories of heat developed in 200 W heater in 7 min is estimated
View SolutionThe thickness of a metallic plate is 0.4 cm. The temperature between its two surfaces is `20^(@)C`. The quantity of heat flowing per second is 50 calories from `5cm^(2)` area. In CGS system, the coefficient of thermal conductivity will be
View SolutionA spherical black body with radius 12 cm radiates 640 w power at 500 K. If the radius is halved and the temperature doubled, the power radiated in watts would be
View SolutionRate of heat flow through a cylindrical rod is `H_(1)`. Temperatures of ends of rod are `T_(1)` and `T_(2)`. If all the dimensions of rod become double and temperature difference remains same and rate of heat flow becomes `H_(2)`. Then `(H_(1))/(H_(2))` is `0.x`. Find value of x.
View SolutionA sphere, a cube and a thin circular plate are heated to the same temperature. All are made of the same material and have the equal masses. Tf `t_(1),t_(2) and t_(3)` are the repective time taken by the sphere, cube and the circular plate in cooling down to common temperature, then
View SolutionCertain amount of heat is given to 100 g of copper to increase its temperature by `21^@C`. If same amount of heat is given to 50 g of water, then the rise in its temperature is (specific heat capacity of copper ` = 400 J kg^(-1) K^(-1)` and that for water ` = 4200 J kg^(-1) K^(-1))`
View Solution2gm of steam condenses when passed through 40 gm of water initially at `25^(@)C` . The condensation of steam raises the temperature of water to `54.3^(@)C` . What is the latent heat of steam
View SolutionTwo identical square rods of metal are welded end to end as shown in figure (i), 20 calories of heat flows through it in 4 minutes. If the rods are welded as shown in figure (ii), the same amount of heat will flow through the rods in
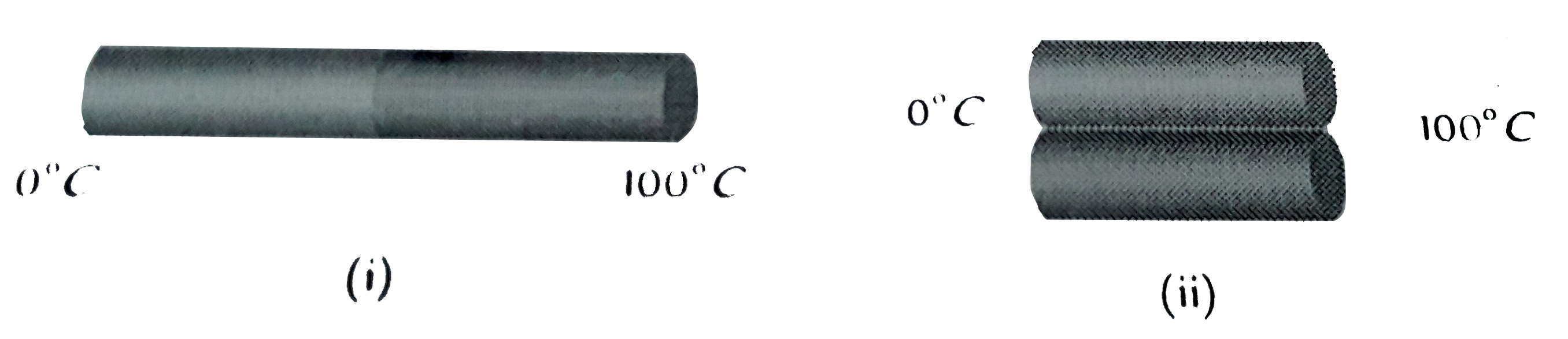
View SolutionThree rods of same dimensions have thermal condutivity `3K,2K` and `K` They are arranged as shown in Then the temperature of the junction in steady state is
 .
.
View SolutionA wall has two layers A and B each made of different materials. The layer A is 10cm thick and B is 20 cm thick. The thermal conductivity of A is thrice that of B. Under thermal equilibrium temperature difference across the wall is `35^@C`. The difference of temperature across the layer A is
View SolutionA body cools from `50^(@)C` to `40^(@)C` in 5 min. The surroundings temperature is `20^(@)C`. In what further times (in minutes) will it cool to `30^(@)C` ?
View SolutionA block of ice at `-10^@C` is slowly heated and converted to steam at `100^@C.` Which of the following curves represents the phenomenon qualitatively?
View SolutionIf one kilogram water at `100^(@)C` is vapourised in open atmosphere. The correct statement is
View SolutionA liquid cools from `50^(@)C` to `45^(@)C` in 5 minutes and from `45^(@)C` to `41.5^(@)C` in the next 5 minutes. The temperature of the surrounding is
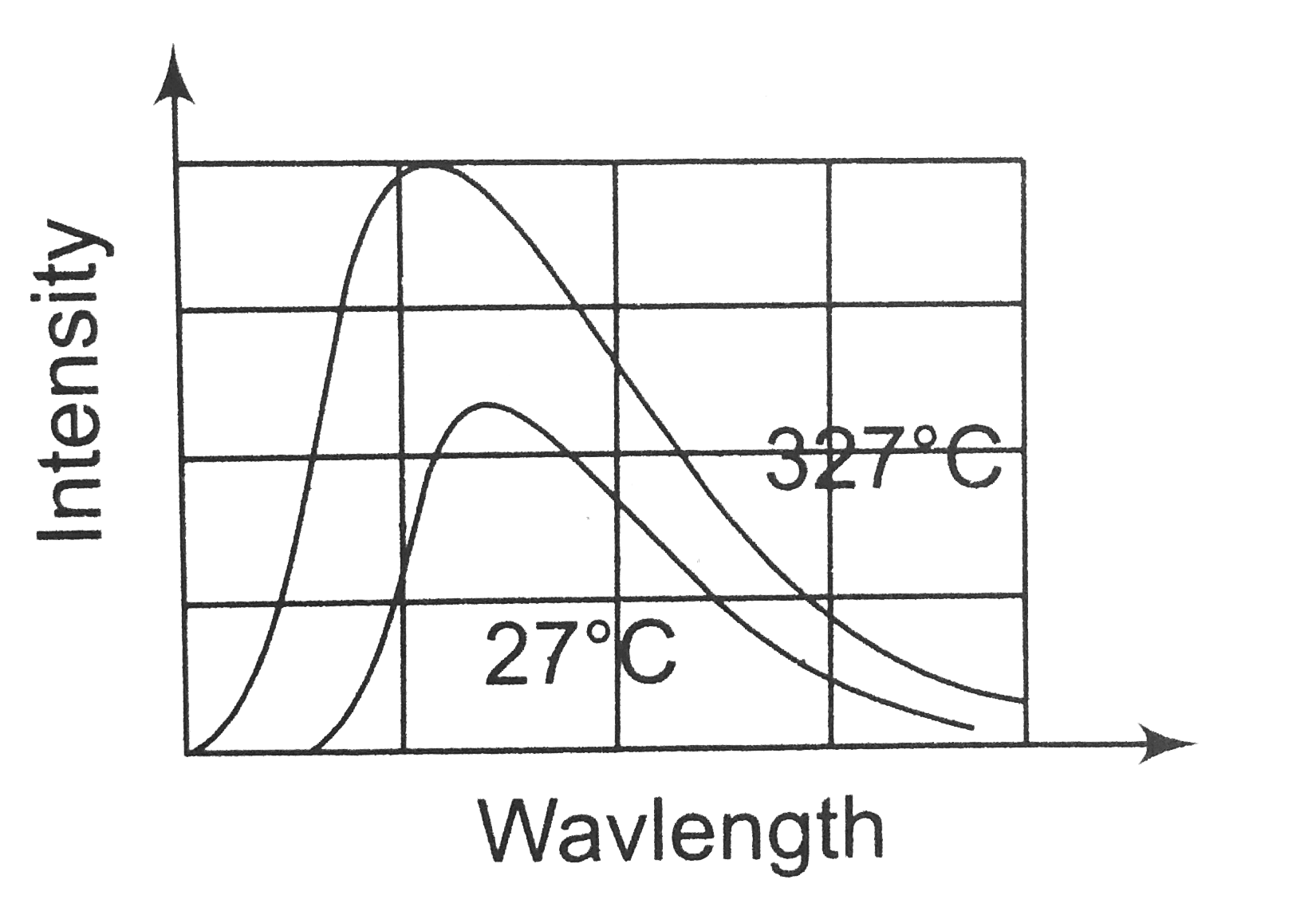
View SolutionThe spectrum of a black body at two temperatures `27^(@)C` and `327^(@)C` is shown in the figure. Let `A_(1)` and `A_(2)` be the areas under the two curves respectively. Find the value of `(A_(2))/(A_(1))`
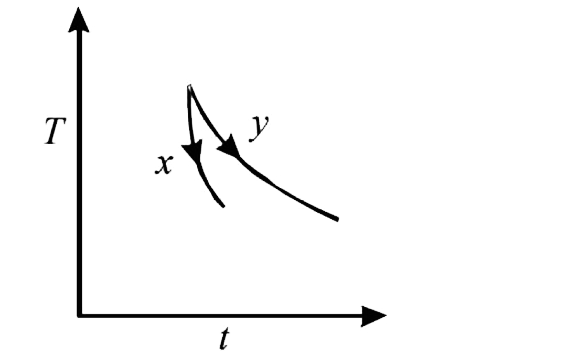
View SolutionThe graph, shown in the adjacent diagram, represents the variation of temperature (T) of two bodies, x and y having same surface area, with time (t) due to the emission of radiation. Find the correct relation between the emissivity and absorptivity power of the two bodies
View SolutionTwo substances `A` and `B` of equal mass m are heated by uniform rate of `6 "cal"s^(-1)` under similar conditions. A graph between temperature and time is shown in figure. Ratio of heat absorbed `H_(A) //H_(B)` by them during complete fusion :-
_E01_076_Q01.png)
View SolutionSunrays are allowed to fall on a lens of diameter 20 cm. They are then brought to focus on a calorimeter containing 20 g of ice. If the absorption by the lens is neglible, the time required to melt all the ice is
(solar constant =`1.9 cal min^(-1) cm^(-2) and L = 80 calg^(-1)`)
View SolutionIf a body coated black at 600K surrounded by atmosphere at 300 K has cooling rate `r_(0)`, the same body at 900 K, surrounded by the same atmosphere, will have cooling rate equal to
View SolutionThe power radiated by a black body is P, and it radiates maximum energy around the wavelength `lambda_(0)`. If the temperature of the black body is now changed so that it radiates maximum energy around a wavelength `3lambda_(0)//4`, the power radiated by it will increase by a factor of
View SolutionIn the figure ABC is a conducting rod whose lateral surfaces are insulated. The length of the section AB is one-half of that of BC, and the respective thermal conductivities of the two sections are as given in the figure. If the ends A and C are maintained at `0^(@)C` and `70^(@)C` respectively, the temperature of junction B in the steady state is

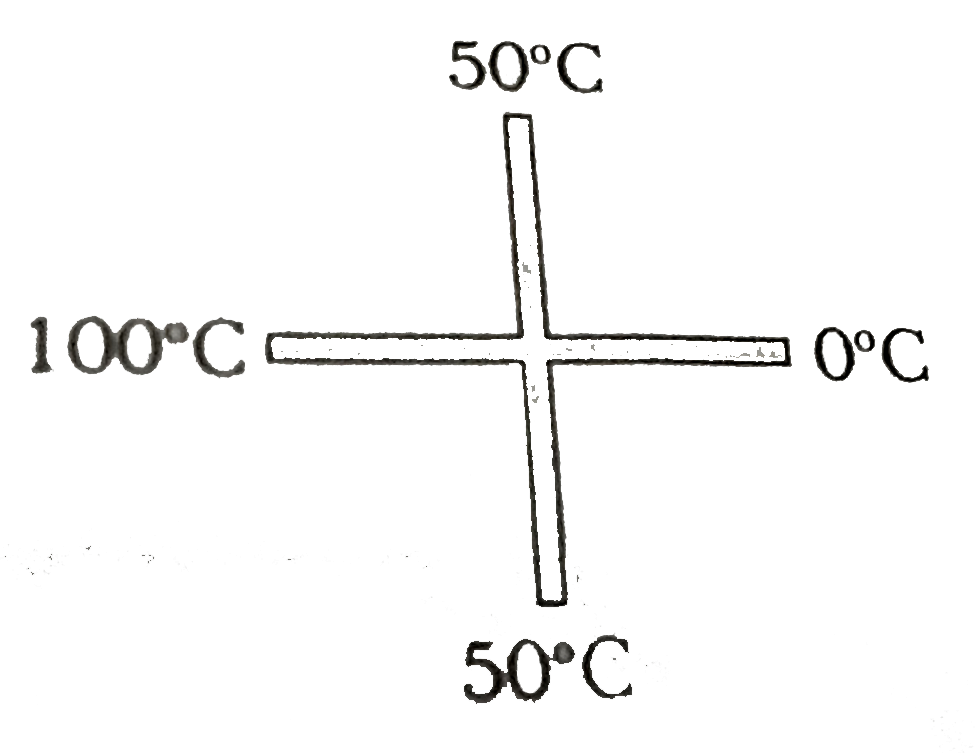
View SolutionTwo similar rods are joined as shown in figure. Then temperature of junction is (assume no heat loss through lateral surface of rod and temperatures at the ends are shown in steady state )
View SolutionFive rods of same dimensions are arranged as shown in the figure. They have thermal conductivities `K _(1) , K_(2) , K _(3) , K_( 4)` and `K_( 5)` . When points A and B are maintained at different temperatures, no heat flows through the central rod if

View SolutionThree identical metal rods `A`, `B` and `C` are placed end to end and a temperature difference is maintained between the free ends of `A` and `C`. If the thermal conductivity of `B(K_(B))` is twice that of `C(K_(C ))` and half that of `A(K_(A))`, `(K_(A)=49w//mK)` calculate the effective thermal conductivity of the system ?
View Solution`0.3 Kg` of hot coffee, which is at `70^(@)C`, is poured into a cup of mass 0.12 kg . Find the final equilibrium temperature. Take room temperature at `20^(@)C` .
(`s_(coffee) = 4080 J/kg-K and s_(cup) = 1020 J/kg-K`.)
View SolutionA calorimeter contains 10 g of water at `20^(@)C`. The temperature falls to `15^(@)C` in 10 min. When calorimeter contains 20 g of water at `20^(@)C`, it takes 15 min for the temperature to becomes `15^(@)C`. The water equivalent of the calorimeter is
View Solution19 g of water at `30^@C` and 5 g of ice at `-20^@C` are mixed together in a calorimeter. What is the final temperature of the mixture? Given specific heat of ice `=0.5calg^(-1) .^(@)C^(-1)` and latent heat of fusion of ice `=80calg^(-1)`
View SolutionWork done in converting 1 g of ice at `-10^@C` into steam at `100^@C` is
View SolutionTwo rigid boxes containing different ideal gases are placed on a table. Box A contains one mole of nitrogen at temperature `T_0`, while Box contains one mole of helium at temperature `(7/3)T_0`. The boxes are then put into thermal contact with each other, and heat flows between them until the gasses reach a common final temperature (ignore the heat capacity of boxes). Then, the final temperature of the gasses, `T_f` in terms of `T_0` is
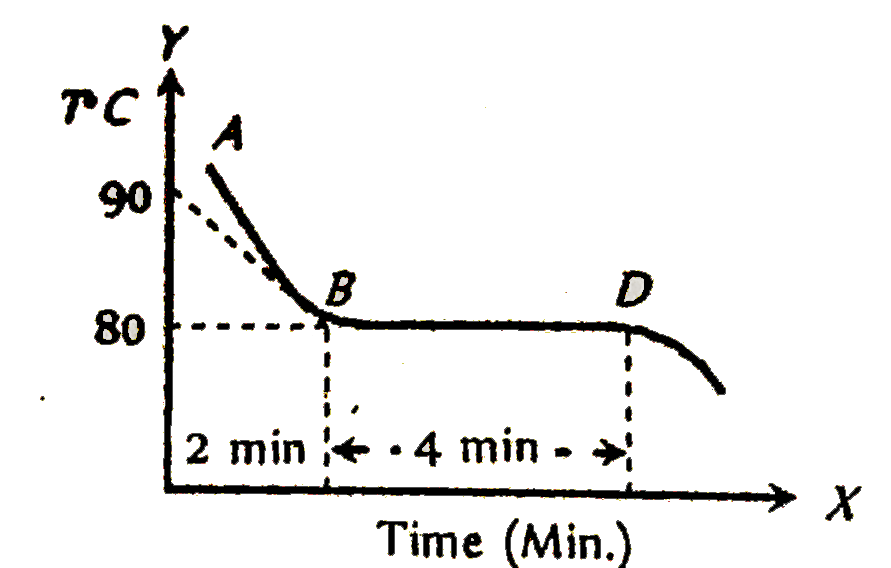
View SolutionThe figure given below shows the cooling curve of pure wax material after heating. It cools from A to B and solidifies along BD . If L and C are respective values of latent heat and the specific heat of the liquid wax, the ratio L / C is
View SolutionThree conducting rods of same material and cross-section are shown in figure. Temperatures of A,D and C are maintained at `20^(@)C, 90^(@)C and 0^(@)C`. The ratio of lengths BD and BC if there is no heat flow in AB is

View SolutionTwo rods with the same dimensions have thermal conductivities in the ratio 1 : 2. they are arranged between heat reservoirs with the same temperature difference, in two different configurations, A and B. The rates of heat flow in A and B are `I_(A) and I_(B)` respectively. The ratio `(I_(A))/I_(B))` is equal to

View SolutionTwo identical conducting rods are first connected independently to two vessels, one containing water at `100^@C` and the other containing ice at `0^@C`. In the second case, the rods are joined end to end and connected to the same vessels. Let `q_1 and q_2` gram per second be the rate of melting of ice in the two cases respectively. The ratio `q_1/q_2` is
(a) `1/2` (b)`2/1` (c)`4/1` (d)`1/4`
View SolutionThree rods of identical area of cross-section and made from the same metal from the sides of an isosceles triangle. ABC, right angled at B. The points A and B are maintained at temperatures T and `sqrt 2T` respectively. In the steady state the temperature of the point C is `T_(C)`.
Assuming that only heat conduction takes place , `T_(C) / T` is equal to
View SolutionTwo identical rods are made of different materials whose thermal conductivities are `K_(1) and K_(2)`. They are placed end to end between two heat reservoirs at temperatures `theta_(1) and theta_(2)`. The temperature of the junction of the rod is

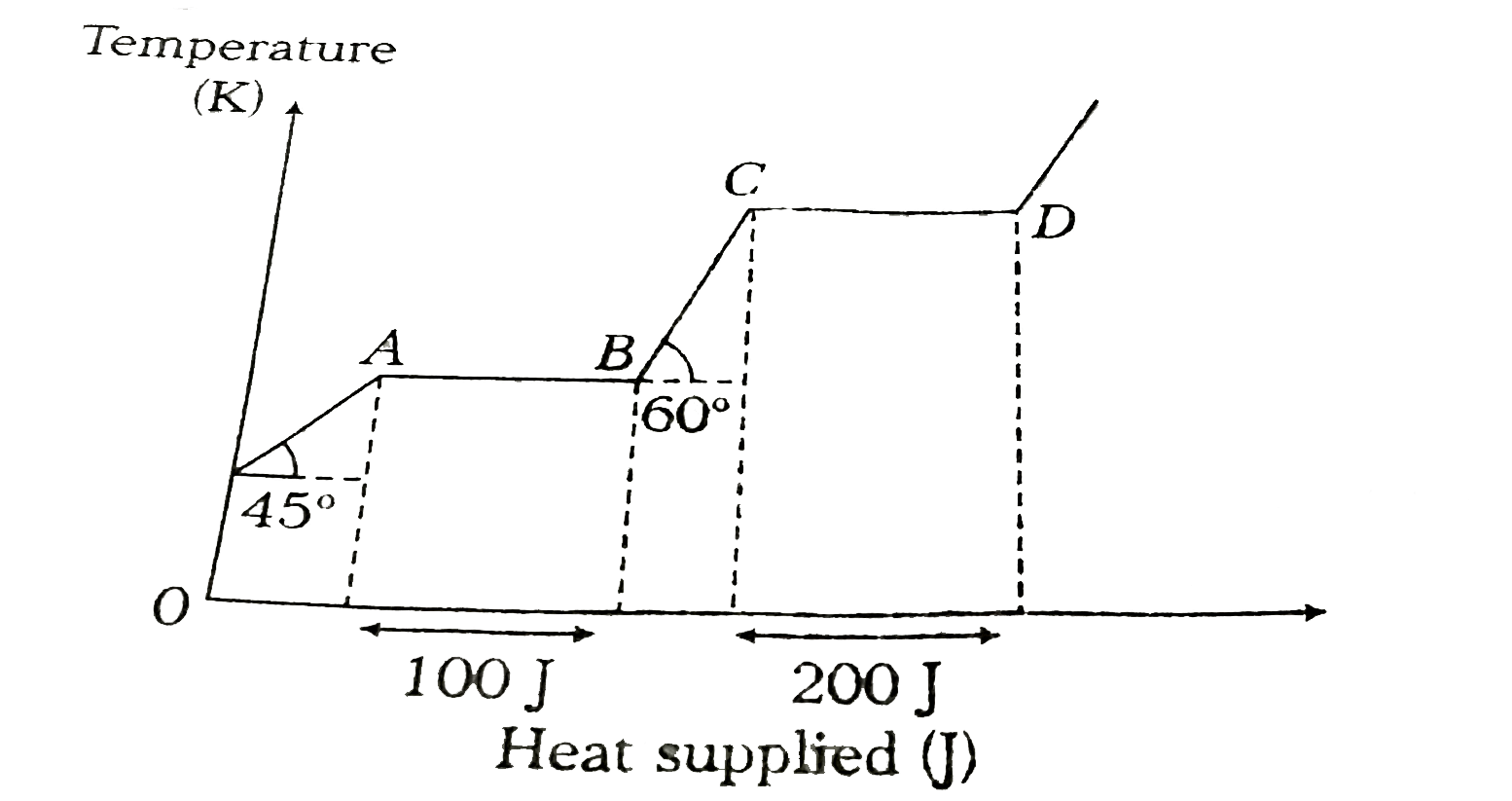
View SolutionThe temperature change versus heat supplied curve is given for 1 kg of a solid block. Then, which of the following statement is/are correct ?
View Solution2kg of ice at `20^@C` is mixed with 5kg of water at `20^@C` in an insulating vessel having a negligible heat capacity. Calculate the final mass of water remaining in the container. It is given that the specific heats of water & ice are `1kcal//kg//^@C` and `0.5`
`kcal//kg//^@C` while the latent heat of fusion of ice is `80kcal//kg`
View Solution10 gm of ice cubes at `0^(@)"C"` are released in a tumbler (water equivalent 55 g) at `40^(@)"C"`. Assuming that negligible heat is taken from the surroundings, the temperature of water in the tumbler becomes nearly` "(L = 80 cal/g)"`
View SolutionA cylindrical metallic rod in thermal contact with two reservation of heat at its two ends conducts an amount of heat `Q` in time `t`. The metallic rod is melted and the material is formed into a rod of half the radius of the original rod. What is the amount of heat conducted by the new rod when placed in thermal contact with the two reservation in time t?
View Solutionif 1 g of steam is mixed with 1 g of ice, then the resultant temperature of the mixture is
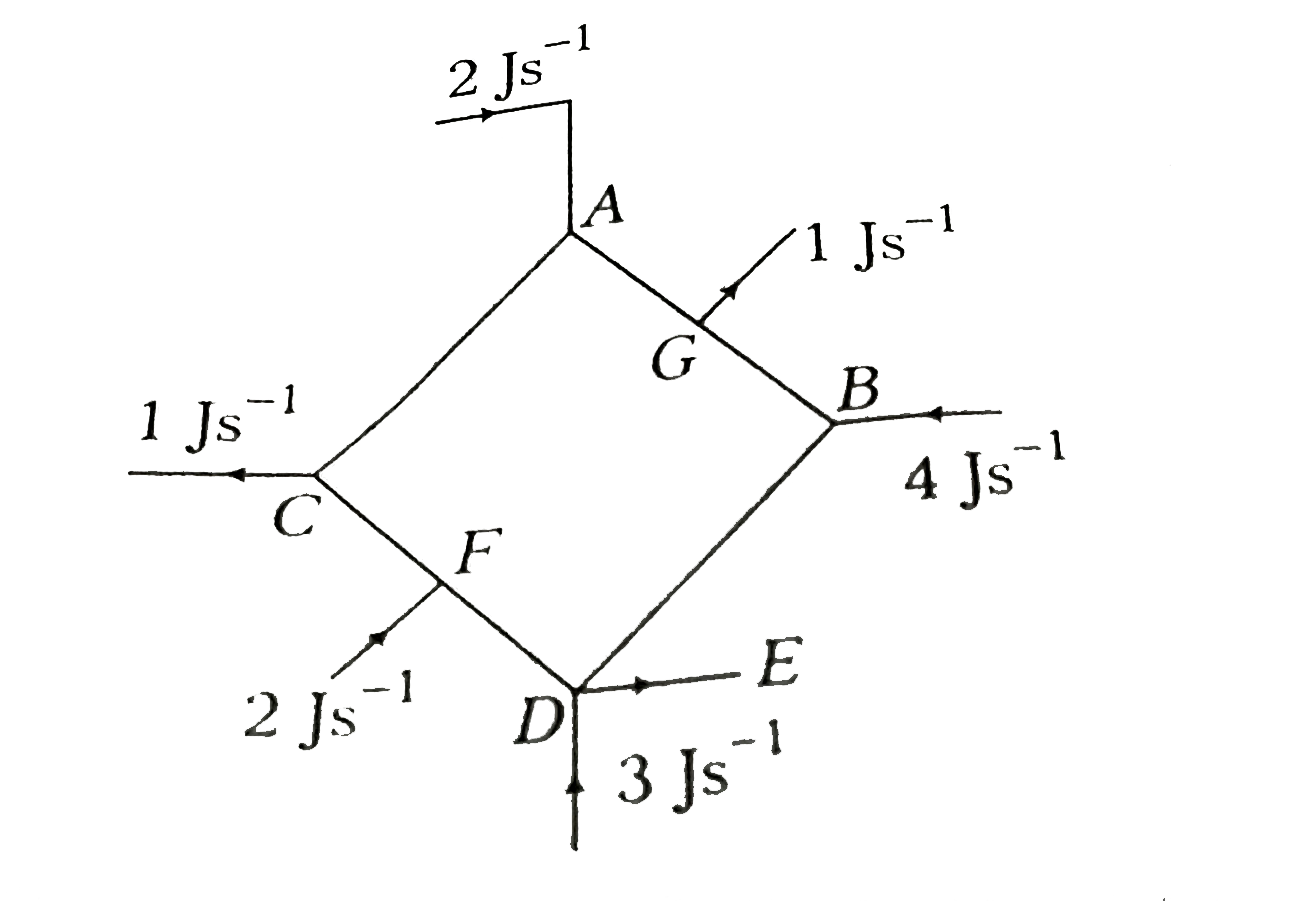
View SolutionThe rate of flow of heat through 12 identical conductors made of same material is shown in the figure. Then, which of the following is correct ?
View SolutionEqual masses of three liquids A, B and C have temperature `10^(@)C, 25^(@)C` and `40^(@)c` respectively. If A and B are mixed, the mixture has a temperature of `15^(@)C`. If B and C are mixed, the mixture has a temperature of `30^(@)C`, if A and C are mixed will have a temperature of
View SolutionIn an industrial process 10 kg of water per hour is to be heated from `20^@C` to `80^@C`. To do this steam at `150^@C` is passed from a boiler into a copper coil immersed in water. The steam condenses in the coil and is returned to the boiler as water at `90^@C`. How many kilograms of steam is required per hour (specific heat of steam`=1 cal//g^@C`, Latent heat of vaporization`=540 cal//g`)?
View SolutionTwo identical conducting rods AB and CD are connected to a circular conducting ring at two diametrically opposite points B and C, the radius of the ring is equal to the length of rods AB and CD. The area of cross-section, thermal conductivity of the rod and ring are equal. points A and D are maintained at temperatures of `100^(@)C` and `0^(@)C`. temperature at poimt C will be

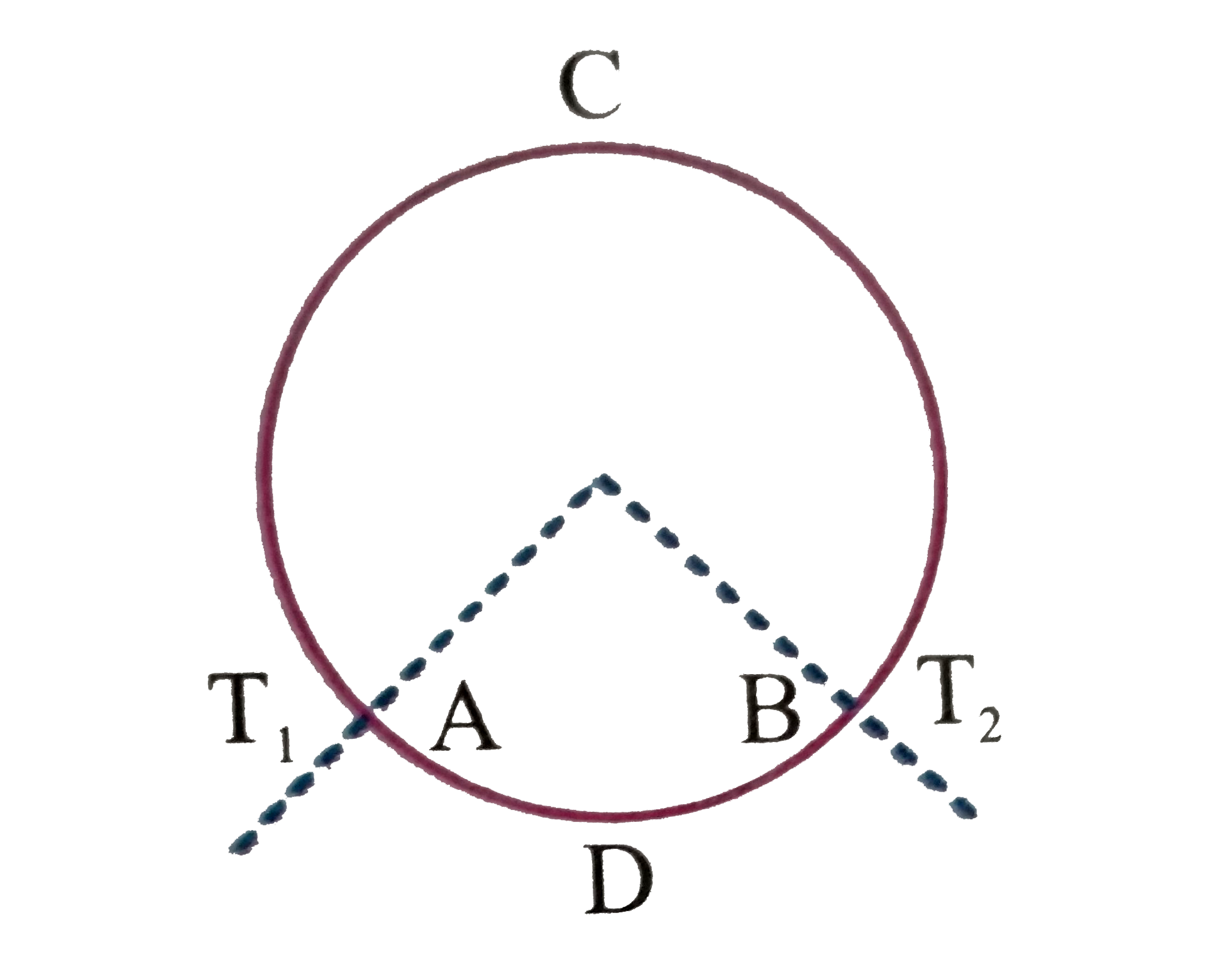
View SolutionA ring consisting of two parts `ADB` and `ACB` of same conductivity k carries an amount of heat `H` The `ADB` part is now replaced with another metal keeping the temperature `T_91)` and `T_(2)` constant The heat carried increases to `2H` What should be the conductivity of the new `ADB` Given `(ACB)/(ADB)=3`
 .
.
View SolutionWater is being boiled in a flat bottomed kettle placed on a stove. The area of the bottom is `300cm^(2)` and the thickness is `2mm`. If the amount of steam produced is `1gm min^(-1)`, then the difference of the temperature between the inner and the outer surface of the bottom is (thermal conductivity of the material of the kettle `0.5calcm^(-1)s^(-1)C^(-1)`, latent heat of the steam is equal to `540calg^(-1))` .
View Solution
Taking it together questions and complete solutions for chapter CALORIMETRY AND HEAT TRANSFER of DC PANDEY PHYSICS (HINGLISH) of Class 11