Complete Solutions to Level 2 Single Correct of chapter CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION |
| DC PANDEY | Level 2 Single Correct |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
A pendulum comsists of a wooden bob of mass `m` and length `l`. A bullet of mass `m_1` is fired towards the pendulum with a speed `v_1` and it emerges from the bob with speed `v_1/3`. The bob just completes motion along a vertical circle. Then `v_1` is
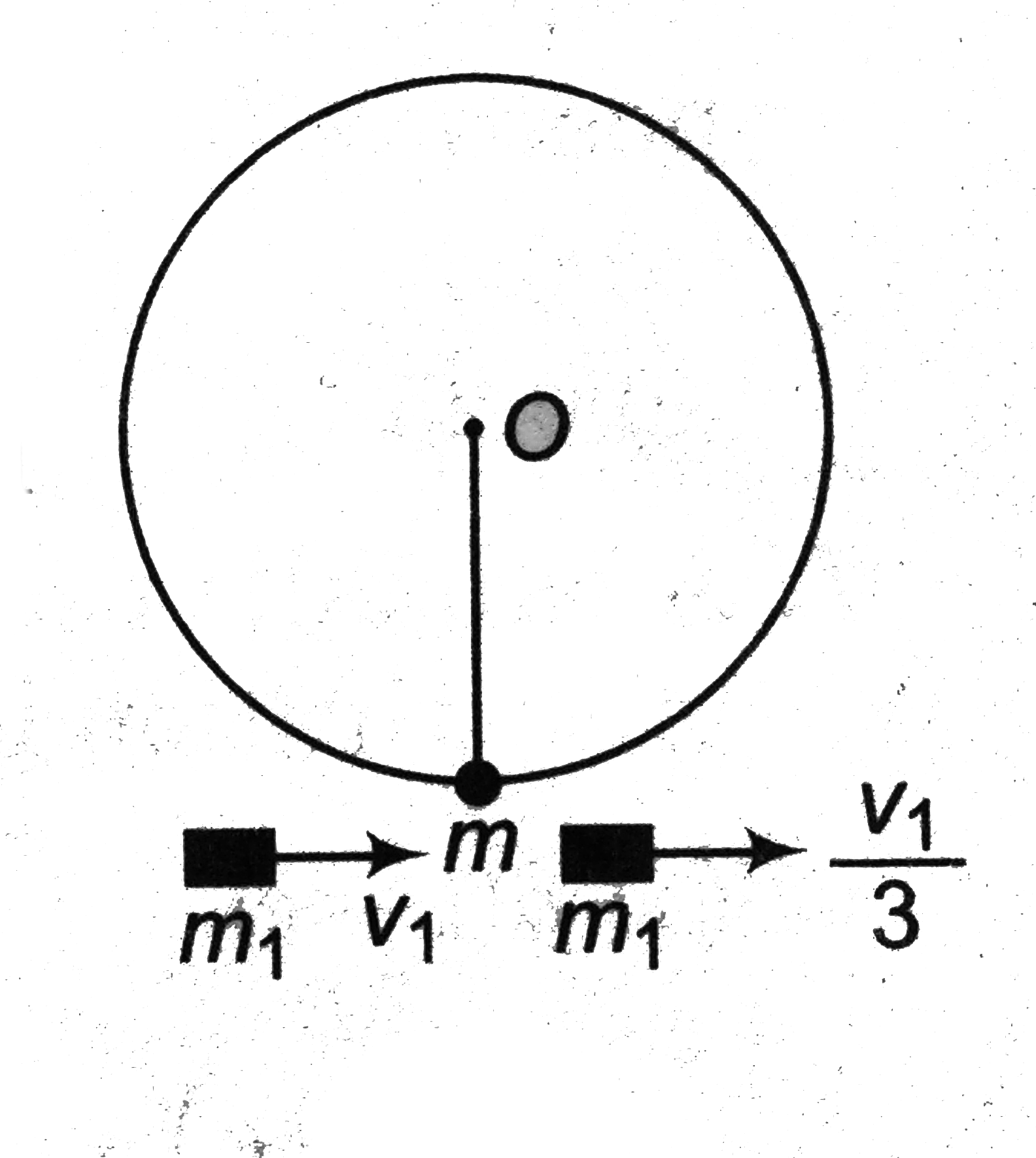 04:52View Solution
04:52View SolutionA bob of mass `m` attached with a string of length `l` tied to a point on ceiling is released from a position when its string is horizontal. At the bottom most point of its motion, an identical mass `m` gently stuck to it. Find the maximum angle from the vertical to which it rotates.
04:35View SolutionA train of mass M is moving on a circular track of radius R with constant speed `v`. The length of the train is half of the perimeter of the track. The linear momentum of the train will be
06:47View SolutionTwo blocks A and B of mass `m` and `2m` are connected together by a light spring of stiffness `k`. The system is lying on a smooth horizontal surface with block A in contact with a fixed vertical wall as shown in the figure. The block B is pressed towards the wall by a distance `x_0` and then released. There is not friction anywhere. If spring takes time `Deltat` to aquire its natural length then average force on the block A by the wall is
 06:19View Solution
06:19View SolutionA striker is shot from a square carom board from a point A exactly at midpoint of one of the walls with a speed of `2ms^-1` at an angle of `45^@` with the x-axis as shown in the figure. The collisions of the striker with the walls of the fixed carom are perfectly elastic. The coefficient of kinetic friction between the striker and board is `0.2`. The coordinate of the striker when it stops (taking point O to be origin) is (in SI units)
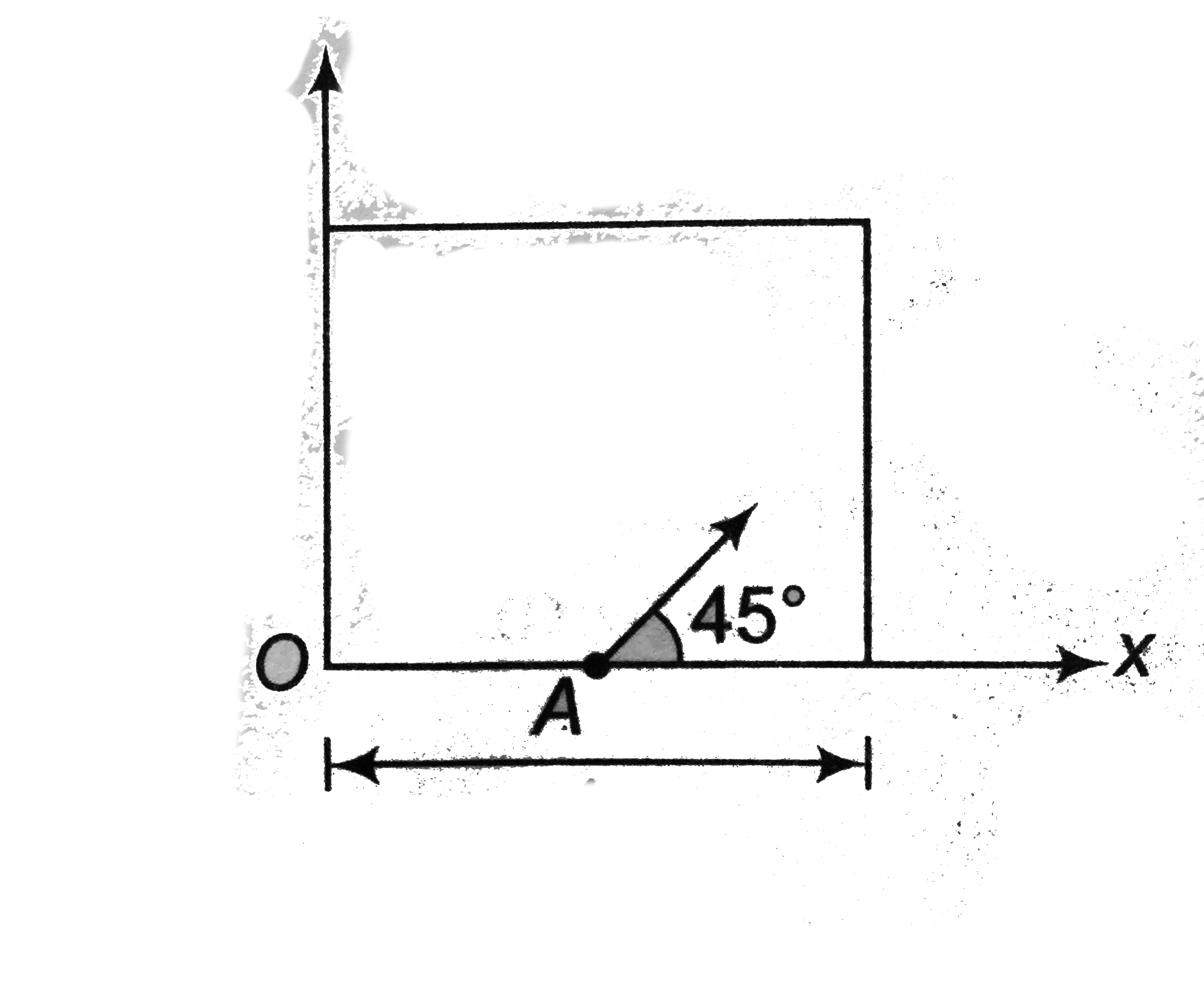 05:33View Solution
05:33View SolutionA ball of mass `1kg` is suspended by an inextensible string `1m` long attached to a point O of a smooth horizontal bar resting on fixed smooth supports A and B. The ball is released from rest from the position when the string makes an angle `30^@` with the vertical. The mass of the bar is `4kg`. The displacement of bar when ball reaches the other extreme position (in m) is
 06:51View Solution
06:51View SolutionA ball falls vertically onto a floor with momentum `p` and then bounces repeatedly. If coefficient of restitution is `e`, then the total momentum imparted by the ball to the floor is
05:14View SolutionA bullet of mass `m`m penetrates a thickness `h` of a fixed plate of mass `M`. If the plate was free to move, then the thickness penetrated will be
06:28View SolutionTwo identical balls of equal masses A and B, are lying on a smooth surface as shown in the figure. Ball A hits the ball B (which is at rest) with a velocity `v=16ms^-1`. What should be the minimum value of coefficient of restitution `e` between A and B so that B just reaches the highest point of inclined plane? `(g=10ms^-2)`
 06:26View Solution
06:26View SolutionThe figure shows a metallic plate of uniform thickness and density. The value of `l` in terms of L so that the centre of mass of the system lies at the interface of the triangular and rectangular portion is
 04:32View Solution
04:32View SolutionParticle A makes a head on elastic collision with another stationary particle B. They fly apart in opposite directions with equal speeds. The mass ratio will be
04:02View SolutionA particle of mass `4m` which is at rest explodes into four equal fragments. All four fragments scattered in the same horizontal plane. Three fragments are found to move with velocity `v` as shown in the figure. The total energy released in the process is
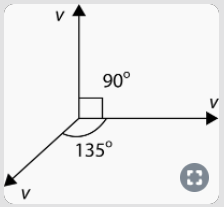 06:24View Solution
06:24View SolutionA ladder of length L is slipping with its ends against a vertical wall and a horizontal floor. At a certain moment, the speed of the end in contact with the horizontal floor is `v` and the ladder makes an angle `theta=30^@` with horizontal. Then, the speed of the ladder's centre of mass must be
05:29View SolutionA body of mass `2g`, moving along the positive x-axis in gravity free space with velocity `20cms^-1` explodes at `x=1m`, `t=0` into two pieces of masses `2//3g` and `4/3g`. After `5s`, the lighter piece is at the point `(3m, 2m, -4m)`. Then the position of the heavier piece at this moment, in metres is
06:36View SolutionA body of mass `m` is dropped from a height of `h`. Simultaneously another body of mass `2m` is thrown up vertically with such a velocity `v` that they collide at height `h/2`. If the collision is perfectly inelastic, the velocity of combined mass at the time of collision with the ground will be
05:52View SolutionA man is standing on a cart of mass double the mass of man. Initially cart is at rest. Now, man jumps horizontally with velocity `u` relative to cart. Then work done by man during the process of jumping will be
 06:16View Solution
06:16View SolutionTwo balls of equal mass are projected upwards simultaneously, one from the ground with initial velocity `50ms^-1` and the other from a `40m` tower with initial velocity of `30ms^-1`. The maximum height attained by their COM will be
04:33View SolutionA particle of mass `m` and momentum `p` moves on a smooth horizontal table and collides directly and elastically with a similar particle (of mass m) having momentum `-2p`. The loss `(-)` or gain `(+)` in the kinetic energy of the first particle in the collision is
04:46View SolutionAn equilateral triangular plate of mass `4m` of side a is kept as shown. Consider two cases: (i) a point mass `4m` is placed at the vertex P of the plate (ii) a point mass `m` is placed at the vertex R of the plate. In both cases the x-coordinate of centre of mass remains the same. Then x coordinate of centre of mass of the plate is
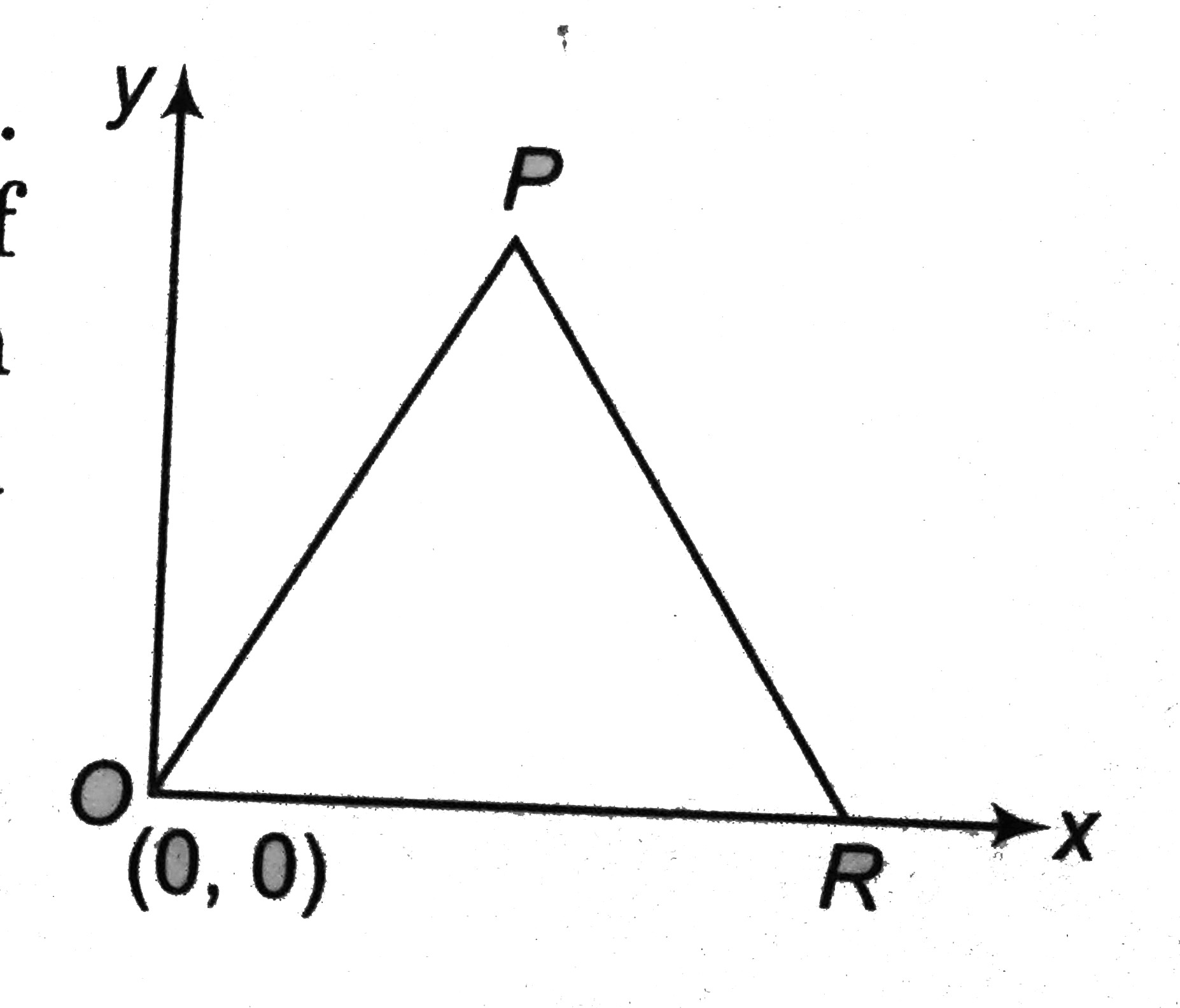 06:14View Solution
06:14View SolutionFour cubes of side `a` each of mass `40g`, `20g`, `10g` and `20g` are arranged in XY plane as shown in the figure. The coordinates of COM of the combination with respect to point O is
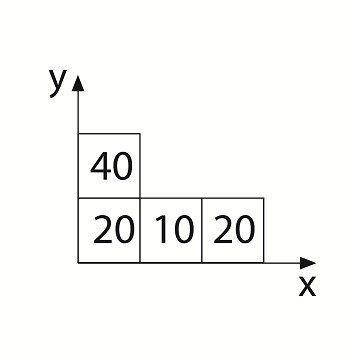 04:56View Solution
04:56View SolutionA particle of mass `m_0`, travelling at speed `v_0`. Strikes a stationary particle of mass `2m_0`. As a result of the particle of mass `m_0` is deflected through `45^@` and has a final speed of `v_0/sqrt2`. Then the speed of the particle of mass `2m_0` after this collision is
03:06View SolutionTwo bars of masses `m_1` and `m_2` connected by a weightless spring of stiffness `k`, rest on a smooth horizontal plane. Bar `2` is shifted by a small distance `x_0` to the left and released. The veloicyt of the centre of mass of the system when bar 1 breaks off the wall is
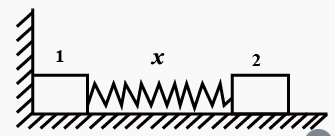 04:45View Solution
04:45View Solution`n` elastic balls are placed at rest on a smooth horizontal plane which is circular at the ends with radius `r` as shown in the figure. The masses of the balls are `m`, `m/2`, `m/2^2`, …………….`(m)/(2^(n-1))` respectively. What is the minimum velocity which should be imparted to the first ball of mass `m` such that `n^th` ball completes the vertical circle
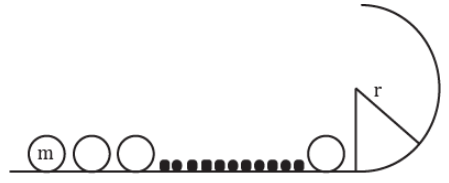 05:48View Solution
05:48View Solution
Level 2 Single Correct questions and complete solutions for chapter CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- Example
- Exercise 11.1
- Exercise 11.2
- Exercise 11.3
- Exercise 11.4
- Exercise 11.5
- Exercise 11.6
- Level 1 Objective
- Level 1 Subjective
- Level 1 Subjective Questions
- Level 2 Comprehension Based
- Level 2 Comprehension Based Questions
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Single Correct Option
- Level 2 Subjective
- MiscellaneousExamples
- Solved Examples
- Type 1
