Complete Solutions to Bohr s Theory of chapter ATOMIC STRUCTURE of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | ATOMIC STRUCTURE |
| GRB PUBLICATION | Bohr s Theory |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The potential energy of the electron present in the ground state of ` Li^(2+)` ion is represented by :
View SolutionIf radius of ground state of H- atom (according to Bohr' model) is 'R' then radius of `3^(rd)` energy state of `Li^(+2)` is :
View SolutionIn a certain electronic transition in the hydrogen atoms from an initial state `(1)` to a final state `(2)`, the difference in the orbit radius `((r_(1)-r_(2))` is 24 times the first Bohr radius. Identify the transition-
View Solutionthe energy levels for ` A^(+z=-1)` can be given by :
View SolutionThe radii of two of the first four Bohr's orbits of the hydrogen atom are in the ratio ` 1: 4`. The energy difference between them may be :
View SolutionThe velocity of electrons in the ground state of H- atom is `2.185 xx 10^(8)` cm/sec . The velocity of electron in the first excited state of `Li^(2+)` ion in cm/sec would be :
View SolutionThe ratio of the radius of two Bohr's orbit of `Li^(+2)` is `1:9`. What would be their nomenclature.
View SolutionThe ratio of radius of first orbit in hydrogen to the radius of first orbit in deuterium will be :
View SolutionFor H-atoms , the energy required for the removal of electron from various sub-shells is given as under :
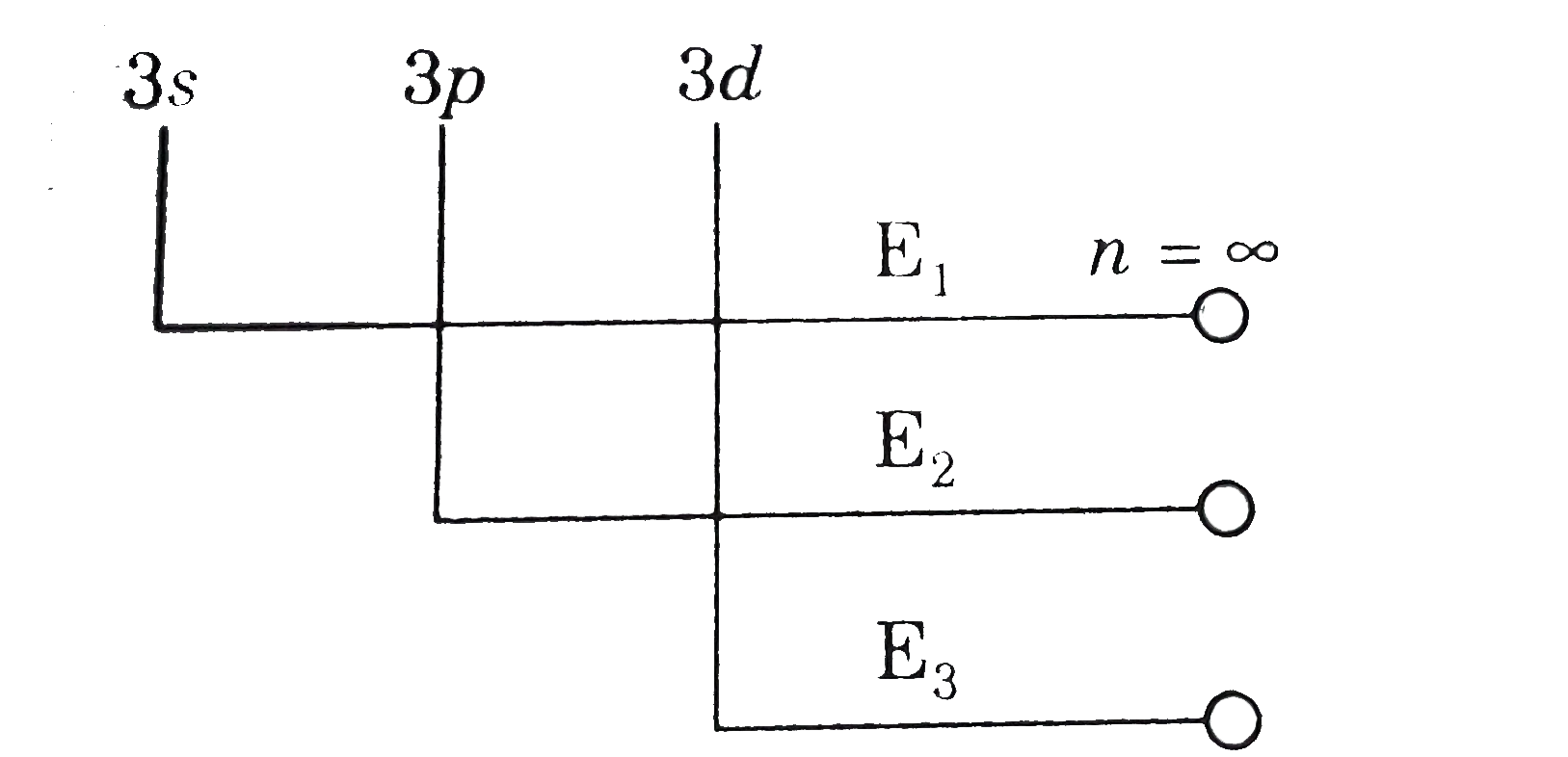
The order of the energies would be :
View SolutionWhich of the following options is incorrect regarding Bohr's Model of an atom ?
View SolutionWhich of the following transition will have a wavelength different than that observed in rest of the transitions ?
View SolutionA substance absorbs electromagnetic radiations of wavelength 12.3 nm and then emits another electromagnetic radiations of wavelength 24.6 nm . If ratio of number of photons absorbed to number of photons emitted is `2:1` then ratio of energy absorbed to energy emitted will be :
View SolutionA unielectronic species is in some excited state 'A' and on absorbing a photon of energy 'x' eV gets promoted to a new state 'B' . On de-excitation back to the ground state a total of 10 different wavelengths were emitted in which seven have energy greater than 'x' eV . What will be the ionisation energy ?
View SolutionThe radii of two Bohr's orbits of hydrogen atom are in the ratio of `4:9` . Which of the following value of energy difference is not possible between the two orbits? [I.E . = 13.6 eV]
View SolutionIn a hypothetical model of an atoms following Bohr's theory, the potential energy is given by potential energy `=-(Ke^(2))/(4r^(4))`. Which of the following options will be correct ? (Symbols have usual meaning)
View SolutionThe time period of revolution in the 3rd orbit of `Li^(2+)` ions is x sec . The time period of revolution in the 2 nd orbit of `He^(+)` ion , should be :
View SolutionThe charge on the electron and proton in reduced to half . Let the present value of the Rydberg constant is R . What will be the new value of the Rydberd constant ?
View SolutionA hydrogen like species with atomic number Z is present in a higher excited state (n) . This electron can make transition to the first excited level by successively emitting two photons of energy 2.64 eV and 48.36 eV . This electron can also make transition to third excited state by emitting three photons of energy 2.64 eV , 2. 66 eV and 4.9 eV .
Identify the hydrogen like species involved .
View SolutionThe ratio of `(E_(2) - E_(1))` to `(E_(4) - E_(3))` for `He^(+)` ion is approximately equal to (where `E_(n)` is the energy of nth orbit ):
View Solution`1^(st)` excitation Potential of a hydrogen like sample is 15 volt. If all the atoms of the sample are in `2^(nd)` excited state then find the `K.E.` in `eV` of the electron ejected if a photon of energy `(65)/(9)eV` is supplied to this sample.
View SolutionIf the ionization energy of `He^(+)` is `19.6xx10^(-18) J` per atom then the energy of `Be^(3+)` ion in the second stationary state is `:`
View SolutionThe binding energy of `e^(-)` in ground state of hydrogen atom is 13.6 eV . The energies required to eject out an electron from three lowest states of `He^(+)` atom will be (in eV):
View SolutionCorrect order of radius of the first orbit of `H, He^+, Li^(2 +), Be^(3 +)` is :
View SolutionWhat is likely to be principal quantum number for a circular orbit of diameter `20nm` of the hydrogen atom if we assume Bohr orbit be the same as that represented by the principal quantum number?
(a). `10`
(b). `14`
(c). `12`
(d). `16`
View SolutionWhich of the correct relationship?
View SolutionIf the value of `E=-78.4 "kcal/mol"`, the order of the orbit in hydrogen atom is-
View SolutionIf velocity of an electron in 1st orbit of H atoms is V , what will be the velocity in 3rd orbit of `Li^(2+)` ?
View SolutionIn a certain electronic transition in the hydrogen atoms from an initial state `(1)` to a final state `(2)`, the difference in the orbit radius `((r_(1)-r_(2))` is 24 times the first Bohr radius. Identify the transition-
View SolutionThe species which has its fifth ionization potential equal to 340 V is :
View SolutionIn hydrogen atom an whit has a diemeter of about `16.92Å` .What in the maximum number of electron that can be accommodated ?
View SolutionRatio of frequency of revolution of electron in the second state of `He^(o+)` revolution of electron in the second state `He^(Theta)` and second state of hydrogen is
View SolutionThe number of waves in the fourth bohr orbit of hydrogen is
View SolutionAn excited hydrogen atom returns to the ground state . The wavelength of emitted photon is ` lambda` The principal quantum number of the excited state will be :
View SolutionWhat is the separation energy (in eV ) for `Be^(3+)` in the first excited state ?
View SolutionWhen an electron makes a transition from `(n + 1)` state to n state the frequency of emitted radiation is related to n according to `(n gtgt 1)`
View SolutionWhich of the following statements is wrong for H-like atom ?
View SolutionThe angular momentum of electron in an excited H atom is `(h)/(pi)` . The P.E. of electron will be :
View SolutionPotential energy of electron present in 2nd orbit of `Li^(2+)` is :(`r_(0)` = Radius of 1st Bohr's orbit )
View SolutionThe maximum energy is present in any electron at
View SolutionWhen electron in a Bohr atom is excited then which of the following increases?
View SolutionGiven `DeltaH` for the process `Li(g)rarrLi^(+3)(g) + 3e^(-)` is `19800kJ//"mole" & IE_(1)` for `Li` is `520` then `IE_(2) & IE_(1)` of `Li^(+)` are respectively (approx value) :-
(a). `11775,7505`
(b). `19280,520`
(c). `11775,19280`
(d). data insufficient
View SolutionFor a valid Bohr orbit , its circumference should be :
View SolutionLet the I.E. of hydrogen like species be 320 eV . Find out the value of quantum number having the energy equal to `-20` eV .
View SolutionAngular momentum for P-shell electron is :
View SolutionThe energy of an electron in the first Bohr orbit is `-13 eV` . The energy of `Be^(3+)` in the first excited state is :
View SolutionHow do the energy gaps between successive electron energy levels in an atom very from low to high n values ?
View SolutionIn a hydrogen atom , which transition produces a photon with the highest energy ?
View Solution`S_(1)` : Bohr model is applicable for `Be^(2+)` ion .
`S_(2)` : Total energy coming out of any light source is integral multiple of energy of one photon.
`S_(3)` : Number of waves present in unit length if wave number .
`S_(4)` : e/m ratio in cathode ray experiment is independent of the nature of the gas .
Select the correct set of True-False for above statement.
View Solution`S_(1)` : Potential energy of the two opposite charge system increase with the decrease in distance .
`S_(2)` : When an electron makes transition from higher orbit to lower orbit it's kinetic energy increases.
`S_(3)` : When an electron make transition from lower energy to higher energy state its potential energy increases.
`S_(4)` : 11 eV photon can free an electron from 1 st excited state of `He^(+)` ion .
Select the correct set of true-false for above statements.
View SolutionThe energy of hydrogen atom in its ground state is `-13.6 eV`. The energy of the level corresponding to the quantum number `n = 5` is
View SolutionThe wave number of electromagnetic radiations emitted during the transition of electron in between two levels of `Li^(2+)` ion having sum of the principal quantum numbers 4 and difference is 2 ,will be:
(`R_(H)` = Rydberg constant )
View SolutionIn Bohr's model of the hydrogen atom the ratio between the period of revolution of an electron in the orbit of `n=1` to the period of the revolution of the electron in the orbit `n=2` is :-
(a). `1 : 2`
(b). `2 : 1`
(c). `1 : 4`
(d). `1 : 8`
View SolutionIn an atom, two electrons move around nucleus in circular orbits of radii ( R) and ( 4R) . The ratio of the time taken by them to complete one revolution is :
View SolutionIf first ionisation potential of a hypothetical atom is `16 V`, then the first excitation potential will be :
View SolutionThe angular momentum of electron in a given orbit is J . Its kinetic energy will be :
View SolutionAccording to Bohr's model of hydrogen atom the electric current generated due to motion of electron in nth orbit is :
View SolutionIn a sample of H-atoms , electrons de-excite from a level 'n' to 1 . The total number of lines belonging to Balmer series are two . If the electrons are ionised from level 'n' by photons of energy 13 eV . Then the kinetic energy of the ejected photoelectrons will be :
View SolutionThe orbit having Bohr radius equal to 1st Bohr orbit of H-atom is :
View SolutionEnergy of H-atom in the ground state is `-13.6eV`. Hence energy in the second excited state is
View SolutionThe wavelength of the radiation emitted , when in a hydrogen atom electron falls from infinity to stationary state 1 , would be :
(Rydberg constant = `1.097 xx 10^(7) m^(-1)`)
View SolutionAccording to Boohr's theory the angular momentum of an electron in 5th orbit is :
View SolutionThe ionization enthalpy of hydrogen atom is `1.312 xx 10^6 J mol^-1`. The energy required to excite the electron in the atom from `n= 1` to `n = 2` is :
View SolutionWhen `Z` is doubled in an atom, which of the following statements are consistent with Bohr's theory ?
View SolutionIonization energy of a hydrogen-like ion A is greater than that of another hydrogen like ion B . Let r, u, E and L represent the radius of the orbit , speed of the electron , total energy of the electron and angular momentum of the electron respectively (for the same n ). In ground state :
View SolutionThe potential energy of the electron present in the ground state of ` Li^(2+)` ion is represented by :
View SolutionPhotons of equal energy were incident on two different gas samples. One sample containing H-atoms in the ground state and the other sample containing H-atoms in some excited state with a principle quantum number 'n'. The photonic beams totally ionise the H-atoms. If the difference in the kinetic energy of the ejected electrons in the two different cases is `12.75 eV`. Then find the principal quantum number 'n' of the excited state.
View SolutionThe potential energy of the electron present in the ground state of ` Li^(2+)` ion is represented by :
View SolutionWhich transition in `Li^(2 +)` would have the same wavelength as the `2 rarr 4` transition in `He^(+)` ion ?
View SolutionSuppose a gaseous mixtures of `He, Ne, Ar ` and `Kr` is irradiated with photons for frequency appropriate to ionize Ar, What ions will be present in the mixture ?
View SolutionThe kinetic energy of an electron in the second Bohr orbit of a hydrogen atom is [`a_0` is Bohr radius] :
View SolutionThree photons originating from excited atomic hydrogen atoms are found to have energies of 0.66 eV , 1.89 eV and 2.55 eV respectively . The minimum no. of atoms that must be present are :
View SolutionThe velocity of electrons in the 3rd excited state of a hydrogen atom is [`a_(0)` is Bohr radius ]:
View SolutionWhich of the following is the energy of a possible excited state of hydrogen?
View SolutionWavelength of radiation emitted when an electron jumps from a state A and C is `3000 "Å"` and it is `6000"Å"` when the electron jumps from state B to C . Wavelength of the radiation emitted when an electron jumps from state A to B will be :
View SolutionDifference in wavelength of two extreme lines of Lyman series in emission spectrum of `He^(+)` would be :
View SolutionA collection of H-atoms in 9th excited state returns to ground state . Calculate ratio of total number of spectral lines emitted without emitting any line in Brackett series to number of Brackett series lines .
View SolutionLast line of Lyman series for `H-` atom has wavelength `lambda_(1) A,2^(nd)` line of Balmer series has wavelength `lambda_(2)A` then
View SolutionFor the Hydrogen spectrum , last line of the Lyman series has frequency `v_(1)` , last line of Lyman series of `He^(+)` ion has frequency `v_(2)` and last line of Balmer series of
View SolutionThe number of possible line of Paschen series when electron jumps from seventh excited state up to ground state (in hydrogen like atom) is :
View SolutionThe wave number of the first line of Balmer series of hydrogen is `15200 cm ^(-1)` The wave number of the first Balmer line of `Li^(2+)` ion is
View SolutionThe shortest wavelength in Lyman series of `Li^(2+)` ion is :
View SolutionWhat hydrogen-like ion has the wavelength difference between the first lines of Balmer and Lyman series equal to `59.3 nm`? `R_(H) = 109678 cm^(-1)`
View SolutionThe longest wavelength of the Lyman series for Hydrogen atom is the same as the wavelength of a certain line in the spectrum of `He^(+)` when the electron makes a transition from `n to 2` .The value of n is :
View SolutionRatio of wavelength of series limit of Paschen and Brackett series for a single electronic species is :
View SolutionWhen electron are de-exciting from nth orbit of hydrogen atoms to ground state, 15 spectral lines are formed . The shortest wavelength among these will be :
View SolutionTotal no of lines in Lyman series of H spectrum will be-
(where n=no. of orbits)
View SolutionThe wavelngth fo a spectrl line for an electronic transition is inversely related to :
View SolutionNumber of visible lines when an electron returns from 5th orbit to ground state in H spectrum :
View SolutionIn a sample of `H-` atom electrons make transition from `5^(th)` excited state to ground state, producing all possible types of photons, then number of lines in infrared region are
View SolutionSuppose that a hypothetical atom gives a red, green, blue and violet line spectrum. Which jump according to figure would give off the red spectral line.
 .
.
View SolutionThe difference between the wave number of 1st line of Balmer series and last line of Paschen series for `Li^(2+)` ion is :
View SolutionWhat would be the maximum number of emission lines for atomic hydrogen that you would expert to see with the naked eye if the only electronic energy involved are those as shown in figure ?

View SolutionMonochromatic radiation of wavelength `lambda` is incident on a hydrogen sample in ground state. Hydrogen atoms absorb a fraction of light and subsequently emit radiations of six different wavelength . Find the wavelength `lambda`.
View SolutionWhich electronic transition in atomic hydrogen corresponds to the emission of visible light ?
View SolutionThe wave number of the first line of Balmer series of hydrogen is `15200 cm ^(-1)` The wave number of the first Balmer line of `Li^(2+)` ion is
View SolutionLet `nu_(1)` be the frequency of the series limit of the lyman series `nu_(2)` be the frequency of the first line of th lyman series and `nu_(3)` be the frequency of the series limit of the Balmer series. Then
View SolutionWave number of spectral line for a given transition is `x cm^(-1)` for `He^(+)`, then its value for `Be^(3+)` (isoelectronic of `He^(+))` for same transition is:
View SolutionAn atom has x energy level , then total number of lines in its spectrum are :
View SolutionThe ratio of wavelength of photon corresponding to the `alpha`-line of Lyman series in H-atom and `beta`- line of Balmer series in `He^(+)` is :
View SolutionIf the shortest wavelength of H-atom in Lyman series is `x`, then longest wavelenght in Balmer series of `He^(2+)` is :
View Solution
Bohr s Theory questions and complete solutions for chapter ATOMIC STRUCTURE of GRB CHEMISTRY (HINGLISH) of Class 11