Complete Solutions to Comprehesion Type of chapter ATOMIC STRUCTURE of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | ATOMIC STRUCTURE |
| GRB PUBLICATION | Comprehesion Type |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
Read the following passage carefully and answer the questions

The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's `alpha-`scattering experiment. If an `alpha-`perticle is projected from infinity with speed v, towards the nucleus having z protons then the `apha-`perticle which is reflected back or which is deflected by `180^(@)` must have approach closest to the nucleus. It can be approximated that `alpha-`particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
`("Total Energy")_("initial") = ("Total Enregy")_("final")`
`(KE)_(i) +(PE)_(i)=(KE)_(f)+(PE)_(f)`
`(PE)_(i) =0, "since"PE` of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
`1/2m_(alpha)v_(alpha)^(2) + 0=0 + (kq_(1)q_(2))/(R)`
`rArr1/2m_(alpha)v_(alpha)^(2)=k(2exxze)/(R)rArrR=(4kze^(2))/(m_(alpha)v_(alpha)^(2)`
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
`R=R_(0)(A)^(1//3)`
where `R_(0) = 1.2xx10^(-15)m`
A= atomic mass number
R=radius of nucleus
If the diameter of two different nuclei are in the ratio 1:2 then their mass number are in the ratio:
View SolutionRead the following passage carefully and answer the questions
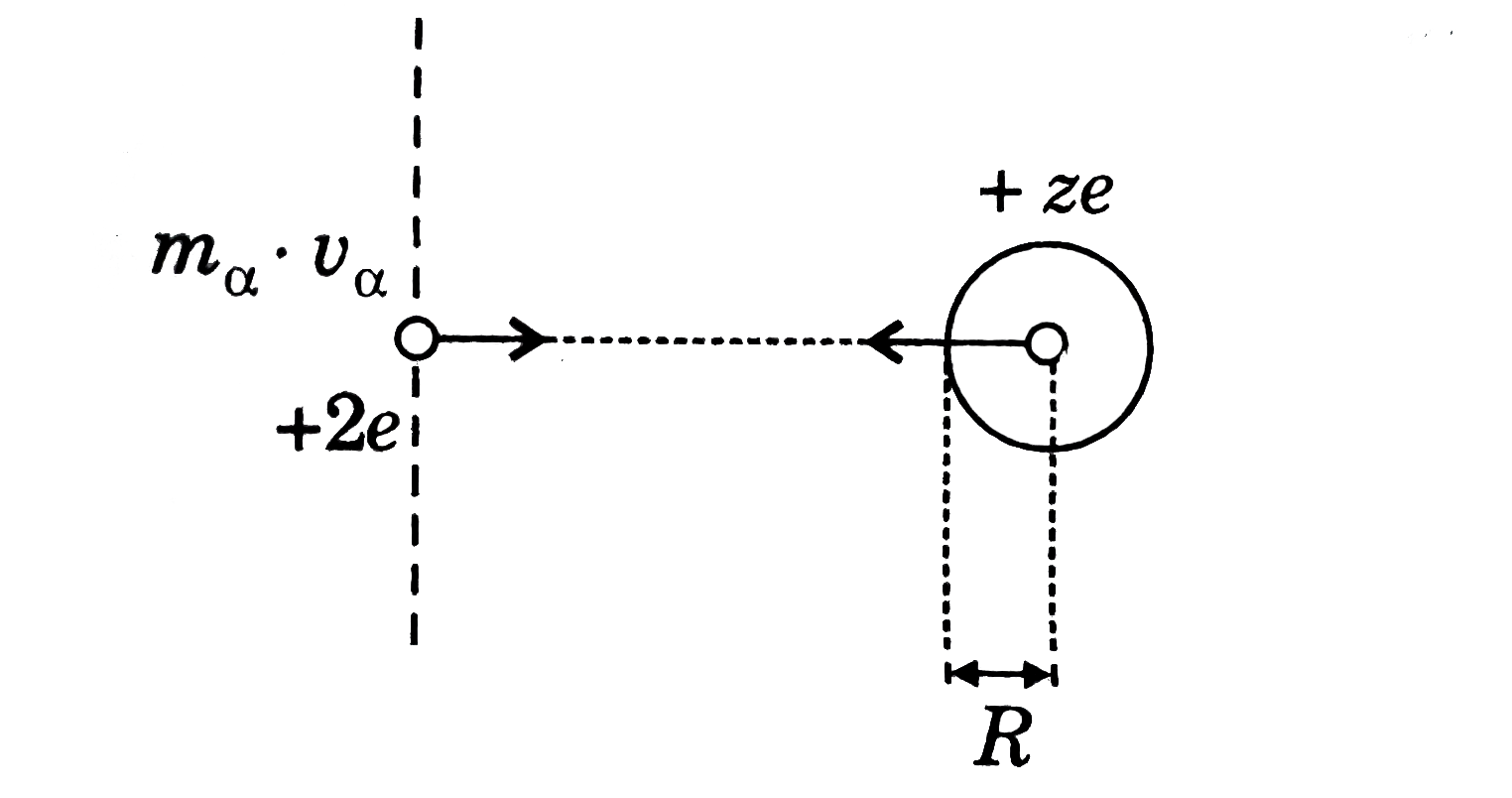
The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's `alpha-`scattering experiment. If an `alpha-`perticle is projected from infinity with speed v, towards the nucleus having z protons then the `apha-`perticle which is reflected back or which is deflected by `180^(@)` must have approach closest to the nucleus. It can be approximated that `alpha-`particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
`("Total Energy")_("initial") = ("Total Enregy")_("final")`
`(KE)_(i) +(PE)_(i)=(KE)_(f)+(PE)_(f)`
`(PE)_(i) =0, "since"PE` of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
`1/2m_(alpha)v_(alpha)^(2) + 0=0 + (kq_(1)q_(2))/(R)`
`rArr1/2m_(alpha)v_(alpha)^(2)=k(2exxze)/(R)rArrR=(4kze^(2))/(m_(alpha)v_(alpha)^(2)`
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
`R=R_(0)(A)^(1//3)`
where `R_(0) = 1.2xx10^(-15)m`
A= atomic mass number
R=radius of nucleus
If `alpha-`particle with speed `v_(0)` is projected from infinity and it approaches upto `r_(0)` distance from the nuclei. Then the speed of `alpha-`particle which approaches `2r_(0)` distance from the nucleus is
View SolutionRead the following passage carefully and answer the questions
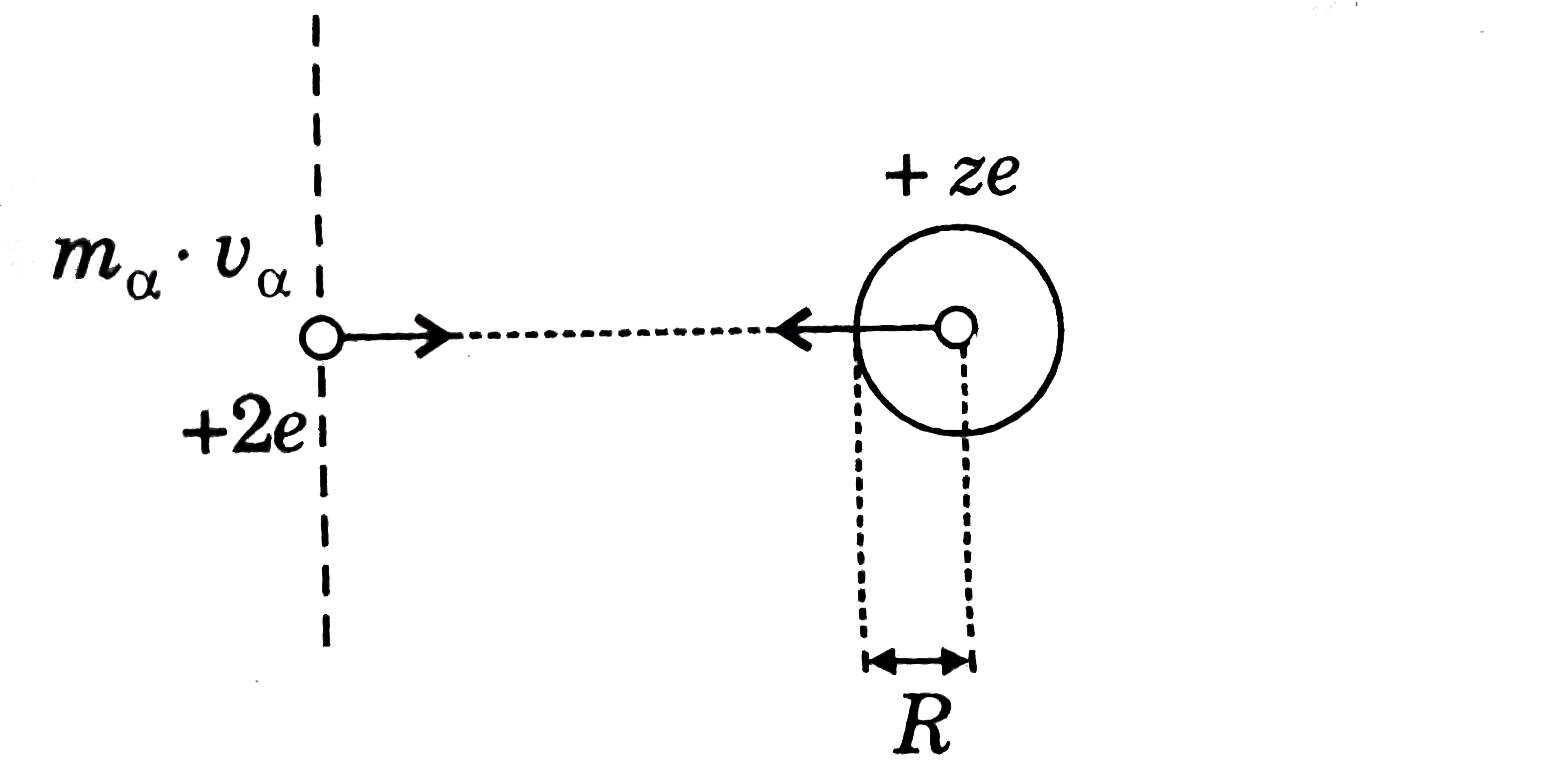
The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's `alpha-`scattering experiment. If an `alpha-`perticle is projected from infinity with speed v, towards the nucleus having z protons then the `apha-`perticle which is reflected back or which is deflected by `180^(@)` must have approach closest to the nucleus. It can be approximated that `alpha-`particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
`("Total Energy")_("initial") = ("Total Enregy")_("final")`
`(KE)_(i) +(PE)_(i)=(KE)_(f)+(PE)_(f)`
`(PE)_(i) =0, "since"PE` of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
`1/2m_(alpha)v_(alpha)^(2) + 0=0 + (kq_(1)q_(2))/(R)`
`rArr1/2m_(alpha)v_(alpha)^(2)=k(2exxze)/(R)rArrR=(4kze^(2))/(m_(alpha)v_(alpha)^(2)`
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
`R=R_(0)(A)^(1//3)`
where `R_(0) = 1.2xx10^(-15)m`
A= atomic mass number
R=radius of nucleus
Radius of a particular nucleus is calculated by the projection of `alpha-`particle from infinity at a particular speed. Let this radius be the true radius. If the radius calculation for the same nucleus is made by , `alpha-`particle with half of the earlier speed then the percentage error involved in the radius calculation is :
View SolutionOne of the major requirement in atomic structure is determination of location of electron inside an atom. The wave mechanical model establishes this in accordance with Heisenberg's uncertainity principle through the concept of orbitals. The orbitals are defined as that '3D' space in which probability of finding electron is maximum and are represented by wave functions `Psi_(n,l,m)` where n,l and m are quantum number. The variation of `Psi` is analysed in terms of polar coordinates and hence `Psi = f( r, 0 , phi)` where 'r' represents radius vector and 0 and `phi` represents angle `(/_)` Which the radius vector with x-axis respectively. The expressions of `Psi_(r,0, phi)` are often given in terms of `sigma` instead of r where `sigma=(2Zr)/(nalpha_(0))` and Z = atomic number and n= shell number.
Which of the following wave function cannot represent an atomic orbital of H-atom?
View SolutionOne of the major requirement in atomic structure is determination of location of electron inside an atom. The wave mechanical model establishes this in accordance with Heisenberg's uncertainity principle through the concept of orbitals. The orbitals are defined as that '3D' space in which probability of finding electron is maximum and are represented by wave functions `Psi_(n,l,m)` where n,l and m are quantum number. The variation of `Psi` is analysed in terms of polar coordinates and hence `Psi = f( r, 0 , phi)` where 'r' represents radius vector and 0 and `phi` represents angle `(/_)` Which the radius vector with x-axis respectively. The expressions of `Psi_(r,0, phi)` are often given in terms of `sigma` instead of r where `sigma=(2Zr)/(nalpha_(0))` and Z = atomic number and n= shell number.
Which of the following statement is incorrect with respect to `Psi_((r)) us.` r graph for H-atom?
View SolutionOne of the major requirement in atomic structure is determination of location of electron inside an atom. The wave mechanical model establishes this in accordance with Heisenberg's uncertainity principle through the concept of orbitals. The orbitals are defined as that '3D' space in which probability of finding electron is maximum and are represented by wave functions `Psi_(n,l,m)` where n,l and m are quantum number. The variation of `Psi` is analysed in terms of polar coordinates and hence `Psi = f( r, 0 , phi)` where 'r' represents radius vector and 0 and `phi` represents angle `(/_)` Which the radius vector with x-axis respectively. The expressions of `Psi_(r,0, phi)` are often given in terms of `sigma` instead of r where `sigma=(2Zr)/(nalpha_(0))` and Z = atomic number and n= shell number.
If an orbital is represented as:
`Psi_(r,0,phi)=2/3((1)/(3alpha_(0)))^(3//2).(sigma-1)(sigma^(2)-8sigma+12)`
`.sigma^(-sigma//2).cos0`
belong to which orbital?
View SolutionA hydrogen like species is in a spherical symmetrical orbital `S_(1)` having 3 radial nodes. It gets de-excited to another level `S_(2)` having no radial node. Energy of `S_(2)` orbital is 2.25 times energy of 1st Bohr robit of hydrogen atom.
Identify the species involvedgt
View SolutionA hydrogen like species is in a spherical symmetrical orbital `S_(1)` having 3 radial nodes. It gets de-excited to another level `S_(2)` having no radial node. Energy of `S_(2)` orbital is 2.25 times energy of 1st Bohr robit of hydrogen atom.
What is the orbital angular momentum quantum number of `S_(2)`?
View SolutionA hydrogen like species is in a spherical symmetrical orbital `S_(1)` having 3 radial nodes. It gets de-excited to another level `S_(2)` having no radial node. Energy of `S_(2)` orbital is 2.25 times energy of 1st Bohr robit of hydrogen atom. ltbr. What is the combined total number of nodes `("radial" +"angular) is" S_(1) and S_(2)?`
View SolutionLet us assume a different atomic model in which electron revolves around the nucleus (proton) at a separation r under the action of force which is different from electro-static force of attraction. The potential energy between an electron and the proton due to this force is given by `U=-k/(r^(4))` where k is a constant.
Find the radius of n th Bohr's orbit.
View SolutionLet us assume a different atomic model in which electron revolves around the nucleus (proton) at a separation r under the action of force which is different from electro-static force of attraction. The potential energy between an electron and the proton due to this force is given by `U=-k/(r^(4))` where k is a constant.
Find the radius of n th Bohr's orbit.
View SolutionLet us assume a different atomic model in which electron revolves around the nucleus (proton) at a separation r under the action of force which is different from electro-static force of attraction. The potential energy between an electron and the proton due to this force is given by `U=-k/(r^(4))` where k is a constant.
Find the radius of n th Bohr's orbit.
View Solutionthe only electron in the hydrogen atom resides under ordinary conditions in the first orbit. When energy is supplied the electron moves to higher energy orbit depending on the amount of energy absorbed. It emits energy. Lyman series is formed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns to second. Similarly, Paschen, Breakett and Pfund series are formed when electron returns to the third, fourth and fifth orbits from higher energy orbits respectively (as shown in figure).

Maximum number of different lines produced when electron jump from nth level to ground level is equal to
`(n(n-1))/(2).`
For example in the case of `n=4,` number of lines produced is `6.(4to3,4to2,4to1,3to2,3to1,2to1).`When an electron returns from `n_(2) "to"n_(1)` state, the number of different
lines in the spectrum will be equal to `((n_(2)-n_(1))(n_(2)-n_(1)+1))/(2)`
If the electron comes back from energy level having energy `E_(2)` to energy level having energy `E_(1),` then the difference may be expressed in terms of energy of photon as:
`E_(2)-E_(1)=DeltaE,lambda=(hc)/(DeltaE),DeltaE=hv(v-"frequency")`
Since h and c are constants `DeltaE` corresponds to definite energy: thus each transition from one energy level to another will produce a light of definite wavelength. This is actually observed as a line in the spectrum of hydrogen atom.
Wave number of line is given by the formula:
`barv=RZ^(2)((1)/(n_(1)^(2))-(1)/(n_(2)^(2)))`
where R is a Rydberg constant `(R=1.1xx10^(7)m^(-1)).`
(i) First line of a series : It is called line of longest wavelength of line of smallest energy'.
(ii) Series limit or last line of a series : It is the line of shortest wavelength or line of highest energy.
Last line of breakett series for H-atom has wavelength `lambda_(1)"Å"` and 2nd line of Lyman series has wavelength `lambda_(2)"Å"`then:
View Solutionthe only electron in the hydrogen atom resides under ordinary conditions in the first orbit. When energy is supplied the electron moves to higher energy orbit depending on the amount of energy absorbed. It emits energy. Lyman series is formed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns to second. Similarly, Paschen, Breakett and Pfund series are formed when electron returns to the third, fourth and fifth orbits from higher energy orbits respectively (as shown in figure).
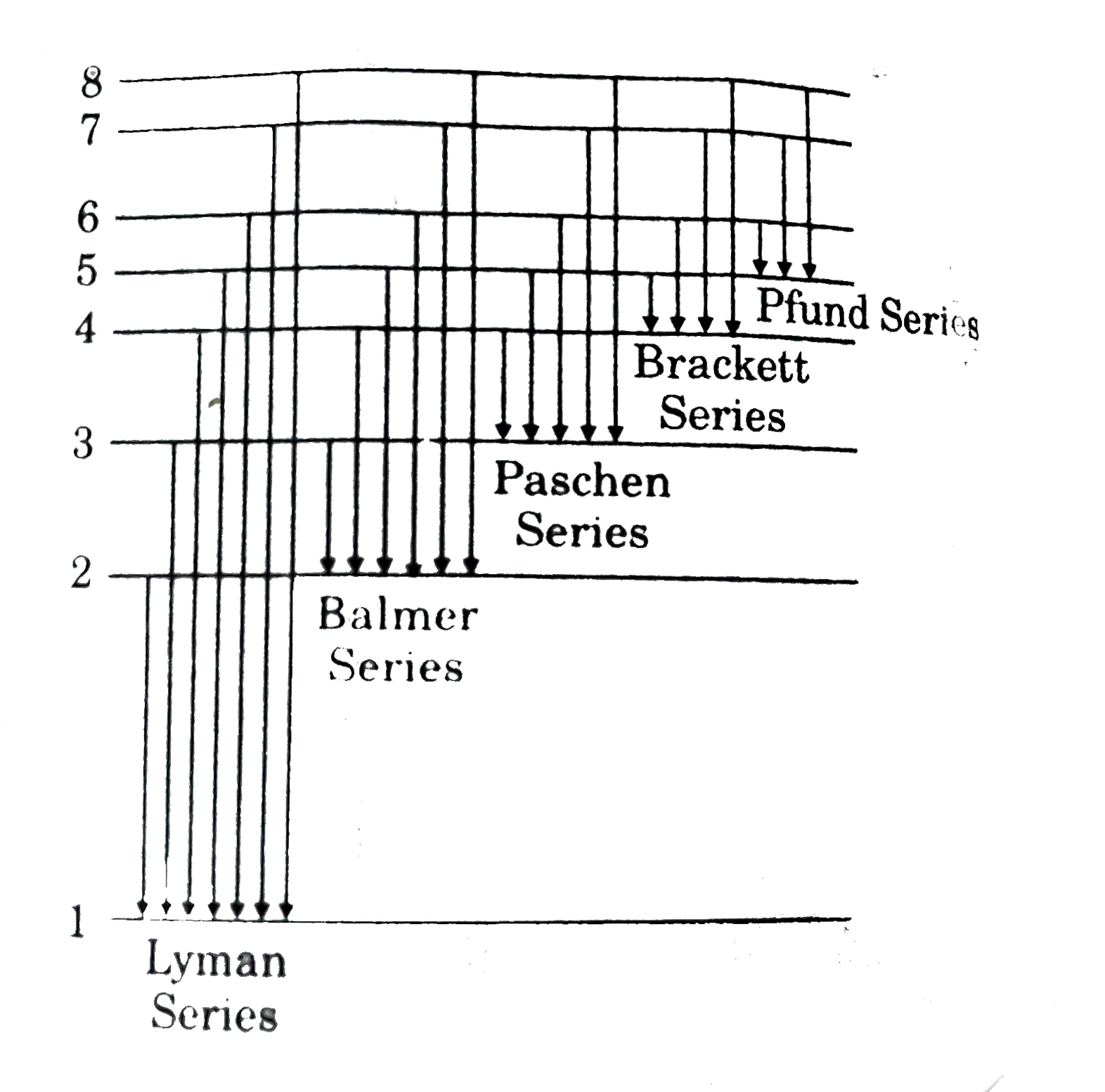
Maximum number of different lines produced when electron jump from nth level to ground level is equal to
`(n(n-1))/(2).`
For example in the case of `n=4,` number of lines produced is `6.(4to3,4to2,4to1,3to2,3to1,2to1).`When an electron returns from `n_(2) "to"n_(1)` state, the number of different
lines in the spectrum will be equal to `((n_(2)-n_(1))(n_(2)-n_(1)+1))/(2)`
If the electron comes back from energy level having energy `E_(2)` to energy level having energy `E_(1),` then the difference may be expressed in terms of energy of photon as:
`E_(2)-E_(1)=DeltaE,lambda=(hc)/(DeltaE),DeltaE=hv(v-"frequency")`
Since h and c are constants `DeltaE` corresponds to definite energy: thus each transition from one energy level to another will produce a light of definite wavelength. This is actually observed as a line in the spectrum of hydrogen atom.
Wave number of line is given by the formula:
`barv=RZ^(2)((1)/(n_(1)^(2))-(1)/(n_(2)^(2)))`
where R is a Rydberg constant `(R=1.1xx10^(7)m^(-1)).`
(i) First line of a series : It is called line of longest wavelength of line of smallest energy'.
(ii) Series limit or last line of a series : It is the line of shortest wavelength or line of highest energy.
Consider the following statements
(i) Spectral lines of `He^(+)`ion belonging to Balmer series are not in visible range.
(ii) In the Balmer series of H-atom maximum lines are in ultraviolet ragion.
(iii) 2nd line of Lyman series of `He^(+)` ion has energy `48.35 eV`
The above statement (i), (ii), (iii) respectively are`(T=True, F=False):`
View Solutionthe only electron in the hydrogen atom resides under ordinary conditions in the first orbit. When energy is supplied the electron moves to higher energy orbit depending on the amount of energy absorbed. It emits energy. Lyman series is formed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns to second. Similarly, Paschen, Breakett and Pfund series are formed when electron returns to the third, fourth and fifth orbits from higher energy orbits respectively (as shown in figure).
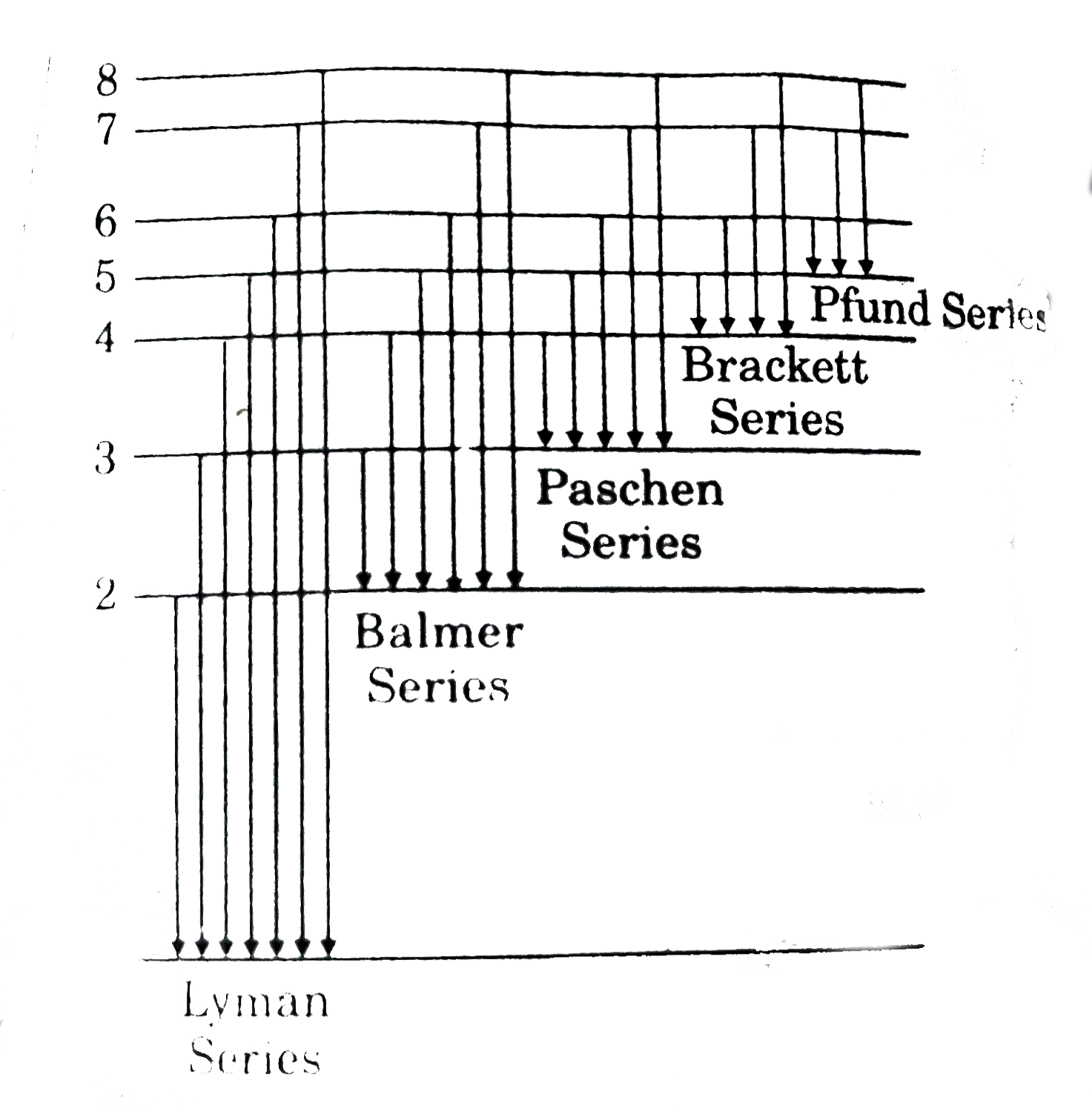
Maximum number of different lines produced when electron jump from nth level to ground level is equal to
`(n(n-1))/(2).`
For example in the case of `n=4,` number of lines produced is `6.(4to3,4to2,4to1,3to2,3to1,2to1).`When an electron returns from `n_(2) "to"n_(1)` state, the number of different
lines in the spectrum will be equal to `((n_(2)-n_(1))(n_(2)-n_(1)+1))/(2)`
If the electron comes back from energy level having energy `E_(2)` to energy level having energy `E_(1),` then the difference may be expressed in terms of energy of photon as:
`E_(2)-E_(1)=DeltaE,lambda=(hc)/(DeltaE),DeltaE=hv(v-"frequency")`
Since h and c are constants `DeltaE` corresponds to definite energy: thus each transition from one energy level to another will produce a light of definite wavelength. This is actually observed as a line in the spectrum of hydrogen atom.
Wave number of line is given by the formula:
`barv=RZ^(2)((1)/(n_(1)^(2))-(1)/(n_(2)^(2)))`
where R is a Rydberg constant `(R=1.1xx10^(7)m^(-1)).`
(i) First line of a series : It is called line of longest wavelength of line of smallest energy'.
(ii) Series limit or last line of a series : It is the line of shortest wavelength or line of highest energy.
wave number of the first line of Paschen series in `Be^(3+)` ion is :
View Solutionde Broglie proposed dual nature for electron by putting his famous equation `lambda = (h)/(mv).` Later on, Heisenberg proposed uncertainty principle as `deltapDeltax ge (h)/(4pi).` On the contrary,
Particle nature of electron was established on the basis of photoelectric effect. When a photon strikes the metal surface it gives up its energy to the electron. Part of this energy (say W) is used by the electrons to escape from the metal and the remaining energy imparts kinetic energy `(1//2 mv^(2))` to the ejected photoelectron. The potential applied on the surface to reduce the velocity of photoelectron to zero is known as stopping potential .
When a beam of photons of a particular energy was incident on a surface of a particular pure metal having work function =(40 eV), some emitted photoelectrons had stopping potential equal to 22 V. some had 12V and rest had lower values. Calculate the wavelength of incident photons assuming that at least one photoelectron is ejected with maximum possible kinetic energy :
View Solutionde Broglie proposed dual nature for electron by putting his famous equation `lambda = (h)/(mv).` Later on, Heisenberg proposed uncertainty principle as `deltapDeltax ge (h)/(4pi).` On the contrary,
Particle nature of electron was established on the basis of photoelectric effect. When a photon strikes the metal surface it gives up its energy to the electron. Part of this energy (say W) is used by the electrons to escape from the metal and the remaining energy imparts kinetic energy `(1//2 mv^(2))` to the ejected photoelectron. The potential applied on the surface to reduce the velocity of photoelectron to zero is known as stopping potential .
The circumference of third orbit of a single electron species is 3 nm. What may be the approximate wavelength of the photon required to just ionize electron from this orbit?
View SolutionExcited atoms emit radiations consisting of only certain discrete frequencise or wavelengths. In spectroscopy it is often more convenient to use freuquencies and wave numbers are proportional ot energy and spectroscopy involves transitions between different energy levels . The line spectrum shown by a single electron excited atom (a finger print of an atom) can be given as
`1/(lambda)=barvR_(H).Z^(2)[(1)/(n_(1)^(2))-(1)/(n_(2)^(2))]`
where Z is atomic number of single electron atom and `n_(1),n_(2)` are integers and if `n_(2)gt n_(1),` then emission spectrum is noticed and if `n_(2)ltn_(1),` then absorption spectrum is noticed.
Every line in spectrum can be represented as a difference of two terms `(R_(H)Z^(2))/(n_(1)^(2)) "and"(R_(H)Z^(2))/(n_(2)^(2)).`
The ratio of wavelength for II line fo Balmer series and I line of Lyman series for H-like species is :
View SolutionExcited atoms emit radiations consisting of only certain discrete frequencise or wavelengths. In spectroscopy it is often more convenient to use freuquencies and wave numbers are proportional ot energy and spectroscopy involves transitions between different energy levels . The line spectrum shown by a single electron excited atom (a finger print of an atom) can be given as
`1/(lambda)=barvR_(H).Z^(2)[(1)/(n_(1)^(2))-(1)/(n_(2)^(2))]`
where Z is atomic number of single electron atom and `n_(1),n_(2)` are integers and if `n_(2)gt n_(1),` then emission spectrum is noticed and if `n_(2)ltn_(1),` then absorption spectrum is noticed.
Every line in spectrum can be represented as a difference of two terms `(R_(H)Z^(2))/(n_(1)^(2)) "and"(R_(H)Z^(2))/(n_(2)^(2)).`
H-atoms in ground state (13.6 eV) are excited by monochromatic radiations of photon of energy 12.09 eV. The number of different spectral lines emitted in H-atoms will be:
View SolutionIn an atom when an electron jumps from higher energy level to lower energy level it amits energy in form of elecromagnetic radiations. When these elecromagnetic radiations are passed through a prism and received on a photographic film some lines are observed on that film and those lines are called spectral lines.
For hydrogen like species when jump takes from any excited state to ground state `(n=1)`, line produced in that case is called a Lyman series line.
If transition occurs from 3rd or above level to second level then corresponding lines produced are called Balmer lines. Similarly, for next level it is called Paschen series line.
The wavelength of photon corresponding ot second least energy of Lyman series in H-atom is :
View SolutionIn an atom when an electron jumps from higher energy level to lower energy level it amits energy in form of elecromagnetic radiations. When these elecromagnetic radiations are passed through a prism and received on a photographic film some lines are observed on that film and those lines are called spectral lines.
For hydrogen like species when jump takes from any excited state to ground state `(n=1)`, line produced in that case is called a Lyman series line.
If transition occurs from 3rd or above level to second level then corresponding lines produced are called Balmer lines. Similarly, for next level it is called Paschen series line.
If there are 3 atoms of a hydrogen like species one in 2nd one in 3rd and one in 4th excited state, then how many maximum total different Balmer and Paschen lines can be produced ?
View SolutionFrom hydrogen gas discharge tube, light is emitted. Emitted light is used to emit electron from sodium metal of work function `phi= 1.82 eV`
If the fastest photoelectron has KE of 0.73 eV, the wavelength of incident radiation on the sodium metal is :
View SolutionFrom hydrogen gas discharge tube, light is emitted. Emitted light is used to emit electron from sodium metal of work function `phi= 1.82 eV`
the transition in hydrogen atom takes place from:
View SolutionIn a H-like species there are two energy levels A and B above the ground state having principal quantum numbers of `n_(1) "and"n_(2)` respectively. A sample of this H-like species has all atoms`//`ions in excited levels A or B only and none in any other energy level. Energy of level B is greater than that of level A and a total of 15 different lines are emitted from this sample on returning to ground state out of which 6 lines are emitted due to electronic transitions between the level `n_(1)"and"n_(2)` only. Also energy difference between levels `n_(2) "and"n_(1), E_(n_2)-E_(n_2)=4.53 eV`
The correct option is :
View SolutionIn a H-like species there are two energy levels A and B above the ground state having principal quantum numbers of `n_(1) "and"n_(2)` respectively. A sample of this H-like species has all atoms`//`ions in excited levels A or B only and none in any other energy level. Energy of level B is greater than that of level A and a total of 15 different lines are emitted from this sample on returning to ground state out of which 6 lines are emitted due to electronic transitions between the level `n_(1)"and"n_(2)` only. Also energy difference between levels `n_(2) "and"n_(1), E_(n_2)-E_(n_2)=4.53 eV`
Calculate minimum wavelength of the above transition:
View SolutionThe following text gives a qualitative idea about Rutherford's `alpha-` particle scattering experiment.

Applying some trigonometry and calculus, Rutherford got the following equation:
`cot ((0)/(2)) = (Kxx(KE))/(Ze^(2))xxb`
`"where", K= "constant" =((1)/(9xx10))(c^(2))/(N-m^(2))`
KE = initial kinetic energy of `alpha-`particle,
`e=1.6xx10^(-19)C`
Identify the incorrect statement.
View SolutionThe following text gives a qualitative idea about Rutherford's `alpha-` particle scattering experiment.

Applying some trigonometry and calculus, Rutherford got the following equation:
`cot ((0)/(2)) = (Kxx(KE))/(Ze^(2))xxb`
`"where", K= "constant" =((1)/(9xx10))(c^(2))/(N-m^(2))`
KE = initial kinetic energy of `alpha-`particle,
`e=1.6xx10^(-19)C`
In an experment with gold nucleus (assume Z=80) with impact parameter equal to `10^(-4)m` the scattering angle was found to be `90^(@),` What should be the initial KE of `alpha-`particle?
View SolutionIn three dimension wave function may be expressed in spherical co-ordinate system `(r,0,phi),r=`distance of electron from the nucleus
0= Angle from 'z' axis varying from 0 to `pi`
`phi =` Angle from 'x' axis …… 0 to `2pi` ltbr. `Psi` may be represented as
`Psi (r,0,phi)=R (r) .A(0, phi)`
The R(r) is detemind by 'n' and 'l'. The A `(0,phi)` is determined by 'l' and 'm'.
Which of the following is R(r) part of '3p' atomic orbital of hydrogen atom `["Given" alpha_(0) = 0.529 "Å"]`?
View SolutionIn three dimension wave function may be expressed in spherical co-ordinate system `(r,0,phi),r=`distance of electron from the nucleus
0= Angle from 'z' axis varying from 0 to `pi`
`phi =` Angle from 'x' axis …… 0 to `2pi` ltbr. `Psi` may be represented as
`Psi (r,0,phi)=R (r) .A(0, phi)`
The R(r) is detemind by 'n' and 'l'. The A `(0,phi)` is determined by 'l' and 'm'.
Angular part of 'H' atom wave equation `A(0,phi)= (1)/sqrt(4pi).`Hence , atomic orbital is:
View SolutionDuring one of its ambitious project ''ISRP" gathered information through its stallites for a planet in another galaxy. As far as structure of atoms is considered , it is very similar to the structure of an atom in our planet except that
energy of an orbit in which electron resides is `(E_(n))=(45xxZ)/(n=1) eV//"atom".`
Calculate wavelength `("in""Å")` of photon emitted when electron makes transition from 7th excited state to 1st excited state in H-atom of that planet:
View SolutionDuring one of its ambitious project ''ISRP" gathered information through its stallites for a planet in another galaxy. As far as structure of atoms is considered , it is very similar to the structure of an atom in our planet except that
energy of an orbit in which electron resides is `(E_(n))=(45xxZ)/(n=1) eV//"atom".`
If photon of wavelength 7nm strikes on an atom of hydrogen on that planet, then wavelength of ejected electron will be approximately:
View SolutionDuring one of its ambitious project ''ISRP" gathered information through its stallites for a planet in another galaxy. As far as structure of atoms is considered , it is very similar to the structure of an atom in our planet except that
energy of an orbit in which electron resides is `(E_(n))=(45xxZ)/(n=1) eV//"atom".`
If collection of H-atom and `He^(+)` ion makes transition from 2nd orbit and 5th orbit respectively, then total different spectral lines emitted will be :
View SolutionA H-like species `Be^(3+)` is in a spherically symmetric state `S_(1)` with two radial nodes. Upon absorbing light the ion undergoes transition to a state `S_(2)`. The state `S_(2)` has one radial node and its energy is equal to the ground state energy of the H-atom.
The state`S_(1) is :
View SolutionA H-like species `Be^(3+)` is in a spherically symmetric state `S_(1)` with two radial nodes. Upon absorbing light the ion undergoes transition to a state `S_(2)`. The state `S_(2)` has one radial node and its energy is equal to the ground state energy of the H-atom.
Energy of state `S_(1)` in units of `He^(+)` ground state energy is :
View SolutionA H-like species `Be^(3+)` is in a spherically symmetric state `S_(1)` with two radial nodes. Upon absorbing light the ion undergoes transition to a state `S_(2)`. The state `S_(2)` has one radial node and its energy is equal to the ground state energy of the H-atom.
The orbital angular momentum of hte state `S_(2)` is :
View SolutionThe French physicist Louis de Broglie in 1924 postulated that matter like radiation , should exhibit a dual behaviour. He proposed the following relationship between the wavelength `.lambda` of a material particle,its linear momentum P and Planck constant h.
`lambda=(h)/(p)=(h)/(mv)`
The de Broglie relaion that the wavelength of a particle should decrease as its velocity increases. It also implies that for a given velocity heavier particles should have shorter wavelength than lighter particles.The waves or de Broglie waves. These waves differ from the electromagnetic waves as they:
(i) have lower velocities
(ii) have no electrical and magnetic fields and
(iii) are not emitted by the particle under consideration.
The expermental confirmation of the de Broglie relation was obtained when Davission and Germer in 1927, observed. As diffraction is a characteristic property of waves, hence the beam of electrons behave as a wave as proposed by de Broglie.
Werner Heisenberg considered the limits of how precisely we can measure properties of an electron or other microscopic particle like electron . He determined that there is a fundamental limit of how closely we can measure both position and momentum. The more accurately we can determine its position. The converse is also true. This is summed up in what we now call the ''Heisenberg uncertainty principle'' : It is impossible to determine simultaneously and precisely both the momentum and position of a particle. The product of uncertainty in the position, `Deltax` and the uncertainty in the momentum `Delta(mv)` must be greater than or equal to `(h)/(4pi), i.e.,`
`Deltax Delta(mv)ge(h)/(4pi)`
The correct order of wavelength of Hydrogen `(._(1)H^(1))` Deuterium `(._(1)H^(2))` and Tritium `(._(1)H^(3))` moving with same kinetic energy is :
View SolutionThe French physicist Louis de Broglie in 1924 postulated that matter like radiation , should exhibit a dual behaviour. He proposed the following relationship between the wavelength `.lambda` of a material particle,its linear momentum P and Planck constant h.
`lambda=(h)/(p)=(h)/(mv)`
The de Broglie relaion that the wavelength of a particle should decrease as its velocity increases. It also implies that for a given velocity heavier particles should have shorter wavelength than lighter particles.The waves or de Broglie waves. These waves differ from the electromagnetic waves as they:
(i) have lower velocities
(ii) have no electrical and magnetic fields and
(iii) are not emitted by the particle under consideration.
The expermental confirmation of the de Broglie relation was obtained when Davission and Germer in 1927, observed. As diffraction is a characteristic property of waves, hence the beam of electrons behave as a wave as proposed by de Broglie.
Werner Heisenberg considered the limits of how precisely we can measure properties of an electron or other microscopic particle like electron . He determined that there is a fundamental limit of how closely we can measure both position and momentum. The more accurately we can determine its position. The converse is also true. This is summed up in what we now call the ''Heisenberg uncertainty principle'' : It is impossible to determine simultaneously and precisely both the momentum and position of a particle. The product of uncertainty in the position, `Deltax` and the uncertainty in the momentum `Delta(mv)` must be greater than or equal to `(h)/(4pi), i.e.,`
`Deltax Delta(mv)ge(h)/(4pi)`
The transition so that the de Broglie wavelength of electron becomes 3 times of its initial value in `He^(+)` ion will be :
View SolutionThe French physicist Louis de Broglie in 1924 postulated that matter like radiation , should exhibit a dual behaviour. He proposed the following relationship between the wavelength `.lambda` of a material particle,its linear momentum P and Planck constant h.
`lambda=(h)/(p)=(h)/(mv)`
The de Broglie relaion that the wavelength of a particle should decrease as its velocity increases. It also implies that for a given velocity heavier particles should have shorter wavelength than lighter particles.The waves or de Broglie waves. These waves differ from the electromagnetic waves as they:
(i) have lower velocities
(ii) have no electrical and magnetic fields and
(iii) are not emitted by the particle under consideration.
The expermental confirmation of the de Broglie relation was obtained when Davission and Germer in 1927, observed. As diffraction is a characteristic property of waves, hence the beam of electrons behave as a wave as proposed by de Broglie.
Werner Heisenberg considered the limits of how precisely we can measure properties of an electron or other microscopic particle like electron . He determined that there is a fundamental limit of how closely we can measure both position and momentum. The more accurately we can determine its position. The converse is also true. This is summed up in what we now call the ''Heisenberg uncertainty principle'' : It is impossible to determine simultaneously and precisely both the momentum and position of a particle. The product of uncertainty in the position, `Deltax` and the uncertainty in the momentum `Delta(mv)` must be greater than or equal to `(h)/(4pi), i.e.,`
`Deltax Delta(mv)ge(h)/(4pi)`
If the uncertainty in velocity and posititon is same then the uncertainty in momentum will be :
View Solution
Comprehesion Type questions and complete solutions for chapter ATOMIC STRUCTURE of GRB CHEMISTRY (HINGLISH) of Class 11