Complete Solutions to Comprehension type Queston of chapter MOTION IN A STRAIGHT LINE of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN A STRAIGHT LINE |
| GRB PUBLICATION | Comprehension type Queston |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
A particle is moving along X-axis under a force such that its position -time graph is as shown in figure.

As the particle passes position (1):
View SolutionA particle is moving along X-axis under a force such that its position -time graph is as shown in figure.

As the particle passes position (2):
View SolutionA particle is moving along X-axis under a force such that its position -time graph is as shown in figure.

As the particle passes position (3) :
View SolutionA particle is moving along X-axis under a force such that its position -time graph is as shown in figure.

As the particle passes position (5) :
View SolutionA particle is moving along X-axis under a force such that its position -time graph is as shown in figure.

As the particle passes position (5) :
View SolutionA particle is moving along X-axis under a force such that its position -time graph is as shown in figure.

As the particle passes position (6) :
View SolutionA person standing on the roof of a building throws a ball vertically upward at an instant `t = 0`. The ball leaves his hand with an upward speed 20 m/s and it is then in free fall. The ball rises to a certain height and then moves down. On its way down, the ball just misses to hit the roof of the building and keeps falling towards the earth. the ball hits earth at `t = 5`sec. considering that (i) the vertically upward direction is the positive Y-direction (ii) the position of ball at `t = 0` is the origin (iii) the ball does not rebound and comes to rest at the same place where it hits earth and (iv) air resistance is negligible. (Take `g = 10 m//s^(2)`)
Maximum displacement of the ball from the initial position is :
View SolutionA person standing on the roof of a building throws a ball vertically upward at an instant `t = 0`. The ball leaves his hand with an upward speed 20 m/s and it is then in free fall. The ball rises to a certain height and then moves down. On its way down, the ball just misses to hit the roof of the building and keeps falling towards the earth. the ball hits earth at `t = 5`sec. considering that (i) the vertically upward direction is the positive Y-direction (ii) the position of ball at `t = 0` is the origin (iii) the ball does not rebound and comes to rest at the same place where it hits earth and (iv) air resistance is negligible. (Take `g = 10 m//s^(2)`)
Average velocity of the ball from `t = 0` to `t = 5` sec
View SolutionA person standing on the roof of a building throws a ball vertically upward at an instant `t = 0`. The ball leaves his hand with an upward speed 20 m/s and it is then in free fall. The ball rises to a certain height and then moves down. On its way down, the ball just misses to hit the roof of the building and keeps falling towards the earth. the ball hits earth at `t = 5`sec. considering that (i) the vertically upward direction is the positive Y-direction (ii) the position of ball at `t = 0` is the origin (iii) the ball does not rebound and comes to rest at the same place where it hits earth and (iv) air resistance is negligible. (Take `g = 10 m//s^(2)`)
Position -time graph for the given motion of the ball is :
View SolutionA person standing on the roof of a building throws a ball vertically upward at an instant `t = 0`. The ball leaves his hand with an upward speed 20 m/s and it is then in free fall. The ball rises to a certain height and then moves down. On its way down, the ball just misses to hit the roof of the building and keeps falling towards the earth. the ball hits earth at `t = 5`sec. considering that (i) the vertically upward direction is the positive Y-direction (ii) the position of ball at `t = 0` is the origin (iii) the ball does not rebound and comes to rest at the same place where it hits earth and (iv) air resistance is negligible. (Take `g = 10 m//s^(2)`)
Velocity of the ball will vary with time as:
View SolutionA person standing on the roof of a building throws a ball vertically upward at an instant `t = 0`. The ball leaves his hand with an upward speed 20 m/s and it is then in free fall. The ball rises to a certain height and then moves down. On its way down, the ball just misses to hit the roof of the building and keeps falling towards the earth. the ball hits earth at `t = 5`sec. considering that (i) the vertically upward direction is the positive Y-direction (ii) the position of ball at `t = 0` is the origin (iii) the ball does not rebound and comes to rest at the same place where it hits earth and (iv) air resistance is negligible. (Take `g = 10 m//s^(2)`)
Acceleration of the ball will vary with time as:
View SolutionConsider a particle moving along x-axis. Its distance from origin O is described by the co-ordinate x which varies with time. At a time `t_(1)`, the particle is at point P, where its co-ordinate is `x_(1)` and at time `t_(2)`, the particle is at point Q, where its co-ordinate is `x_(2)`. The displacement during the time interval from `t_(1)` to `t_(2)` is the vector from P to Q, the x-component of this vector is `(x_(2) - x_(1))` and all other components are zero.
It is convenient to represent the quantity `x_(2) - x_(1)` the change in x by means of a notation `Delta`, thus `Delta x = x_(2) - x_(1)` and `Delta t = t_(2) - t_(1)`.
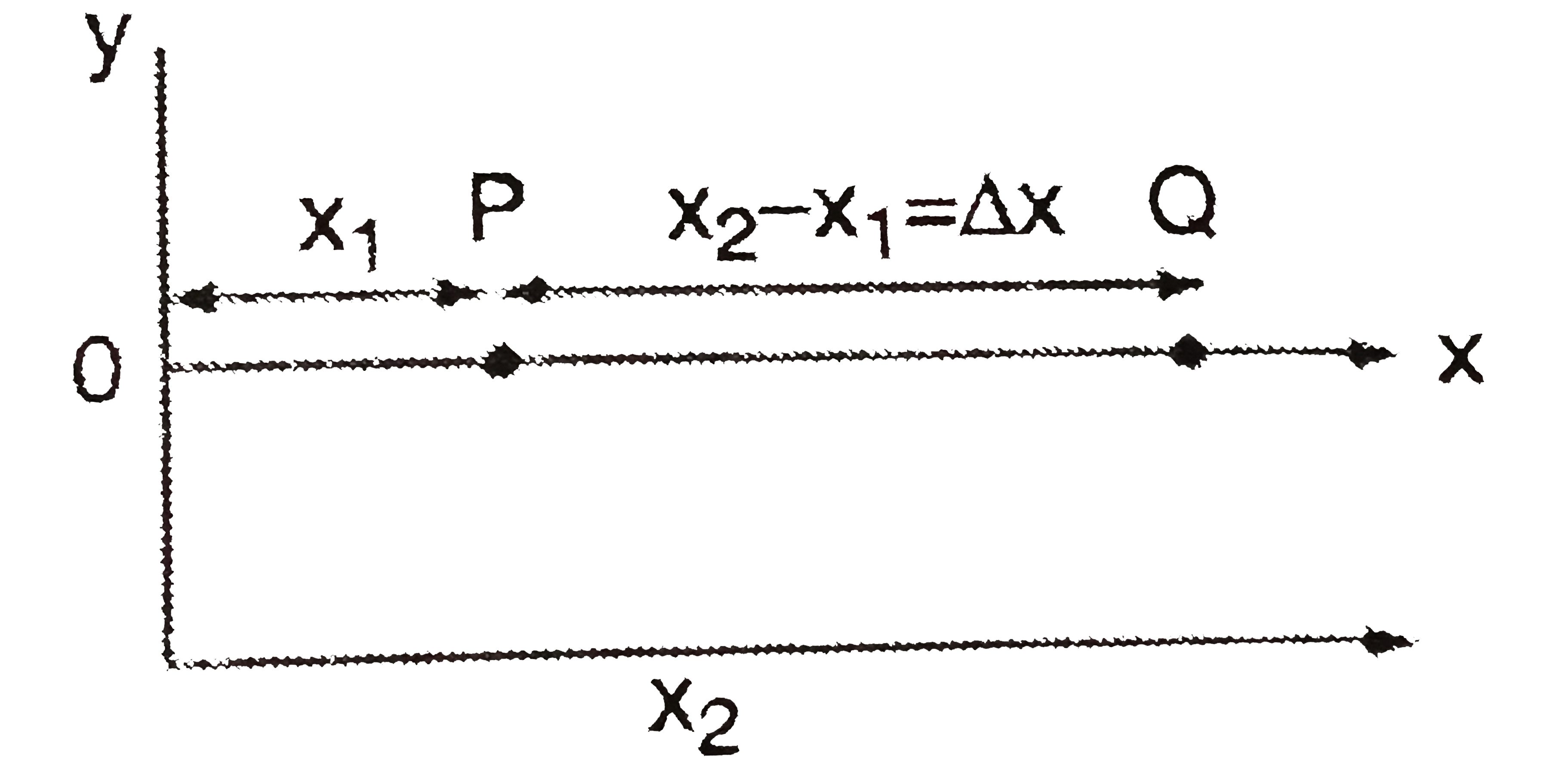
The average velocity `bar(V) = (x_(2) - x_(1))/(t_(2) - t_(1)) = (Delta x)/(Delta t)`
A particle moves half the time of its journey with `u`. The rest of the half time it moves with two velocities `v_(1)` and `v_(2)` such that half the distance it covers with `v_(1)` and the other half with `v_(2)`. The net average velocity is: (Assume straight line motion)
View SolutionConsider a particle moving along x-axis. Its distance from origin O is described by the co-ordinate x which varies with time. At a time `t_(1)`, the particle is at point P, where its co-ordinate is `x_(1)` and at time `t_(2)`, the particle is at point Q, where its co-ordinate is `x_(2)`. The displacement during the time interval from `t_(1)` to `t_(2)` is the vector from P to Q, the x-component of this vector is `(x_(2) - x_(1))` and all other components are zero.
It is convenient to represent the quantity `x_(2) - x_(1)` the change in x by means of a notation `Delta`, thus `Delta x = x_(2) - x_(1)` and `Delta t = t_(2) - t_(1)`.
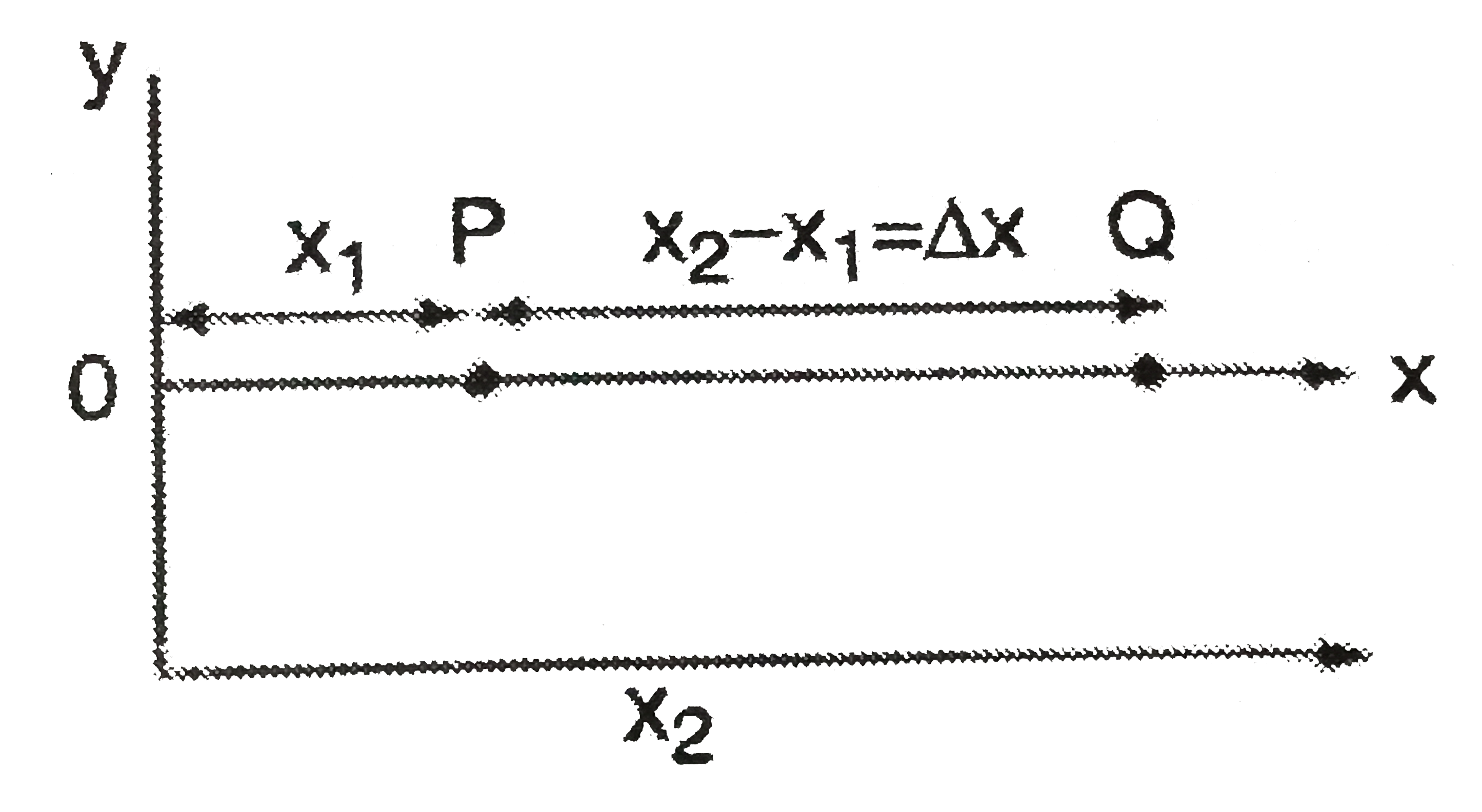
The average velocity `bar(V) = (x_(2) - x_(1))/(t_(2) - t_(1)) = (Delta x)/(Delta t)`
A particle moves according to the equation `x = t^(2) + 3t + 4`. The average velocity in the first 5 s is:
View SolutionConsider a particle moving along x-axis. Its distance from origin O is described by the co-ordinate x which varies with time. At a time `t_(1)`, the particle is at point P, where its co-ordinate is `x_(1)` and at time `t_(2)`, the particle is at point Q, where its co-ordinate is `x_(2)`. The displacement during the time interval from `t_(1)` to `t_(2)` is the vector from P to Q, the x-component of this vector is `(x_(2) - x_(1))` and all other components are zero.
It is convenient to represent the quantity `x_(2) - x_(1)` the change in x by means of a notation `Delta`, thus `Delta x = x_(2) - x_(1)` and `Delta t = t_(2) - t_(1)`.

The average velocity `bar(V) = (x_(2) - x_(1))/(t_(2) - t_(1)) = (Delta x)/(Delta t)`
The resistive force suffered by a motor boat is proportional to `v^(2)`, where `v` is instantaneous velocity. The engine was shut down when the velocity of the boat was `v_(0)`. Find the average velocity at any time `t`.
View Solution
Comprehension type Queston questions and complete solutions for chapter MOTION IN A STRAIGHT LINE of GR BATHLA & SONS PHYSICS (HINGLISH) of Class 11