Complete Solutions to worked out Examples of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| HC VERMA | worked out Examples |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
The equation of a particle executing simple harmonic motion is `x=(5m)sin[(pis^-1)t+pi/3].` Write down the amplitude time period and maximum speed. Also find the velocity at t=1s.
View SolutionA block of mass 5 kg executes simple harmonic motion under the restoring force of a spring. The amplitude and the time period of the motion are 0.1 m and 3.14 s respectively. Find the maximum force exerted by the spring on the block.
View SolutionA particle executing simple harmonic motion has angular frequency `6.28 s^(-1)` and amplitude `10 cm`. Find `(a)` the time period, `(b)` the maximum speed, `(c)` the maximum acceleration.
View SolutionA particle executes a simple harmonic motion of time period T. Find the time taken by the particle to go directly from its mean position to half the amplitude.
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA particle suspended from a vertical spring oscillates 10 times per second. At the highest point of oscillation the spring becomes unstretched. A. Find the maximum speed of the block. B. Find the speed when the spring is stretched by 0.20 cm. Take `g=pi^2ms^-2`
View SolutionThe pulley shown in figure has a moment of inertias I about its axis and mass m. find the time period of vertical oscillation of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

View SolutionFind the blanks:

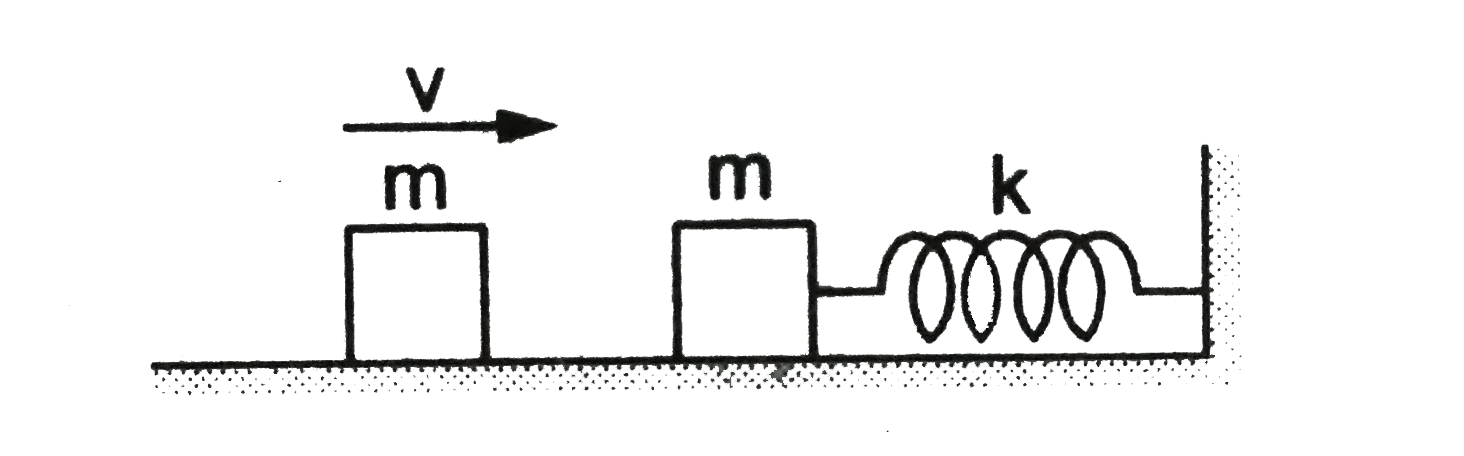
View SolutionThe left block in filgure collides inelastically with the right block and sticks to it. Find the amplitude of the resulting simple harmonic motion.
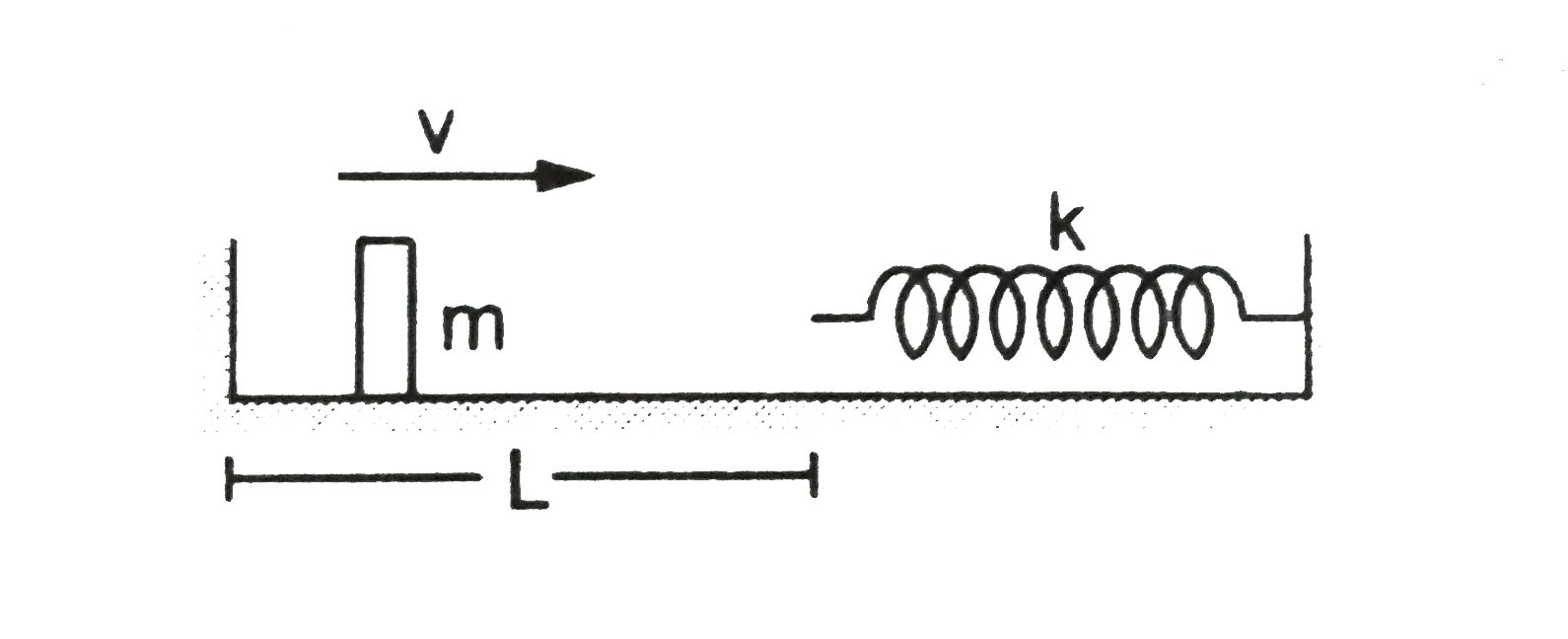
View SolutionDescribe the motion of the mass m shown in figure. The walls and the block are elastic.
View SolutionA block of mass m is suspended from the ceiling of a stationary standig elevator through a spring of spring constant k. Suddenly, the cable breaks and the elevator starts falling freely. Show that the bklock now executes a simple harmonic motion of amplitude `mg/k` in the elevator
View SolutionThe spring as shown in figure is kept in a stretched position with extension `Xo` when the system is released. Assuming the horizontal surface to be frictionless, the frequency of oscillation is

View SolutionAssume that as narrow tunnel is dug between two diametrically opposite points of the earth. Treat the earth as a solid sphere of uniform density. Show that if a particle is released in this tunnel, it will execute a simple harmonic motion. Calculate the time period of this motion.
View SolutionA simple pendulum of length 40 cm oscillates with an angular amplitude of 0.04 rad. Find a. the time period b. the linear amplitude of the bob.
View SolutionA simple pendulum having a bob of mass m under goes small oscillations with amplitude `theta_0` Find the tension in the string as a function of the angle made by the string with the vertical. When in this tension maximum, and when is it minimum?
View SolutionA simple pendulum is taken at a place where its separation from the earth's surface is equal to the radius of the earth. Calculate the time period of small oscillation if the length of the string is `1.0m`. Take `g = pi^(2) m//s^(2)` at the surface of the earth.
View SolutionA simple pendulum is suspended from the ceiling a car accelerating uniformly on a horizontal road. If the acceleration is `a_0` and the length of the pendulum is l, find the time period of small oscillations about the mean position.
View SolutionA uniform meter stick is suspended through a small pin hole at the 10 cm mark. Find the time period of small oscillation about the point of suspension.
View SolutionThe moment of inertia of the disc used in a torsional pendulum about the suspension wire is `0.2kg-m^2`. It oscillates with a period of 2s. Asnother disc is placed over the first one and time period of the system becomes 2.5s. Find the moment of inertia of the second disc about the wire.

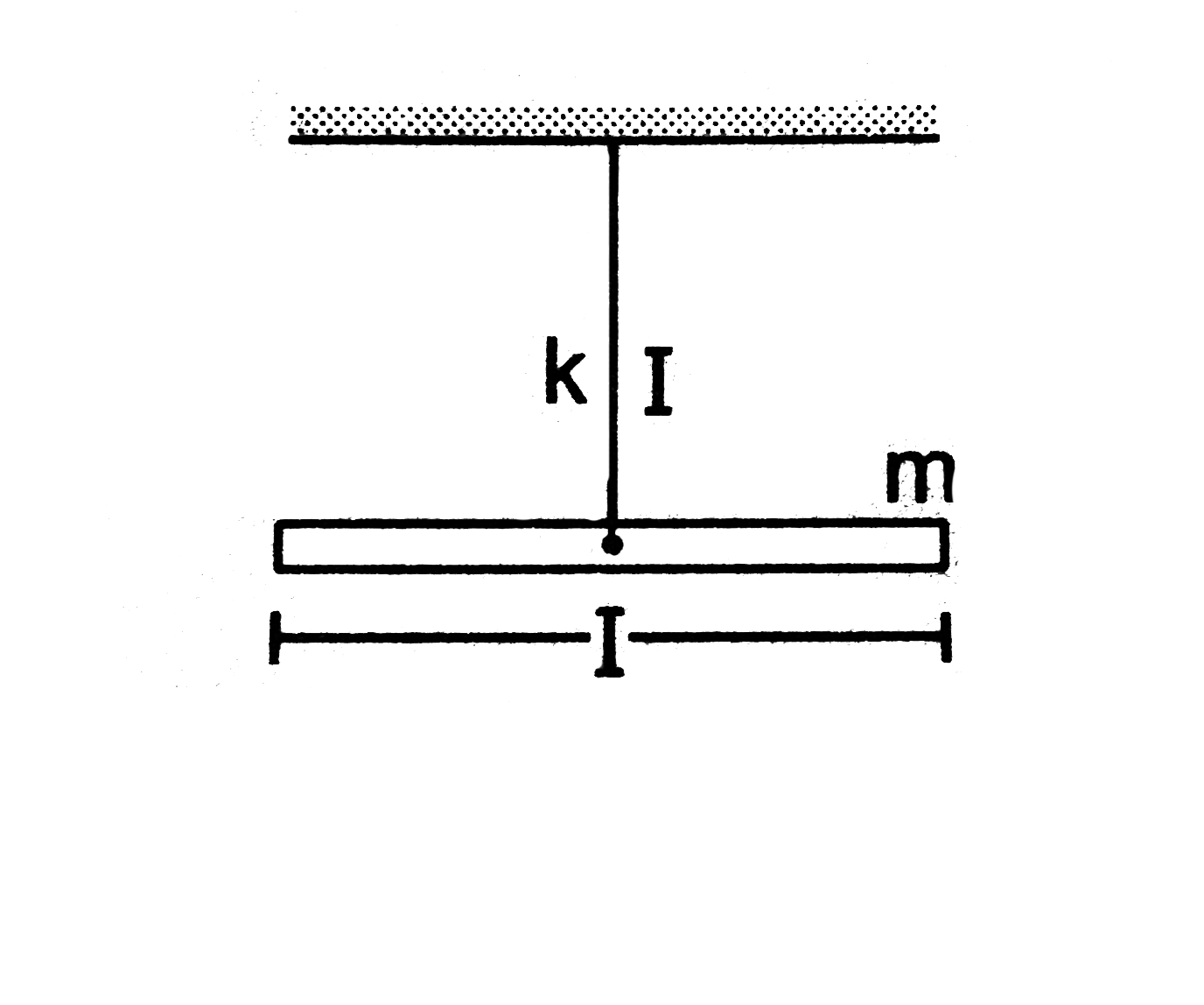
View SolutionA uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time period of the system makes small oscillations in the vertical plane about the suspension point .
View SolutionA particle is subjected to two simple harmonic motions
`x_1=A_1 sinomegat`
`and x_2=A_2sin(omegat+pi/3)`
Find the maximum speed of the particle and the maximum acceleration of the particle
View SolutionA particle is subjected to two simple harmonic motions in the same direction having equal amplitudes and equal frequency. If the resultant amplitude is equal to the amplitude of the individual motions, find the phase difference between the individual motions.
View Solution
worked out Examples questions and complete solutions for chapter SIMPLE HARMONIC MOTION of HC VERMA of Class 11