Complete Solutions to FROM SCALAR PRODUCT AND VECTOR PRODUCT of chapter VECTORS SCALARS ELEMENTARY CALCULUS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | VECTORS SCALARS ELEMENTARY CALCULUS |
| S CHAND | FROM SCALAR PRODUCT AND VECTOR PRODUCT |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
If `vec(F ) = hat(i) +2 hat(j) + hat(k) and vec(V) = 4hat(i) - hat(j) + 7hat(k)` what is `vec(F) . vec(v)` ?
View SolutionFind the projection of the vector `vec(P) = 2hat(i) - 3hat(j) + 6 hat(k) ` on the vector `vec(Q) = hat(i) + 2hat(j) + 2hat(k)`
View SolutionGiven `vec(A) = 2hat(i) + 3hat(j) and vec(B) = hat(i) + hat(j)` . What is the vector component of `vec(A)` in the direction of `vec(B)` ?
View SolutionIf `hat(i) and hat(j)` are unit vectors x and y axes repsectively , what is the magnitude and direction of `hat(i) + hat(j) and hat(i) - hat(j)` ?
View SolutionThe result of scalar product and the vector product of two given vectors is zero . If one vector is `hat(i)` what is the other vector ?
View SolutionThe magnitude to two vectors are `sqrt(61) and sqrt(78)` .If their scalar prodcut is ` - 59` , what is the angle between the two vector ?
View SolutionGiven `vec(A) = hat(i) - 2hat(j) - 3hat(k) , vec(B) = 4hat(i) - 2hat(j) + 6hat(k)` .Calculate the angle made by `(vec(A) +vec(B))` with the x - axis ?
View SolutionSimplify : (i) `| vec(a).vec(b)|^(2) +| vec(a) xx vec(b)|^(2)` (ii) `| vec(a).vec(b)|^(2)- |vec(a) xx vec(b)|^(2)`
View SolutionFind the angle between `vec(A) = hat(i) + 2hat(j) - hat(k) and vec(B) = - hat(i) + hat(j) - 2hat(k)`
View SolutionThe diagonals of a parallelogram are given by the vectors `(3 hat(i) + hat(j) + 2hat(k)) and ( hat(i) - 3hat(j) + 4hat(k))` in m . Find the area of the parallelogram .
View SolutionObtain the condition for the two vectors `vec(A) = x_(1) hat(i) + y_(1)hat(j) + z_(1) hat(k) and vec(B) = x_(2) hat(i) = x_(2) hat(i) + y_(2) hat(j) + z_(2) hat(k)` to be parallel ?
View SolutionWhat are the values of the following
`vec(A) . vec(A)`
View SolutionWhat are the values of the following
`vec(A) xx vec(A)`
View SolutionWhat are the values of the following
`vec(B) xx vec(A) , " if " vec(A) xx vec(B) = vec(C )`
View SolutionThe vector `vec(F )` is a force of `3.0` newton making an angle of `60^(@)` with the displacement . `vec(R )` of magnitude `4.0` m , find
the value of the dot product `vec(F) . vec (R )`
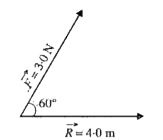
View SolutionThe vector `vec(F )` is a force of `3.0` newton making an angle of `60^(@)` with the displacement . `vec(R )` of magnitude `4.0` m , find
the magnitude and direction of the cross product `vec(R ) xx vec(F )`

View SolutionIf `vec(A) = 5 hat(i) - 3 hat(j) + 4 hat(k) and vec(B) = hat(j) - hat(k) ` , find the sine of the angle between `vec(a) and vec(B) `
View SolutionFind the cross product `vec(r ) xx vec(F) " given " vec(F ) = hat(i) + hat(j) + hat(k) and vec (r )` is the distance between two points whose coordinates are `(-2,3,4) and (1,2,3)`
View SolutionTwo vectors `5hat(i) + 7hat(j) - 3hat(k) and 2 hat(i) + 2hat(j) - a hat(k)` are mutually perpendicular . What is the value of a ?
View SolutionProve that `( vec(A) + vec(B)) xx ( vec(A) - vec(B)) = 2 (vec(B) xx vec(A))`
View Solution
FROM SCALAR PRODUCT AND VECTOR PRODUCT questions and complete solutions for chapter VECTORS SCALARS ELEMENTARY CALCULUS of S CHAND PHYSICS (ENGLISH) of Class 11
All Exercises from S CHAND Class 11 PHYSICS VECTORS SCALARS ELEMENTARY CALCULUS
- ADDITIONAL SOLVED PROBLEMS
- Applications of integration in Physics
- CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS
- EXAMPLES
- FROM SCALAR PRODUCT AND VECTOR PRODUCT
- FROM UNIT VECTORS COMPONENTS OF A VECTOR
- LONG ANSWER QUESTIONS
- SELECTED PROBLEMS (FROM VECTOR ADDITION )
- SHORT ANSWER QUESTIONS
- SOLVED EXAMPLES
- UNSOLVED PROBLEMS
- VERY SHORT ANSWER QUESTIONS