Complete Solutions to EXAMPLE of chapter MOTION OF SYSTEM OF PARTICLES AND RIGID BODY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION OF SYSTEM OF PARTICLES AND RIGID BODY |
| JBD PUBLICATION | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A body is rotating, it is necessary being acted upon by an exteral torque?
View SolutionWhat is the position vector of centre of mass of two particles of equal masses?
View SolutionA heavenly body revolves around a massive star in a highly elliptical orbit..Is its angular momentum constant over the entire orbit?
View SolutionWhere does centre of mass of a triangular lamina lie?
View SolutionIs the angular momentum a scalar quantity ?State its unit.
View SolutionWhat is the direction of angular momentum of a body?
View SolutionIs centre of mass a reality?
View SolutionWhich points on a cylinder rolling over a surface move rectilinearly ?
View SolutionA shell fired from a gun explodes into pieces in air .How is the centre of mass of the shell affected?
View SolutionA ballet-dancer stretches her hands out for slowing down.What principle is involved in this ?
View SolutionUnder what conditions angular momentum of a moving body is zero?
View SolutionThree identical spheres each of radius R are placed touching each oother on a horizontal table. Where is the centre of mass of the system located?
View SolutionCenter of mass of a body always lies at a point, where there is no mass?
View SolutionDoes the angular momentum of an eletron remain consered when the electron otates around a nucleus?
View SolutionWhat is an isolated system?
View SolutionDefine centre of mass.
View SolutionWhat is rotational analogue of mass?
View SolutionIs radius of gyration of a body a constant quantity?
View SolutionAbout which axis is moment of inertia of cube minimum?
View SolutionFind the expression for moment of inertia of a thin uniform rod
about an axis passing through its one end and perpendicular to its length.
View SolutionWhich law is used by a ballet dancer to change her speed or rotation?
View SolutionFind the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be `2MR^2//5`, where M is the mass of the sphere and R is the radius of the sphere.
View SolutionWhat is the ratio of rotational K.E. to the translational K.E. of a rolling body?
View SolutionWhat is the ratio of translational K.E. to the total K.E. of a rolling body?
View SolutionA solid shere and a hollow sphere are allowed to roll down n inclined plane.Which body reaches the bottom earlier?
View SolutionWhat is the condition for rolling of a solid cylinder withuot slipping on an inclined plane?
View SolutionWhat is torque due to gravity about an axis passing through C.M.?
View SolutionWhere does centre of mass of a triangular lamina lie?
View SolutionCan the mass of a body be taken to the concentrated at its CM for calculating its rotational inertia?
View SolutionThree identical spheres each of radius R are placed touching each oother on a horizontal table. Where is the centre of mass of the system located?
View SolutionWhat is the direction of angular momentum of a body?
View SolutionWhich physical quantities are expressed by the following? Moment of lineaer momentum.
View SolutionWhich physical quantities are expressed by the following? Rate of change of angular moementum.
View SolutionWhat is rotational analogue of mass?
View SolutionWhat is ratio of S.I to C.G.S. units of torque?
View SolutionName a physical constant whose dimensins are the same as that of angular momentum.
View SolutionWhich component off force produces no torque?
View SolutionWhere does centre of mass of a triangular lamina lie?
View SolutionFind the torque of a force `(7 hati+3 hatJ-5hatk)`about the origin .the force acts on a particle whoe positio vector is `(hati-hatj+hatk)`.
View SolutionIllustrate with examples, the concept of centre of mass.
View SolutionDefine centre of mass.
View SolutionA wrench with large arm is preferred. Why?
View SolutionWhat is geometrical meaning of angular momentum in two dimensions?
View SolutionWhat is law of conservation of momentum ?
View SolutionThe speed of rotation of a person with some weights in his hands and standing on a rotating platform increases as he draws his arms close to his chest.Why?Explain.
View SolutionWhat is the ratio of translational K.E. to the total K.E. of a rolling body?
View SolutionA sphere is rolling without slippin on a horizontal surface and velocity of its CM.w.r.t,the ground is v,What is linear velocity of :
the point Q highest point as shown in the fig.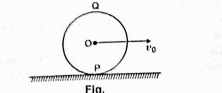 .
.
View SolutionA sphere is rolling without slippin on a horizontal surface and velocity of its CM.w.r.t,the ground is v,What is linear velocity of :
the point Q highest point as shown in the fig. .
.
View SolutionA wheel stays in the upright position while rolling,whereas it falls from its upright position when stationary .Why?
View SolutionWhy are two propellers used in a helicopter?
View SolutionConsider a two - particle system with the particles having masses`M_1` and `M_2` .If the first particle is pushed towards the centre of mass through a distance a,by what distance whould the second particle be moved,so as t keep the centre of mass at the same position?
View SolutionStarting from rest,a fan takes five seconds to attain the maximum speed of 400 rpm.(revolutions per minute) .Assuming constant acceleration,find the time takesn by the fan in attaining half the maximum speed.
View SolutionA block of mass M is places in the top of a biggr block of mass 10 M as shown in fig.All the surfaces are frictionless.The system is released from rest.Find the distance moved by the bigger block at the instant the smaller block reaches the ground.
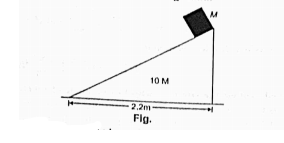 .
.
View SolutionA wheel of radius 10 cm can rotate freely about its centre as shown in fig.A string is wrapped over its rim and is pulled by a force of 5.0N .It is found that the torque prodces an angular acceleration 2.0 rad//s in the wheel.calculate the moment of inertia of the wheel.
View SolutionA wheel rotates with a constant acceleration of `2.0 rad//s^2` .If the wheel starts from rest,how many revolutions will it make in the first 10 seconds?
View SolutionA wheel having moment of inertia 2 kg m^2 about its axis ,rotates at 50 rpm .About this axis .Find the torque that can stop te wheel in one minute.
View SolutionA string is wrapped around the rim of a wheel of moment of inertia `0.20 kg m^2` and radius 20 cm.the wheel is free to rotate about its axis .Initially,the wheel is at rest.The string is now pulled by a force of 20 N.Find the angular velocity of the wheel after 5.0 seconds.
View SolutionA shell fired from a gun explodes into pieces in air .How is the centre of mass of the shell affected?
View SolutionA system consists of two particles of masses M and m(M>m) separated by distanced.What will be the position of CM?
View SolutionThe cap of the pen can be easily opened with the help of tw fingers than with one finger. Explain why.
View SolutionDerive expression for torque in cartesian co-ordinate system.
View SolutionA spinninng top stands erect but a top which is not spinning falls.Why ?
View SolutionA disc spinning about its axis is placed lightly without an translational push on a perfectly frictionless table.Will the cetre of mass of the disc advance?
View SolutionA disc spinning clockwise about its axis with angular velocity `omega_0` is set on a rough horizontal plane[Fig.].
What si the direction of frictional force at point P and sense of frictional torque ,before pure rolling starts?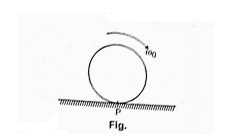 .
.
View SolutionA disc spinning clockwise about its axis with angular velocity `omega_0` is set on a rough horizontal plane[Fig.].
What is the force of friction after rolling without slipping starts? .
.
View SolutionA ring and disc have the same mass and radius.What is the ratio of their moment of inertia about their axis of symmetry?
View SolutionA constant torque acting on a uniform circular wheel changes its angular momentum from L to 4 L in 4 seconds.The magnitude of torque is :
View SolutionWhat is the total kinetic eneryg of a solid sphere rolling on a surface and having translational velocity v?
View SolutionDerive an expression for aceleration of a bdy moving down an inclined plane.
View SolutionMoment of a solid cylinder about its axis of symmetry is equal to moment of inertia about an axis passing through its centre and perpendicular to its length.Show that `L//r = sqrt3`.
View SolutionThe moment of inertia of two bodies are `I_a ` and `I_b` with `I_a>I_b` and their angular moments are equal.Which one of them has greater kinetic energy?
View SolutionDerive Kepler's second law of planetary motion,using the law of conservation of angular momentum.
View SolutionFind the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be `2MR^2//5`, where M is the mass of the sphere and R is the radius of the sphere.
View SolutionIf the earth suddenly contrats to half of its original size without any change in mass,the new duration of the day would be :
View SolutionA cylidrical drum is pushed by a wooden plank as shown in the fig.The cylinder rolls forward on the ground by a distance l/2 equal to half of the length of the plant.there is no slipping at any point of contact.
Where is the board then?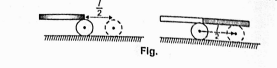 .
.
View SolutionExplain how a cat is able to land gently on its feet after a fall taking the advantage of the law of conervation of angular momentu?
View SolutionRead each statement below carefully, and state, with reasons, if it is true or false :- During rolling, the force of friction acts in the same direction as the direction of motion of the CM of the body.
View SolutionRead each statement below carefully, and state, with reasons, if it is true or false :- The instantaneous speed of the point of contact during rolling is zero.
View SolutionRead each statement below carefully, and state, with reasons, if it is true or false :- The instantaneous acceleration of the point of contact during rolling is zero.
View SolutionRead each statement below carefully, and state, with reasons, if it is true or false :- A wheel moving down a perfectly frictionless inclined plane will undergo slipping (not rolling) motion.
View SolutionA rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N ? What is the linear acceleration of the rope ? Assume that there is no slipping.
View SolutionThe oxygen molecule has a mass of `5.30 xx 10^-26 kg` and a moment of inertia of `1.94xx10^-46 kg m^2` about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is `500 m//s` and that its kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.
View SolutionState the principle of conservation of angular momentum.
View SolutionA flywheel of mass 30 kg has a radius of 0.2 m .What force should be applied tangentially to the rim of the flywheel so that it acquires an angular acceleration of `23 rad//s^2`?
View SolutionWhat is physical significnce of moment of inertia?
View SolutionHow is moment of inertia of a body different from its mass?
View SolutionIf the angular momentum is conserved in a system whose MI is decreased, will its rotational KE be also conserved? Explain.
View SolutionCalculate the radius of gyration of a rod of mass 100 g and length 100 m about an axis passing through is centre of gravity and perpendicular to its length.
View SolutionA thin circular ring od fiameter 15 cm has a mass of 100g.Find its moment of inertia about an axis passing through its centre and perpendicular to its plane.
View SolutionTwo uiform identical rods AB and CD each of mass M and length L are joined to form a cross as a shown in fig.find the moment of inertia of the cross about a bisector as shown dotted in the figure.
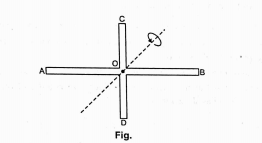 .
.
View SolutionDiscuss general motion of a rigid body.
View SolutionWhat do you understand by couple?
View SolutionGiven that linear momentum of a system of particles is zero.
View SolutionDefine angular momentum and find its relation with moment of inertia.
View SolutionWhat is the moment of inertia of a disc about their diameters?
View SolutionProve that:
`L = I omega`
View SolutionProve that:
`tau = I alpha`
View SolutionProve that
`vecr = vecdL/dt`
View SolutionShow that the area of the triangle contained between the vectors a and b is one half of the magnitude of `a xx b`.
View SolutionProve the theorem of parallel axes.
View Solution
EXAMPLE questions and complete solutions for chapter MOTION OF SYSTEM OF PARTICLES AND RIGID BODY of JBD PUBLICATION of Class 11