A wheel of radius 10 cm can rotate freely about its centre as shown in fig.A string is wrapped over its rim and is pulled by a force of 5.0N .It is found that the torque prodces an angular acceleration 2.0 rad//s in the wheel.calculate the moment of inertia of the wheel.Solution in Punjabi
Step by step video & image solution for A wheel of radius 10 cm can rotate freely about its centre as shown in fig.A string is wrapped over its rim and is pulled by a force of 5.0N .It is found that the torque prodces an angular acceleration 2.0 rad//s in the wheel.calculate the moment of inertia of the wheel. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODYBOOK - JBD PUBLICATIONCHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODYEXERCISE - EXAMPLE
100 Videos
- MODEL TEST PAPER-06BOOK - JBD PUBLICATIONCHAPTER - MODEL TEST PAPER-06EXERCISE - EXERCISE
37 Videos
- Oscillations and WavesBOOK - JBD PUBLICATIONCHAPTER - Oscillations and WavesEXERCISE - EXAMPLE
97 Videos
Similar Questions
A body is rotating, it is necessary being acted upon by an exteral torque?
View SolutionGive an example of a physical quantity which has neither unit nor dimensions.
View SolutionIs S.H.M. always linear?
View SolutionA string is wrapped around the rim of a wheel of moment of inertia 0.20 kg-m^2 nd radius 20 cm. The wheel is free to rotate about it axis. Initially, thewheel is t rest. The string is now pulled by a force of 20 N. Find the angular velocity of the wheel after 5.0 seconds.
View SolutionA wheel of radius 15 cm is rotating about its axis at angluar speed of 20 rad//s . Find the linear speed and total acceleration of a point on the rim.
View SolutionA wheel of radius 0.4m can rotate freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4 kg is hung. An angular acceleration of 8 rad//s^(2) is produced in it due to the torque. Then, the moment of inertia of the wheel is ( g=10m//s^(2) )
View SolutionA constant torque of 31.4 Nm is applied to a pivoted wheel. If the angular acceleration of the wheel is 2pi" rad/s"^(2) , then its moment of inertia is
View SolutionA constant torque of 3.14 N.m is exerted on a pivoted wheel. If the angular acceleration of the wheel is 4pi"rad".s^(-2) , then the moment of inertia of the wheel is
View SolutionA torque of 3.14 N .m constant is applied to a wheel rotating with a mass on the pivot. If the angular acceleration of the wheel is 4 rad / s ^ 2 then what will be the inertia of the wheel?
View Solutionचित्रानुसार, 0.4m त्रिज्या का एक पहिया अपने अक्ष के परितः मुक्त रूप से घूर्णन कर सकता है। एक डोरी को इसकी रिम पर लपेटा गया है तथा इसके सिरे पर 4kg द्रव्यमान लटकाया गया है। बल आघूर्ण के कारण इसमें 8rad−s−2 का कोणीय त्वरण उत्पन्न होता है। तब पहिये का जड़त्व आघूर्ण होगा (g=10ms−2)

View SolutionA wheel of moment of inertia I and radius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.

View SolutionA string is wrapped around the rim of a wheel of moment of inertia 0.20 kg-m^2 and radius 20 cm. The wheel is free to rotate about it axis. Initially, the wheel is at rest. The string is now pulled by a force of 20 N. Find the angular velocity of the wheel after 5.0 seconds.
View SolutionA wheel of radius 0.4 m can rotated freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4 kg is hung, An angular acceleration of 8 rad s−2 is produced in it due to the torque. Then moment inergia of the wheel is (g = 10ms−2)
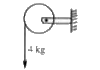
View SolutionA wheel of radius 20 cm can rotate about its centre. A string is wrapped over its rim and is pulled by a force of 10N tangential to pulley. If the angular acceleration produced is 4 rad s−2 then the moment of inertia of the wheel in kg m2 is
View SolutionA constant torque of 3.14 N mis exerted on a pivoted wheel. If the angular acceleration of the wheel is 4πrad/s2 then the moment of inertia of the wheel is
View SolutionA wheel of radius 0.4 m can rotated freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4 kg is hung, An angular acceleration of 8 rad - s−2 is produced in it due to the torque. Then moment inertia of the wheel is (g=10 ms−2)

View Solution
