Show that the area of the triangle contained between the vectors a and b is one half of the magnitude of a×b.Solution in Punjabi
Step by step video & image solution for Show that the area of the triangle contained between the vectors a and b is one half of the magnitude of a xx b. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODYBOOK - JBD PUBLICATIONCHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODYEXERCISE - EXAMPLE
100 Videos
- MODEL TEST PAPER-06BOOK - JBD PUBLICATIONCHAPTER - MODEL TEST PAPER-06EXERCISE - EXERCISE
37 Videos
- Oscillations and WavesBOOK - JBD PUBLICATIONCHAPTER - Oscillations and WavesEXERCISE - EXAMPLE
97 Videos
Similar Questions
A body is rotating, it is necessary being acted upon by an exteral torque?
View SolutionGive an example of a physical quantity which has neither unit nor dimensions.
View SolutionIs S.H.M. always linear?
View SolutionShow that the area of the triangle contained between the vector overset rarr(r ) and overset rarr(b) is one half of the magnitude of overset rarr(a) xx overset rarr(b)
View Solutionदर्शाइए कि →aएवं→b के बीच बने त्रिभुज का क्षेत्रफल →a×→b के परिमाण का आधा है।
View SolutionThe resultant of two vectors A and B is perpendicular to vector A and its magnitude is equal to half of the magnitude of vector B. Then the angle between A and B is
View SolutionThe resultant of two vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between A and B is -
View SolutionShow that the area of the triangle contained between the →aand→b is is one half of the magnitude of →a×→b.
View SolutionThe resultant of two vectors A and B is perpendicular to vector A and its magnitude is equal to half of the magnitude of vector B . Then the angle between A and B is :
(a) 30∘ (b) 45∘
(c) 150∘ (d) 120∘
View SolutionShow that the area of the triangle contained between the vectors a and b is one half of the magnitude of a×b.
View SolutionShow that the area of the triangle contained between the vectors a and b is one half of the magnitude of a × b .
View SolutionShow that the area of the triangle contained between the vector overset rarr(a ) and overset rarr(b) is one half of the magnitude of overset rarr(a) xx overset rarr(b)
View SolutionShow that the area of the triangle contained between the vectors J and $ is one haif0fthe magnitude of →a×→b.
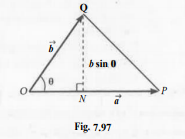
View SolutionShow that the area of the triangle contained between the vectors veca and vecb is one half of the magnitude of vecaxxvecb .
View SolutionIf two vectors are represented by the two sides of a triangle , then show that half the magnitude of their cross product will give the area of the triangle .
View SolutionShow that the area of the triangle contained between the vectors →Aand→B is one-half the magnitude of →A×→B.
View Solution
