Complete Solutions to Exercise2.2 of chapter RELATIONS AND FUNCTIONS of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | RELATIONS AND FUNCTIONS |
| KUMAR PRAKASHAN | Exercise2.2 |
| Number Of Questions | 11 |
| Academic Year | 2023-24 |
Let A={1,2,3....14}. Define a relation R from A to A by `R={(x,y) : 3x-y=0," where "x, y in A}`. Write down its domain, condomain and range.
View SolutionDefine a relation R on the set N of natural numbers by `R= {(x, y): y= x+5,` x is a natural number less than `4, x, y in N).` Depict this relationship using roster form. Write down the domain and the range.
View SolutionA =(1, 2, 3, 5) and B= {4, 6, 9). Define a relation R from A to B by R= {(x, y): the difference between x and y is odd, `x in A, y in B}`. Write R in roster form.
View SolutionThe Fig 2.7 shows a relationship between the sets P and Q. Write this relation
(i) in set-builder form (ii) roster form. What is its domain and range?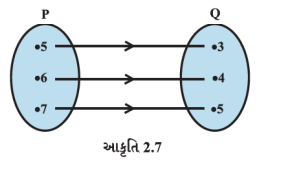
View SolutionLet A= (1, 2, 3, 4, 6). Let R be the relation on A defined by `{(a,b) a, b in A,b` is exactly divisible by a]
(i) Write R in roster form
(ii) Find the domain of R
(iii) Find the range of R.
View SolutionLet A= (1, 2, 3, 4, 6). Let R be the relation on A defined by `{(a,b) a, b in A,b` is exactly divisible by a]
(i) Write R in roster form
(ii) Find the domain of R
(iii) Find the range of R.
View SolutionLet A= (1, 2, 3, 4, 6). Let R be the relation on A defined by `{(a,b) a, b in A,b` is exactly divisible by a]
(i) Write R in roster form
(ii) Find the domain of R
(iii) Find the range of R.
View SolutionDetermine the domain and range of the relation R defined by `R={(x,x+5) : x in [0,1,2,3,4,5}}`.
View SolutionWrite the relation `R= {(x,x^3): x` is a prime number less than 10) in roster form.
View SolutionLet A = {x, y, z) and B = {1, 2}. Find the number of relations from A to B.
View SolutionLet R be the relation on Z defined by `R= {(a,b): a, b in Z, a-b "is an integer").` Find the domain and range of R.
View Solution
Exercise2.2 questions and complete solutions for chapter RELATIONS AND FUNCTIONS of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 11
All Exercises from KUMAR PRAKASHAN Class 11 MATHS RELATIONS AND FUNCTIONS
- Exercise2.1
- Exercise2.2
- Exercise2.3
- Miscellaneous Exercise
- Practice Work
- Solutions of NCERT Exemplar Problems
- Solutions of NCERT Exemplar Problems (Fillers)
- Solutions of NCERT Exemplar Problems (Long Answer Type Questions)
- Solutions of NCERT Exemplar Problems (Objective Type Questions)
- Solutions of NCERT Exemplar Problems (Question of Module)
- Solutions of NCERT Exemplar Problems (True/False)
- Textbook based MCQs
- Textbook Illustrations for Practice Work