Complete Solutions to Practice Work of chapter RELATIONS AND FUNCTIONS of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | RELATIONS AND FUNCTIONS |
| KUMAR PRAKASHAN | Practice Work |
| Number Of Questions | 70 |
| Academic Year | 2023-24 |
Find the value of a and b:
`(2a-5, 4)= (5,b+ 6)`
View SolutionFind the value of a and b:
`(a-3,b+7)= (3,7)`
View SolutionFind the value of a and b:
`(a+2, 4)= (5, 2a + b)`
View SolutionFind the value of a and b:
`(a +1, 1) = (3, b-a)`
View SolutionSet A= {1,2,3,4}, B= {2,4} then verify that `n(A xx B) = n(A) n(B)`.
View SolutionA and B are not singleton sets. `n(A xx B)= 21`. If `A sub B" then "n(B)="………."`.
View SolutionIf a set A has 2 elements then how many elements are there in `n(A xx A xx A)` ?
View SolutionA= {1, 2, 3} and B= { `x : x in N`, x is a prime number less than 5}, Find `A xx B and B xx A`
View SolutionIf `A= {-1, 3,4} and B={2,3}` then find `A xx B, B xx A and A xx A`
View SolutionIf P={1,2}, form the set `P xx P xx P`
View SolutionIf A={-1,1}, find `A xx A xx A`
View SolutionIf `A xx B={(a, x), (a,y),(b,x),(b,y)}`. Find A and B.
View SolutionA = {1, 4} B= {2, 3, 6} and C= {2, 3, 7}, Verify the following result
`A xx (B uu C)= (A xx B) uu (A xx C)`
View SolutionA = {1, 4} B= {2, 3, 6} and C= {2, 3, 7}, Verify the following result
`A xx (B nn C) = (A xx B) nn (A xx C)`
View SolutionA = {1, 4} B= {2, 3, 6} and C= {2, 3, 7}, Verify the following result
`A xx (B-C) = (A xx B) - (A xx C)`
View SolutionIf `a in {-1, 2, 3, 4, 5} and b in {0, 3, 6}`. Write the set of all ordered pairs (a,b) such that `a + b= 5`. How many subset has it?
View SolutionIf A and B are two sets having 3 elements is common. If n(A)= 5, n(B)= 4. find `n(A xx B) and n[(A xx B) nn (B xx A)]`
View SolutionA and B are two sets such that `n(A)= 5` and `n(B)= 2.` If ` (a,2), (b, 3), (c, 2), (d, 2), (e, 2) ` are elements of `A xx B` then find A and B.
View SolutionIf the number of the elements of ordered pairs `A xx A` is 16 and (a, a) (b, a) (a,c) (d,d) are elements of `A xx A` then find A
View Solution`R= {(x, y): x in N, y in N and x + y = 10}`. Write domain and range of R.
View Solution`R = {(a, b): a in N, a lt 5, b= 4}` write domain and range of R.
View SolutionDetermine the domain and range of the relation R defined by `R={(x,x+5) : x in [0,1,2,3,4,5}}`.
View SolutionA relation R from set A= {1, 3, 5, 7} to B= {2, 4, 6, 8} definded as follows: `(x, y) in R hArr x gt y`. Express R as set of ordered pairs.
View Solution`R = {(a, b)": a in N, b in N, a+ 3b = 12}`. Express R as roster method. Find the domain and range of R.
View SolutionTwo dice are tossed. Find whether the following two events A and B are independent :
`A = {(x, y): x + y = 11}` and `B = {(x, y): x ne 5}`
where (x, y) denotes a typical sample point.
View SolutionWrite the following relation in roster from
`R= {(x,y) : 2x + 3y= 12, x in A, y in A}` where `A= {0, 1, 2,3……10}`
View SolutionWrite the following relation in roster from
R= {(x,y): `x in A, yin B`. Y is divisible by x} where A= {5, 6,7, 8} B= {10, 12, 15, 16, 18}
View SolutionThe figure shows a relation between the sets P and Q. write this relation (i) in set builder form (ii) roster form.
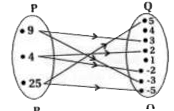
View SolutionThe figure shows a relation between the sets P and Q. write this relation (i) in set builder form (ii) roster form.

View Solution`R= {(x,y): x, y in N, x + y= 8}`. Find the domain and range of R.
View Solution`R`= {`(x, x^(2)): x` is a prime number less then 15} Express R in roster form.
View SolutionThe set A has 3 elements how many relations are there from A to A.
View SolutionThe set A has 4 elements and set B has 2 elements how many relations are there from A to B
View SolutionA= {2, 4, 6, 9} B= {4, 6, 18, 27, 54}
R= {`(a,b): a in A, b in B, a lt b, a` is a factor of b} Find domain and range of R
View SolutionWhich of the following relations are functions? Give reason
`{(3,3) (4,2) (5,1) (6,0) (7,7)} `
View SolutionWhich of the following relations are functions? Give reason
{(2,0), (4,8), (2,1), (3,6)}
View Solution`x= {1, 2, 3, 4},` `y= {1, 5, 9, 11, 15, 16}` which of the following relations are functions from x to y ?
(1) `f_(1)= {(1, 1) (2,11) (3,1) (4, 15)}`
(2) `f_(2)= {(1, 1) (2,7)(3,5)}`
(3) `f_(3)= {(1, 5) (2,9) (3, 1) (4, 5) (2, 11)}`
View SolutionFind the domain and range of the following function
`f(x)= (1)/(sqrt(x-5))`
View SolutionFind the domain and range of the following function
`f(x)= (x-2)/(3-x)`
View SolutionFind the domain and range of the following function
`f(x)= (1)/(1-x^(2))`
View SolutionFind the domain and range of the following function
`f(x)= (x^(2)-1)/(x-1)`
View SolutionIf `f(x)= x^(2 )+ 2x + 3` then find f(1), f(2), f(3)
View SolutionIf `f(x)=(1-x)/(1+x) " then " x=..... .`
View SolutionIf `f(x)= (x-a)^(2) (x-b)^(2)` then find `f(a+b)`
View Solution`f(x)= x^(2)-3x + 4` If `f(x)= f(2x+1)` find the value of `x`.
View SolutionIf `f(x)= x^(3)- (1)/(x^(3))` then show that `f(x)+ f((1)/(x))= 0`
View SolutionFind the range of the following function
`f(x)= sqrt(x-3), x in R`
View SolutionFind the range of the following function
`f(x)= |x-1|, x in R`
View SolutionFind the range of the following function
`f(x)= (4-x)/(x-4), x in R`
View SolutionFind the range of the following function
`f(x)=1- |x-2|, x in R`
View SolutionFind the range of the following function
`f: N rarr R, f(x)= (1)/(x)`
View SolutionFind the range of the following function
`h: N rarr R, h (x)= x- [x]`
View SolutionLet R be a relation on `N xx N` defined by (a,b) `R(c, d) hArr a + d= b + c` for all `(a,b) (c,d) in N xx N` show that,
(a, b) R (a,b) for all `(a, b) in N xx N`
View SolutionLet R be a relation on `N xx N` defined by (a,b) `R(c, d) hArr a + d= b + c` for all `(a,b) (c,d) in N xx N` show that,
`(a,b) R (c, d) rArr (c, d) R (a, b)` for all `(a, b) (c, d) in N xx N`
View SolutionLet R be a relation on `N xx N` defined by (a,b) `R(c, d) hArr a + d= b + c` for all `(a,b) (c,d) in N xx N` show that,
`(a,b) R (c, d) rArr (c, d) R (a, b)` for all `(a, b) (c, d) in N xx N`
View Solution`f:R^(+)rarrR^(+),f(x)=x^2+4(sqrtx)+3` then f(4) = 24.
View Solution`f:R-{0}rarrR,f(x)=(1)/x+px " and "f(1/5)=28/5` then p = …. .
View SolutionFind the domain of the following functions.
`f(x)= (1)/(sqrt(x-|x|))`
View SolutionFind the domain of the following functions.
`f(x)= (1)/(sqrt(x + |x|))`
View SolutionFind the domain of the following functions.
`f(x)= (1)/(sqrt(x-|x|))`
View SolutionFind the domain of the following functions.
`f(x)= (1)/(sqrt(x + |x|))`
View SolutionFind the range and domain of the function defined by `f(x)= (1)/(2- sin 3x)`
View SolutionLet `f(x)=x^(2) and g(x)=2x+1` be two real functions. Find `(f+g) (x), (f-g) (x), (fg) (x), (f/g) (x)`.
View SolutionLet `f(x)=x^(2) and g(x)=2x+1` be two real functions. Find `(f+g) (x), (f-g) (x), (fg) (x), (f/g) (x)`.
View SolutionLet `f(x)=x^(2) and g(x)=2x+1` be two real functions. Find `(f+g) (x), (f-g) (x), (fg) (x), (f/g) (x)`.
View SolutionLet `f(x)=x^(2) and g(x)=2x+1` be two real functions. Find `(f+g) (x), (f-g) (x), (fg) (x), (f/g) (x)`.
View Solution`f(x)= {((2^(x + 2)-16)/(4^(x)-16)",",x ne 2),(k",",x=2):}` f(x) is continuous at x=2 then find k
View SolutionIf `f(x)= 3x^(4)- 5x^(2) + 9` then find `f(x-1)`.
View SolutionIf `f(x)= (x+1)/(x-1)` then show that `f[f(x)] = x`.
View Solution`R = {(a, b): b= |a-1|, a in Z and |a| le 3}`. Find the domain and Range of R
View Solution
Practice Work questions and complete solutions for chapter RELATIONS AND FUNCTIONS of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 11
All Exercises from KUMAR PRAKASHAN Class 11 MATHS RELATIONS AND FUNCTIONS
- Exercise2.1
- Exercise2.2
- Exercise2.3
- Miscellaneous Exercise
- Practice Work
- Solutions of NCERT Exemplar Problems
- Solutions of NCERT Exemplar Problems (Fillers)
- Solutions of NCERT Exemplar Problems (Long Answer Type Questions)
- Solutions of NCERT Exemplar Problems (Objective Type Questions)
- Solutions of NCERT Exemplar Problems (Question of Module)
- Solutions of NCERT Exemplar Problems (True/False)
- Textbook based MCQs
- Textbook Illustrations for Practice Work