Complete Solutions to Textbook Illustrations for Practice Work of chapter RELATIONS AND FUNCTIONS of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | RELATIONS AND FUNCTIONS |
| KUMAR PRAKASHAN | Textbook Illustrations for Practice Work |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
If (x+1, y-2)=(3,1), find the values of x and y.
View SolutionIf P={a,b,c} and Q={r}, form the sets `P xx Q and Q xx P`. Check if the products are equal or not?
View SolutionLet A= {1, 2, 3}, B= {3, 4} and C= {4, 5, 6}. Find
`A xx (B nn C)`
View SolutionLet A= {1, 2, 3}, B= {3, 4} and C= {4, 5, 6}. Find
`(A xx B) nn (A xx C)`
View SolutionLet A= {1, 2, 3}, B= {3, 4} and C= {4, 5, 6}. Find
`(A xx (B uuC)`
View SolutionLet A= {1, 2, 3}, B= {3, 4} and C= {4, 5, 6}. Find
`(A xx B) uu (A xx C)`
View SolutionIf P={1,2}, form the set `P xx P xx P`
View SolutionIf R is the set of all real numbers, what do the cartesian products `R xx R and R xx R xx R` represent?
View SolutionIf `A xx B={(,(p,q),(p,r)),(,(m,q),(m,r)):}}`, find A and B.
View SolutionLet A={1,2,3,4,5,6}. Define a relation R form A to A by R= {(x,y) : y=x+1}
(i) Depict this relation using an arrow diagram.
(ii) Write down the domain, codmain and range of R.
View SolutionLet A={1,2,3....14}. Define a relation R from A to A by `R={(x,y) : 3x-y=0," where "x, y in A}`. Write down its domain, condomain and range.
View SolutionThe figure shows a relation between the sets P and Q. Write this relation (i) in set-builder form, (ii) in roster form. What is its domain and range?
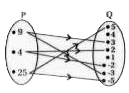
View SolutionLet A={1,2} and B={3,4}. Find the number of relations from A to B.
View SolutionLet N be the set of natural numbers and the relation R be defined on N such that `R={(x,y) : y=2x, y in N}`,
View SolutionExamine each of the following relations given below and state in each case, giving resons whether it is function or not?
(i) R={(2,1), (3,1), (4,2)}, (ii) R={(2,2), (2,4) ,(3,3),(4,4)}
(ii) R={(1,2),(2,3),(3,4),(4,5),(5,6),(6,7)}
View SolutionExamine each of the following relations given below and state in each case, giving resons whether it is function or not?
(i) R={(2,1), (3,1), (4,2)}, (ii) R={(2,2), (2,4) ,(3,3),(4,4)}
(ii) R={(1,2),(2,3),(3,4),(4,5),(5,6),(6,7)}
View SolutionExamine each of the following relations given below and state in each case, giving resons whether it is function or not?
(i) R={(2,1), (3,1), (4,2)}, (ii) R={(2,2), (2,4) ,(3,3),(4,4)}
(ii) R={(1,2),(2,3),(3,4),(4,5),(5,6),(6,7)}
View SolutionLet N be the set of natural numbers. Define a real valued function `f: N to n` by f(x)=2x+1. Using this defination, complete the table given below,

View SolutionDefine the function `f: R to R by y=f(x)=x^(2), x in R`. Complete the Table given below by using this defination. What is the domain and range of this function? Draw the graph of f.

View SolutionDraw the graph of the function `f: R to R` defined by `f(x)=x^(3), x in R`.
View SolutionDefine the real valued function `f: R -{0} to R" defined by "f(x)=1/2 x in R-{0}`. Complete the Table given below using this definition. What is the domain and range of this function?

View SolutionLet `f(x)=x^(2) and g(x)=2x+1` be two real functions. Find `(f+g) (x), (f-g) (x), (fg) (x), (f/g) (x)`.
View SolutionLet `f(x)=sqrtx and g(x)=x` be two functions defined over the set of non-negative real numbers. Find `(f+g) (x), (f-g), (fg) (x) and (f/g) (x)`.
View SolutionLet R be the set of real numbers. Define the real function `f: R to R by f(x)=x+10` and sketch the graph of this function.
View SolutionLet R be a relation from Q to Q defined by `R={(a,b): a,b in Q and a-b in Z}`. Show that
(i) `(a,a) in R" for all " a in Q`
(ii) `(a,b) in R` implies that `(b,a) inR `
(iii) `(a,b) in R and (b,c) in R` implies that `(a,c) in R`
View SolutionLet R be a relation from Q to Q defined by `R={(a,b): a,b in Q and a-b in Z}`. Show that
(i) `(a,a) in R" for all " a in Q`
(ii) `(a,b) in R` implies that `(b,a) inR `
(iii) `(a,b) in R and (b,c) in R` implies that `(a,c) in R`
View SolutionLet R be a relation from Q to Q defined by `R={(a,b): a,b in Q and a-b in Z}`. Show that
(i) `(a,a) in R" for all " a in Q`
(ii) `(a,b) in R` implies that `(b,a) inR `
(iii) `(a,b) in R and (b,c) in R` implies that `(a,c) in R`
View SolutionLet f={(1,1),(2,3),(0,-1),(,-1,-3)} be a linear function from Z into Z. Find f(x).
View SolutionFind the domain of the function `f(x)=(x^(2)+3x+5)/(x^(2)-5x+4)`
View SolutionThe function f is defined by `f(x)={(,1-x,x lt 0),(,1,x=0),(,x+1,x gt 0):}`
Draw the graph of f(x).
View Solution
Textbook Illustrations for Practice Work questions and complete solutions for chapter RELATIONS AND FUNCTIONS of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 11
All Exercises from KUMAR PRAKASHAN Class 11 MATHS RELATIONS AND FUNCTIONS
- Exercise2.1
- Exercise2.2
- Exercise2.3
- Miscellaneous Exercise
- Practice Work
- Solutions of NCERT Exemplar Problems
- Solutions of NCERT Exemplar Problems (Fillers)
- Solutions of NCERT Exemplar Problems (Long Answer Type Questions)
- Solutions of NCERT Exemplar Problems (Objective Type Questions)
- Solutions of NCERT Exemplar Problems (Question of Module)
- Solutions of NCERT Exemplar Problems (True/False)
- Textbook based MCQs
- Textbook Illustrations for Practice Work