Complete Solutions to Passages of chapter THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | THERMODYNAMICS |
| NARAYANA | Passages |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
Graph for one mole gas is given below
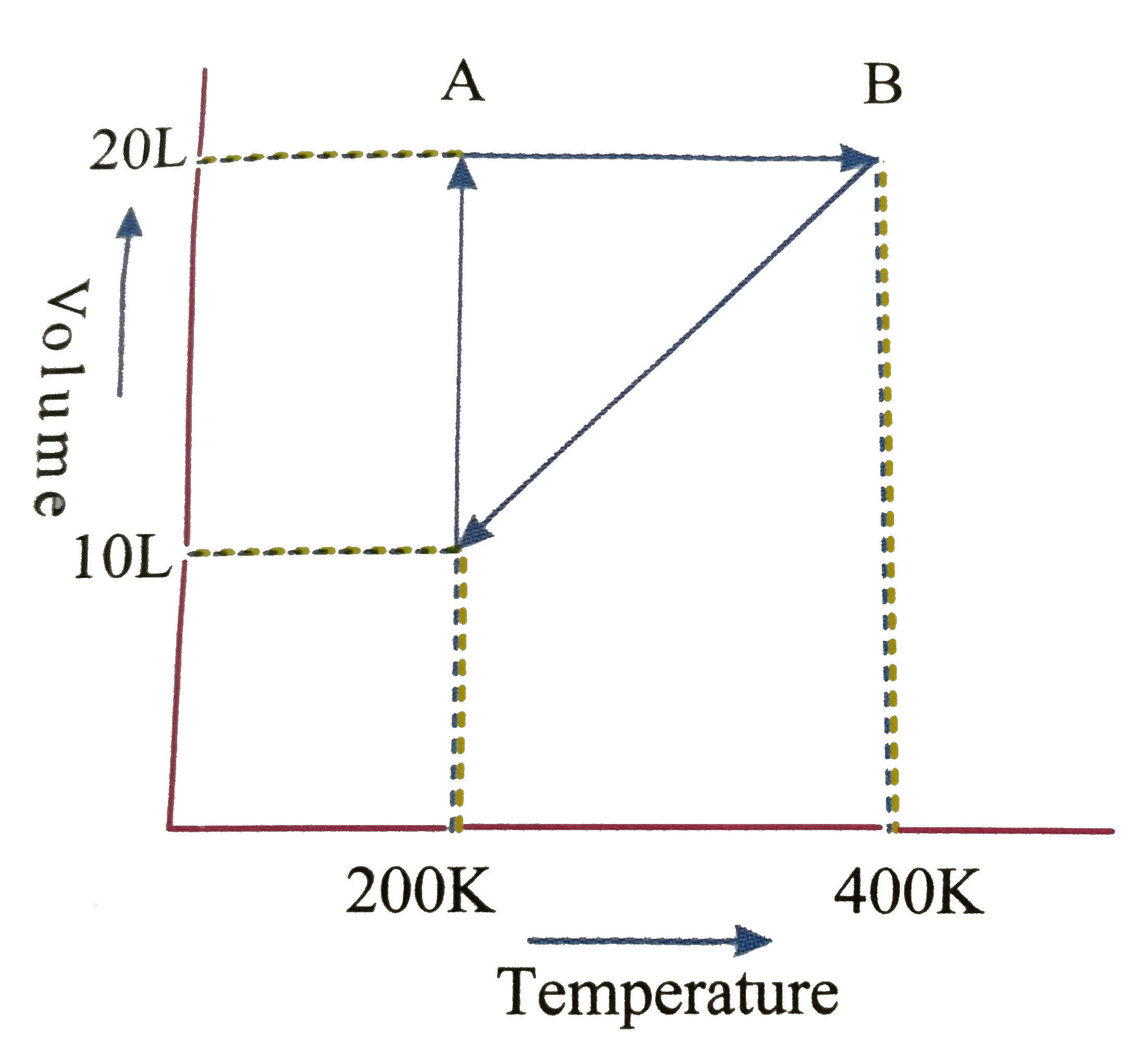
Process, `A rarr B` represents
View SolutionGraph for one mole gas is given below
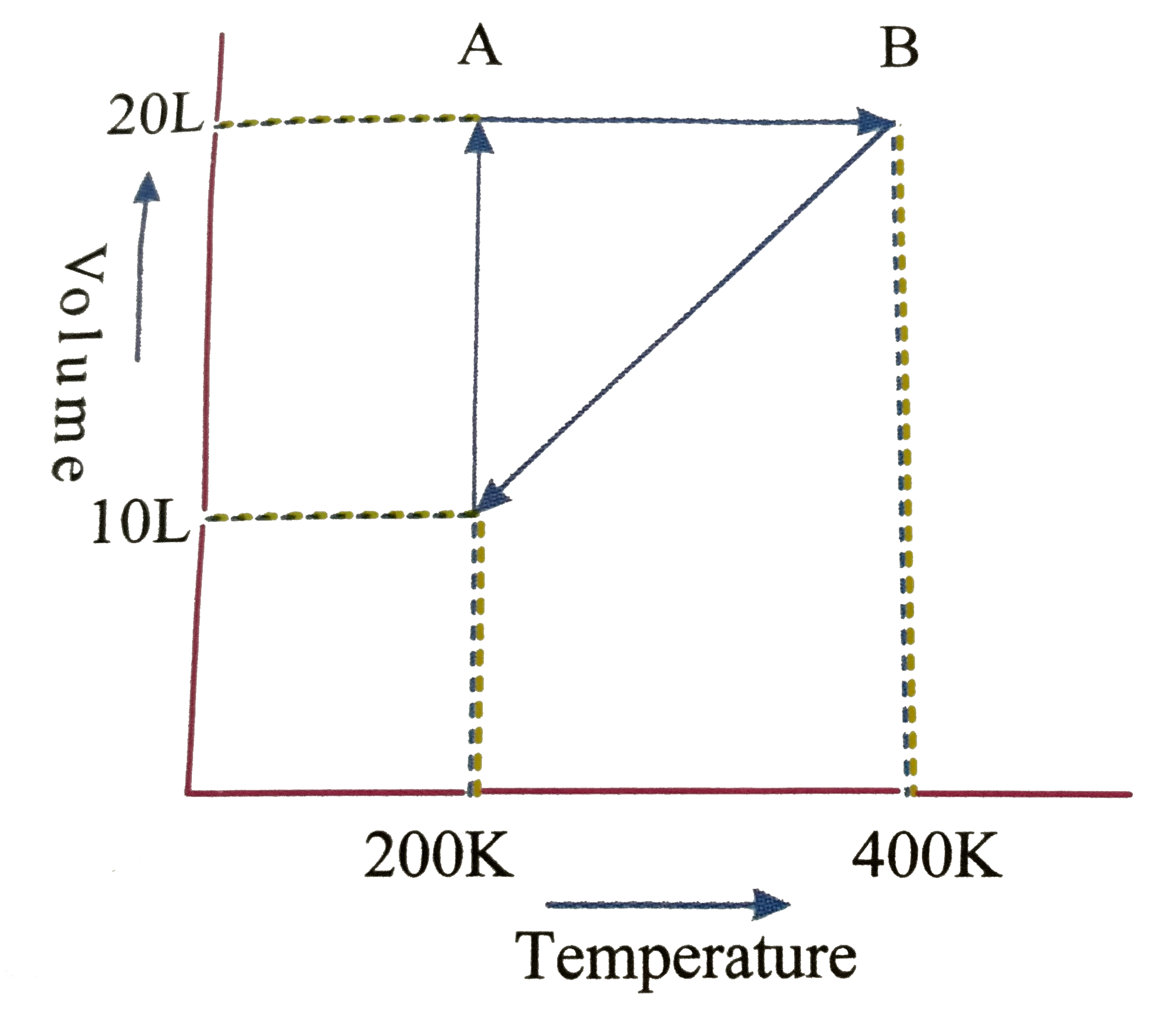
The pressure at C is
View SolutionGraph for one mole gas is given below

Work done in the process `C rarr A` is
View SolutionGraph for one mole gas is given below
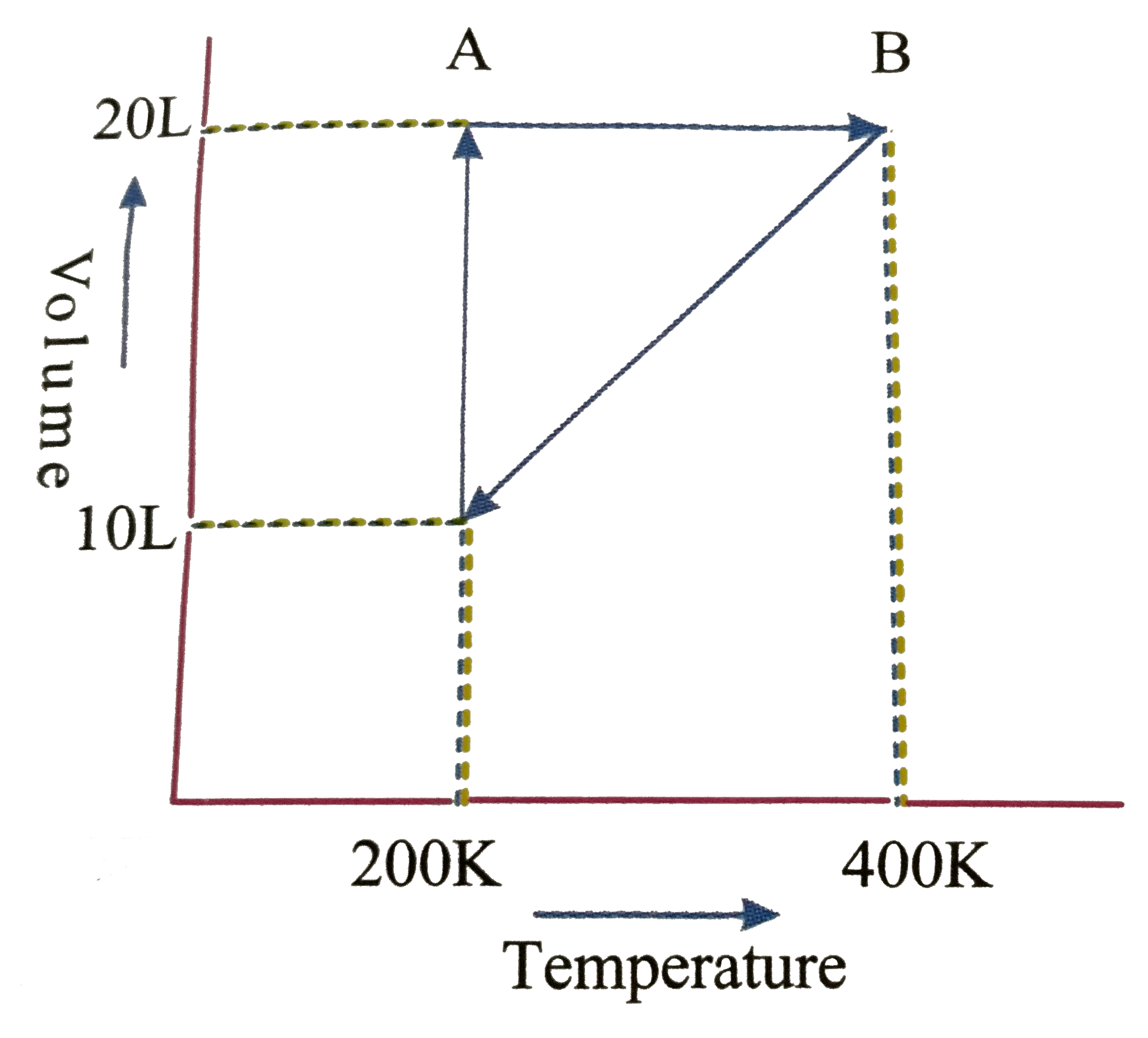
the process which occurs in going from, `B rarr C` is
View SolutionWork is the mode of transference of energy. If the system involves gaseous substance and there is difference of pressure between system and surroundings, such a work is referred to as pressure - volume work `(W_(PV)= -P_(ext)DeltaV)`. It has been observed that reversible work done by the system is the maximum obtainable work. `w_(rev) gt w_(ir r)`
The works of isothermal and adiabatic processes are different from each other. for isothermal reversible proces,
`W_("isothermal reversible")=2.303 nRT log_(10) (V_(2)/V_(1))`
`W_("adiabatic reversible")=C_(V) (T_(1)-T_(2))`
Calculate work done when 1 mole of an ideal gas is expanded reversibly from 20 L to 40 L at a constant temperature of 300 K.
View SolutionWork is the mose of transfrence of energy. If the system involves gaseous substance and there is difference of pressure between system and surroundings, such a work is referred to as pressure - volume work `(W_(PV)= -P_(ext)DeltaV)`. It has been observed that reversible work done by the system is the maximum obtainable work. `w_(rev) gt w_(ir r)`
The works of isothermal and adiabatic processes are different from each other. for isothermal reversible proces,
`W_("isothermal reversible")=2.303 nRT log_(10) (V_(2)/V_(1))`
`W_("adiabatic reversible")=C_(V) (T_(1)-T_(2))`
Calculate work done when 1 mole of an ideal gas is expended reversibly from 20 L to 40 L at a constant temperature of 300 K.
View SolutionWork is the mose of transfrence of energy. If the system involves gaseous substance and there is difference of pressure between system and surroundings, such a work is referred to as pressure - volume work `(W_(PV)= -P_(ext)DeltaV)`. It has been observed that reversible work done by the system is the maximum obtainable work. `w_(rev) gt w_(ir r)`
The works of isothermal and adiabatic processes are different from each other. for isothermal reversible proces,
`W_("isothermal reversible")=2.303 nRT log_(10) (V_(2)/V_(1))`
`W_("adiabatic reversible")=C_(V) (T_(1)-T_(2))`
A thermodynamic system goes in acyclic process as represented in the following `P-V` diagram:
1. For an ideal gas, consider only `P-V` work in going from an initial state
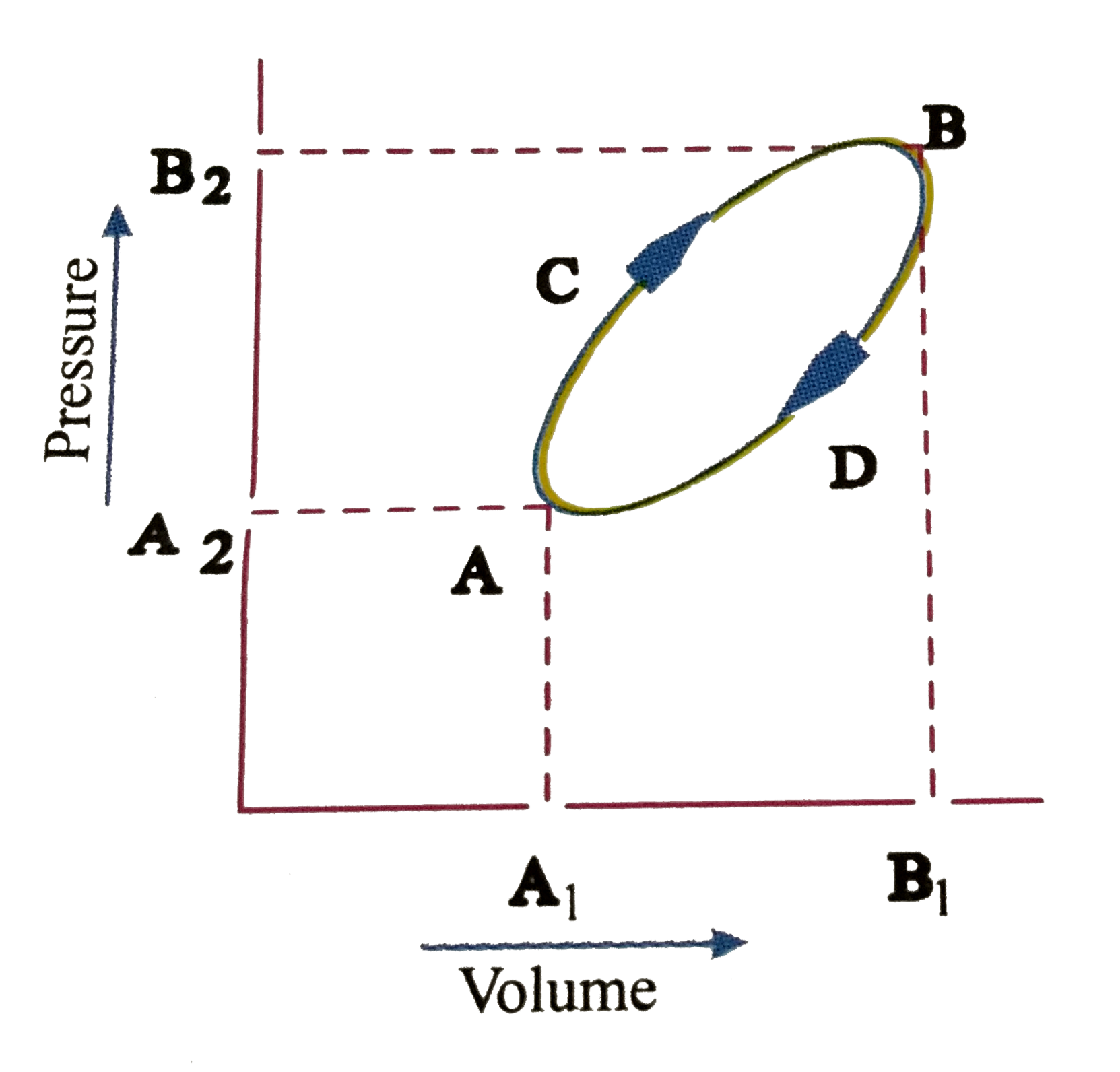
The net work done during the complete cycle is given by the area:
View SolutionA change in the free energy of a system at constant temperature and pressure will be:
`Delta_(sys)G = Delta_(sys)H -T Delta_(sys)S`
At constant temperature and pressure
`Delta_(sys) G lt 0` (spontaneous)
`Delta_(sys)G = 0` (equilibrium)
`Delta_(sys)G gt 0` (non-spontaneous)
If both `DeltaH` and `Deltas` are negative, the reaction will be spontaneous
View Solution`DeltaG` is a thermodynamic prop erty the decrease in which value is the measure of useful work done at constant temperature and pressure:
`DeltaG_("system") lt 0` (spon tan eous) ,
`DeltaG_("system")=0` (equilibrium),
`DeltaG_("system") gt 0` (non- spon tan eous),
Free energy is related to the equilibrium constant, as `DeltaG^(@)=-2.0303 RT log_(10) K_(c)`
A reaction has poaitive values of `DeltaH` and `DeltaS` from this you can deduce that the reaction:
View Solution`DeltaG` is a thermodynamic prop erty the decrease in which value is the measure of useful work done at constant temperature and pressure:
`DeltaG_("system") lt 0` (spon tan eous) ,
`DeltaG_("system")=0` (equilibrium),
`DeltaG_("system") gt 0` (non- spon tan eous),
Free energy is related to the equilibrium constant, as `DeltaG^(@)=-2.0303 RT log_(10) K_(c)`
For a reaction to be spontaneous at all temperatures:
View SolutionThe change in Gibbs free energy of the system alone provides a criterion for the spontaneity of a process at constant temperature and pressure. A change in the free energy of a system at constant temperature and pressure will be :
`DeltaG_("system")=DeltaH_("system")-T DeltaS_(system")`
The free energy for a reaction having
`DeltaH=31400 cal, DeltaS=32 cal L^(-1) mol^(-1)` at `1000^(@)C`
View SolutionA change in the free energy of a system at constant temperature and pressure will be:
`Delta_(sys)G = Delta_(sys)H -T Delta_(sys)S`
At constant temperature and pressure
`Delta_(sys) G lt 0` (spontaneous)
`Delta_(sys)G = 0` (equilibrium)
`Delta_(sys)G gt 0` (non-spontaneous)
For a spontaneous reaction `DeltaG`, equilibrium `K` and `E_(cell)^(Theta)` will be, respectively
View SolutionThe change in Gibbs free energy of the system alone provides a criterion for the spontaneity of a process at constant temperature and pressure. A change in the free energy of a system at constant temperature and pressure will be :
`DeltaG_("system")=DeltaH_("system")-T DeltaS_(system")`
For a system in equilibrium, `DeltaG=0`, under conditions of contant....
View Solution
Passages questions and complete solutions for chapter THERMODYNAMICS of NARAYANA CHEMISTRY (HINGLISH) of Class 11