Complete Solutions to Level-VI of chapter THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | THERMODYNAMICS |
| NARAYANA | Level-VI |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A certain mass of gas expanded from ( 1L, 10 atm) to (4 L, 5 atm) against a constant external pressure of 1 atm. If initial temperature of gas is 300 K and the heat capacity of process is `50 J//^(@)C`. Then the enthalpy change during the process is :
(`1"L" "atm" underline ~ 100 J`)
View SolutionA sample containing 2.000 mol of helium gas originalyy at 298.15 K and 1.000 bar is coled to its normal boilding temperature of 4K, condensed to a liquid and then cooled further to 2K, where it undergoes another phase transition to a second liquid form, called liquid helium II. A beam of laser light suddenly helium II. A beam of laser light suddenly vaporizes this liquid phase, and the helium is brought to a temperature of 298.15K and a pressure of 0.500 bar. the entropy change for the above process is
View SolutionAn athelete is given `100g` of glucose `(C_(6)H_(12)O_(6))` of energy equivalent to `1560 kJ`. He utilises `50%` of this gained enegry in the event. In order to avoid storage of enegry in the body, calculate the weight of water he would need to perspire. The enthalpy of evaporation of water is `441kJ//mol`.
View SolutionConsider the reactions
(i) S (rhombic) `+ 3//2O_(2) (g) rarr SO_(3) (g), Delta H_(1)`
(ii) S (monoclinic) `+3//2O_(2) (g) rarr SO_(3) (g), Delta H_(2)`
(iii) S(rhombic) `+O_(3) (g) rarr SO_(3) (g) , Delta H_(3)`
(iv) S (monoclinic) `+O_(3)(g) rarr SO_(3) (g), Delta H_(4)`
incorrect statement is
View SolutionGvien the following value for the standard molar Gibbs free energy changes?
`G^(@)`, at `25^(@)C`
`Ag^(+) (aq) + 2NH_(3) (l) hArr Ag (NH_(3))_(2)^(+) (aq) ? G^(2) = -41.0KJ (mol Ag^(+))^(-1) Ag^(+) (aq) + Cl^(-)(aq) hArr AgCl (s) ? G^(@) = - 55.6 kJ (mol Ag^(+))^(-1)`
Calculate the value for the thermodynamic equilibrium constant. K, at `25^(@)C` for the reactions:
`AgCl (s) + 2NH_(3) (l) hArr Ag (NH_(3))_(2)^(+) (aq) + Cl (aq)`
View SolutionConsider a classroom that is roughly `5mxx10mxx3m`. Initially `T=27^(@)`C and p=1 atm. There are 50 people in a insulated class losing energy to the room at the average rate of 150 Watt per person. How long can they remain in class if the body temperature is `42^(@)` C and person feels uncomfortable above this temperature. Heat capacity of air=`(7//2)R`
View SolutionConsider the reaction :
`2H_(2) (g) + O_(2) (g) hArr2H_(2)O (g)`
When hyudrogen is ignited in the presence of oxygen, a lot of heat is released and water is produced. At room temperature, the `DeltaH_(r xx n)^(@)` is about `-484 k J//mol` and `Delta S_(r xx n)^(@)` is about -87 kJ/mol. Given this data how would you interpet this thermodynamic process ? Select the correct answer:
View SolutionA reaction from unknown reactants (R) : `R rarr P` is molar entropy of the products (P) is measured to be 460 J/mol K, and 71.3 kJ of heat was given off in the process to the surroundings when 1 mol reacted, then the molar entropy of the reactants has to be
View SolutionOne mole of a monatomic ideal gas initially at a pressure of 2.00 bar and a temperature of 273 K is taken to a final pressure of 4.00 bar by a reversible path defined by `p//V`= constant. Taking `C_(V)` to be equal to 12.5 K `mol^(-1) K^(-1)`, the value of `(Delta U)/(w)` for this process is calculated to be
View SolutionA popular game is ''splatball'', where people use pressurized CO2 cartridges to shoot paint-filled plastic balls at targets and at each other. A typical splatball gun takes a 1.00 L `CO_(2)` catridge filled to 300 PSI pressure. How many work is done as this cartridge is discharged (to atmospheric pressure) when the gun is fired ? (14.7 PSI = 1 atm)
View SolutionThe heat of formation of `C_(2)H_(5)OH(l)` is `-66Kcal//mol` . The heat of combustion of `CH_(3)OCH_(3)(g)` is `-348Kcal//mol` , `DeltaH_(f)` for `H_(2)O` and `CO_(2)` are `-68Kcal//mol` and `-94Kcal//mol` . Respectively. Then, the `DeltaH` for the isomerisation reaction `C_(2)H_(5)OH(l)rarrCH_(3)OCH_(3)(g)` , and `DeltaE` for the same are at `T=25^(@)C`
View SolutionIn the reaction `AB_(2)(I) + 2X_(2) (g) hArr AX_(2) (g) + BX_(2) (g) Delta H = -270` k cal per mol. Of `AB_(2) (I)` the enthalpies of formation of `AX_(2) (g)` & `BX_(2) (g)` are in the ratio of `4 : 3` and have opposite sign. The value of `Delta H_(f)^(0) (AB_(2)(I)) = + 30` k cal/mol. Then
View SolutionWhen a certain amount of ethylene was combusted, 6226 kJ heat was evolved. If heat of combustion of ethylene is 1411 kJ, the volume of `O_(2)` (at STP) that entered into the reaction is :
View SolutionGiven the following reaction :
`P : N_(2)(g)+2O_(2)(g)to2NO_(2)(g),DeltaH_(p)=16.18kcal`
`Q : N_(2)(g)+2O_(2)(g)toN_(2)O_(4)(g),DeltaH_(Q)=2.31kcal`
Based on the above facts :
View SolutionEnthalpy of polymerisation of ethylene, as represented by the reaction ,
`Q : N_(2)(g)+2O_(2)(g)toN_(2)O_(4)(g),DeltaH_(Q)=2.31kcal` is `-100` kJ per mole of ethylene. Given bond enthalpy of `C=C` bond is 600 kJ `mol^(-1)`, enthalpy of `C-C` bond (in kJ mol) will be :
View SolutionHaber's process for production of ammonia `(N_(2) + 3H_(2) hArr NH_(3))` requires `500^(@)C` temperature and 300 atmoshperic pressure, while blue -green algae (a type of vegetation) carry out the same reaction at ambient temperature & pressure by breaking down the activation energy barrier in many small interlinked steps. if `Delta H_(1)` & `Delta H_(2)` represent the enthalpy change for indicated reaction at same reaction conditions by Haber's process & by blue -green algae respectively then:
View SolutionA substance is carried through the following transformations:
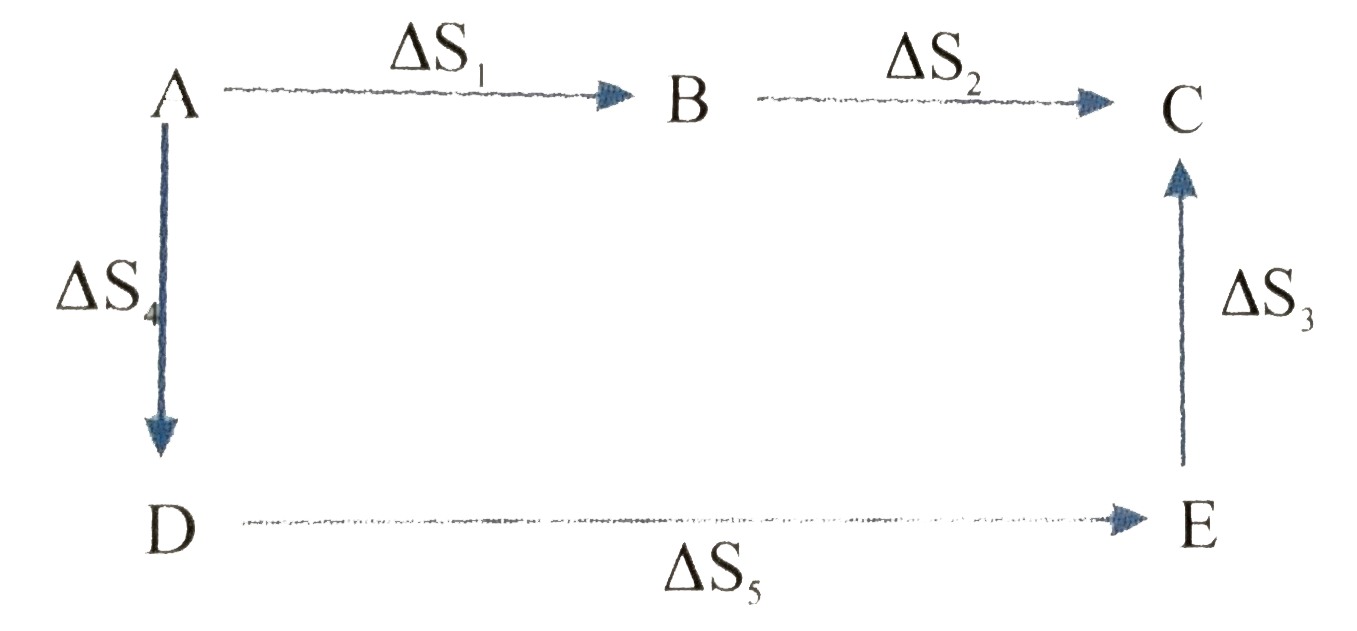
The equation `Delta S_(1) + Delta S_(2) = Delta S_(3) + Delta S_(4) + Delta D_(5)`
View Solution`300K` a gas `(gamma = 5//3)` is compressed adiabatically so that its pressure becomes `1//8` of the original pressure. The final temperature of the gas is :
View SolutionSelect correct statement (s)
View SolutionHow many of the following variable can be used to specify the state of the system. Internal energy, composition, pressure, Temperature, Volume, Work
View SolutionA system undergoes two cyclic processes 1 and 2. Process 1 is reversible and process 2 is irreversible. The correct statement relating to the two processes is
View SolutionA piece of zinc at a temperature of `20.0^(@)` C weighing 63.38 g is dropped into 180 g boiling water `(T= 100^(@)C`) . The specific heat of zinc is `0.400 Jg^(-1@) C` and that of water is `4.20 Jg^(1@) C` . What is the final common temperature reached by both the zinc and water ?
View SolutionDetermine which of the following reaction at constant pressure represent systems that do work on the surrounding environment
(I) `CaO (s) + CO_(2) (g) rarr CaCO_(3) (s)`
(II) `NH_(4)Cl (s) rarr NH_(3) (g) + HCl (g)`
(III) `2NH_(3) (g) rarr N_(2) (g) + 3H_(2) (g)`
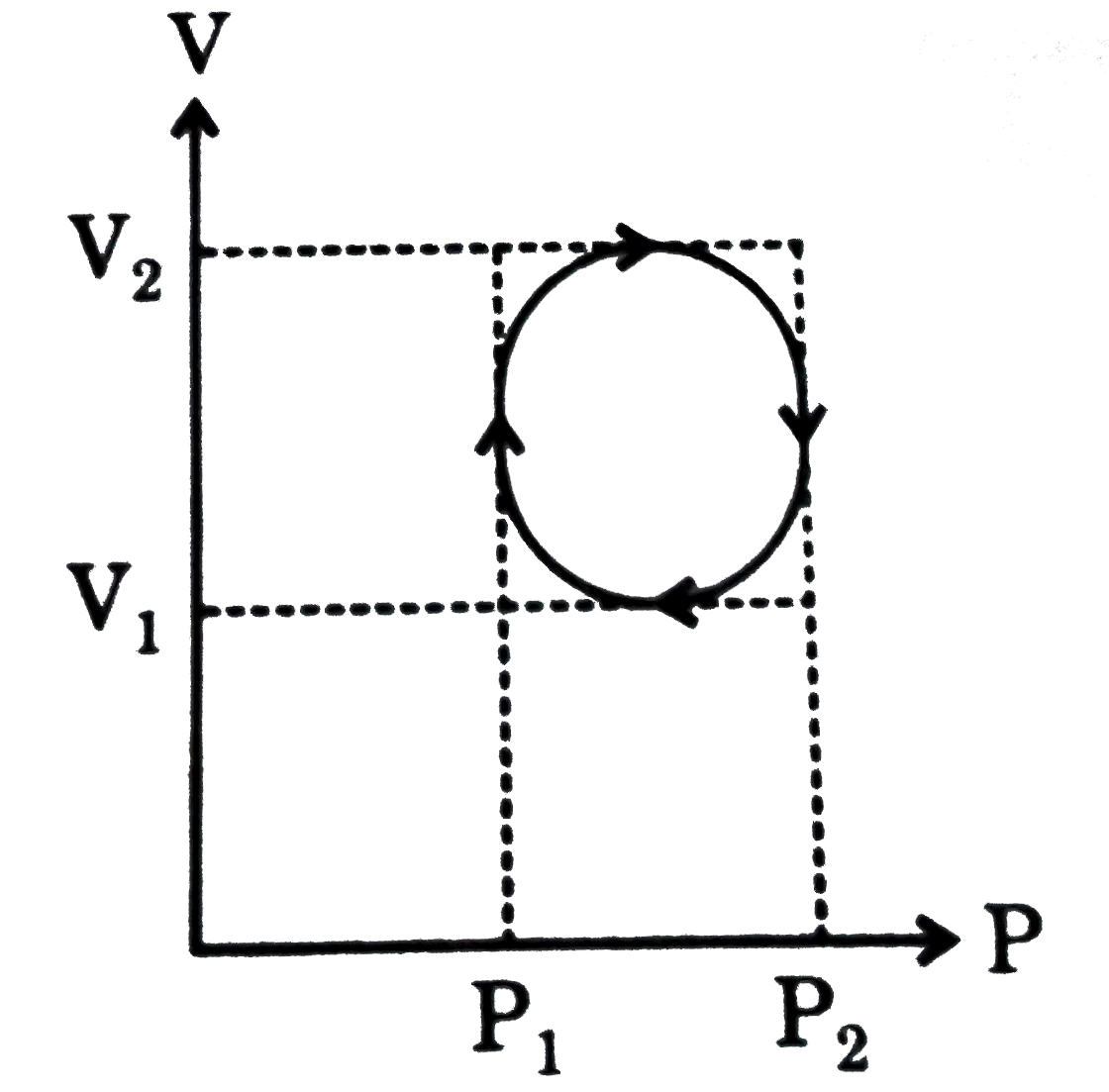
View SolutionIn the cyclic process shown in P-V diagram the magnitude of work done is :
View SolutionOne mole of a non-ideal gas undergoes a change of state `(2.0atm,3.0L,95K)rarr(4.0atm,5.0L,245K)`
With a change in internal energy `DeltaE=30L` atm. The change in enthalpy `(DeltaH)` in the process in `L`-atm is
View SolutionThe reaction `CH_(4) (g) + Cl_(2) (g) rarr CH_(3)Cl (g) + HCl (g)` has `Delta H = -25` kCal.
`{:("Bond","Bond Energy k Cal"),(epsi_(C - Cl),84),(epsi_(H - Cl),103),(epsi_(C - H),x),(epsi_(Cl - Cl),y),(" "x : y = 9 : 5,):}`
From the given data, what is the bond energy of `Cl- Cl` bond (in k.cal)
View SolutionThe standard molar enthalpies of formation of cyclohexane (l) and benzene (l) at `25^(@)C` are `-156` and `+49 kJ mol^(-1)`, respectively. The standard enthaly of hydrogenation of cyclohenxene (l) at `25^(@)C` is `-119 kJ mol^(-1)` Use this data to estimate the magnitude of the resonance enegry of benzene.
View SolutionThe value of `log_(10)K` for a reaction `A hArr B` is (Given: `Delta_(f)H_(298K)^(Theta) =- 54.07 kJ mol^(-1)`,
`Delta_(r)S_(298K)^(Theta) =10 JK^(=1) mol^(-1)`, and `R = 8.314 J K^(-1) mol^(-1)`
View SolutionFind `DeltaG^(@)andDeltaH^(@)` for the reaction
`CO(g)+(1)/(2)O_(2)(g) toCO_(2)(g)at 300K`
when the standard entropy is `-0.094kJ mol^(_1)K^(-1).` The standard Gibbs free energiers fo formation for `CO_(2)andCOare-394.4 and-137.2kJ mol^(-1) respectively.`
View SolutionIn conversion of lime-stone to lime,
`CaCO_(3(s)) to CaO_((s)) + CO_(2(g))` the values of `DeltaH^@` and `DeltaS^@` are `+179.1 kJmol^(-1)` and `160.2 J//K` respectively at `298K` and 1 bar. Assuming that `DeltaH^@` and `DeltaS^@` do not change with temperature, temperature above which conversion of lime-stone to lime will be spontaneous is :
View SolutionThe change in free energy accompainied by the isothermal reversible expansion of 1 mol of an ideal gas when it doubles its volume is `Delta G_(1)`. The change in free energy accompanied by sudden isothermal irreversible doubling volume of 1 mole of the same gas is `Delta G_(2)`. Ratio of `Delta G_(1)` and `Delta G_(2)` is
View SolutionThe following curve represnets the variation of Gibbs function 'G' with pressure at constant temperature.
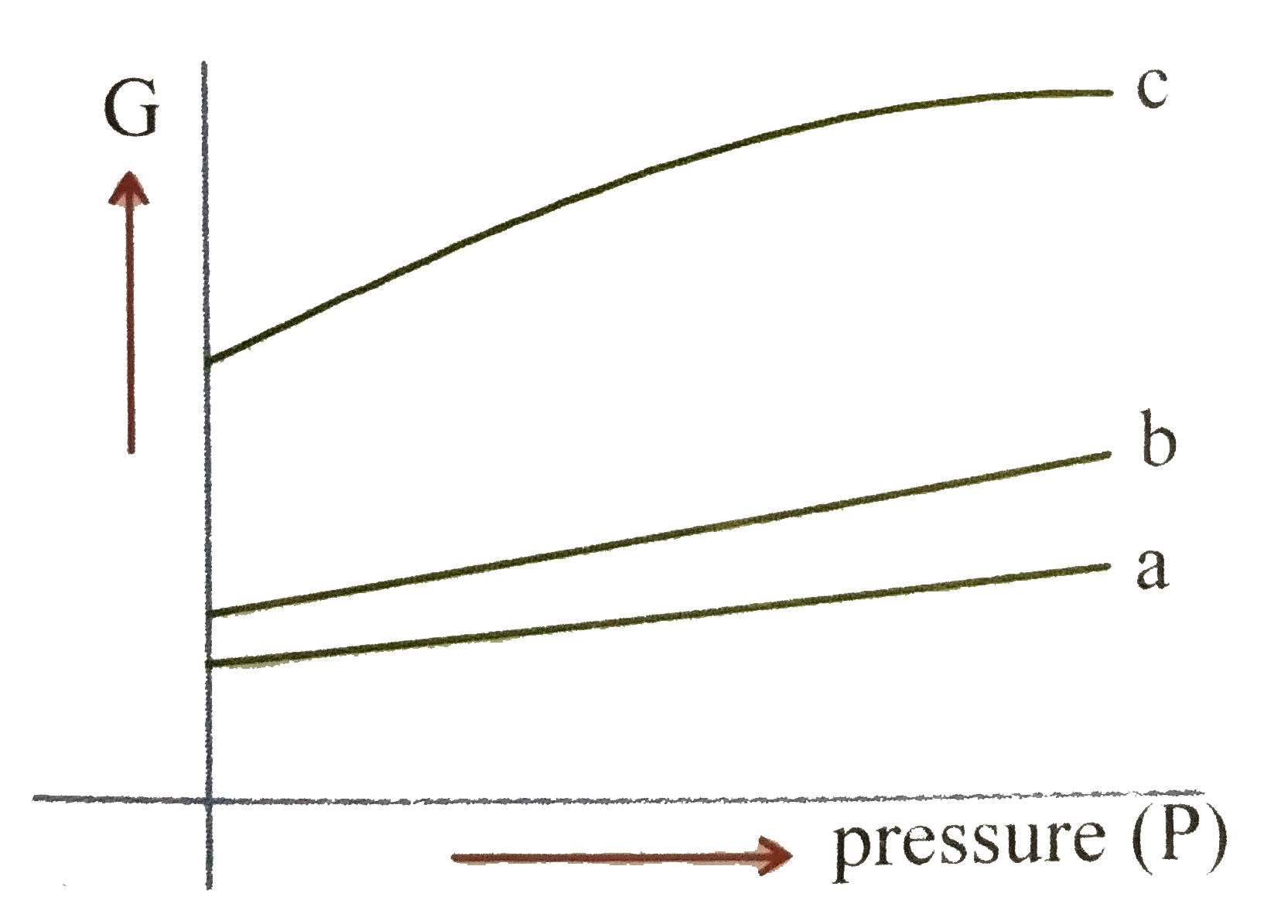
Correct match of given plots with the physical state of a substance is
View SolutionWhich correctly represents the entropy (s) of an isolated system during a process.
View SolutionOne mole of an ideal monoatomic gas expands isothermally against constant external pressure of 1 atm from initial volume of 1L to a state where its final pressure becomes equal to external pressure. If initial temperature of gas is 300K then total entropy change of system in the above process is:
`[R=0.082L atm mol^(-1) K^(-1)-=8.3J mol^(-1) K^(-1)]`
View SolutionAt 1000 K water vapour at 1 atm has been found to be dissociated into `H_(2)` and `O_(2)` to the extent of `3 xx 10^(-5)%`. Calculate the free energy decrease of the system, assuming ideal behavior.
View SolutionWhich of the following graphs best illustrates the variation of entropy of a substance with temp.
View SolutionDuring winters, moisture condenses in the form of dew and can be seen on plant leaves and grass. The entropy of the system in such cases decreases as liquids process lesser disorder as compared to gases. With reference to the second law, which statement is correct. for the above process?
View SolutionA reactions is spontaneous if
View SolutionWhich of the following expressions are correct for an ideal gas ?
View SolutionWhich of the following expression are incorrect for a perfect gas ?
View SolutionFor an ideal gas, an illustration of three different paths `A(B+C)` and `(D+E)` from an initial state `P_(1), V_(1), T_(1)` to a final state `P_(2), V_(2),T_(1)` is shown in the given figure.

Path `A` represents a reversible isothermal expansion form `P_(1),V_(1)` to `P_(2),V_(2)`, Path `(B+C)` represents a reversible adiabatic expansion `(B)` from `P_(1),V_(1),T_(1)to P_(3),V_(2),T_(2)` followed by reversible heating the gas at constant volume `(C)`from `P_(3),V_(2),T_(2)` to `P_(2),V_(2),T_(1)`. Path `(D+E)` represents a reversible expansion at constant pressure `P_(1)(D)` from `P_(1),V_(1),T_(1)` to `P_(1),V_(2),T_(3)` followed by a reversible cooling at constant volume `V_(2)(E)` from `P_(1),V_(2),T_(3) to P_(2),V_(2),T_(1)`.
What is `DeltaS` for path `A`?
View SolutionFor an ideal gas, an illustratio of three different paths `A(B+C)` and `(D+E)` from an initial state `P_(1), V_(1), T_(1)` to a final state `P_(2), V_(2),T_(1)` is shown in the given figure.

Path `A`represents a reversible isothermal expansion form `P_(1),V_(1)` to `P_(2),V_(2)`, Path `(B+C)` represents a reversible adiabatic expansion `(B)` from `P_(1),V_(1),T_(1)to P_(3),V_(2),T_(2)` followed by reversible heating the gas at constant volume `(C)`from `P_(3),V_(2),T_(2)` to `P_(2),V_(2),T_(1)`. Path `(D+E)` represents a reversible expansion at constant pressure `P_(1)(D)` from `P_(1),V_(1),T_(1)` to `P_(1),V_(2),T_(3)` followed by a reversible cooling at constant volume `V_(2)(E)` from `P_(1),V_(2),T_(3) to P_(2),V_(2),T_(1)`.
What is `q_(rev)`, for path `(B +C)`?
View SolutionFor an ideal gas, an illustration of the different paths, A `(B + C)` and `(D + E)` from an intial state `P_(1), V_(1), T_(1)` to a final state `P_(2), V_(2), T_(1)` as shown in the given figure.

Path (A) represents a reversible isothernal expanison from `P_(1)V_(1)` to `P_(2)V_(2)`. Path `(B + C)` represents a reversible adiabatic expansion (B) from `P_(1), V_(1), T_(1)` to `P_(3), V_(2), T_(2)` followed by reversible heating the gas at constant volume (C) from `P_(3), V_(2), T_(2)` to `P_(2), V_(2) T_(1)` to `P_(1) , V_(2), T_(3)` followed by reversible cooling at a constant volume `V_(2)` (E) from `P_(1), V_(2), T_(3)` to `P_(2), V_(2), T_(1)`
What is `Delta S` for path `(D + E)` ?
View SolutionStandard Gibb's energy of reaction `(Delta_(r )G^(@))` at a certain temperature can be computed `Delta_(r )G^(@)=Delta_(r)H^(@)-T.Delta_(r )S^(@)` and the change in the value of `Delta_(r)H^(@)` and `Delta_(r)S^(@)` for a reaction with temperature can be computed as follows :
`Delta_(r )H_(T_(2))^(@)-Delta_(r )H_(T_(1))^(@)=Delta_(r )C_(p)^(@)(T_(2)-T_(1))`
`Delta_(r )S_(T_(2))^(@)-Delta_(r )S_(T_(1))^(@)=Delta_(r )C_(p)^(@)ln.(T_(2)/T_(1))`
`" "Delta_(r )G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)`
and `" by "Delta_(r )G^(@)=-"RT " ln K_(eq)`.
Consider the following reaction : `CO(g)+2H_(2)(g)iffCH_(3)OH(g)`
Given : `Delta_(f)H^(@)(CH_(3)OH,g)=-201 " kJ"//"mol", " "Delta_(f)H^(@)(CO,g)=-114" kJ"//"mol"`
`S^(@)(CH_(3)OH,g)=240" J"//"K-mol, "S^(@)(H_(2),g)=29" JK"^(-1)" mol"^(-1)`
`S^(@)(CO,g)=198 " J"//"mol-K, "C_(p,m)^(@)(H_(2))=28.8 " J"//"mol-K"`
`C_(p,m)^(@)(CO)=29.4 " J"//"mol-K, "C_(p,m)^(@)(CH_(3)OH)=44 " J"//"mol-K"`
and `" "ln ((320)/(300))=0.06`, all data at 300 K
`Delta_(r )S^(@)` at 300 K for the reaction is :
View SolutionStandard Gibb's energy of reaction `(Delta_(r )G^(@))` at a certain temperature can be computed `Delta_(r )G^(@)=Delta_(r)H^(@)-T.Delta_(r )S^(@)` and the change in the value of `Delta_(r)H^(@)` and `Delta_(r)S^(@)` for a reaction with temperature can be computed as follows :
`Delta_(r )H_(T_(2))^(@)-Delta_(r )H_(T_(1))^(@)=Delta_(r )C_(p)^(@)(T_(2)-T_(1))`
`Delta_(r )S_(T_(2))^(@)-Delta_(r )S_(T_(1))^(@)=Delta_(r )C_(p)^(@)ln.(T_(2)/T_(1))`
`" "Delta_(r )G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)`
and `" by "Delta_(r )G^(@)=-"RT " ln K_(eq)`.
Consider the following reaction : `CO(g)+2H_(2)(g)iffCH_(3)OH(g)`
Given : `Delta_(f)H^(@)(CH_(3)OH,g)=-201 " kJ"//"mol", " "Delta_(f)H^(@)(CO,g)=-114" kJ"//"mol"`
`S^(@)(CH_(3)OH,g)=240" J"//"K-mol, "S^(@)(H_(2),g)=29" JK"^(-1)" mol"^(-1)`
`S^(@)(CO,g)=198 " J"//"mol-K, "C_(p,m)^(@)(H_(2))=28.8 " J"//"mol-K"`
`C_(p,m)^(@)(CO)=29.4 " J"//"mol-K, "C_(p,m)^(@)(CH_(3)OH)=44 " J"//"mol-K"`
and `" "ln ((320)/(300))=0.06`, all data at 300 K
`Delta_(r )H^(@)` at 300 K for the reaction is :
View SolutionStandard Gibb's energy of reaction `(Delta_(r )G^(@))` at a certain temperature can be computed `Delta_(r )G^(@)=Delta_(r)H^(@)-T.Delta_(r )S^(@)` and the change in the value of `Delta_(r)H^(@)` and `Delta_(r)S^(@)` for a reaction with temperature can be computed as follows :
`Delta_(r )H_(T_(2))^(@)-Delta_(r )H_(T_(1))^(@)=Delta_(r )C_(p)^(@)(T_(2)-T_(1))`
`Delta_(r )S_(T_(2))^(@)-Delta_(r )S_(T_(1))^(@)=Delta_(r )C_(p)^(@)ln.(T_(2)/T_(1))`
`" "Delta_(r )G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)`
and `" by "Delta_(r )G^(@)=-"RT " ln K_(eq)`.
Consider the following reaction : `CO(g)+2H_(2)(g)iffCH_(3)OH(g)`
Given : `Delta_(f)H^(@)(CH_(3)OH,g)=-201 " kJ"//"mol", " "Delta_(f)H^(@)(CO,g)=-114" kJ"//"mol"`
`S^(@)(CH_(3)OH,g)=240" J"//"K-mol, "S^(@)(H_(2),g)=29" JK"^(-1)" mol"^(-1)`
`S^(@)(CO,g)=198 " J"//"mol-K, "C_(p,m)^(@)(H_(2))=28.8 " J"//"mol-K"`
`C_(p,m)^(@)(CO)=29.4 " J"//"mol-K, "C_(p,m)^(@)(CH_(3)OH)=44 " J"//"mol-K"`
and `" "ln ((320)/(300))=0.06`, all data at 300 K
`Delta_(r )S^(@)` at 320 K is :
View SolutionStandard Gibb's energy of reaction `(Delta_(r )G^(@))` at a certain temperature can be computed `Delta_(r )G^(@)=Delta_(r)H^(@)-T.Delta_(r )S^(@)` and the change in the value of `Delta_(r)H^(@)` and `Delta_(r)S^(@)` for a reaction with temperature can be computed as follows :
`Delta_(r )H_(T_(2))^(@)-Delta_(r )H_(T_(1))^(@)=Delta_(r )C_(p)^(@)(T_(2)-T_(1))`
`Delta_(r )S_(T_(2))^(@)-Delta_(r )S_(T_(1))^(@)=Delta_(r )C_(p)^(@)ln.(T_(2)/T_(1))`
`" "Delta_(r )G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)`
and `" by "Delta_(r )G^(@)=-"RT " ln K_(eq)`.
Consider the following reaction : `CO(g)+2H_(2)(g)iffCH_(3)OH(g)`
Given : `Delta_(f)H^(@)(CH_(3)OH,g)=-201 " kJ"//"mol", " "Delta_(f)H^(@)(CO,g)=-114" kJ"//"mol"`
`S^(@)(CH_(3)OH,g)=240" J"//"K-mol, "S^(@)(H_(2),g)=29" JK"^(-1)" mol"^(-1)`
`S^(@)(CO,g)=198 " J"//"mol-K, "C_(p,m)^(@)(H_(2))=28.8 " J"//"mol-K"`
`C_(p,m)^(@)(CO)=29.4 " J"//"mol-K, "C_(p,m)^(@)(CH_(3)OH)=44 " J"//"mol-K"`
and `" "ln ((320)/(300))=0.06`, all data at 300 K
`Delta_(r )H^(@)` at 320 K is :
View SolutionStandard Gibb's energy of reaction `(Delta_(r )G^(@))` at a certain temperature can be computed `Delta_(r )G^(@)=Delta_(r)H^(@)-T.Delta_(r )S^(@)` and the change in the value of `Delta_(r)H^(@)` and `Delta_(r)S^(@)` for a reaction with temperature can be computed as follows :
`Delta_(r )H_(T_(2))^(@)-Delta_(r )H_(T_(1))^(@)=Delta_(r )C_(p)^(@)(T_(2)-T_(1))`
`Delta_(r )S_(T_(2))^(@)-Delta_(r )S_(T_(1))^(@)=Delta_(r )C_(p)^(@)ln.(T_(2)/T_(1))`
`" "Delta_(r )G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)`
and `" by "Delta_(r )G^(@)=-"RT " ln K_(eq)`.
Consider the following reaction : `CO(g)+2H_(2)(g)iffCH_(3)OH(g)`
Given : `Delta_(f)H^(@)(CH_(3)OH,g)=-201 " kJ"//"mol", " "Delta_(f)H^(@)(CO,g)=-114" kJ"//"mol"`
`S^(@)(CH_(3)OH,g)=240" J"//"K-mol, "S^(@)(H_(2),g)=29" JK"^(-1)" mol"^(-1)`
`S^(@)(CO,g)=198 " J"//"mol-K, "C_(p,m)^(@)(H_(2))=28.8 " J"//"mol-K"`
`C_(p,m)^(@)(CO)=29.4 " J"//"mol-K, "C_(p,m)^(@)(CH_(3)OH)=44 " J"//"mol-K"`
and `" "ln ((320)/(300))=0.06`, all data at 300 K
`Delta_(r )G^(@)` at 320 K is :
View Solution9.0 gm ice `0^(@)C` is mixed with 36 gm of water at `50^(@)C` in a thermally insulated container.using the following data , Answer the qusestion that follow :
`C_(p)(H_(2)O)=4.18Jg^(-1)k^(-1),DeltaH_("fusion ")(ice)=335Jg^(-1)`
final temperature of water is :
View Solution9.0 gm ice `0^(@)C` is mixed with 36 gm of water at `50^(@)C` in a thermally insulated container.using the following data , Answer the qusestion that follow :
`C_(p)(H_(2)O)=4.18Jg^(-1)k^(-1),DeltaH_("fusion ")(ice)=335Jg^(-1)`
`DeltaS_(ice)is:`
View Solution9.0 gm ice `0^(@)C` is mixed with 36 gm of water at `50^(@)C` in a thermally insulated container.using the following data , Answer the qusestion that follow :
`C_(p)(H_(2)O)=4.18Jg^(-1)k^(-1),DeltaH_("fusion ")(ice)=335Jg^(-1)`
`DeltaS_("water")is:`
View Solution9.0 gm ice `0^(@)C` is mixed with 36 gm of water at `50^(@)C` in a thermally insulated container.using the following data , Answer the qusestion that follow :
`C_(p)(H_(2)O)=4.18Jg^(-1)k^(-1),DeltaH_("fusion ")(ice)=335Jg^(-1)`
What I dthe total entropy change in the process?
View SolutionLiquid water freezes at 273 K under external pressure of 1 atm. The process is at equilibrium `H_(2)O (I) hArr H_(2)O (s)` at 273 K & 1 atm However it was required to calculate the thermodyanamic parameters of the fusion prcess occuring at same pressure & different temperature. Using the following data, answer the question that follow.
`d_("ice") = 0.9 gm//c c, d_(H_(2)O(I)) = 1 gm//c c, C_(P) [H_(2)O(s)] = 36.4 JK^(-1) mol^(-1), C_(P) [H_(2)O (I) ] = 75.3 JK^(-1) mol^(-1), Delta H_("fusion") = 6008.2 J mol^(-1)`
The value of `''DeltaH_("fusion")''` at 263 K & 1 atm will be :
View SolutionLiquid water freezes at 273 K under external pressure of 1 atm. The process is at equilibrium `H_(2)O (I) hArr H_(2)O (s)` at 273 K & 1 atm However it was required to calculate the thermodyanamic parameters of the fusion prcess occuring at same pressure & different temperature. Using the following data, answer the question that follow.
`d_("ice") = 0.9 gm//c c, d_(H_(2)O(I)) = 1 gm//c c, C_(P) [H_(2)O(s)] = 36.4 JK^(-1) mol^(-1), C_(P) [H_(2)O (I) ] = 75.3 JK^(-1) mol^(-1), Delta H_("fusion") = 6008.2 J mol^(-1)`
`'' Delta S_("fusion")''` at 263 K & 1 atm will be:
View SolutionThe relation between change in internal energy`(DeltaE)`change in enthalpy`(DeltaH)` and work done`(W)`is represented as
View SolutionThe relation between change in internal energy`(DeltaE)`change in enthalpy`(DeltaH)` and work done`(W)`is represented as
View SolutionThe relation between change in internal energy`(DeltaE)`change in enthalpy`(DeltaH)` and work done`(W)`is represented as
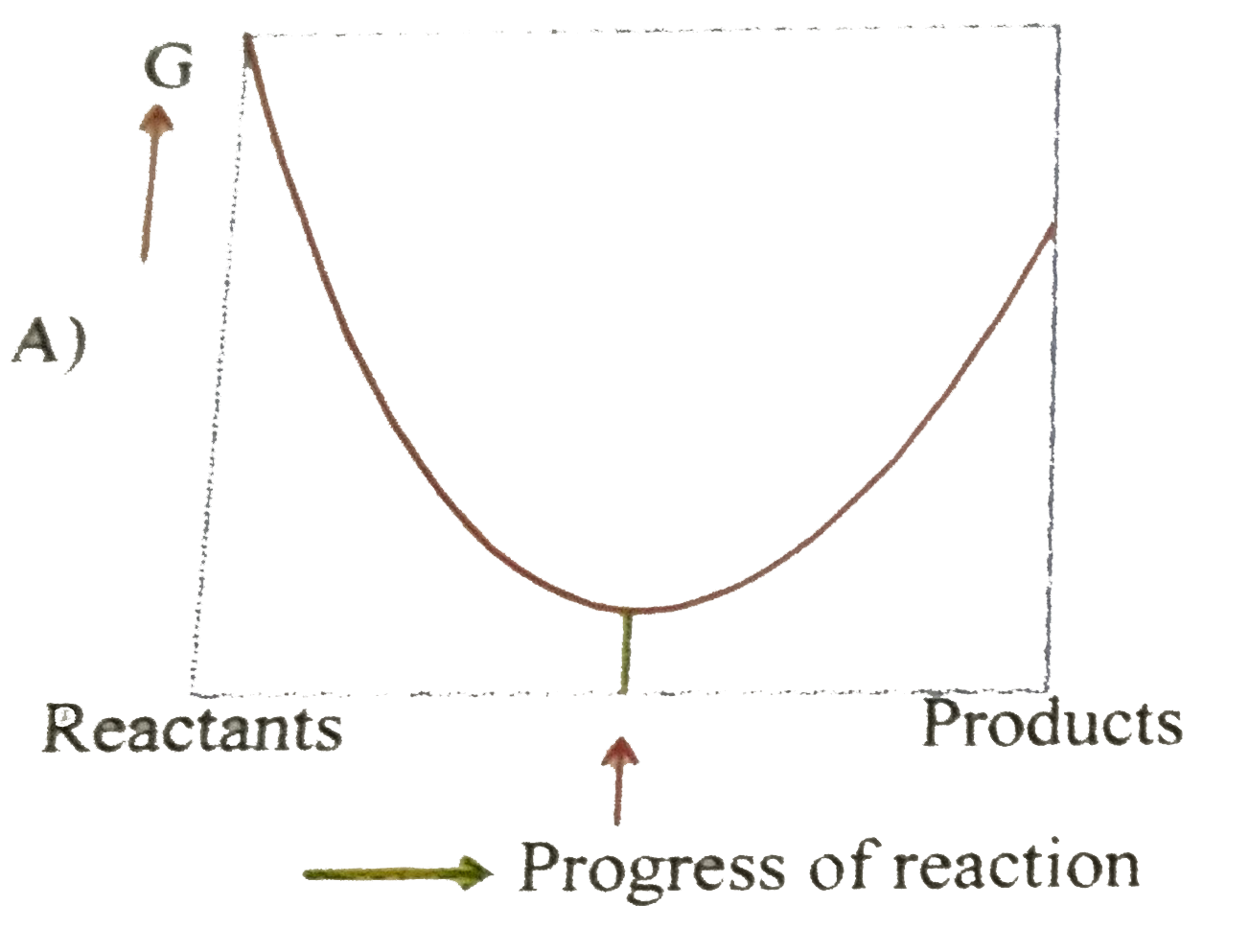
View SolutionFor a reversible reaction at constant temperature and at constant pressure the equilibrium composition of reaction mixture corresponds to the lowest point on Gibbls energy Vs progress of reaction diagrams as shown. At equilibrium Gibbs energy of reaction is equal to zero.
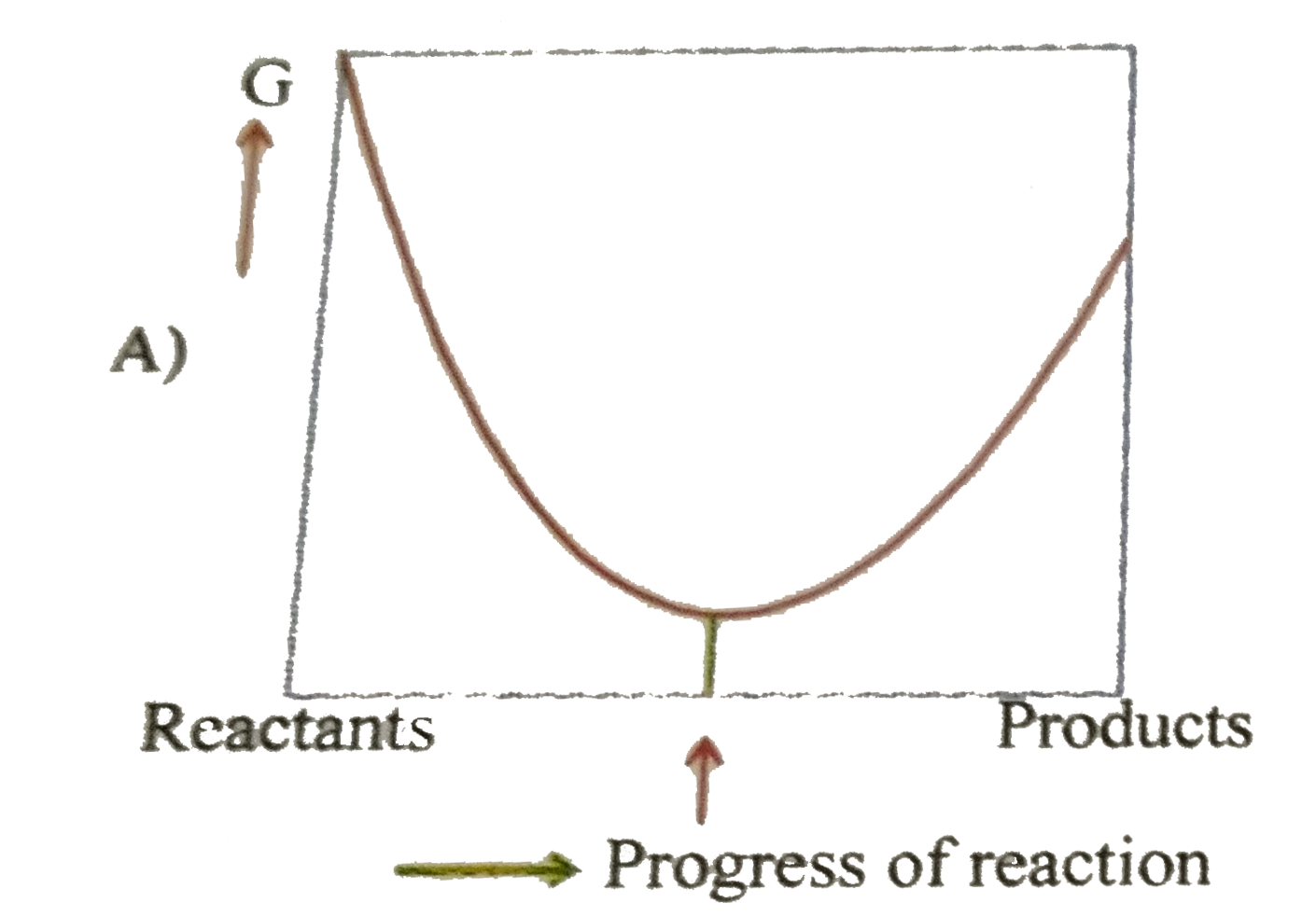
The value of `"log"_(10) K_(eq)` is equal to [`k_(eq)` is the equilibrium coustant]
View SolutionFor a reversible reaction at constant temperature and at constant pressure the equilibrium composition of reaction mixture corresponds to the lowest point on Gibbls energy Vs progress of reaction diagrams as shown. At equilibrium Gibbs energy of reaction is equal to zero.
Which diagram represents the large value of equilibrium constant for the reversible reaction
View SolutionFor a reversible reaction at constant temperature and at constant pressure the equilibrium composition of reaction mixture corresponds to the lowest point on Gibbls energy Vs progress of reaction diagrams as shown. At equilibrium Gibbs energy of reaction is equal to zero.
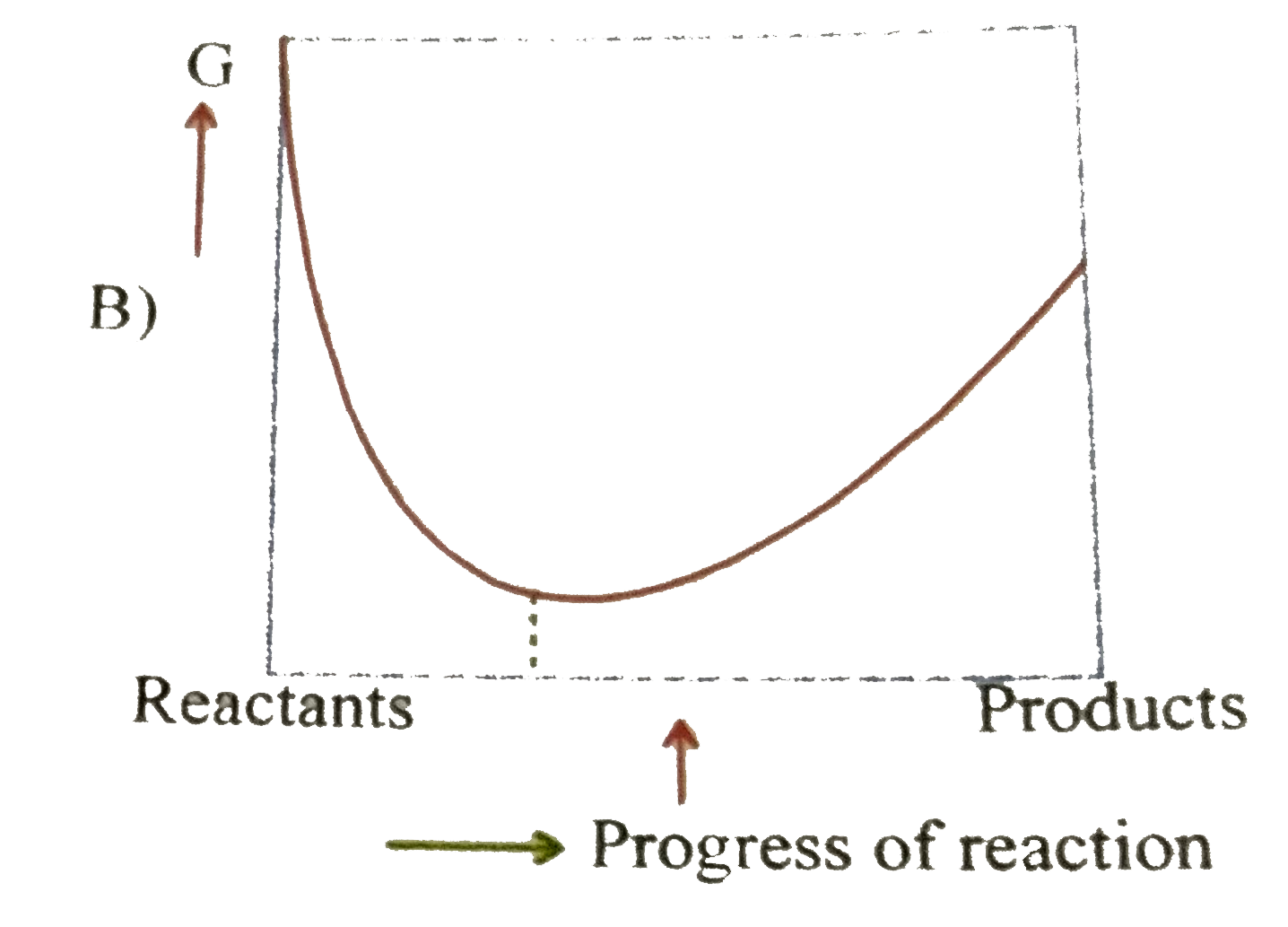
For a reaction
`M_(2)O_((s))^(3//4) rarr 2 M_((S)) + (1)/(2) O_(2 (g)) Delta H = 30 KJ//mol` and `Delta S = 0.07 KJ//mol //K` at 1 atm. The reaction would not be spontaneous at temperature
View SolutionMatch column - I with Colimn - II

View SolutionMatch column - I with Colimn - II

View SolutionMatch the following columns

View SolutionMatch the following columns

View SolutionMatch the following columns

View Solution
View SolutionMatch the following columns
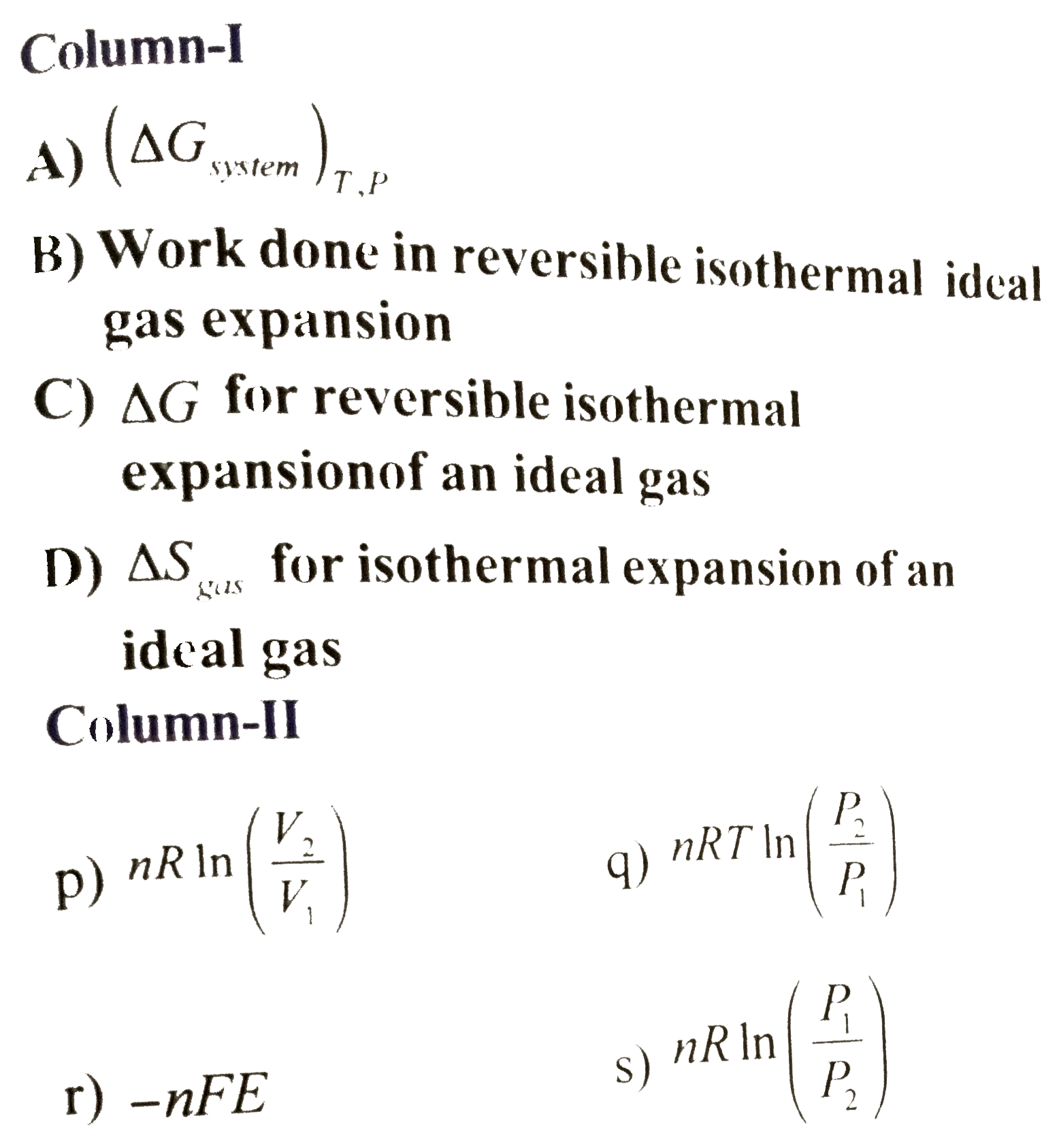
View Solution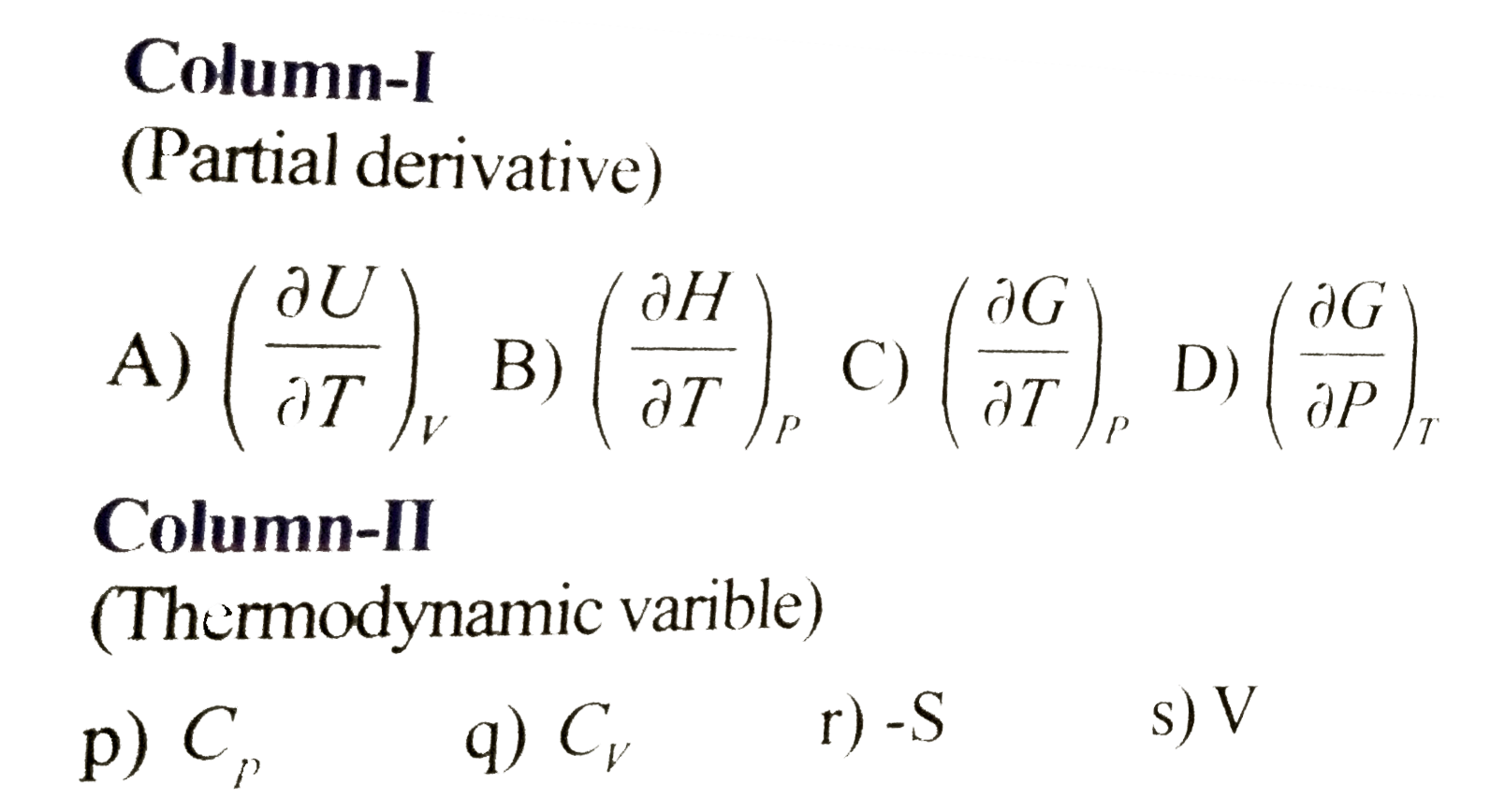
View SolutionStaement -1: The heat absorbed during the isothermal expansion of an ideal gas againt vacuum is zero .
Statement -2: The volume occupied by the molecules of an ideal gas is zero.
View SolutionWork done during isothermal reversible process is given
View SolutionStatement-1: Heat of neutralization of HCl by NaOH is more than that by `NH_(4)OH`
Statement-2: NaOH is stronger base than `NH_(4)OH`
View SolutionStatement: The change in internal energy and change in heat enthalpy does not depend upon the path by which change are brought in.
Explanation: Both `DeltaE` and `DeltaH` are path independent as `E` and `H` are state functions.
View SolutionStatement -1: Entropy change in reversible adiabatic expansion of an ideal gas is zero.
Statement-2: The increase in entropy due to volume increase just compensates the decrease in entropy due to fall in temperature.
View SolutionThe enthalpy change involved in the oxidation of glucose is `-2880 kJ mol^(-1)`. Twently five percent of this energy is available for muscular work. If `100 kJ` of muscular work is needed to walk one kilometer, what is the maximum distance that a person will be able to walk agter eating 125 g of glucose ?
View SolutionCalculate the enthalpy change when infinitely dilute solutions of `CaCl_(2)` and `Na_(2)CO_(3)` are mixed. `Delta_(f)H^(@)` for `Ca_((aq.))^(2+),CO_(3(aq.))^(2-)` and `CaCO_(3(s))` are `-129.80,-161.65` and `288.46kcal//mol` respectively.
View SolutionAn intimate mixture of ferric oxide and aluminium is used as solid fuel in rockets. Calculate the fuel value per `cm^(3)` of the mixture. Heats of formation and densities are as follows:
`H_(f(Al_(2)O_(3)))=-399kcal" "mol^(-1),H_(f(Fe_(2)O_(3)))=-199kcal" "mol^(-1)` ltbr. Density of `Fe_(2)O_(3)=5.2g//cm^(3)," Density of "Al=2.7g//cm^(3)`
View SolutionCalculate the enthalpy change for the following reversible process:
`alpha = T "in" hArr beta - T "in at" 13^(@)C`
1 mol at atm 1 mol at 1 atm
`(Delta H_("trans") = 2288 J mol^(-1))`
View SolutionHeat of neutralization between HCl and NaOH is `-13.7 k.cal`. If heat of neutralization between `CH_(3)COOH` and `NaOH` is `-11.7 k.cal`. Calculate heat of ionization of `CH_(3)COOH`.
View SolutionA gas occupies 2 litre at STP. It is provided 58.63 joule heat so that its volume becomes 2.5litre at 1 atm. Calculate change in its interna energe
View SolutionA sample of ideal gas `(gamma = 1.4)` is heated at constant pressure. If an amount of 85 J of heat is supplied to gas, find `Delta U`.
View SolutionThe free energy change when 1 mole of NaCl is dissolved in water at 298 K. is `-x` KJ find out value of 'x' given-
(a) Lattice energy of NaCl `= 778 kJ mol^(-1)`
(b) Hydratin energy of `NaCl = - 775 kJ mol^(-1)`
(c) Enthropy change at `300 K = 40 J mol^(-1)`
View SolutionCalculate the maximum work done in expanding `16g` of oxygen at `300K` occupying volume of `5dm^(3)` and isothermally untill the volume become `25dm^(3)`?
View SolutionWhat is the entropy change for the conversion of one gram of ice to water at 167 K and one atmospheric pressure ? `[Delta H_("fussion") = 6.025 kJ mol^(-1)]`
View SolutionThe enthalpy of transition of crustalline boron to amorphous boron at `1500^(@)C` is 0.4 kcal "mole"^(-1)`. Assuming at.wt of boron 10, the change in enthaplpy of transition 50 g boron from crystalline to amorphous form is
View SolutionAt `0^(2)C`, if enthalpy of fusion of ice is 1365 kcal/mol. The molar entropy, change for melting of ice at `0^(@)C` is
View SolutionA reaction becomes spontaneous only at 500K. If `Delta H` at 500 K is 3.0 kJ, the change in entropy at 500 K
View SolutionHow much of the following are extensive properties ? Reasistance, Electromotive force, Heat enthalpy , Dipole moment, Heat capacity, Specific Heat, Denisity specific volume
View SolutionHow much of the following are intensive properties ? Vapour pressure, Molarity, Refractive index, Dielectric constant, Osmotic pressure, Molarity, specific gravity, Molar volume
View SolutionOne mole of an ideal gas is heated at constant pressure from `0^(@)C` to `100^(@)C`
(A) Calculate work done. (B) If the gas were expanded isothermally and reversibly at `0^(@)C` from 1 atm to some other pressure `P_(1)`, water must be the final pressure if the maximum work is equal to the work involned in (a)?
View SolutionWater is boiled under a pressure of `1.0 atm`. When an electric current of `0.50A` from a `12V` supply is passed for `300`s through a resistance in thermal contact with it, it is found that `0.789 g` of water is vaporied. Calculate the molar internal enegry and enthalpy chnages at boiling point `(373.15K)`.
View Solution`14 g` oxygen at `0^(@)C` and `10 atm` is subjected to reversible adiabatic expasnion to a pressure of `1atm`. Calculate the work done in
a. Litre atomsphere.
b. Caloride (given, `C_(P)//C_(V) = 1.4)`.
View SolutionCalculate the equilibrium constant for the reaction given below at `400K`, if `DeltaH^(Theta) = 77.2 kJ mol^(-1)` and `DeltaS^(Theta) = 122 J K^(-1) mol^(-1)`
`PCI_(5)(g) rarr PCI_(3)(g) +CI_(2)(g)`
View SolutionCalculate the free enegry change when `1mol` of `NaCI` is dissolved in water at `298K`. Given:
a. Lattice enegry of `NaCI =- 778 kJ mol^(-1)`
b. Hydration energy of `NaCI - 774.3 kJ mol^(-1)`
c. Entropy change at `298 K = 43 J mol^(-1)`
View SolutionHow much heat is required to change `10g` ice at `0^(@)C` to steam at `100^(@)C`? Latent heat of fusion and vaporisation for `H_(2)O` are `80 cl g^(-1)` and `540 cal g^(-1)`, respectively. Specific heat of water is `1cal g^(-1)`.
View SolutionThe vapour pressure of benzene is `1.53 xx 10^(4) Nm^(-2)` at 303 K and `5.2 xx 10^(4) Nm^(-2)` at 333 K. Calculate the mean latent heat of evaportion of benzene over this temprature range
View SolutionMolar heat capacity of `CD_(2)O` (deuterated form of formaldehyde) at constant pressure in `9 cal mol^(-1) K^(-1) at 1000K`. Calculate the entropy change associated with cooling of `3.2 g` of `CD_(2)O` vapour from `1000 to 900K`.
View Solution`1 mol` of an ideal gas at `25^(@)C` is subjected to expand reversibly `10` times of its initial volume. Calculate the change in entropy of expansions.
View SolutionThe standard enthalpy and entropy changes for the reaction in equilibrium for the forward direction are given below:
`CO_((g))+H_(2)O_((g))hArrCO_(2(g))+H_(2(g))`
`DeltaH_(300K)^(@)=-41.16 kJ mol^(-1)`
`DeltaS_(300 K)^(@)=-4.24xx10^(-2) kJ mol^(-1)`
`DeltaH_(1200 K)^(@)=-32.93 K J mol^(-1)`
`DeltaS_(1200 K)^(@)=-2.96xx10^(-2) k J mol^(-1)`
Calculate `K_(p)` at each temperature and predict the direction of reaction at `300 K` and `1200 K`, when `P_(CO)=P_(CO_(2))=P_(H_(2))=P_(H_(2)O)=1` atm at initial state.
View SolutionAt `300K` , the standard enthalpies of formation of `C_(6)H_(5)COOH_((s),CO_(2(g))` and `H_(2)O_((l))` are `-408,-393` and `-286kJ mol^(-1)` respectively. Calculate the heat of combustion of benzoic acid at
`(i)` constant pressure,
`(ii)` constant volume. `(R=8.31J mol^(-1)K^(-1))`
View SolutionThe heat of combusion of glycogen is about `476 kJ mol^(-1)` of carbon. Assume that average heat loss by an adult male is `150W`. If we were to assume that all the heat comes from oxidation of glycogen, how many units of glycogen `(1mol` carbon per unit) must be oxidised per day to provide for this heat loss?
View Solution
Level-VI questions and complete solutions for chapter THERMODYNAMICS of NARAYANA CHEMISTRY (HINGLISH) of Class 11