Complete Solutions to Level-III(C.W) of chapter MOTION IN A PLANE of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN A PLANE |
| NARAYANA | Level-III(C.W) |
| Number Of Questions | 48 |
| Academic Year | 2023-24 |
`BC` is divided into four equal parts by `P,Q` and `R`.The resultant of `vec(AB)` and `3vec(AC)` is

View SolutionA particle moves in the `x-y` plane under the action of a force `vecF` such that the value of its linear momentum `vecP` at any time `t is P_(x) = 2 cos t, P_(y) = 2 sin t`.
The angle `theta` between vecF and vecP` at a given time `t` will be:
View SolutionThree particles `A,B` and `C` start from the origin at the same time,`A` with a velocity `a` along `x`-axis, `B` with a velocity `b` along `y`-axis and `C` with velocity `c` in `XY` plane along the line `x=y`.The magnitude of `c` so that the three always remain collinear is:
View SolutionTwo forces `F_(1)` and `F_(2)` are acting at a point, whose resultant is `F`.If `F_(2)` is doubled `F` is also doubled. If `F_(2)` is reversed then also `F` is doubled. Then `F_(1):F_(2):F` is
View SolutionTwo vectors of equal magnitude `P` are inclined at some angle such that the difference in magitude of resultant and magnitude of either of the vectors is `0.732` times either of the magnitude of vectors. If the angle between them is increased by half of its initial value then find the magnitude of difference of the vectors
View SolutionIf `O` is at equilibrium then the values of the tension `T_(1)` and `T_(2)` are, (`20 N` is acting vertically downwards at `O`).
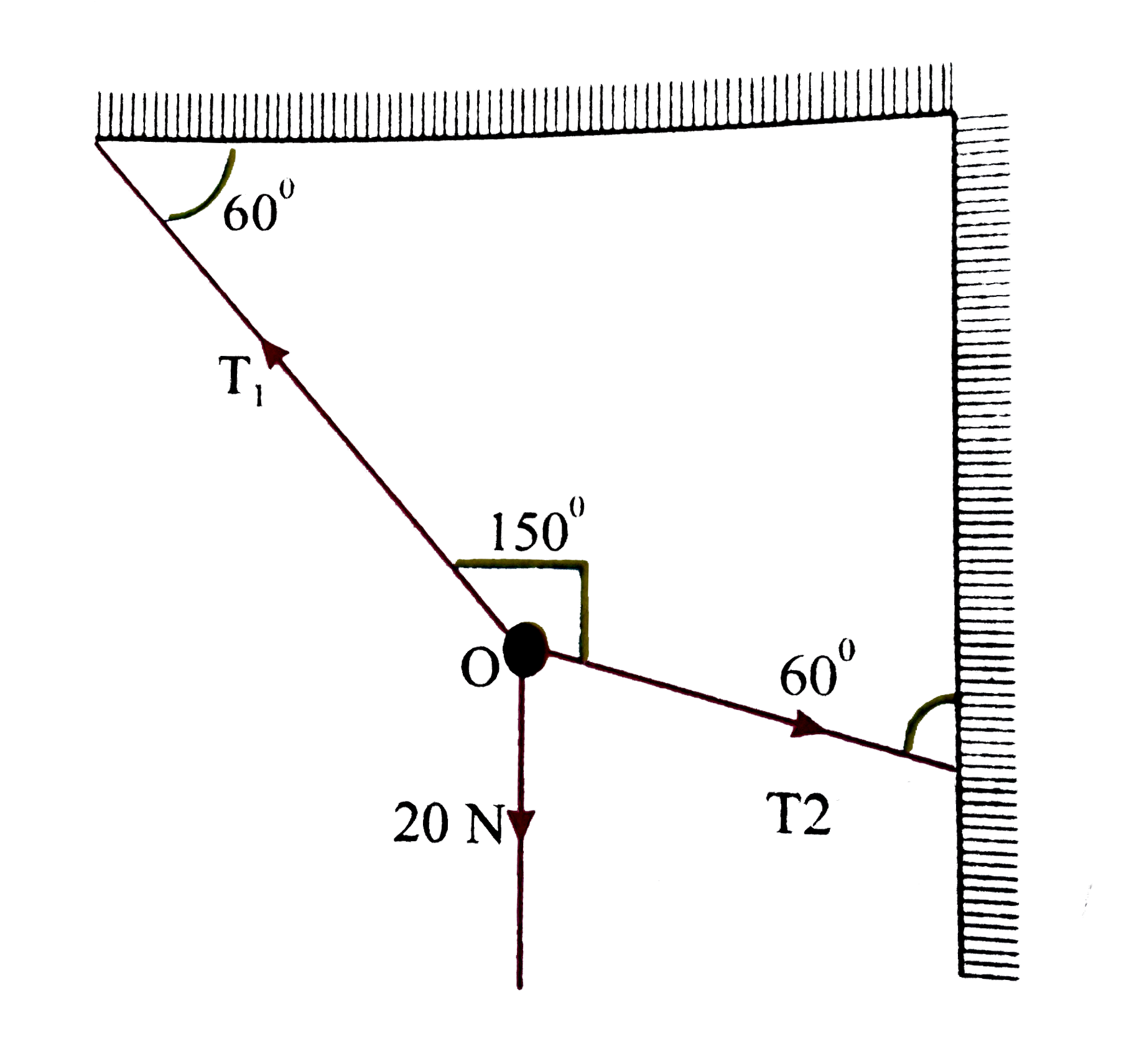
View SolutionA particle starts from the origin at `t=Os` with a velocity of `10.0 hatj m//s` and moves in the `xy`-plane with a constant acceleration of `(8hati+2hatj)m//s^(-2)`. What time is the `x`-coordinate of the particle `16m`?
View SolutionResultant of two vectors of magnitude `P` and `Q` is of magnitude `Q`.If the magnitude of `vecQ` is doubled now the angle made by new resultant with `vecP` is
View SolutionThe two forces `2sqrt2N` and `xN` are acting at a point their resultant is perpendicular to `hatxN` and having magnitude of `sqrt6N`.The angle between the two forces and magnitude of `x` are.
View SolutionThe square of the resultant of two forces `4 N` and `3N` exceeds the square of the resultant of the two forces by `12` when they are mutually perpendicular.The angle between the vectors is.
View SolutionAn aeroplane flies along a straight line from `A` to `B` with a speed `v_(0)`. A steady wind `v` is blowing if `AB=l` then
a)total time for the trip is `(2v_(0)l)/(v_(0)^(2)-v^(2))` if wind blows along the line `AB`
b)total time for the trip is `2l/sqrt(v_(0)^(2)-v^(2))`,if wind blows perpendicular to the line `AB`
c)total time for the trip decrease because of the pressure of wind
d)total time for the trip increase because of the presence of wind
View SolutionTwo particles, 1 and 2, move with constant velocities `v_1` and `v_2` along two mutually perpendicular straight lines toward the intersection point O. At the moment `t=0` the particles were located at the distances `l_1` and `l_2` from the point O. How soon will the distance between the particles become the smallest? What is it equal to?
View SolutionThe distance between two moving particles `P` and `Q` at any time is a.If `v_(r)` be their relative velocity and if `u` and `v` be the components of `v_(r)`, along and perpendicular to `PQ`.The closest distance between `P` and `Q` and time that elapses before they arrive at their nearest distance is
View SolutionTwo ships are `10km` apart on a line from south to north.The one farther north is moving towards west at `40kmph` and the other is moving towards north at `40kmph`.Then distance of their closest approach is
View SolutionTwo stones are projected from the top of a tower in opposite direction, with the same velocity `V` but as `30^(@)` and `60^(@)` with horizontal respectively.The relative velocity of first stone relative to second stone is
View SolutionA motor boat going down stream comes over a floating body at a point `A`. 60 minutes later it turned back and after some time passed the floating body at a distance of `12 km` from the point `A`.Find the velocity of the stream assuming constant velocity for the motor boat in still water.
View SolutionIt is raining at a speed of `5m//s^(-1)` at an angle `37^(@)` to vertical, towards east.`A` man is moving to west with a velocity of `5 m//s^(-1)`.The angle with the vertical at which he has to hold the umbrella to protect himself from rain is.
View SolutionRain, pouring down at an angle `alpha` with the vertical has a speed of `10ms^(-1)`.`A` girl runs against the rain with a speed of `8ms//^(-1)` and sees that the rain makes an angle `beta` with the vertical, then relation between `alpha` and `beta` is
View SolutionA man can swim directly a stream of width `100m` in `4` minutes, when there is no current of water and in `5 minutes` when there is current of water. The velocity of the current of water in the stream is
View SolutionThe velocity of a boat in still water is `10 m//s`.If water flows in the river with a velocity of `6 m//s` what is the difference in times taken to cross the river in the shortest path and the shortest time.The width of the river is `80 m`.
View SolutionA boat takes `4 hrs` to travel certain distance in a river in down stream and it takes `6 hrs` to travel the same distance in upstream. Then the time taken by the boat to travel the same distance in still water is
View SolutionA boatman finds that he can save `6 s` in crossing a river by the quickest path than by the shortest path. If the velocity of the boat and the river be, respectively, `17 ms^-1 and 8 ms^-1`, find the river width.
View SolutionA boy playing on the roof of a `10 m` high building throws a ball with a speed of `10 m//s` at an angle of `30(@)` with the horizontal. How far from the throwing point will the ball be at the height of `10 m` from the ground ?
`[ g = 10m//s^(2) , sin 30^(@) = (1)/(2) , cos 30^(@) = (sqrt(3))/(2)]`
View SolutionAt a given instant of time the position vector of a particle moving in a circle with a velocity `3hati-4hatj+5hatk is hati+9hatj-8hatk`.Its anglular velocity at that time is:
View SolutionA projectile is given an initial velocity of `(hat(i)+2hat(j))` The Cartesian equation of its path is `(g = 10 ms^(-1))` ( Here , `hati` is the unit vector along horizontal and `hatj` is unit vector vertically upwards)
View SolutionA projectile has initially the same horizontal velocity as it would acquire if it had moved from rest with uniform acceleration of `3 m s^-2` for `0.5 min`. If the maximum height reached by it is `80 m`, then the angle of projection is `(g = 10 ms^-2)`.
View SolutionA ball is thrown from a point with a speed `V_(0)`,at an angle of projection `theta`.From the same point and at the same instance a person starts running with a constant speed `V_(0)/sqrt2` to catch the ball will the person be able to catch the ball? If yes, what should be the angle of projection
View SolutionThe coach throws a baseball to a player with an initial speed at `20ms^(-1)` at an angle of `45^(@)` with the horizontal.At the moment the ball is thrown, the player is `50m` from coach.The speed and the direction that the player has to run to catch the ball at the same height at which it was released in `ms^(-1)` is
View SolutionIf a stone is to hit at a point which is at a distance `d` away and at a height `h` (see fig) above the point from where the stone starts,then what is the value of initial speed `u` if the stone is launched at an angle `theta`?

View SolutionIf a projectile crosses two walls of equal height `h` symmetrically as shown in the fig.Choose the correct statement (s) `(g=10m//s^(2))`
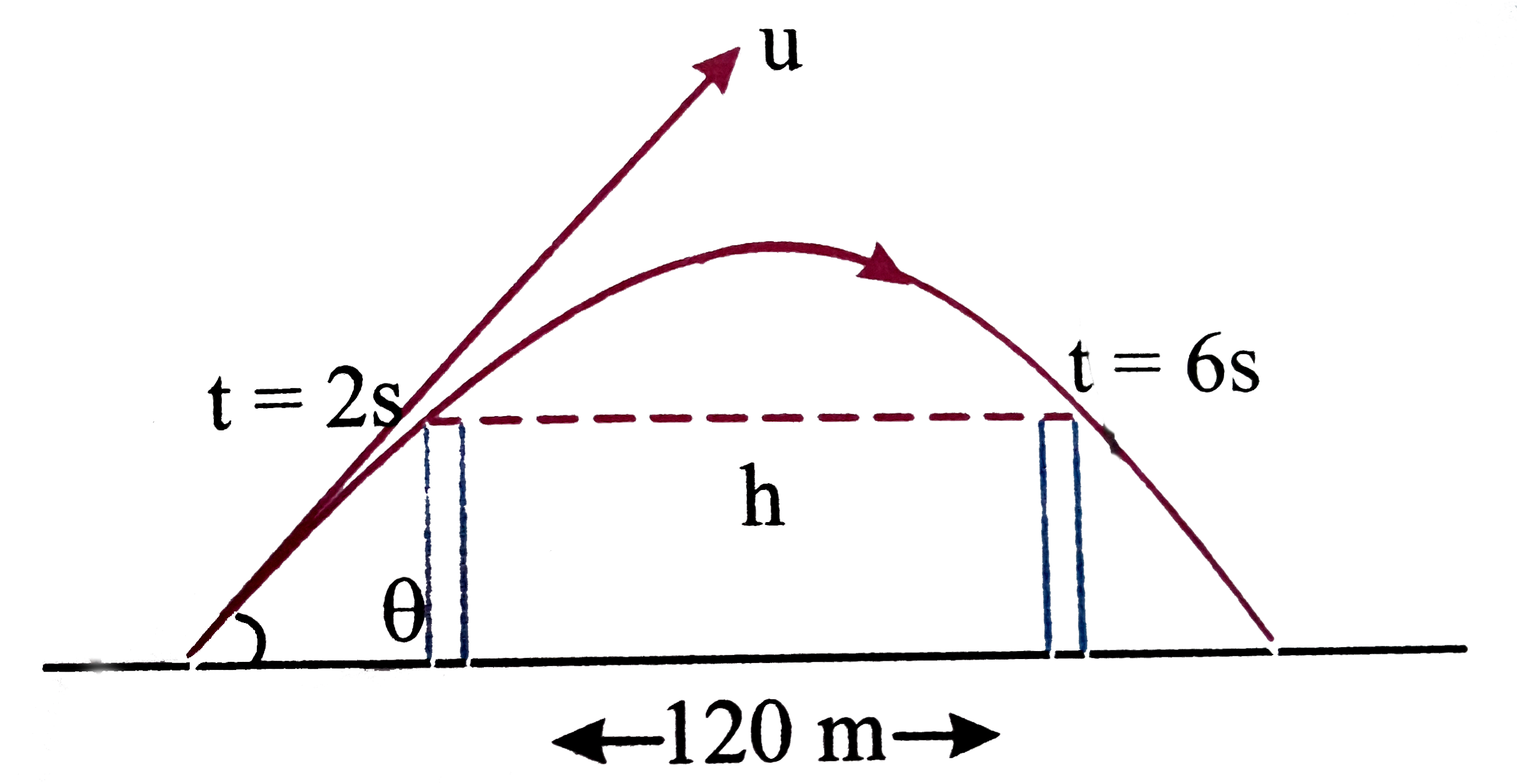
View SolutionA particle is dropped from a height `h`.Another particle which is initially at a horizontal distance `d` from the first is simultaneously projected with a horizontal velocity `u` and the two particles just collide on the ground.Then
View SolutionA ball is projected from the top of a tower with a velocity `3hati+4hatj+5hatk ms^(-1)`,where `hati+hatj+hatk` are unit vectors along east, north and vertical upwards respectively. If the height of the tower is `30 m`, its range is `(g=10 ms^(-1))`
View SolutionA ball is projected from the top of a tower with a velocity `3hati+4hatj+5hatk ms^(-1)`,where `hati+hatj+hatk` are unit vectors along east, north and vertical upwards respectively. If the height of the tower is `30 m`, its time is `(g=10ms^(-1))`
View SolutionA cricketer of height `2.5 m` thrown a ball at an angle of `30^(@)` with the horizontal such that it is received by another crickerter of same height standing at distance of `50m` from the first one.Find the maximum height attained by the ball.
View SolutionA particle when fired at an angle `theta=60^(@)` along the direction of the breadth of a rectangular building of dimension `9mxx8mxx4m` so as to sweep the edges.Find the range of the projectile.
View SolutionA hiker stands on the edge of a cliff `490 m` above the ground and throwns a stone horiozontally with an initial speed of `15ms^(-1)` neglecting air resistance.The time taken by the stone to reach the ground in seconds is `(g=9.8ms^(2))`
View SolutionA hiker stands on the edge of a cliff `490 m` above the ground and throwns a stone horiozontally with an initial speed of `15ms^(-1)` neglecting air resistance.The speed with which it hits the ground in `ms^(-1)` is `(g=9.8ms^(2))`
View SolutionThe direction of a projectile at a certain instant is inclined at an angle `prop` to the horizontal , after `t` second, it is inclined at an angle `beta`. Prove that the horizontal component of the velocity of the projectile is `("gt")/(tan prop - tan beta)`.
View SolutionTwo bodies are projected from the same point with same speed in the directions making an angle `alpha_(1)` and `alpha_(2)` with the horizontal and strike at same point in the horizontal plane through a point of projection. If `t_(1)` and `t_(2)` are their time of flights.Then `(t_(1)^(2)-t_(2)^(2))/(t_(1)^(2)+t_(2)^(2))`
View SolutionAt high altitude , a body explodes at rest into two equal fragments with one fragment receiving horizontal velocity of `10 m//s`. Time taken by the two radius vectors connecting of explosion to fragments to make `90^(@)` is
View SolutionAt a certain height a shell at rest explodes into two equal fragments one of the fragments receives a horizontal velocity `u`.The time interval after which the velocity vectors will be inclined at `120^(@)` to each other is
View SolutionA bomb is rest at the summit of a cliff breaks into two equal fragments.One of the fragments attains a horizontal velocity of `20sqrt3 ms^(-1)`.The horizontal distance between the two fragments, when their displacement vectors is inclined at `60^(@)` relative to each other is `(g=10ms^(-2))`
View SolutionAn object in projected up the inclined at the angle shown in the figure with an initial velocity of `30ms^(-1)`.The distance `x` up the incline at with the object lands is

View SolutionA projectile is fired with a velocity u at right angles to the slope, which is inclined at an angle `theta` with the horizontal. Derive an expression for the distance R to the point of impact.
 .
.
View SolutionIn the time taken by the projectile to reach from `A` to `B` is `t`. Then the distance `AB` is equal to.
 .
.
View SolutionA particle moves on a circle of radius `r` with centripetal acceleration as function of time as `a_c = k^2 r t^2`, where `k` is a positive constant. Find the following quantities as function of time at an instant :
(a) The speed of the particle
(b) The tangential acceleration of the particle
( c) The resultant acceleration, and
(d) Angle made by the resultant with tangential direction.
View SolutionA particle moves in a circular path such that its speed `v` varies with distance `s` as `v = prop sqrt(s)` , where `prop` is a positive constant. Find the acceleration of the particle after traversing a distance `s`.
View SolutionA particle moves in a circle of radius 20 cm. Its linear speed is given by v=2t, where t is in second and v in metre/ second. Find the radial and tangential acceleration at t=3s.
View Solution
Level-III(C.W) questions and complete solutions for chapter MOTION IN A PLANE of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS MOTION IN A PLANE
- C.U.Q
- Example
- Integer
- Level -V Multi answer
- Level -V Passage
- Level -V Single answer
- Level-I (H.W)
- Level-I(C.W)
- Level-II(C.W)
- Level-II(H.W)
- Level-III(C.W)
- Level-Vi Integer
- Level-Vi multiple answer
- Level-VI Passage answer
- Level-Vi single answer
- NCERT BASED QUES. MORE THAN ONE OPTION
- NCERT BASED QUES. PASSAGE
- NCERT BASED QUES. SINGLE ANS.