Complete Solutions to Examples of chapter THERMAL PROPERTIES OF MATTER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | THERMAL PROPERTIES OF MATTER |
| NARAYANA | Examples |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
The graph between two temperature scales `A` and `B` is shown in Fig. Between upper fixed point and lower fixed point there are `150` equal divisions on scales `A` and `100` on scale `B`. The relation between the temperature in two scales is given by_
_S01_001_Q01.png)
View SolutionAt what temperature the Fahrenheit and kelvin scales of temperature give the same reading ?
View SolutionAt what temperature is the Fahrenheit scale reading equal to
(a) twice (b) half of Celsius ?
View SolutionAn accurate Celsius rhwemometer and a faulty Fahrenheit thermometer register `60^(@)` and `141^(@)` respectively when placed in the same constant temperature enclosure. What is the error in the Fahrenheit thermometer ?
View SolutionTwo absolute scale `X` and `Y` have triple points of water defined to be `300 X` and `450 Y`. How are `T_(X)` and `T_(Y)` related to each other ?
View SolutionThe readings corresponding to the ice point and steam point for a constant pressure gas thermometer are `500 cc`, and `545 cc`. If the reading corresponding to room temperature be `510 cc`, find the room temperature ?
View SolutionA constant volume gas thermometer shows pressure readings of `50 cm` and `90 cm` of mercury at `0^(0)C` and `100^(0)C` respectively. What is the temperature on gas scale when the pressure reading is `60 cm` of mercury ?
View SolutionThe resistance of a platinum wire is `15 Omega` at `20^(@)C`. This wire is put in hot furnace and lthe resistance of the wire is found to be `40 Omega`. Find the temperature of the hot furnace if temperature coefficient of resistance of platinum is `3.6 xx 10^(-3)^(0)C^(-1)`
View SolutionThe resistance of a platinum resistance thermomter is found to be `11.0 ohm` when dipped in a triple point cell. When it is dipped in a both,resistance is found to be `28.887 ohm`. Find the temperature of the bath in `.^(0)C` on platinum scale.
View SolutionGraph shows the relation between Centigrade and Fahrenheit scales of temperature. Find the slope in each graph?
View SolutionWhat length of brass and iron at `0^(0)C` must be used if the difference between their lengths is always `0.2m`? The values of `alpha` for brass and iron and `18 xx 10^(-6)//0 C` and `12 xx 10^(-6)//0 C` respectively,
View SolutionA blacksmith fixes iron ring on the rim of the wooden wheel of a bullock cart. The diameter of the rim and the ring are `5.243 m` and `5.231 m` respectively at `27^(@)C`. To what temperature should the ring be heated so as to fit the rim of the wheel ? Coefficient of linear expansion of iron =` 1.20 xx 10^(-5) K^(-1)`
View SolutionAn aluminium measuring rod, which is correct at `5^@C` measures the length of a line as 80 cm at `45^@C` If thermal coefficient of linear expansion of aluminium is `2.50xx10^(-4)//^@C`, the correct length of the line is:
View SolutionAn iron of length `50cm` is joined at an end to copper rod to length `100cm` at `20^(0)C.` Find the length of the system at `100^(0)C` and average coefficient of linear expansion of the systeam.
`(*_(iron) = 12 xx 10^(-6 //0)C and*_(copper) = 17 xx 10^(-6 //0)C.)`
View SolutionDensity of gold is `19.30 g//cm^(3)` at `20^(0)C`. Computer the density of gold at `90^(0)C` by adding steam to it. `(alpha = 14.2 xx 10^(-6 //0) C)`
View SolutionA uniform pressure P is exerted by an external agent on all sides of a solid cube at temperature `t^(@)C`. By what amount should the temperature of the cube be raised in order to bring its volume back to its original volume before the pressure was applied if the bulk modulus is B and co-efficient of volumetric expansion is `gamma`?
View SolutionThe balance wheel of a mechanical wriest watch has a frequency of oscillation given by `f = ((1)/2pi) sqrt(C//I)`, where `I` is the moment of inertia of the wheel and `C` is the torisonal rigidity of its spring. The wrist watch keeps accurate time at `25^(0)C`, How many seconds would it gain a day at `.-25^(0)C` if the balance wheel made of aluminium ?
(Given, `alpha_(Al) = 25.5 xx 10^(-6//0)C)`
View SolutionA clock with a metallic pendulum gains 5 s each day at a temperature of `15^@C` and loses 10 s each day at a temperature of `30^@C`. Find the coefficient of thermal expansion of the pendulum metal.
View SolutionA steel bar of cross sectional area `1 cm^(2)` and `50 cm` long at `30^(0)C` fits into the space between two fixed supports.. If the bar `s` now heated to `280^(0)C`, what force will it exert against the supports ? (`*` for steel `= 11 xx 10^(6//0)C` and Young's modulus for steel `= 2 xx 10^(11) N//m^(2)`)
View SolutionA mass of `2Kg` is suspended from a fixed point by a wire of length `3m` and diameter `0.5 mm`. Initially the wire is just unstretched, the mass resting on a fixed support. By how much must the temperature fall if the mass is to be entirely supported by the wire (Given `Y` for wire `= 206 G Pa, alpha = 11 xx 10^(-6//@)C`)
View SolutionA metallic rod of length `l cm` and cross-sectional area `A cm^(2)` is heated through `t^(@)C`. After expansion if a mechanical force is applied normal to its length on both sides of the rod and restore its original length, what is the value of force? The young's modulus of elasticity of the metal is `E` and mean coefficient of linear expansion is `alpha` per degree Celsius.
View SolutionTwo metal rods are fixed end to end between two rigid supports as shown in figure. Each rod is of length `l` and area of cross-section is `A`. When the systeam is heated up,datermine the condition when the juncation between rods does not shift ? (`Y_(1)` and `Y_(2)` are Young's modulus of materials of rods, `alpha_(1)` and `alpha_(2)` are coefficients of linear expansion)
_S01_022_Q01.png)
View SolutionA bimetallic strip of thickness `2 cm` consists of zinc and silver rivetted together. The approximate radium of curvature of the strip when heated through `50^(0)C` will be : (linear expansivity of zinc and silver are `32 xx 10^(-6//@)C` and `19 xx 10^(-6//@)C` respectively)
View SolutionA steel rail `30m` long is firmly attached to the road be only at its ends. The sun raises the temperature of the rail by `50^(0)C`, causing the rail to buckle. Assuming that the buckled rail consitst of two straight parts metting in the centre, calculate how much the centre of the rail rise? Given, `alpha_(steel) = 12 xx 10^(-6//@)C.
_S01_024_Q01.png)
View SolutionWhen composite rod is free, composite rod is free, compositive length increase to `2.002m` from temprature `20^(@)C` to `120^(@)C`. When composite rod is fixed between the support. There is no change in component length. Find `Y` and `alpha` of steel if
`Y_(cu) = 1.5 xx 10^(13 N//m^(2) alpha_(cu) = 1.6 xx 10^(-5//@)C`
_S01_025_Q01.png)
View SolutionA metal rod of Young's modulas `F` and coefficient of thermal expansion `alpha` is held at its two ends such that its length remians invariant. If its temperature is raised by `t^(@)c`, then the linear stress developed in it is
View SolutionAn aluminium sphere of `20cm` diameter is headed from `0^(@)C` to `100^(@)c`. Its volume changes by (given that the coefficient of linear expanison for aluminium `(alpha_(Al) = 23 xx 10^(-6//0)C)`
View SolutionA wooden wheel of radius R is made of two semicircular part . The two parts are held together by a ring made of a metal strip of cross sectional area S and length L. L is slightly less than `2piR`. To fit the ring on the wheel, it is heated so that its temperature rises by `DeltaT`and it just steps over the wheel. As it cools down to surrounding temperature, it process the semicircle parts together. If the coefficient of linear expansion of the metal is `alpha`, and it Young's modulus is Y, the force that one part of the wheel applies on the other part is :

View SolutionVolume of the bulb of a mercury thermometer at `0^(@)C` is `V_(@)` and area of cross section of the capillary tube is `A_(0)`, coefficient of linear expansion of glass is `alpha_(g)`, and the cubical expansion of mercury is `gamma_(m)`. If the mercury fills the bulb at `0^(@)C`, find the length of mercury column in thermometer at `T^(@)C`
View SolutionA block flats in water at `4^(0)C` so that `0.984` of its height is under water. At what temperature of water will the block just sink in water? Negleact expansion of block.
`(gamma_(R ) "for water"=2.1xx10^(-4)//^(0)C)`
View SolutionA sphete of deamrter 7.0 cm and mass 266.5 g float in a bath of liquid. As the temperature is raised, the sphere begins to sink at a temperature of `35^@ C`. If the density of liqued is `1.527 g cm^(-3)` at` 0^@C`, find the coeffiecient of cubical expamsion of the liquid. Neglect the expansion of the sphere.
View SolutionA long cylindrical metal vessel, having a linear coefficient `(alpha)`, is filled with a liquuid upto a certain level. On heating it, it is found that the level of liquid in the cylinder reamains the same. What is the cylinder reamains the same. What is the volume coefficient of expansion of the liquid?
View SolutionA `250cm^3` glass bottle is completely filled with water at `50^@C`. The bottle and water are heated to `60^@C`. How much water runs over if:
a. the expansion of the bottle is neglected:
b. the expansion of the bottle is included? Given the coefficient of areal expansion of glass `beta=1.2xx10^(-5)//K` and `gamma_("water")=60xx10^(-5)//^@C`.
View SolutionA cube of coefficient of linear expansion `alpah` is floating in a bath containing a liquid of coefficeient of volume expansion `gamma_(l)`. When the temperature is raised by `DeltaT`, the depth upto which the cube is submerged in the liquid remains the same. Find relation between `alpha` and `gamma_(l)`
View SolutionThe loss of weight of a solid when immersed in a liquid at `0^(0)C` is `DeltaW_(0)`. If `alpha` and `beta` are the volume coefficients of expansion of the solid and the liquid respectively, then the loss of weight at `t^(@)C` is approxumately
View SolutionA solid whose volume does not change with temperature floats in a liquid. For two different temperatures `t_1` and `t_2` of the liqiud, fraction `f_1` and `f_2` of the volume of the solid remain submerged in the liquid. The coefficient of volume expansion of the liquid is equal to
View SolutionA peiece of metal weight `45g` in air and `25g` `30^(@)C`. When the temperature of the liquide raised to `40^(@)`
View SolutionA Barometer with brass scale, which is correct at `0^(@)C`, reads `75cm` on a day when the air temperature is `20^(@)C`. Calculate correct reading at `0^(@)C`. (Coefficient of real expansion of mercury `=0.00018//^(@)C` and coefficient of linear expansion of brass `=0.000189//^(@)C`.)
View SolutionA given mass of ideal gas has volume `V` at pressure `P` and room temperature `T`. Its pressure is first increased by `50%` and then decreased by `50%` (both at constant temperature). The volume becomes
View SolutionThe volume of an air bubble increases by `x%` as it raises from the bottom of a water lake to its surface. If the water barometer reads `H`, the depth of the lake is
View SolutionThe density of an air bubble decrease by `x%` as it raises from the bottom of a lake to tis surface. The water berometer reads `H`. The depth of lake is
View SolutionAn ideal gas is trapped between a mercury column and the closed-end of a narrow vertical tube of uniform base containing the column. The upper end of the tube is open to the atmosphere. The atmospheric pressure equals `76cm` of mercury. The lenghts of the mercury column and the trapped air column are `20cm` and `43cm` respectively. What will be the length of the air column when the tube is tilted slowly in a vertical plane through an angle of `60^(@)`? Assume the temperature to remain constant.
View SolutionA column of mercury of 10cm length is contained in the middle of a narrow horizontal 1m long tube which is closed at both the ends. Both the halves of the tube contain air at a pressure of 76 cm of mercury. By what distance will the column of mercury be displaced if the tube is held vertically?
View SolutionA vertical cylinder of height `100cm` contains air at a constant temperature. The top is closed by a frictionless light piston. The atmospheric pressure is equal to `75cm` of mercury. Mercury is slowly poured over the piston.Find the maximum height of the mercury column that can be put on the piston.
View SolutionA gas is enclosed in a vessel of volume `V` at a pressure `P`. It is being pumped out of the vessel by mean of a piston-pump with a stroke volume. `v`. What is the final pressure in the vessel after `'n'` strokes of the pump ? Assume temperature reamains constant.
View SolutionTwo cylinder having `m_(1)g` and `m_(2)g` of a gas at pressure `P_(1)` and `P_(2)` respectively are put in cummunication with each other, temperature remaining constant. The common pressure reached will be
View SolutionIsothermal curves for a given mass of gas are shown at two different temperture `T_(1) and T_(2)` in Fig. State whether `T_(1) gt T_(2) or T_(2)gt T_(1)`. Justify your answer.
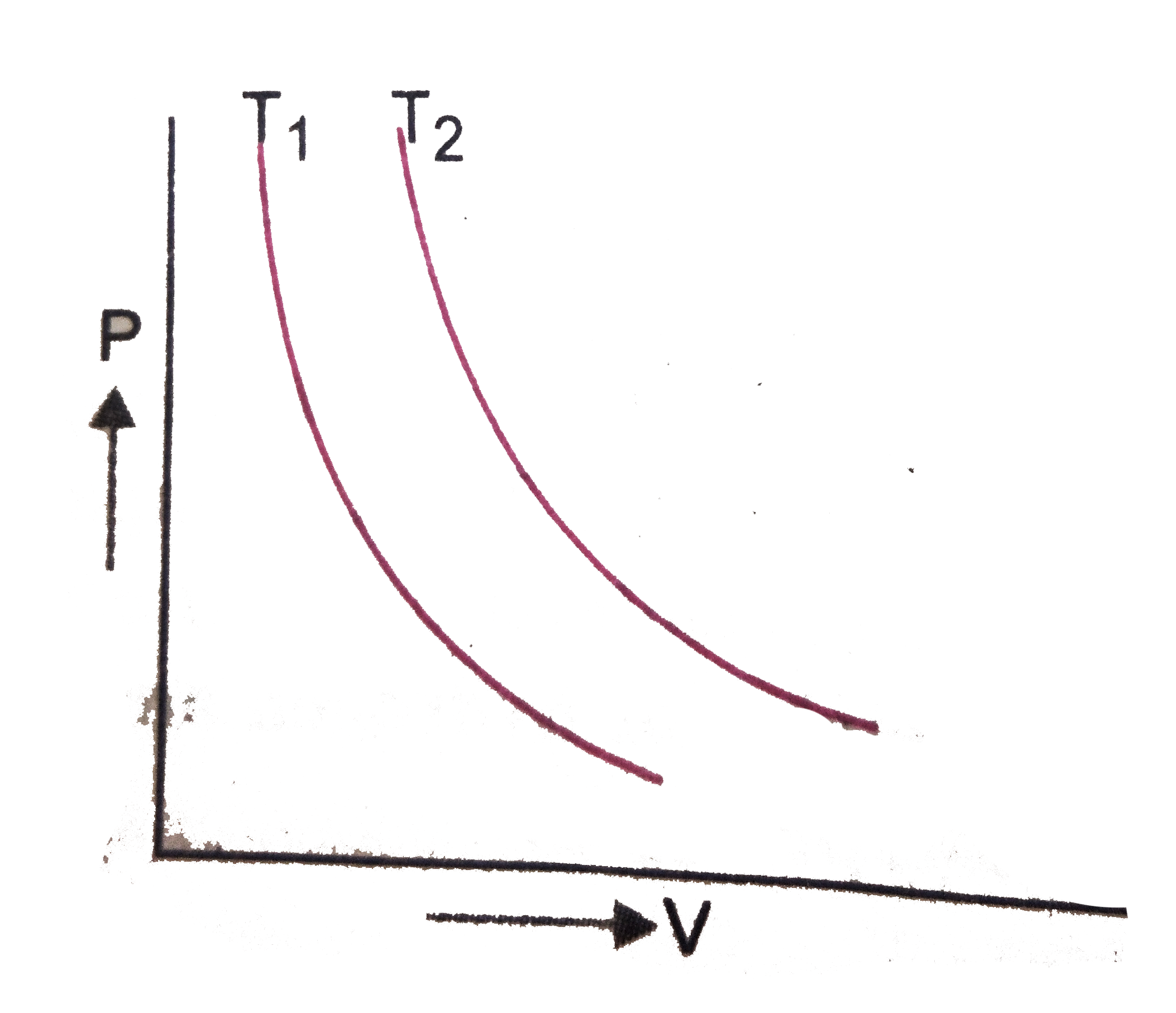
View Solution`4 g` hydrogen is mixed with 11.2 litre of He at (STP) in a container of volume 20 litre. If the final temperature is `300 K`, find the pressure.
View SolutionAn air bubble starts rising from the bottom of a lake. Its diameter is ` 3.6 mm` at the bottom and `4 mm` at the surface. The depth of the lake is `250 cm` and the temperature at the surface is `40^@ C`. What is the temperature at the bottom of the lake? Given atmospheric pressure = `76 cm of Hg and g = 980 cm//s^2`.
View SolutionA faulty barometer tube is `90cm` long and its contains some air above mercury. The reading is cm when the true atmospheric pressure `76cm`. What will be the true atmospheric pressure if the reading on this barometer is 74 cm? (H = 10cm of water column)
View Solution
Examples questions and complete solutions for chapter THERMAL PROPERTIES OF MATTER of NARAYANA PHYSICS (HINGLISH) of Class 11