Complete Solutions to LEVEL-III(C.W) of chapter KINETIC THEORY OF GASES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINETIC THEORY OF GASES |
| NARAYANA | LEVEL-III(C.W) |
| Number Of Questions | 52 |
| Academic Year | 2023-24 |
An ice block is projected vertically up with a velocity 20 `ms^(-1)`. The amount of ice that melt when it reaches the ground and if the loss of P.E. is converted into heat energy if the mass of ice block is 4.2 kg
View SolutionHow much will the temperature of 100g of water be rised by doing 4200 J of work in stirring the water?
View SolutionA lead ball moving with a velocity v strikes a wall and stops. If 50% of its energy is onverted into heat. The increase in temperature is (Specific heat of lead is S)
View SolutionA steel drill is making 180 revolution per minute, under a constant forque of 5N-m. If it drills a hole in 7sec in a steel block of mass 600gm, rise in temperature of the block is `(S=0.1 gm^(-1).^(@)C^(-1))`
View SolutionThe time taken by an electric heater to rise the temperature of 100cc of water through `10^(@)C` is 7s. If there is no loss in energy. Power of that motor is (J=4.2J/cal)
View SolutionWhen 1 gm of water changes from liquid to vapour phase at constant pressure of 1 atmosphre, the volume increases from 1cc to 1671cc. The heat of vaporisation at his pressure is 540 cal/gm. Increase in internal energy of water is (1 atmosphre =1.01x `10^(6)` dyne/`cm^(2)`)
View SolutionOne cubic meter of an ideal gas ia at a pressure at `10^(5)N//m^(2)` and temperature 300K. The gas is allowed to expand at constant pressure to twice its volume by supplying heat. If the change in internal energy in this process is `10^(4)J`, then the heat supplied is
View SolutionWhen unit mass of water boils to become steam at `100^(@)C`, it absorbs Q amount of heat. The densities of water and steam at `100^(@)C` are `rho_(1)` and `rho_(2)` respectively and the atmospheric pressure is `P_(0)`. The increase in internal energy of the water is
View SolutionConsider the melting of 1g of ice at `0^(@)C` to was at `0^(@)C` at atmospheric pressure. Then the change in internal energy of the system (density of ice is 920kg/`m^(3)`)?
View SolutionThe equation of state for a gas is given by `PV = eta RT + alpha V`, where `eta` is the number of moles and `alpha` a positive constant. The intinal pressure and temperature of 1 mol of the gas contained in a cylinder is `P_(0)` and `T_(0)`, respectively. The work done by the gas when its temperature doubles isobarically will be
View SolutionAn ideal monoatomic gas is confined in a cylinder by a spring-loaded piston of cross-section `8.0xx10^-3m^2`. Initially the gas is at 300K and occupies a volume of `2.4xx10^-3m^3` and the spring is in its relaxed (unstretched, unompressed) state, fig. The gas is heated by a small electric heater until the piston moves out slowly by 0.1m. Calculate the final temperature of the gas and the heat supplied (in joules) by the heater. The force constant of the spring is `8000 N//m`, atmospheric pressure is `1.0xx10^5 Nm^-2`. The cylinder and the piston are thermally insulated. The piston is massless and there is no friction between the piston and the cylinder. Neglect heat loss through lead wires of the heater. The heat capacity of the heater coil is negligible. Assume the spring to be massless.

View Solution`A` cylinder of fixed capacity `67.2` liters contains helium gas at `STP` . Calculate the amount of heat required to rise the temperature of the gas by `15^(@)C` ? `(R=8.314 J mol^(-1)k^(-1))`
View Solution`14 g of N_(2)` gas is heated in a closed rigid container to increase its temperature from `23^(@)C` to `43^(@)C`. The amount of heat supplied to the gas is
View Solution70 calories of heat required to raise the temperature of 2 moles of an ideal gas at constant pressure from `30^@Cto 35^@C.` The amount of heat required (in calories) to raise the temperature of the same gas through the same range `(30^@C to 35^@C)` at constant volume is:
View SolutionThe relation between internal energy `U`, pressure `P` and volume `V` of a gas in an adiabatic process is
`U = a + bPV` where a and b are constants. What is the effective value of adiabatic constant `gamma` ?
View SolutionIf the ratio of specific heat of a gas of constant pressure to that at constant volume is `gamma`, the change in internal energy of the mass of gas, when the volume changes from `V` to `2V` at constant pressure `p` is
View SolutionAn ideal gas at `27^(@)C` is compressed adiabatically to `8//27` of its original volume. If `gamma = 5//3`, then the rise in temperature is
View SolutionOne mole of a gas expands with temperature T such thaht its volume, V=`KT^(2)`, where K is a constant. If the temperature of the gas changes by `60^(@)C` then the work done by the gas is `120R
View SolutionA monoatomic ideal gas, initially at temperature `T_1,` is enclosed in a cylinder fitted with a friction less piston. The gas is allowed to expand adiabatically to a temperature `T_2` by releasing the piston suddenly. If `L_1 and L_2` are the length of the gas column before expansion respectively, then `(T_1)/(T_2)` is given by
View SolutionThree samples of the same gas 'x','y' and 'z', for which the ratio of specific heats in `gamma=3//2`, have initially the same volume. The volumes of each sample is doubled, by adiabatic process in the case of 'x' by isobaric process in the case of 'y' and by isothermal process in the case of 'z'. If the initial pressures of the samples 'x','y' and 'z' are in the ratio `2sqrt(2):1:2`, then the ratio of theri final pressures is
View Solutionn moles of an ideal gas undergo a process in which the temperature changes with volume as `T=kv^(2)`. The work done by the gas as the temperature changes from `7_(0)` to `47_(0)` is
View Solutionm' grams of a gas of a molecular weight M is flowing in a isolated tube with velocity 2v. If the gas flow is suddenly stopped the rise in its temperature is (`gamma=` ratio of specific heats, R=universal gas constant, J=Mechanical equivalent of heat)
View SolutionHeat is supplied to a diatomic gas at constant pressure.
The ratio of `DeltaQ : DeltaU : DeltaW` is
View SolutionA given quantity of an ideal gas at pressure P and absolute temperature T obyes `P alpha T^(3)` during adiabatic process. The adiabatic bulk modulus of the gas is
View SolutionAn ideal gas is taken through a cyclic thermodynamic process through four steps. The amounts of heat involved in these steps are `Q_1=5960J, Q_2=-5585J, Q_3=-2980J and Q_4=3645J`, respectively. The corresponding quantities of work involved are `W_1=2200J, W_2=-825J, W_3=-1100J and W_4` respectively.
(1) Find the value of `W_4`.
(2) What is the efficiency of the cycle
View SolutionDuring an adibatic compression ,830 J of work is done on 2 moles of a diatomic ideal gas to reduce its volume by 50%. The change in its temperature is nearly:
View SolutionConsider a spherical shell of radius R at temperature T. The black body radiation inside it can be considered as an ideal gas of photons with internal energy per unit volume `u=U/V propT^4` and pressure `P=1/3(U/V)`. If the shell now undergoes an adiabatic expansion the relation between T and R is :
View SolutionAn ideal gas under goes a quasi static, reversible process in which its molar heat capacity C remains constant. If during this process the relation of pressure P and volume V is given by `PV^n=constant`, then n is given by (Here `C_P and C_V` are molar specific heat at constant pressure and constant volume, respectively):
View Solutionn' moles of an ideal gas undergoes a process `AtoB` as shown in the figure. The maximum temperature of the gas during the process will be:
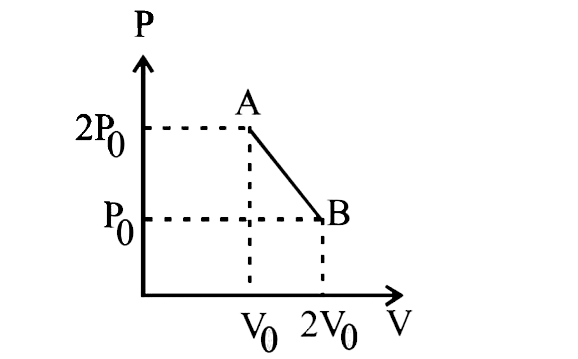
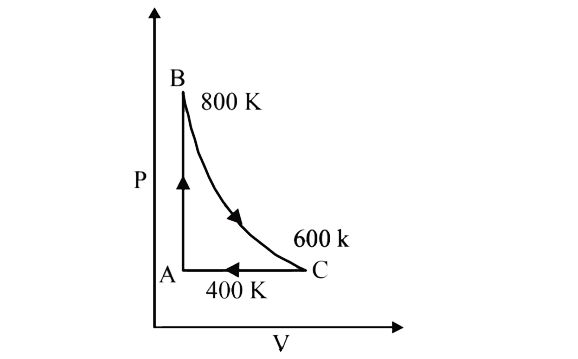
View SolutionOne mole of a diatomic ideal gas undergoes a cyclic process ABC as shown in figure. The process BC is adiabatic. The temperature at A,B and C are 400K, 800K and 600K respectively. Choose the correct statement:
View SolutionConsider an ideal gas confined in an isolated closed chamber. As the gas undergoes an adiabatic expansion, the average time of collision between molecules increase as `V^q`, where V is the volume of the gas. The value of q is : `(gamma=(C_p)/(C_v))`
View SolutionAn ideal gas goes through a reversible cycle `ararrBrarrcrarrd` has the V-T diagram shown below. Process `drarra` and `brarrc` are adiabatic
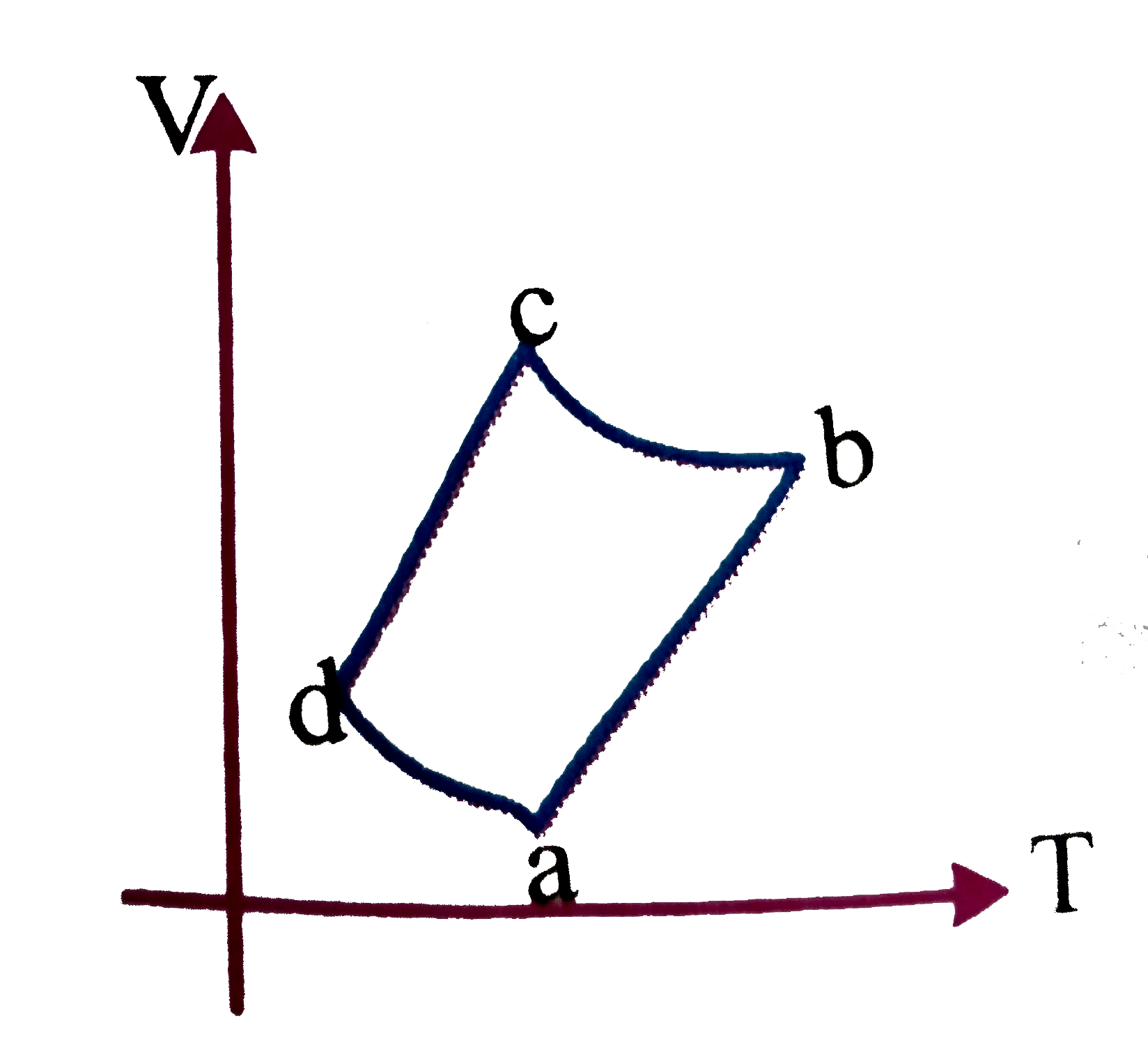
The corresponding P-V diagram for the process is(all figures are schematic and not drawn to scale)
View SolutionA Carnot's engine is made to work between `200^(@)C` and `0^(@)C` first and then between `0^(@)C` and `-200^(@)C`. The ratio of efficiencies of the engine in the two cases is
View SolutionA scientist says that the efficiency of his heat engine which operates at source temperature `127^(@)C` and sink temperature `27^(@)C is 26%`, then
View SolutionEfficiency of a Carnot engine is `50%` when temperature of outlet is `500 K`. In order to increase efficiency up to `60%` keeping temperature of intake the same what is temperature of outlet?
View SolutionAn ideal refrigerator has a freezer at a temperature of `-13^(@)C`. The coefficient of performance of the engine is `5`. The temperature of the air (to which heat is rejected) will be
View SolutionThe heat reservoir of an ideal carnot engine is at 800K and its sink is at 400K. The amount of heat taken in it in one second to produce useful mechanical work at the rate of 750J is
View SolutionA Carnot engine workds between `200^(@)C` and `0^(@)C` and `.-200^(@)C`. In both caes the working substance absorbes 4 kilocalories of heat from the source. The efficiency of first engine will be
View SolutionIn the above problem, the output of second engine is
View SolutionIn the above problem, the ratio of outputs of two engines is
View SolutionA carbot freezer takes heat from water at `0^(@)C` inside it and rejects it to the room at a temperature of `27^(@)C`. The latent heat of ice is `336xx10^(3)Jkg^(-1)`. If 5kg of water at `0^(@)C` is converted into ice at `0^(@)C` by the freezer, then the enrgy consummed by the freezer is close to :
View SolutionA carnot engine absorbs `1000J` of heat energy from a reservoir at `127^(@)C` and rejecs `600J` of heat energy during each cycle. Calculate (i) efficiency of the engine, (ii) temperature of sink, (iii) amount of useful work done per cycle.
View SolutionAn ideal monoatomic gas is taken round the cycle ABCDA as shown in the P-V diagram. The work done during the cycle is
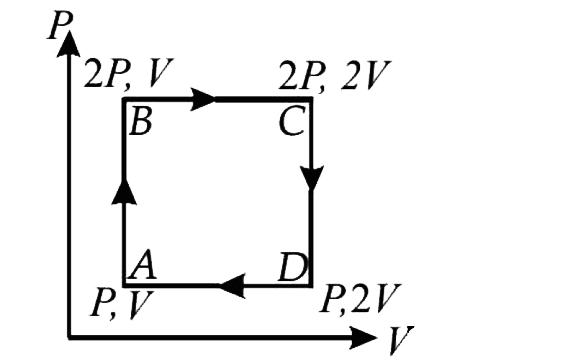
View SolutionThe figure shows P-V graph of an ideal on molegas undergone to cyclic process ABCD then the process `BrarrC` is
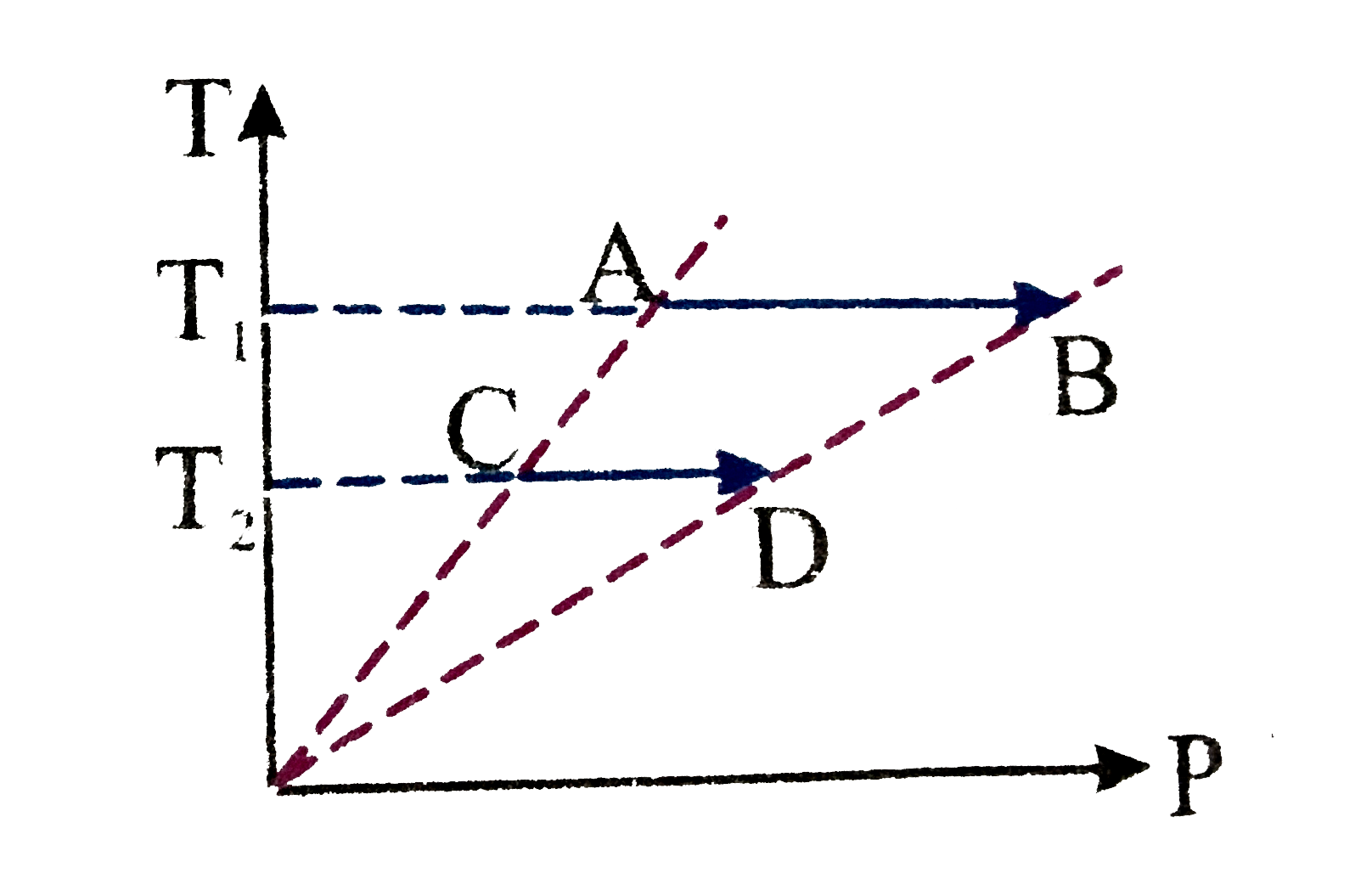
View SolutionOn a T-P diagram, two moles of ideal gas perform process AB and CD. If the work done by the gas in the process AB is two times the work done in the process CD then what is the value of `T_(1)/T_(2)`?
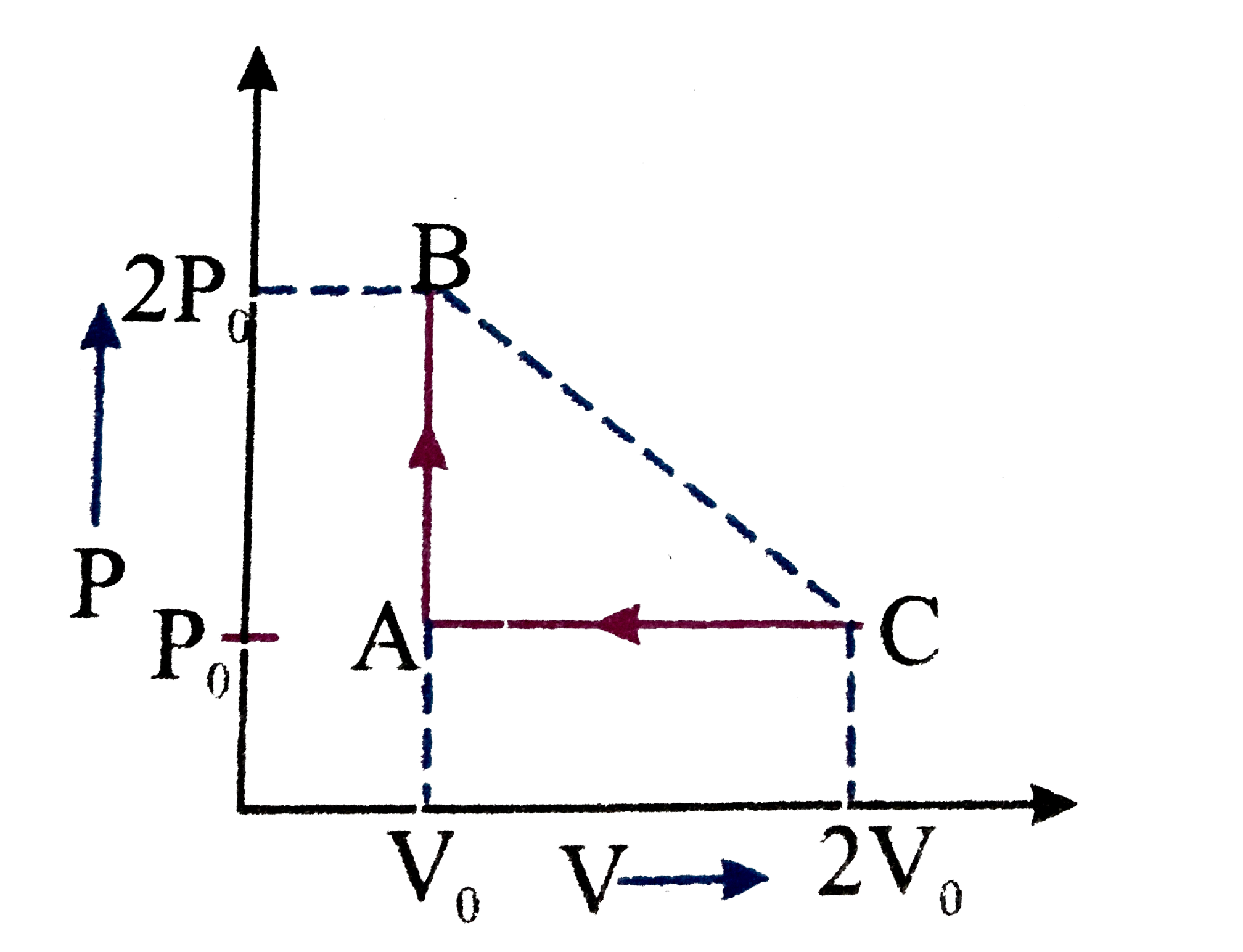
View SolutionA sample of an ideal monoatomic gas is taken round the cycle ABCA as shown in the figure the work done during the cycle is

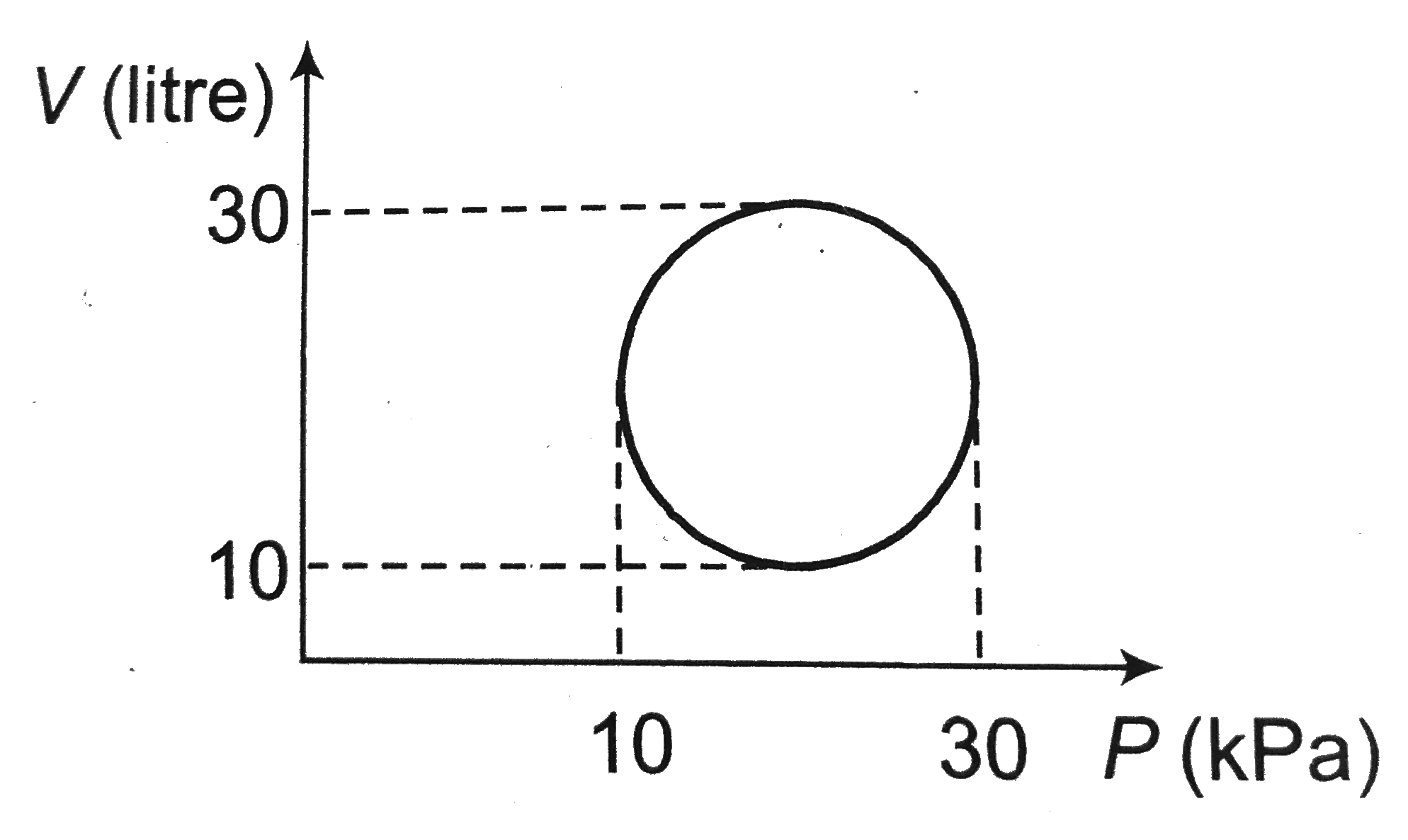
View SolutionIn the given elliptical `P-V` diagram
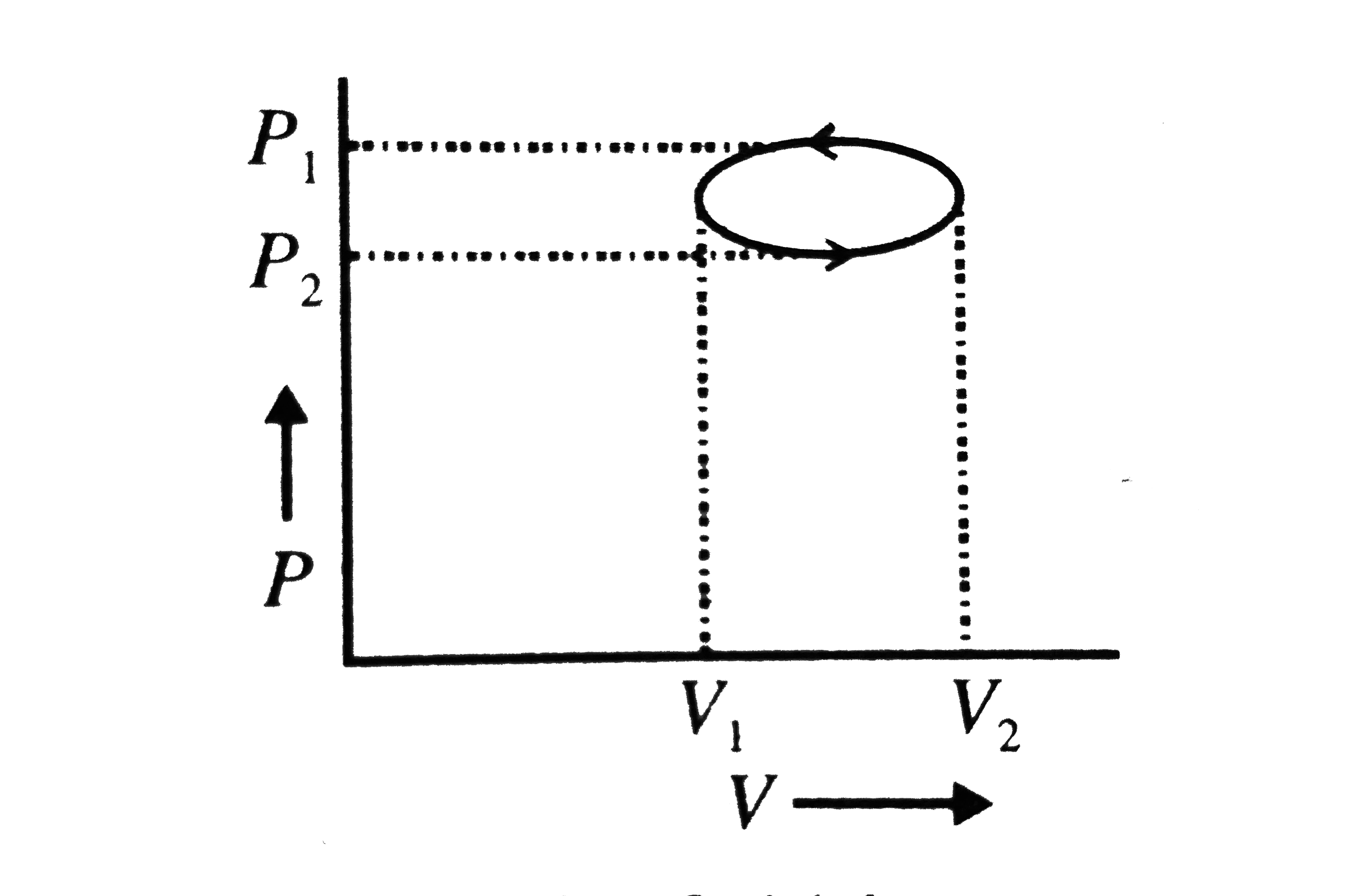
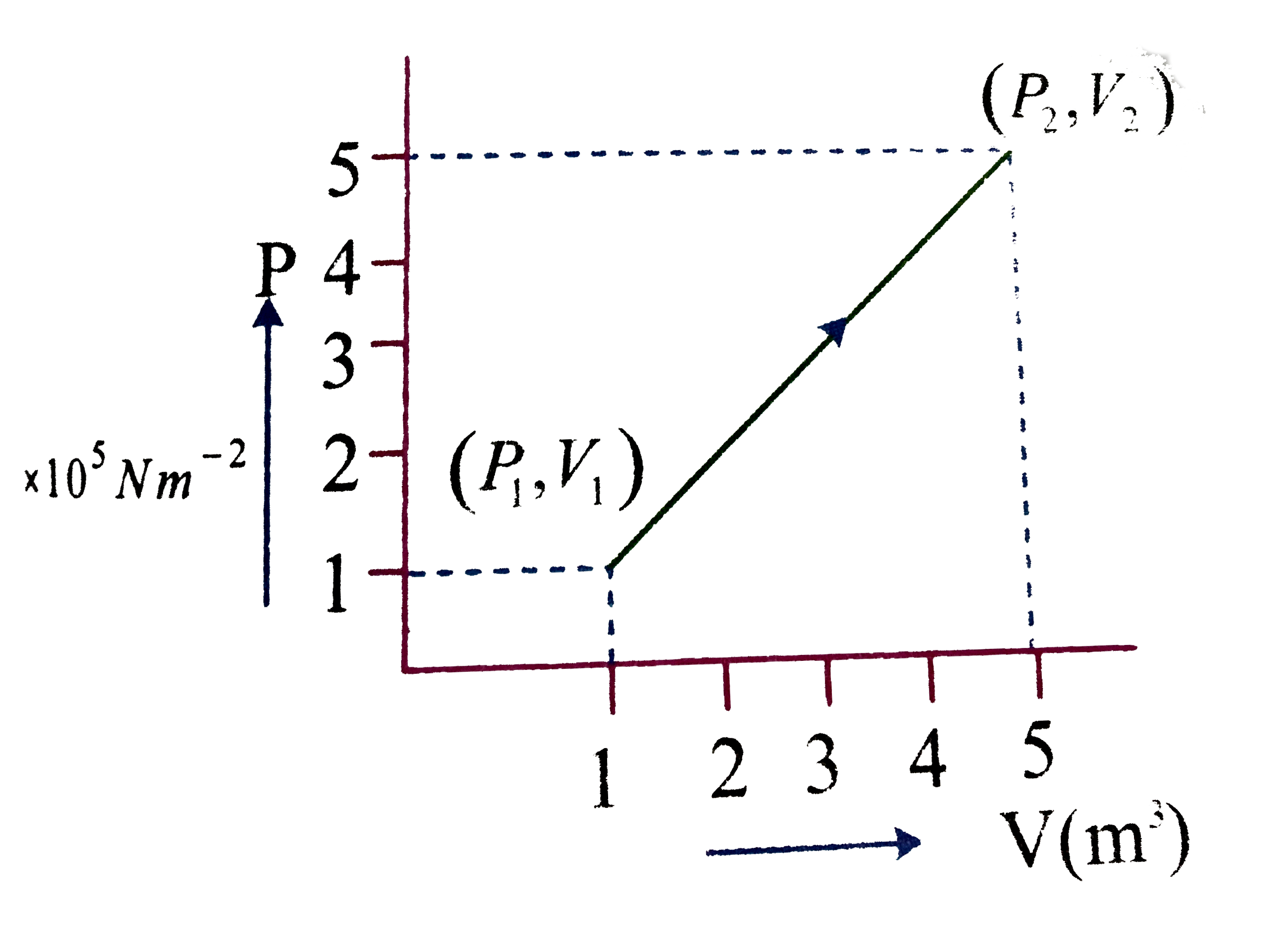
View SolutionA system changes from the state `(P_(1),V_(1))` to `(P_(2)V_(2))` as shwon in the diagram. The workdone by the system is
View SolutionHeat energy abosrbed by a system in going through a cyclic process shown in figure is
View SolutionA thermodynamic system is taken through the cyclic `PQRSP` process. The net work done by the system is

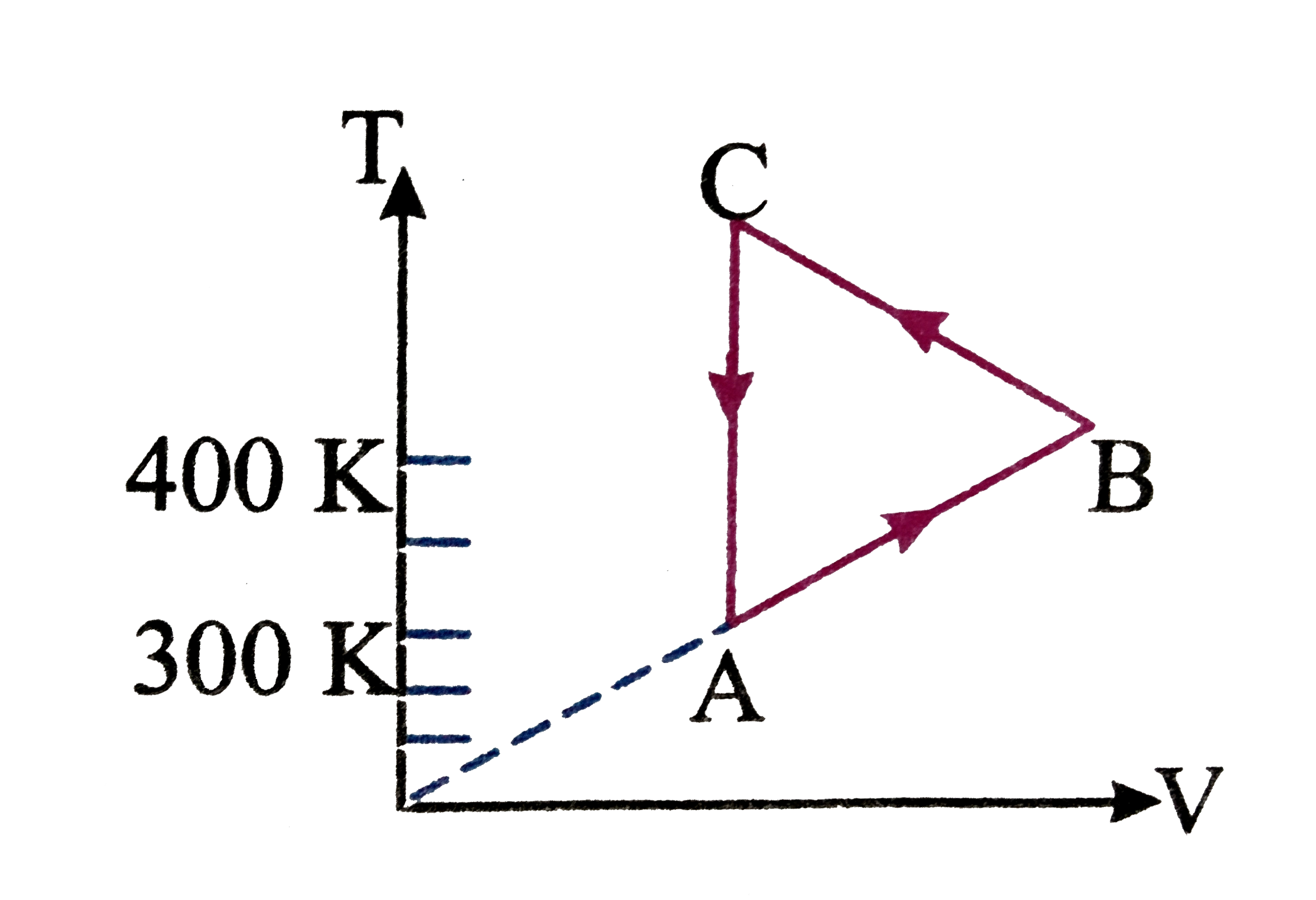
View SolutionA cyclic process performed on one mole of an ideal gas. A total 1000 J of heat is withdrawn from the gas in a complete cycle. Find the work. Done by the gas druing the process `BrarrC`.
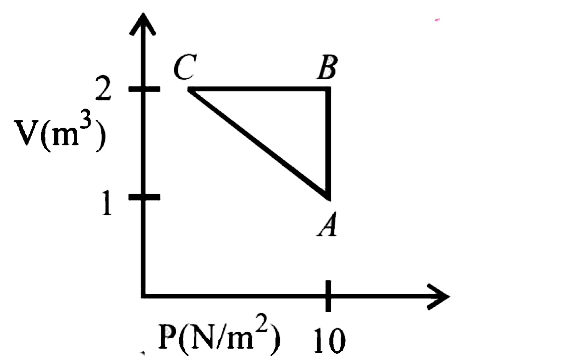
View SolutionAn ideal gas is taken through the cycle `AtoBtoCtoA,` as shown in the figure, If the net heat supplied to the gas in the cycle is 5J, the work done by the gas in the process CtoA is
View Solution
LEVEL-III(C.W) questions and complete solutions for chapter KINETIC THEORY OF GASES of NARAYANA PHYSICS (HINGLISH) of Class 11