Complete Solutions to SOLVED EXAMPLE of chapter KINETIC THEORY OF GASES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINETIC THEORY OF GASES |
| NARAYANA | SOLVED EXAMPLE |
| Number Of Questions | 83 |
| Academic Year | 2023-24 |
Fig shows of `PV//T` versus P for `1.00 xx 10^(-3) kg` of oxygen gas at two different temperatures.
(a) What does the dotted plot signify ?
(b) Which is true : `T_(1) lt T_(2) or T_(2) lt T_(1) ?`
( c) What is the value of `PV//T` where the curves meet on the Y-axis ?
(d) If we obtained similar plot for `1.00 xx 10^(-3) kg` of hydrogen, would we get the same value of `PV//T` at the point where the curves meet on the y-axis ? If not, what mass of hydrogen yield the same value of `PV//T` (for low pressure high temperature region of the plot) ? (Molecular mass of `H = 2.02 u`, of `O = 32.0 u, R = 8.31 J "mol"^(-1) K^(-1)`

View SolutionA vessel contains two non-reactive gases neon (monoatomic) and oxygen (diatomic). The ratio of their partial pressures is 3:2. Estimate the ratio of
(i) number of molecules, and
(ii) mass density of neon and oxygen in the vessel.
Atomic mass of neon = 20.2 u, and molecular mass of oxygen = 32.0 u.
View SolutionThe total number of air molecules in a room of capacity `20 m^(3)` at a temperature of `27^(@)C` and 1 atm pressure is
View SolutionA vessel is filled with a gas at a pressure of 76 cm of mercury at a certain temperature. The mass of the gas is increased by 50% by introducing more gas in the vessel at the same temperature. Find the resultant pressure of the gas.
View SolutionWhat is the total kinetic energy of 2g of Nitrogen gas at temperature 300K.
View SolutionYour are given the following group of particles, `n_(i)` represents the number of molecules with speed `v_(i)`
`(P_(2))/(P_(1))=(m_(2))/(m_(1)) : (p_(2))/(76)=(m_(1)+(50)/(100)m_(1))/(m_(1))=(3)/(2)`
calculate (i) average speed (ii) rms speed
(iii) most probable speed.
View SolutionTwo vessels have equal volums. One of them contains hydrogen at one atmosphere and the other helium at two atmosphere. If both the samples are at the same temperature, the `rms` velocity of the hydrogen molecules is
View SolutionAt what temperature , will the rms speed of oxygen molecules be sufficient for escaping from the earth ? Take `m = 2.76 xx 10^(-26) kg, k = 1.38 xx 10^(-23) J//K and v_(e) = 11.2 km//s`.
View SolutionCalculate (i) rms velocity and (ii) mean kinetic energy of one gram molecule of hydrogen at STP. Given density of hydrogen at STP is `0.09 kg m^(-3)`.
View SolutionTwo moles of an idel gas X occupying a volume V exerts a pressure P. The same pressure is exerted by one mole of another gas Y occupying a volume 2V. (if the molecular weight of Y is 16 times the molecular weight of X), find the ratio of the 'rms' speeds of the molecules of X and Y.
View SolutionThree vessel of equal capacity have gases at the same temperature and pressure. The first vessel contains neon (monoatomic), the second contains chlorine (diatomic), and the third contains uranium hexafluoride (polyatomic). Do the vessels contains equal number of respectice molecules ? Is the root mean square speed of molecules the same in the three cases ? If not, which case is `v_(rms)` the largest?
View SolutionAt what temperature is the root mean square speed of an atom in an argon gas cylinder equal to the r.m.s. speed of a helium gas atom at `-20^(@) C` ? (Atomic mass of Ar = 39.9 u, of He = 4.0 u).
View SolutionA nitrogen molecule at the surface of earth happens to have 'rms' speed for that gas at `0^(@)C`. If it were to go straight up without colliding with other molecules, how high would it rise? (Mass of nitrogen molecule, `m=4.65xx10^(-26) kg,R=8.3J//mol//K`)
View SolutionA gas mixture consists of 2 moles of oxygen and 4 moles of argon at temperature T. Neglecting all vibrational modes, the total internal energy of the system is
View SolutionOne kg of a diatomic gas is at pressure of `8xx10^4N//m^2`. The density of the gas is `4kg//m^3`. What is the energy of the gas due to its thermal motion?
View SolutionCalculate the total kinetic energy of one kilo mole of Oxygen gas at `27^(@)C`
View SolutionTwo perfect gases at absolute temperature `T_(1) and T_(2)` are mixed. There is no loss of energy. The masses of the molecules are `m_(1) and m_(2)`. The number of molecules in the gases are `n_(1) and n_(2)`. The temperature of the mixture is
View SolutionA cylinder of fixed capacity 22.4 litre contains helium gas at standard temperature and pressure. What is the amount of heavy needed to raise the temperature of the gas in the cylinder by `30^(@)C` ? `(R=8.31J "mol"^(-1)K^(-1))`
View SolutionA gas has molar heat capacity `C = 37.55 J "mole"^(-1)K^(-1)`, in the process PT = constant, find the number of degree of freedom of the molecules of the gas.
View SolutionEstimate the mean free path for a water molecule in water vapour at 373 K. Given diameter of water molecule `= 2 Å` and number density of water molecule (at NTP) `= 2.7 xx 10^(25) m^(-3)`. Compare it with interatomic distance for water `= 40 Å`.
View SolutionEstimate the mean free path and collision frequency of a nitrogen molecule in a cylinder containing nitrogen at 2 atm and temperature `17^(@) C`. Take the radius of a nitrogen molecule to be roughly `1.0 Å`. Compare the collision time with the time the molecule moves freely between two successive collisions. (Molecular mass of nitrogen = 28.0 u).
View SolutionA 10kw drilling machine is used for 5 minutes to bore a hole in an aluminium block of mass `10xx10^(3)kg`. If 40% of the work done is utilised to raise the temperature of the block, then find the raise in temperature of the aluminium block?
(Specific heat of Aluminium `=0.9 Jkg^(-1)k^(-1)`)
View SolutionHailstones fall from a certain height. If they melt completely on reaching the ground, find the height from which they fall. (`g=10ms^(-2),L=80` calorie/g and J=4.2 J/calorie.)
View SolutionA girl weighing 42 kg eats bananas whose energy is 980 calories. If this energy is used to height h find the value of h. (J=4.2J calorie)
View SolutionA lead bullet of mass 21g travelling at a speed of 100 `ms^(-1)` comes to rest in a wooden block. If no heat is taken away by the wood, the rise in temperature of the bullet in the wood nearly is (Sp. Heat of lead 80cal/kg `.^(@)C`)
View SolutionThe height of Niagra falls is 50 m. Calculate the difference in temperature of water at the top and at the bottom of fall, if `J = 4.2 J cal^(-1)`.
View SolutionA piece of ice at `0^(@)C` falls from rest into a take of water which is also at `0^(@)C` and 0.5% of ice melts. Find the minimum height from which the ice falls.
View SolutionWhen heat energy of 1500J is supplied to a gas the external workdone by the gas is 525J what is the increase in its internal energy
View Solution`1gm` water at `100^(@)C` is heated to convert into steam at `100^(@)C` at `1atm`. Find out chage in internal energy of water. It is given that volume of `1gm` water at `100^(@)C = 1c c`, volume of `1gm` steam at `100^(@)C = 167 1 c c`. Latent heat of vaporization `= 540 cal//g`. (Mechanical equivalent of heat `J = 4.2J//cal)`
View SolutionCalculate the external workdone by the system in Kcal, when 40 Kcal of heat is supplied to the system and internal energy rises by 8400J.
View SolutionIn a thermodynamic process, pressure of a fixed mass of a gas is changed in such a manner that the gas release `20 J` of heat and `8 J` of work is done on the gas. If initial internal energy of the gas was `30 J`, what will be the final internal energy?
View SolutionConsider the vaporization of 1g of water at `100^(@)C` at one atmosphere pressure. Compute the work done by the water system in the vaporization and change internal energy of the system.
View SolutionCalculate difference in specific heats for `1` gram of air at `N.T.P`. Given density of air at N.T.P. is `1.293 g litre^(-1), j=4.2xx10^(7)" erg "cal^(-1)`.
View SolutionFour moles of a perfect gas is heated to increaes its temperature by `2^(@)C` absorbs heat of 40cal at constant volume. If the same gas is heated at constant pressure find the amount of heat supplied.
View SolutionWhen an ideal diatomic gas is heated at constant pressure fraction of the heat energy supplied which increases the internal energy of the gas is
View SolutionA quantity of heat Q is supplied to a monoatomic ideal gas which expands at constant pressure. The fraction of heat that goes into work done by the gas `((W)/(Q))` is
View SolutionThe specific heat capacity of a metal at low temperature (T) is given as
`C_(p)(kJK^(-1) kg^(-1)) =32((T)/(400))^(3)`
A 100 gram vessel of this metal is to be cooled from `20^(@)K` to `4^(@)K` by a special refrigerator operating at room temperaturte `(27^(@)C)` . The amount of work required to cool the vessel is
View Solution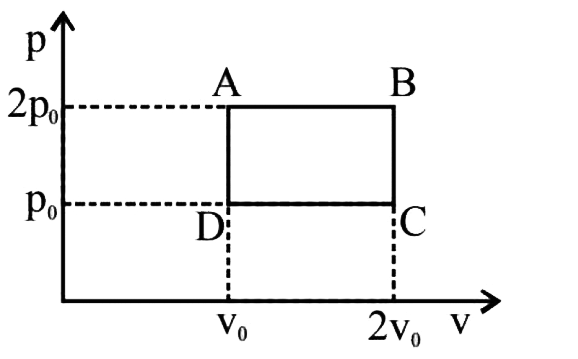
The above p-v diagram represents the thermodynamic cycle of an engine, operating with an ideal monoatomic gas. The amount of heat, extracted from the source in a single cycle is
View SolutionA piston divides a closed gas cylinder into two parts. Initially the piston is kept pressed such that one part has a pressure P and volume 5V and the other part has pressure 8P and volume V, the piston is now left free. Find the new pressure and volume for the isothermal and aidabatic process. `(gamma=1.5)`
View SolutionIn a cyclic process shown in the figure an ideal gas is adiabatically taken from `B`to`A`, the work done on the gas during the process `B`to`A` is `30,J` when the gas is taken from `A` to `B` the heat absorbed by the gas is `20 J` Then change in internal energy of the gas in the process `A` to `B` is :

View SolutionA gas undergoes a change of state during which 100J of heat is supplied to it and it does 20J of work. The system is brough back to its original state through a process during which 20 J of heat is released by the gas. What is the work done by the gas in the second process?
View SolutionAn ideal gas is taken through the cycle `AtoBtoCtoA,` as shown in the figure, If the net heat supplied to the gas in the cycle is 5J, the work done by the gas in the process CtoA is
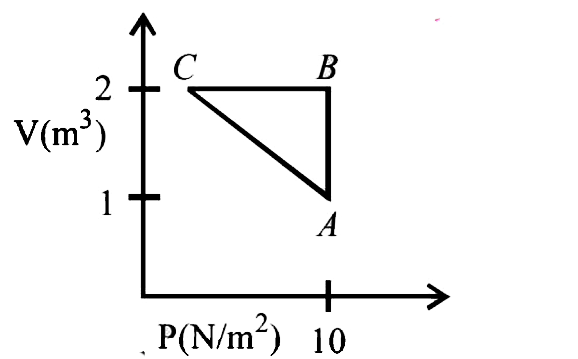
View SolutionAn ideal monoatomic gas is taken round the cycle ABCDA as shown in the P-V diagram. Compute the work done in the process.
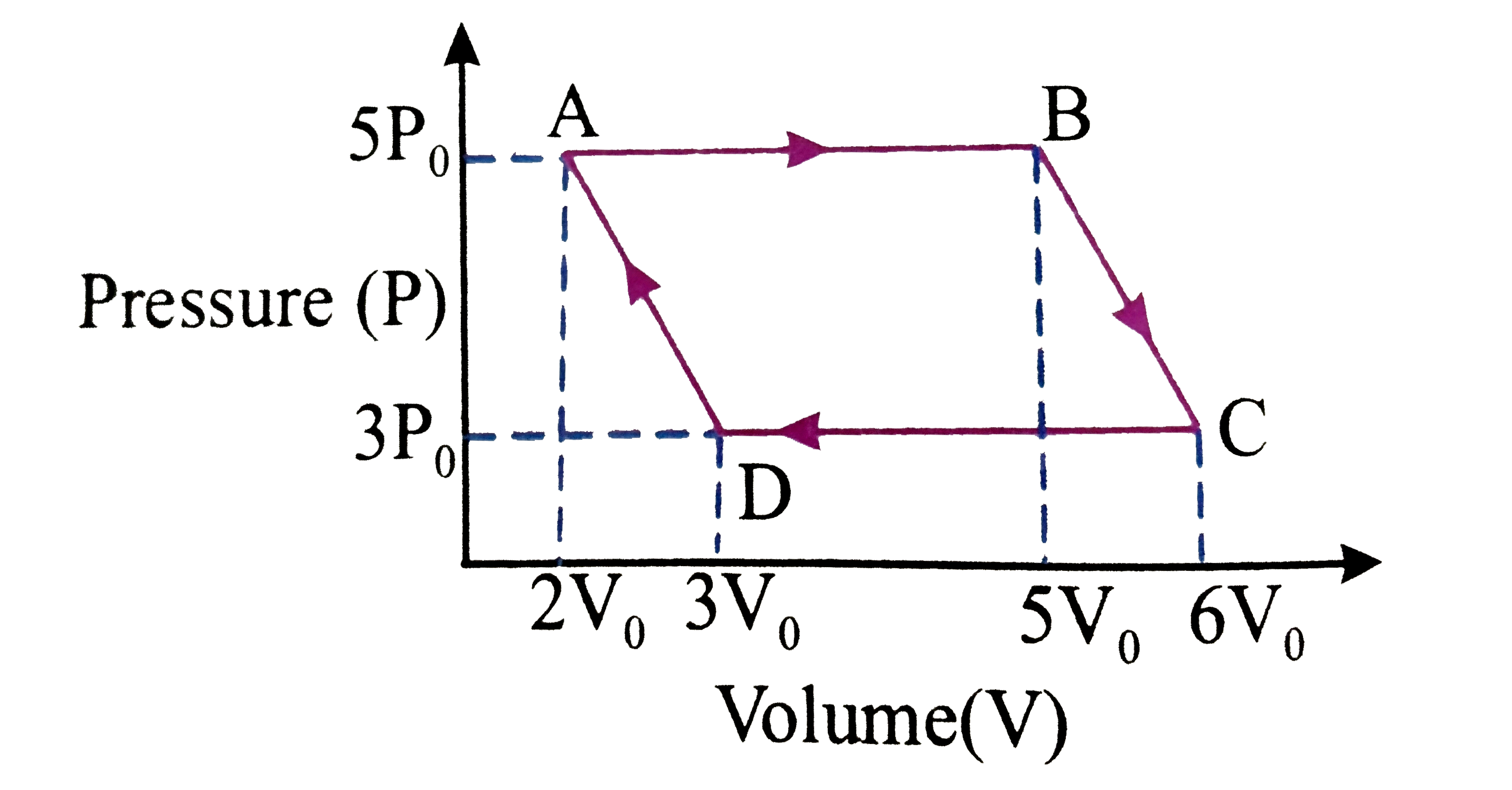
View SolutionDuring an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio `C_P//C_V` for the gas is
View SolutionWhen 5 moles of an ideal gas is compressecd isothermally, its volume decreases from 5 litre to 1 litre. If the gas is at `27^(@)C`, find the work done on the gas `("log"_(10)((1)/(5))=-0.6990)`.
View SolutionA gas is expanded to double its volume by two different processes. One is isobaric and the other is isothermal. Let `W_(1)` and `W_(2)` be the respective work done, then find `W_(1)` and `W_(2)`
View SolutionTemperature of 1 mole of an ideal gas is increased from 300K to 310K under isochoric process. Heat supplied to the gas in this process is Q=25R, where R=universal gas constant. What amount of work has to be done by the gas if temperature of the gas decreases from 310K to 300K adiabatically?
View SolutionA tyre pumped to a pressure of 6 atmosphere suddenly bursts. Room temperature is `25^(@)C`. Calculate the temperature of escaping air. `(gamma=1.4.)`
View SolutionThree samples of the same gas A,B and C `(gamma=3//2)` have initially equal volume. Now the volume of each sample is doubled. The process is adiabatic for A. Isobaric for B and isothermal for C. If the final pressures are equal for all three samples, find the ratio of their initial pressures
View SolutionAn ideal gas mixture filled inside a balloon expands according to the relation expands according to the relation `PV^(2//3)=` constant. What will be the temperature inside the balloon
View SolutionFind the amount of work done to increase the temperature of one mole jof an ideal gas by `30^(@)C`, if it is expanding under condition `VooT^(2//3)`.
View SolutionP-V diagram of a diatomic gas is a straight line passing through origin. The molar heat capacity of the gas in the process will be
View SolutionThe molar heat capacity in a process of a diatomic gas if it does a work of `Q/4` when a heat of `Q` is supplied to it is
View SolutionA monoatomic gas undergoes a process given by `2dU+3dW=0`, then what is the process
View SolutionThe relation between U, P and V for an iodeal gas is U=2+3PV. What is the atomicity of the gas.
View SolutionOne mole of a monoatomic ideal gas undergoes the process `ArarrB` in the given P-V diagram. What is the specific heat for this process?
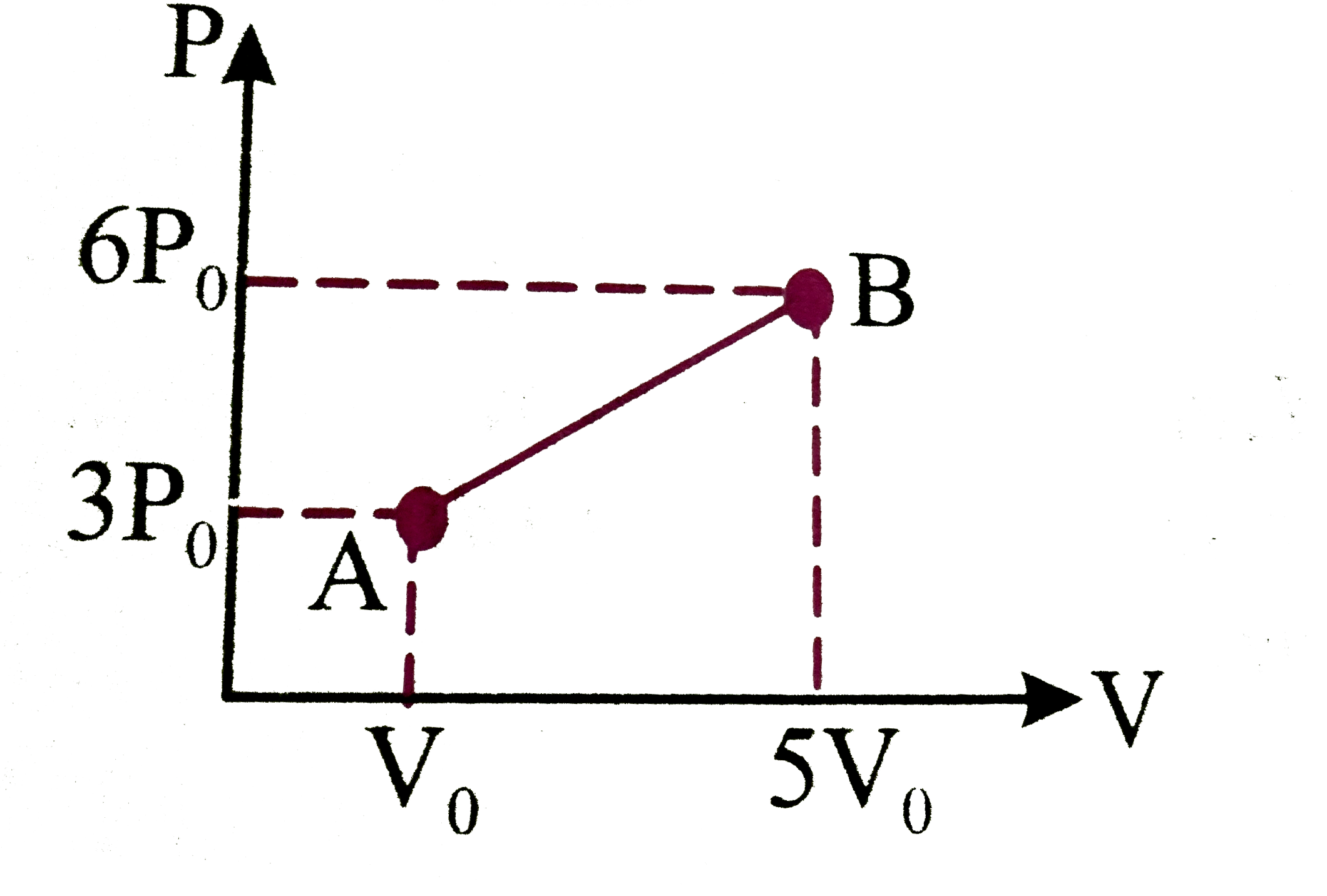
View SolutionIf `C_(P_` and `C_(v)` denote the specific heats nitrogen per unite mass at constant pressure and constant volume respectively, then
(1) `C_(P)-C_(v)=(R)/(28)` (2) `C_(P)-C_(v)=(R)/(14)`
(3) `C_(P)-C_(v)=R` (4) `C_(P)-C_(v)=28R`
View SolutionWhen a system is taken from state i to state f along the path iaf, it is found that `Q=50 cal and W=20 cal`. Along the path ibf `Q=36cal`. W along the path ibf is

View SolutionA thermally insulated vessel contains an ideal gas of molecular mass M and ratio of specific heats `gamma`. It is moving with speed v and it's suddenly brought to rest. Assuming no heat is lost to the surroundings, Its temperature increases by:
View Solution100g of water is heated from `30^@C to 50^@C`. Ignoring the slight expansion of the water, the change in its internal energy is (specific heat of water is `4184J//kg//K`):
View SolutionFive moles of hydrogen initially at STP is compressed adiabatically so that its temperature becomes 673K. The increase in internal energy of the gas, in kilo joule is (R=8.3J/molK, `gamma`=1.4 for diatomic gas)
View SolutionIf the ratio of specific heat of a gas of constant pressure to that at constant volume is `gamma`, the change in internal energy of the mass of gas, when the volume changes from `V` to `2V` at constant pressure `p` is
View SolutionThree moles of an ideal monoatomic gas undergoes a cyclic process as shown in the figure. The temperature of the gas in different states marked as 1,2,3 and 4 are 400K, by the gas during the process 1-2-3-4-1 is (universal gas constant is R)
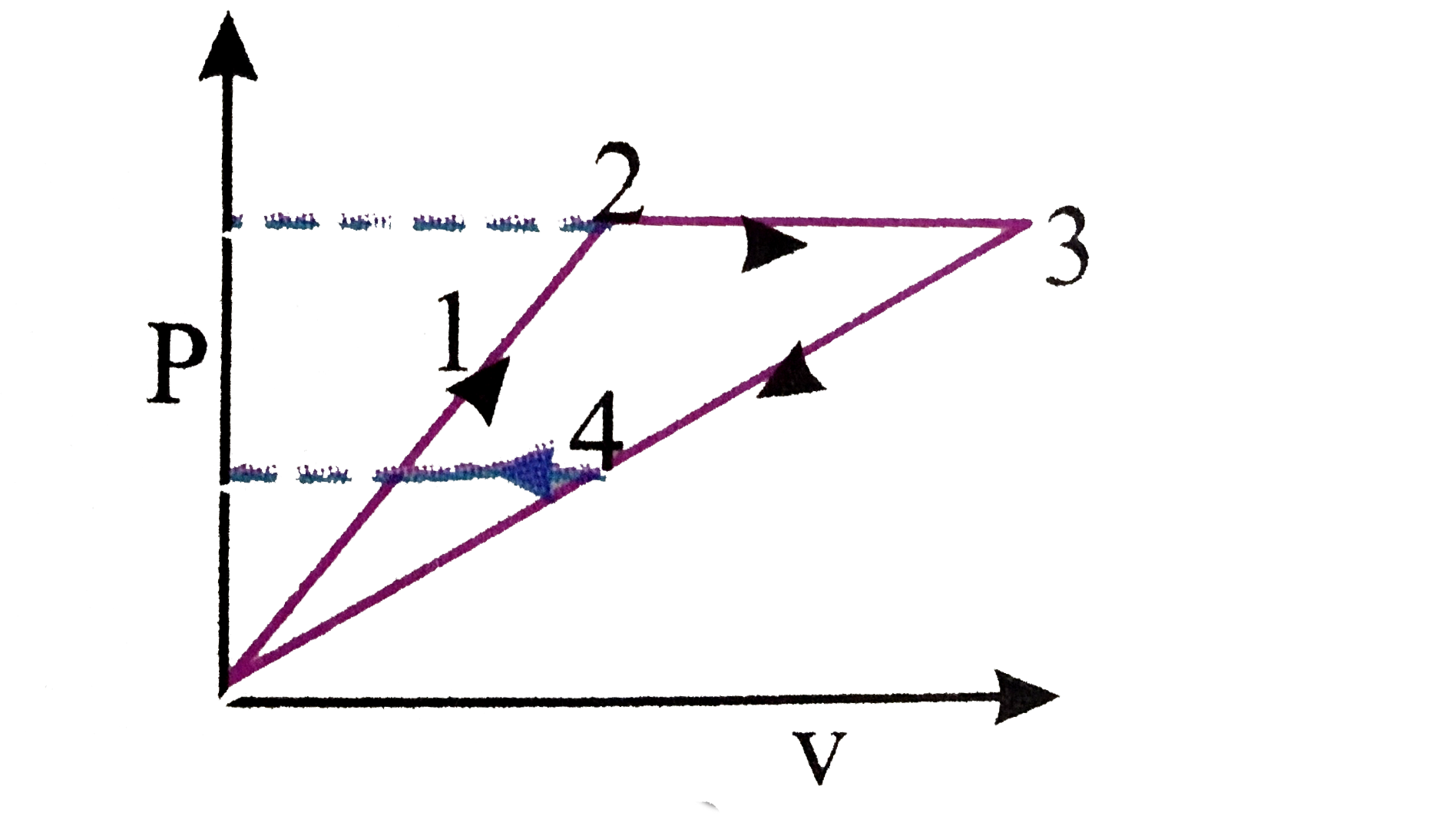
View Solution`3` moles of an ideal mono atomic gas performs a cycle as shown in fig. `If` gas temperature `T_(A)=400 K` `T_(B)=800K,T_(C)=2400K`, and `T_(D)=1200K`. Then total work done by gas is
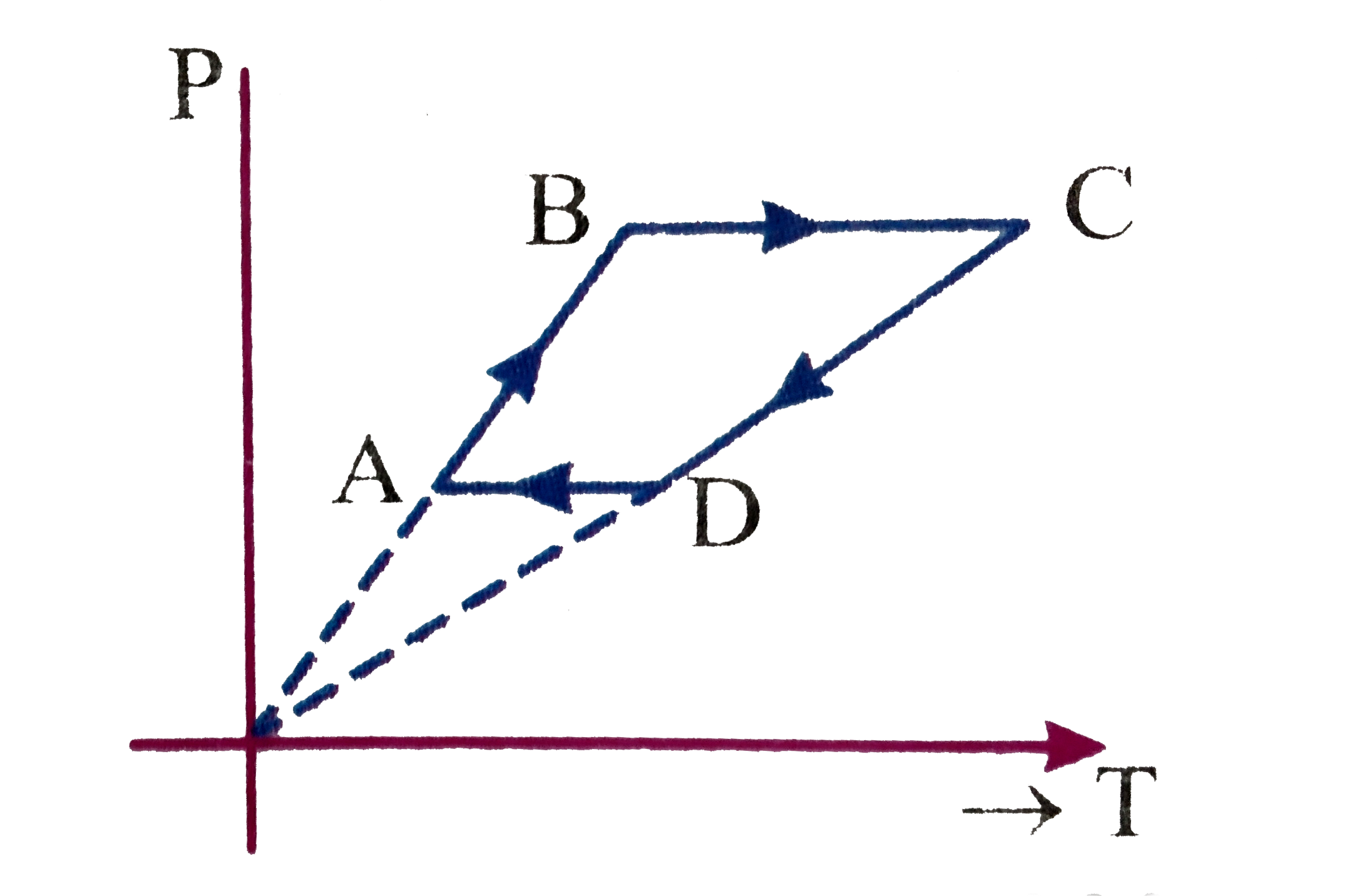
View SolutionAn ideal gas is subjected to a cyclic process ABCD as depicted in the P-V diagram given below
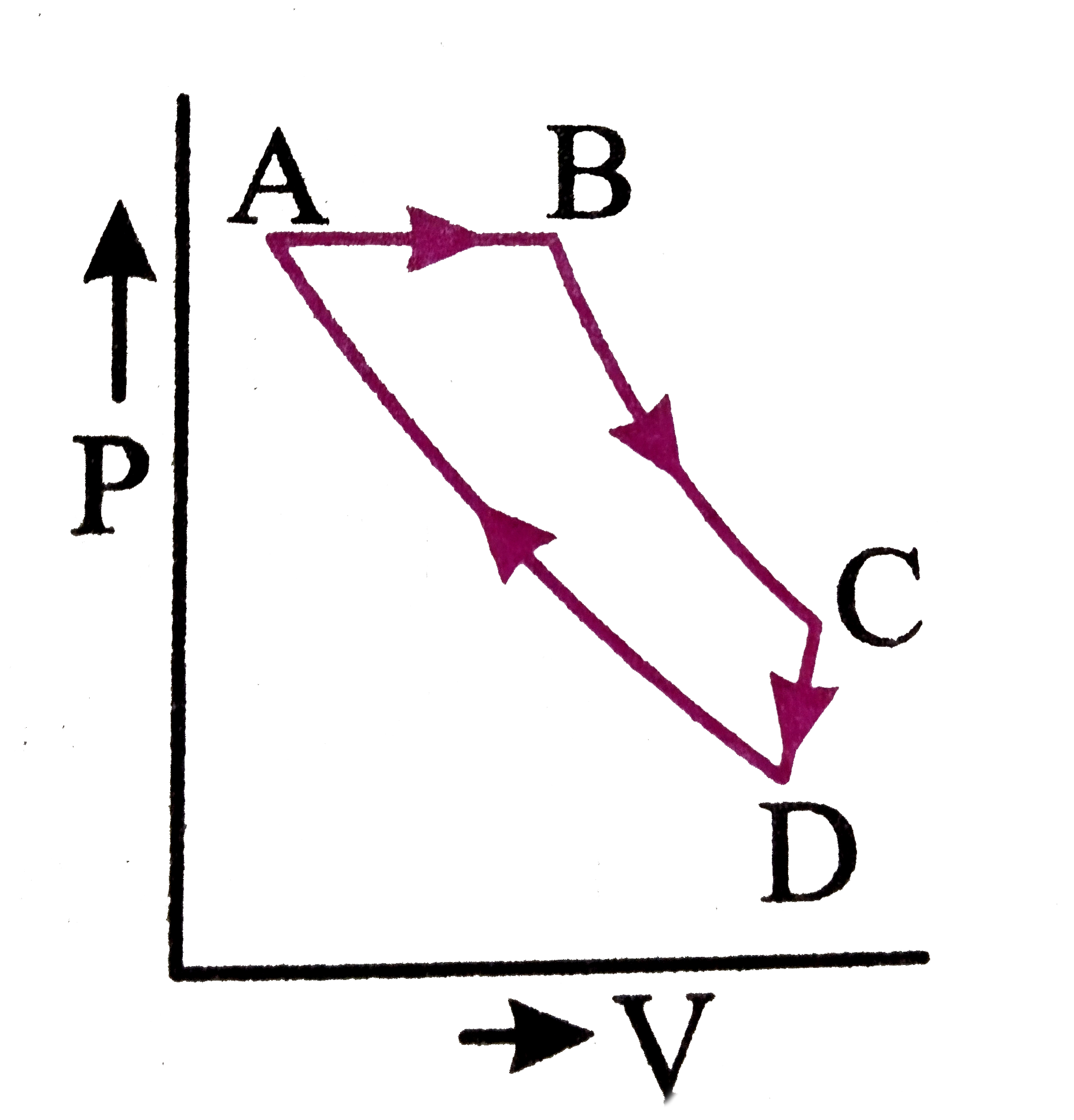
Which of the following curves represents the equivalent cyclic process?
View SolutionA refrigerator, whose coefficient performance `beta` is 5, extracts heat from the collingcompartment at the rate of 250 J per cycle.
(a) How much work per cycle is required to operate the refrigerator?
(b) How much heat per cycle is discharges the room which acts as the high temperature revervoir?
View SolutionA carnot engine operating between temperatures `T_(1)` and `T_(2)` has efficiency. When `T_(2)` is lowered by 62K, its efficience increases to `(1)/(3)`. Then `T_(1)` and `T_(2)` are respectively:
View SolutionFind the efficeincy of the thermodynamic cycle shown in figure for an ideal diatomic gas.
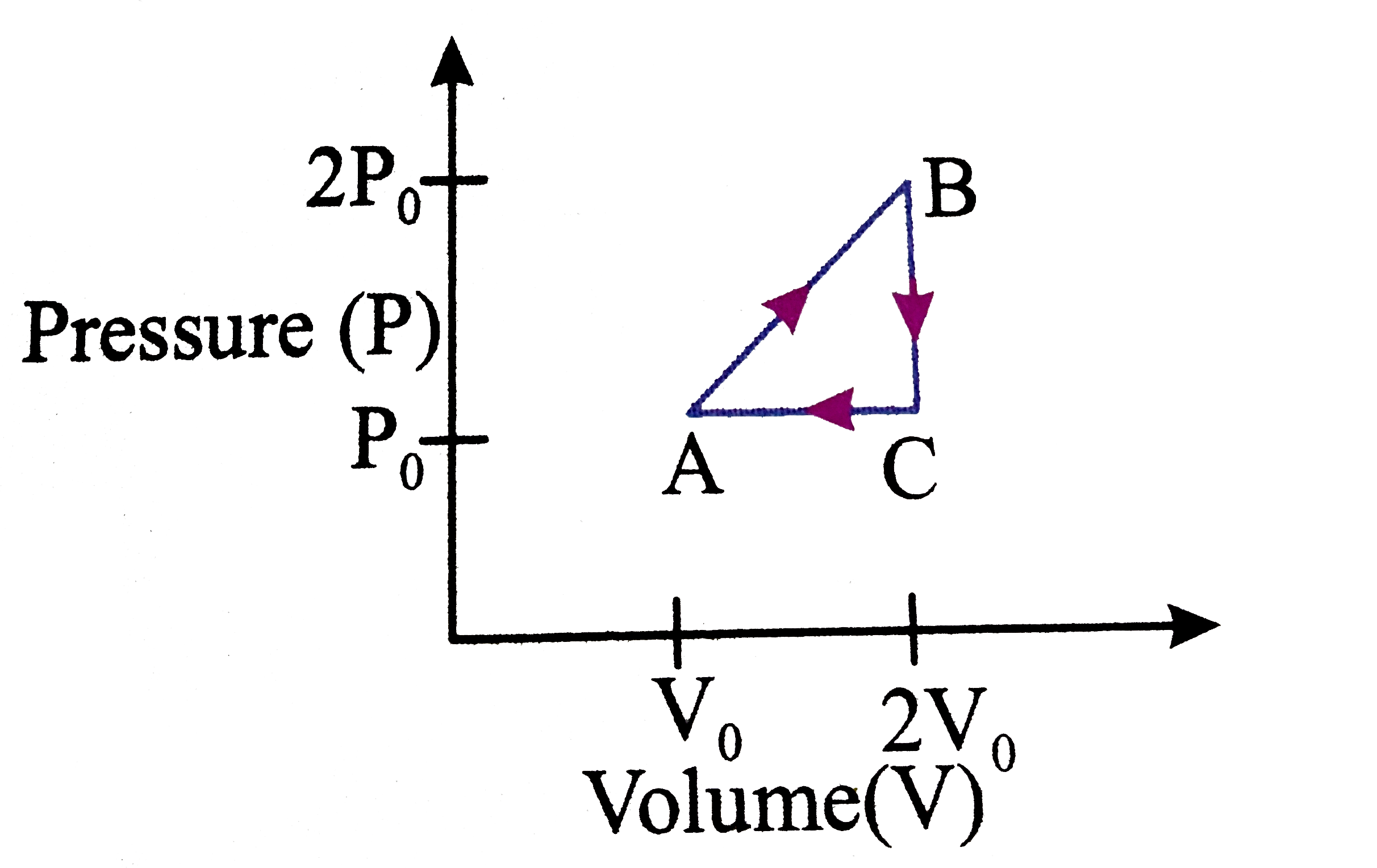
View SolutionA Carnot's engine whose sink is at temperature of 300K has an efficiency of `40%` By how much should the temperature of the source be increased so as to increase the efficiency to 60%?
View SolutionA Carnot engine, having an efficiency of `eta=1//10` as heat engine, is used as a refrigerator. If the work done on the system is 10J, the amount of energy absorbed from the reservoir at lower temperature is
View SolutionHelium gas goes through a cycle ABCDA (consisting of two isochoric and isobaric lines) as shown in figure Efficiency of this cycle is nearly: (Assume the gas to be close to ideal gas)

View SolutionA Carnot engine, whose efficiency is `40%`, takes in heat from a source maintained at a temperature of 500K. It is desired to have an engine of efficiency `60%`. Then, the intake temperature for the same exhaust (sink) temperature must be:
View SolutionA diatomic ideal gas is used in a Carnot engine as the working substance. If during the adiabatic expansion part of the cycle the volume of the gas increase from V to 32V, the efficiency of the engine is
View SolutionAn ideal monoatomic gas undergoes a cyclic process `ABCA` as shown in the figure. The ratio of heat absorbed during `AB` to the work done on the gas during `BC` id
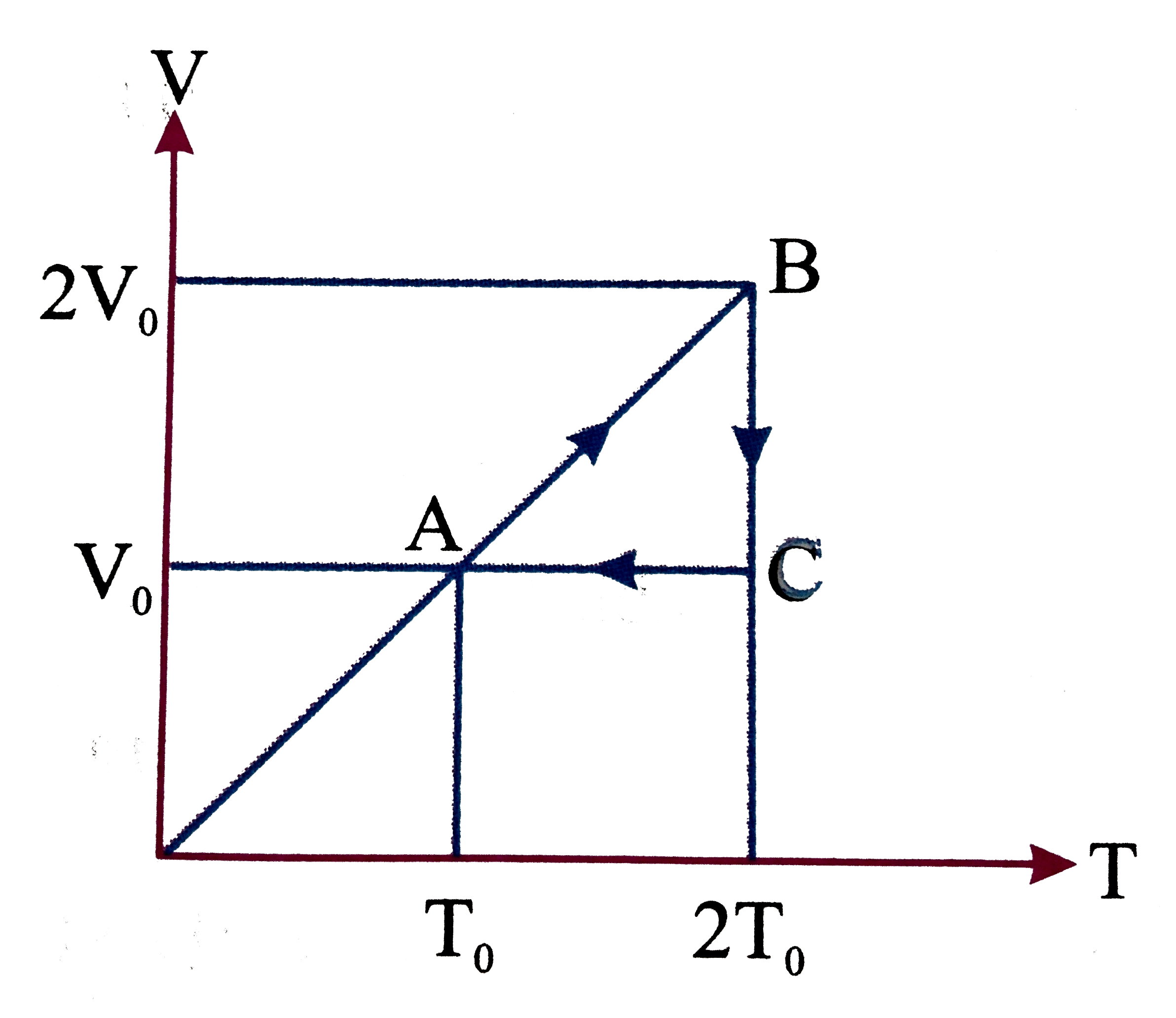
View Solution`3` moles of an ideal mono atomic gas performs a cycle as shown in fig. `If` gas temperature `T_(A)=400 K` `T_(B)=800K,T_(C)=2400K`, and `T_(D)=1200K`. Then total work done by gas is

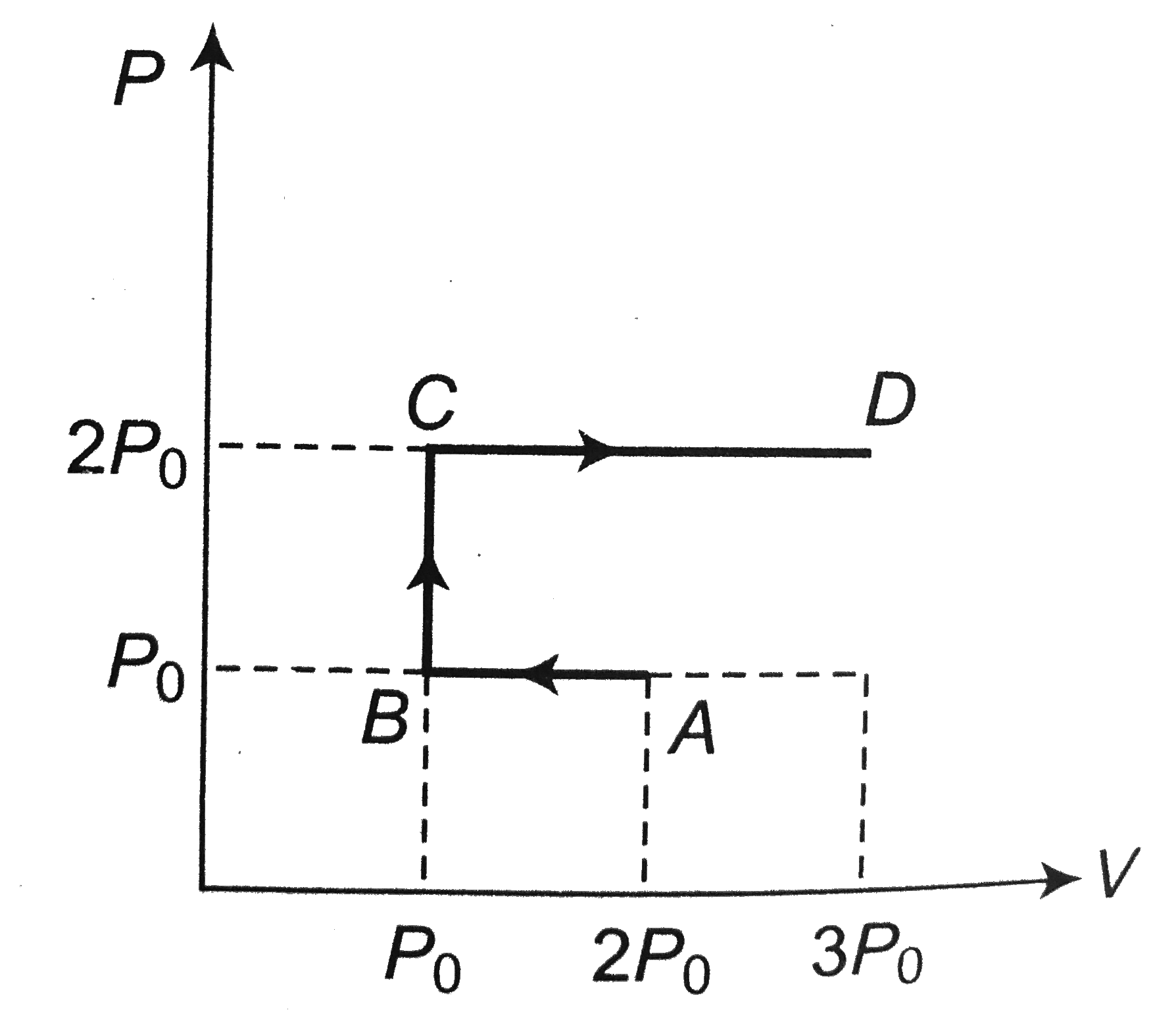
View Solution`P - V` diagram of an ideal gas is as shown in figure. Work done by the gas in process `ABCD` is
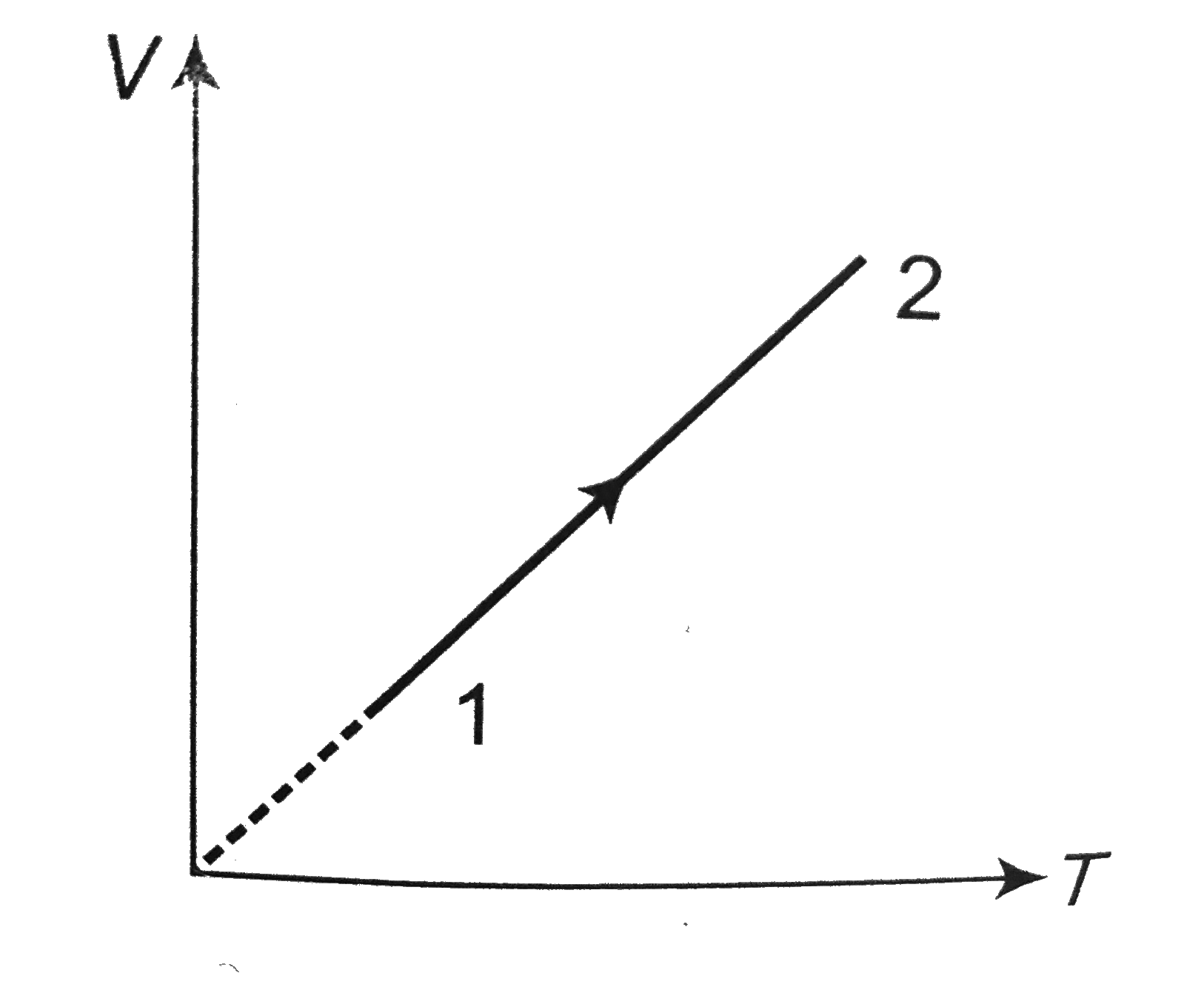
View SolutionVolume versus temperature graph of two moles of helium gas is as shown in figure. The ratio of heat absorbed and the work done by the gas in process `1-2` is
View SolutionPressure versus temperature graph of an ideal gas is shown in figure. Density of the gas at point A is `rho_(0)`. Density at B will be

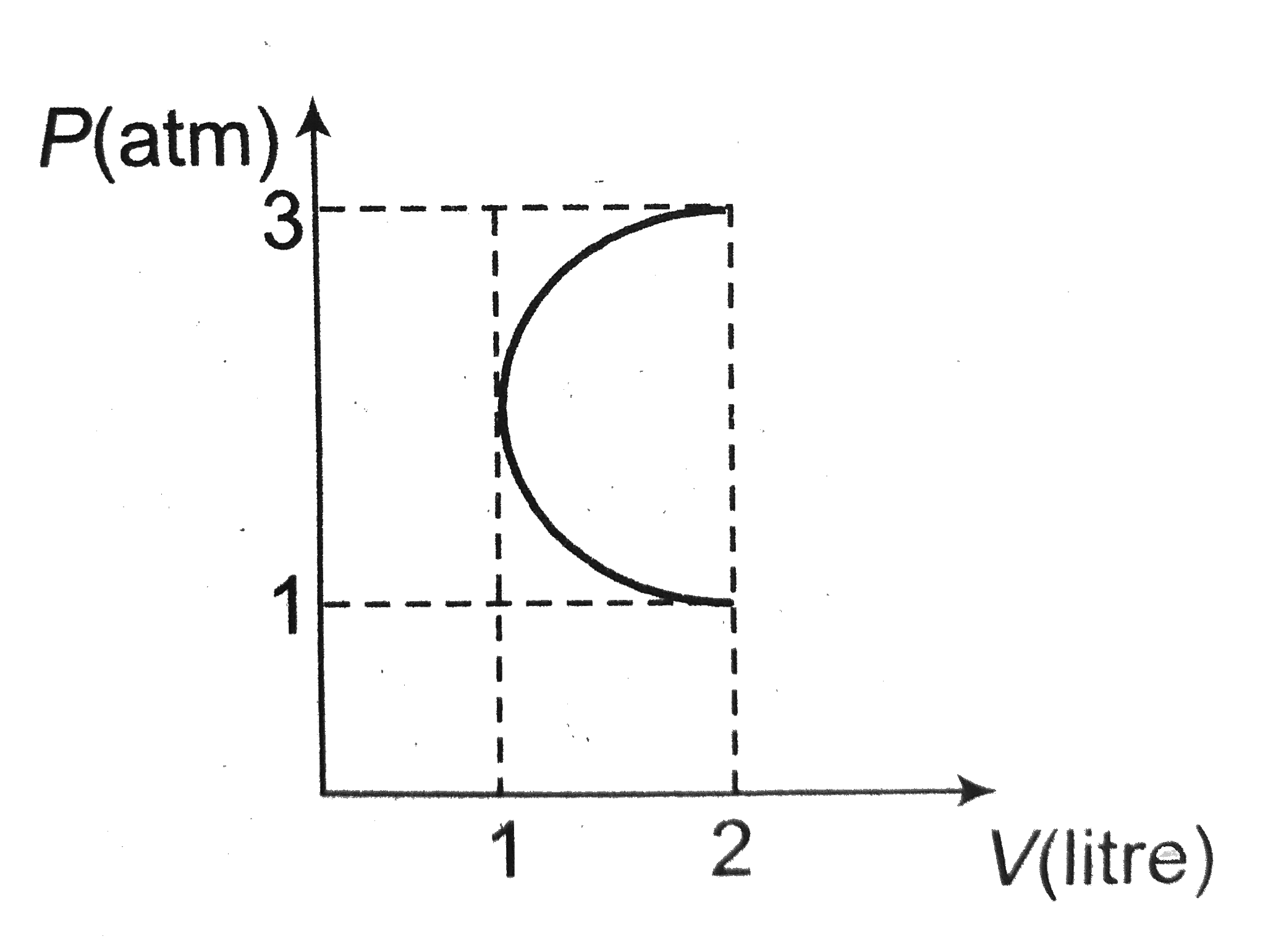
View SolutionIn the `P-V` diagram shown in figure `ABC` is a semicircle. The work done in the process `ABC` is
View SolutionPressure versus temperature graph of an ideal gas as shown in Fig.
Corresponding density `(rho)` versus volume `(V)` graph will be
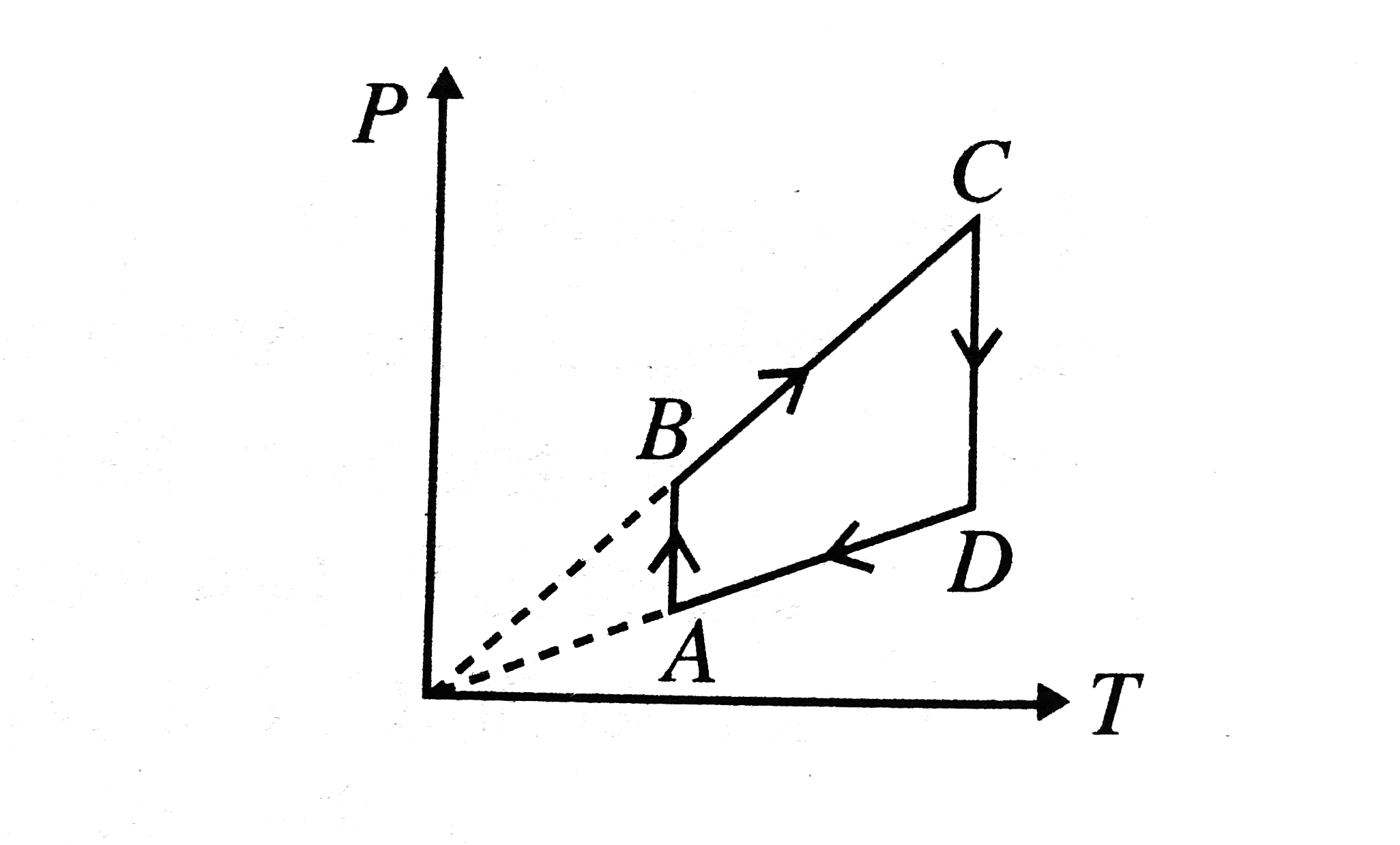
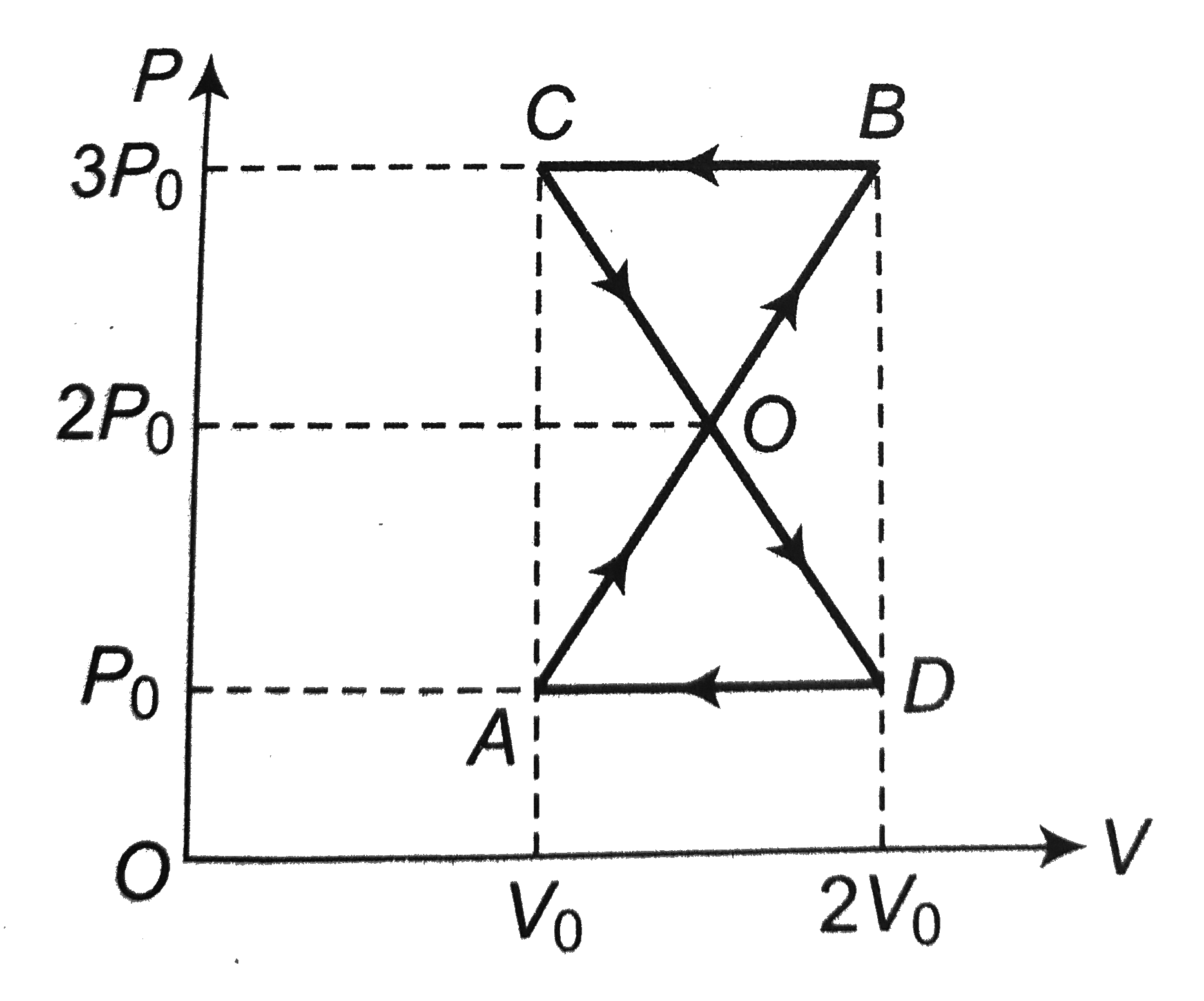
View SolutionA thermodynamic system undergoes cyclic process `ABCDA` as shown in figure. The work done by the system is
View SolutionP-V plots for two gases during adiabatic processes are shown in the figure. Plots 1 and 2 should corresponds respectively to

View SolutionOne mole of a diatomic ideal gas undergoes a cyclic process ABC as shown in figure. The process BC is adiabatic. The temperature at A,B and C are 400K, 800K and 600K respectively. Choose the correct statement:
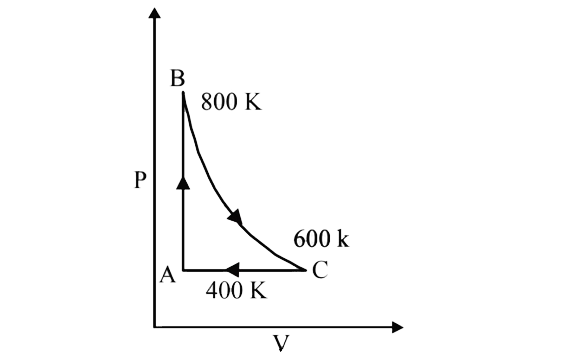
View Solution
SOLVED EXAMPLE questions and complete solutions for chapter KINETIC THEORY OF GASES of NARAYANA PHYSICS (HINGLISH) of Class 11