Complete Solutions to LEVEL-III of chapter MECHANICAL PROPERTIES OF SOLIDS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MECHANICAL PROPERTIES OF SOLIDS |
| NARAYANA | LEVEL-III |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
A wire of length `1m` fixed at one end has a sphere attached to it at the other end. The sphere is projected hroizonatally with a veloicity of `sqrt(9g)`. When it decribes a vertical circle the ratio of elongations of the wire when the sphere is at top and bottom of the circle is
View SolutionA bob of mass `10 kg` is attached to a wire `0.3 m` long. Its breaking stress is `4.8xx10^(7) N//m^(2)`. Then area of cross-section of the wire is `10^(-6) m^(2)`. What is the maximum angular velocity with which it can be rotated in a horizontal circle?
View SolutionA mass `'m' kg` is whirled in a verticle plane by tying it at the end of a flexible wire of length `'L'` and area of cross-section `'A'` such that it just completes the verticle circle. When the mass is a its lowest positon, the strain produced in the wire is (Young's modulus of the wire is `'Y'`)
View SolutionWhen a mass is suspended from the end of wire the top end of which is attached to the roof of the lift, the extension is `'e'` when the lift is stationary . If the lift moves up with constant acceleartion `g//2` the extension of the wire would be
View SolutionA block of mass `1 Kg` is fastened to one each of a wire of cross-sectional area of `2mm^(2)` and is rotated in verticle circle of radius `20cm`. The speed of the block at the bottom of the circle is `3.5ms^(-1)`. The elongation of the wire when the block is at top of the circle
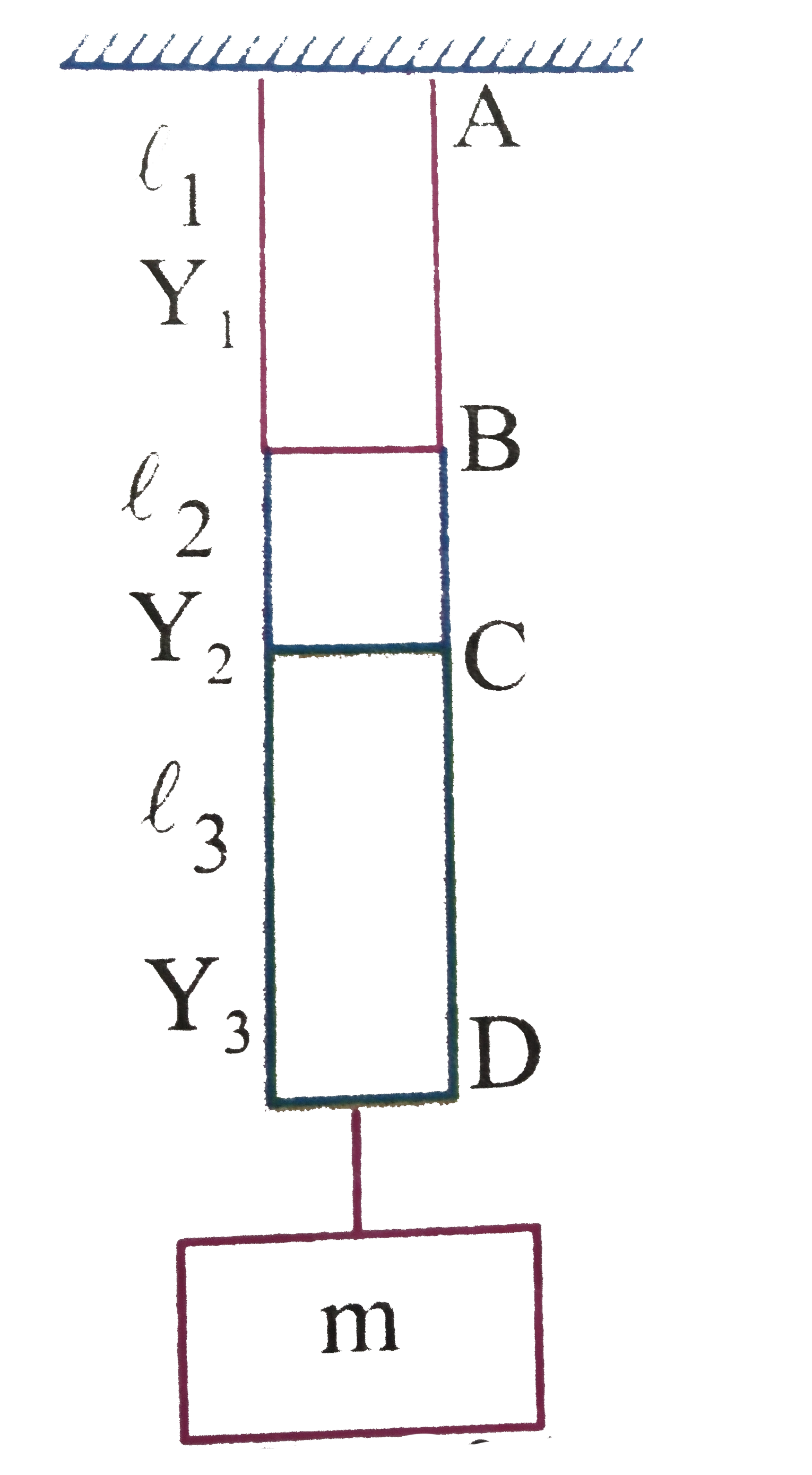
View SolutionAs shown in adjacent figure if a load of mass `(m)` is attached at lower end of wire. Then find the displacement of the points `B,C` and `D` are as shwon in figure.
(i) elongation of first wire `e_(1) = ((mg)l_(1))/(AY_(1))`
(ii) elongation of `2nd` wire
`e_(2) = ((mg)l_(2))/(AY_(2)) + ((mg)l_(1))/(AY_(1))`
(iii) elongation of `3rd` wire
`e_(3) = ((mg) l_(3))/(AY_(3)) + ((mg)l_(2))/(AY_(2)) + ((mg) l_(1))/(AY_(1))`
View SolutionA copper wire of negligilble mas, length `(l)` and cross-sectional area `(A)` is kept on a smooth horizontal table with one end fixed, a ball of mass `'m'` is attached at the other end. The wire and the ball are rotated with angular velocity `'omega'`. If wire elongates by `Delta l` then the Young's modulus of wire and if on incresing the angular velocity from `omega` to `omega^(1)` when the wire breaks-down, then the brekaing stress `(Deltal lt lt l )` are respectivley.
View SolutionA stone of mass `m` tied to one end of a wire of length L. the diameter of the wire is D and it is suspended vertically. The stone is now rotated in a horizontal plane and makes an angle 6 with the vertical. If Young's modulus of the wire is `Y`, Then the increase in the length of the wire is
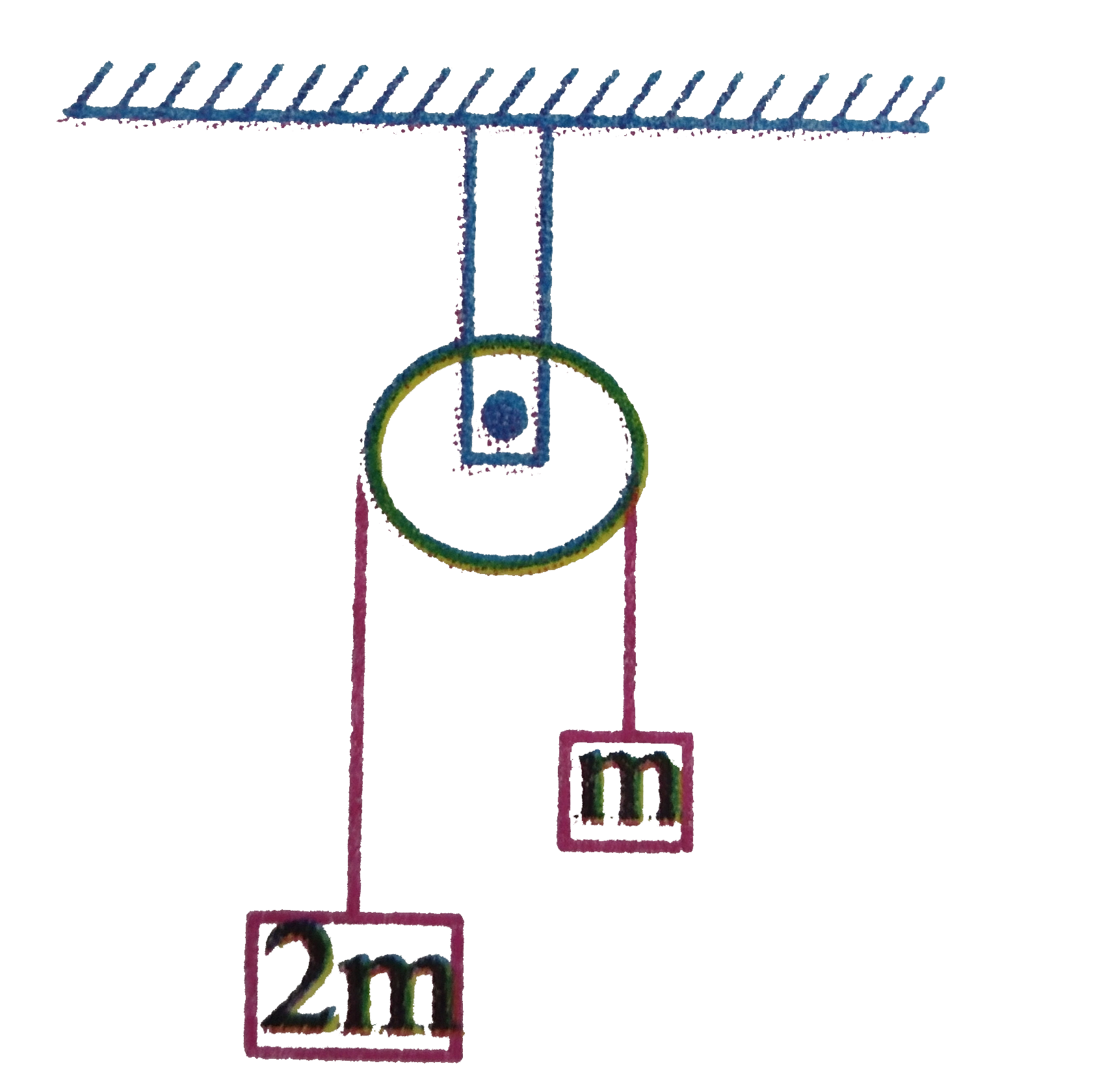
View SolutionTwo blocks of masses `m` and `2m` are connected through a wire fo breakig stress `S` passing over a frictionless pulley. The maximum radius of the wire to be used so that the wire may not break is
View SolutionOne end of a long metallic wire of length (L) is tied to the ceiling. The other end is tied to a massless spring of spring constant . (K.A) mass (m) hangs freely from the free end of the spring. The area of cross- section and the Young's modulus of the wire are (A) and (Y) respectively. If the mass is slightly pulled down and released, it will oscillate with a time period (T) equal to :
View SolutionA wire of cross section `A` is stretched horizontally between two clamps located `2l m` apart. A weight `W kg` is suspended from the mid-point of the wire. If the mid-point sags vertically through a distance `x lt l`, the strain produced is
View SolutionIf in the above question the Young's modulus of the material is Y, the value of extension x is:
View SolutionEach of the three blocks P, Q and R shown in figure has a mass of 3 kg. Easch of the wires A and B has cross sectional area 0.005 cm^2 and Young modulus `2x10^11Nm^-2`. Neglect friction. Find the longitudinal strain developed ineach of the wires. Take `g=10ms^-2`

View SolutionA sphere of radius ` 0.1m` and mass `8 pi` `kg` is attached to the lower end of a steel wire of length `5.0 m` and diameter `10^(-3)m`. The wire is suspended from `5.22 m` high ceiling of a room . When the sphere is made to swing as a simple pendulum, it just grazes the floor at its lowest point. Calculate the velocity of the sphere at the lowest position . Young's modulus of steel is `(1.994xx10^(11) N//m^(2))`.
View SolutionA thin uniform rod of length `l` and masses `m` rotates uniformly with an angularly velocity `omega` in a horizontal plane about a verticle axis passing through one of its ends determine the tension in the rot as a funtion of the distance x from the rotation axis

View SolutionThe wires `A` and `B` shown in Fig. are made of the same material and have radii `r_(A)` and `r_(B)`, respectively. The block between them has a mass `m`. When the force `F` is `mg//3`, one of the wires breaks. Then

View SolutionA wire of radius `r`, Young's modulus `Y` and length `l` is hung from a fizxed point and support a heavty metal cycliner of volume `V` at its own lowest end. The change in length of the wire when cyclinder is immersed in a liquid of density `rho`, is in fact
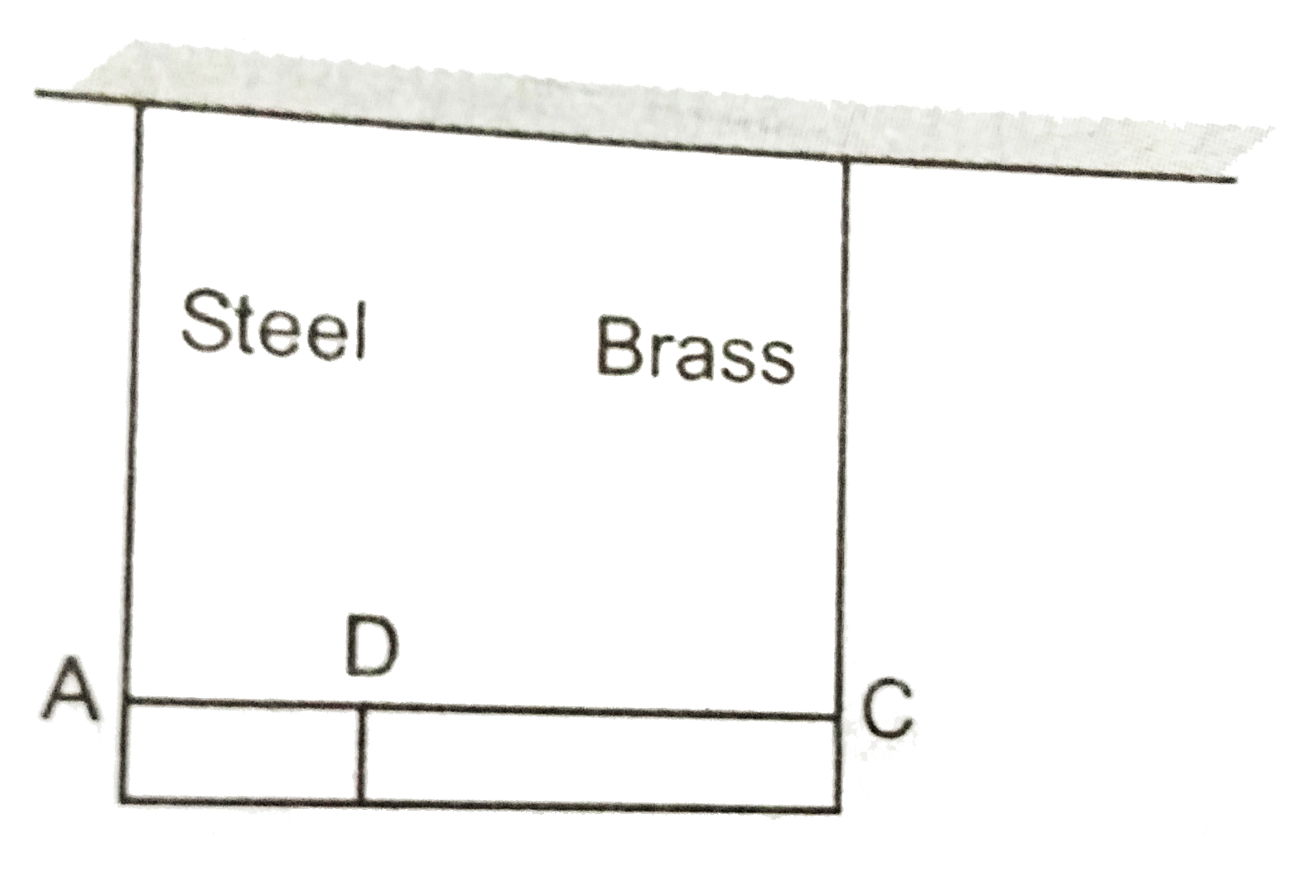
View SolutionA light rod AC of length 2.00 m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section `10^(-3) m^(2)` and the other is of brass of cross-section `2xx10^(-3) m^(2)`. The position of point D from end A along the rod at which a weight may be hung to produce equal stress in both the wires is [Young's modulus of steel is `2xx10^(11) Nm^(2)` and for brass is `1xx10^(11) Nm^(-2)`]
View SolutionA steel rod of cross-sectional area `16 cm^(2)` and two brass rods each of cross-sectional area `10 cm^(2)` together support a load of `5000 kg ` as shown in the figure. ( Given, `Y_(steel) = 2xx10^(6) kg cm^(-2) and Y_(brass) = 10 ^(6) kg cm^(-2))`. Choose the correct option(s).

View SolutionIf the ratio of lenghts, radi and Young's moduli of steel and brass wires are `a,b` and `c` respectively their respective loads are in the ratio `3:2` then the corresponding ratio of increases in their lenghts would be
View SolutionA uniform rod of length `L`, has a mass per unit length `lambda` and area of cross section `A`. The elongation in the rod is `l` due to its own weight, if it suspended form the celing of a room. The Young's modulus of the rod is
View SolutionThe torque required to produce a unit twist in a solide bar of length `L` and radius `r` is
View SolutionA uniform pressure P is exerted by an external agent on all sides of a solid cube at temperature `t^(@)C`. By what amount should the temperature of the cube be raised in order to bring its volume back to its original volume before the pressure was applied if the bulk modulus is B and co-efficient of volumetric expansion is `gamma`?
View SolutionThe density of water at the surface of ocean is `rho` . If the bulk modulus of water is `B`, then the density of ocean water at depth, when the pressure at a depth is `alphap_(0)` and `p_(0)` is the atmospheric pressure is
View SolutionWhat is the density of lead under a pressure of `2.0xx10^(8) N//m^(2) ` , if the bulk modulus of lead is ` 8.0xx10^(9) N//m^(2)` and initially the density of lead is `11.4 g//cm^(3)`?
View SolutionHow does the density of sea water change with depth?
View SolutionA rubber cord has a cross -sectional area `1 mm^(2)`and total unstretched length`10.0cm`. It is streched to `12.0 cm` and then released to project a missile of mass 5.0 g.Taking young's modulus Y for rubber as `5.0xx10^(8) N//m^(2)`.Calculate the velocity of projection .
View SolutionOn loading a metal wire of cross section `10^(-6) m^(2)` and length `2m` by a mass of `210kg`, it extends by `16mm` and suddenly broke form the point of support . If denstiy of that metal is `8000K gm^(-3)` and its specific heat is `420J Kg^(1) K^(-1)` the ride in temperature of wire is
View SolutionA long wire hangs vertically with its upper end clamped. A torque of `8 Nm` applied to the free end that twists it through`45^@`. The potential energy of the twisted wire is
View Solution
LEVEL-III questions and complete solutions for chapter MECHANICAL PROPERTIES OF SOLIDS of NARAYANA PHYSICS (HINGLISH) of Class 11