Complete Solutions to Passage Type Questions of chapter MOTION IN A STRAIGHT LINE of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN A STRAIGHT LINE |
| NARAYANA | Passage Type Questions |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
A monkey climbs up a slippery pole for ` 3 seconds` and subsequently slips for `3 seconda`. Its velocity at time (t) is given by ` v (t) =2 t (3-t) , 0 lt tgt 3 s and v (t) =- (t-30 (6-t) for 3 lt tlt 6 s in m//s`. It repeats thei cycle till it reaches the height of ` 20 s.`
(a) AT wht time is its v elocity maximum ? (b) At what time is its average velocity maximum ? (c ) At what time is its accelration maximum in magnitude ? (d) How many cycles (counting fractions ) are required to reach the top ?
View SolutionA monkey climbs up a slippery pole for ` 3 seconds` and subsequently slips for `3 seconda`. Its velocity at time (t) is given by ` v (t) =2 t (3-t) , 0 lt tgt 3 s and v (t) =- (t-30 (6-t) for 3 lt tlt 6 s in m//s`. It repeats thei cycle till it reaches the height of ` 20 s.`
(a) AT wht time is its v elocity maximum ? (b) At what time is its average velocity maximum ? (c ) At what time is its accelration maximum in magnitude ? (d) How many cycles (counting fractions ) are required to reach the top ?
View SolutionA monkey climbs up a slippery pole for ` 3 seconds` and subsequently slips for `3 seconda`. Its velocity at time (t) is given by ` v (t) =2 t (3-t) , 0 lt tgt 3 s and v (t) =- (t-30 (6-t) for 3 lt tlt 6 s in m//s`. It repeats thei cycle till it reaches the height of ` 20 s.`
(a) AT wht time is its v elocity maximum ? (b) At what time is its average velocity maximum ? (c ) At what time is its accelration maximum in magnitude ? (d) How many cycles (counting fractions ) are required to reach the top ?
View SolutionA monkey climbs up a slippery pole for ` 3 seconds` and subsequently slips for `3 seconda`. Its velocity at time (t) is given by ` v (t) =2 t (3-t) , 0 lt tgt 3 s and v (t) =- (t-30 (6-t) for 3 lt tlt 6 s in m//s`. It repeats thei cycle till it reaches the height of ` 20 s.`
(a) AT wht time is its v elocity maximum ? (b) At what time is its average velocity maximum ? (c ) At what time is its accelration maximum in magnitude ? (d) How many cycles (counting fractions ) are required to reach the top ?
View SolutionA particle executes the motion described by `x (t)=x_(0) (1-e^(-gamma t)) , t gt =0, x_0 gt 0`.
(a) Where does the particle start and with what velocity ?
(b) Find maximum and minimum values of ` x (t) , a (t)`. Show that ` x (t) and a (t)` increase with time and ` v(t)` decreases with time.
View SolutionA particle executes the motion described by `x (t)=x_(0) (1-e^(-gamma t)) , t gt =0, x_0 gt 0`.
(a) Where does the particle start and with what velocity ?
(b) Find maximum and minimum values of ` x (t) , a (t)`. Show that ` x (t) and a (t)` increase with time and ` v(t)` decreases with time.
View SolutionA particle executes the motion described by `x (t)=x_(0) (1-e^(-gamma t)) , t gt =0, x_0 gt 0`.
(a) Where does the particle start and with what velocity ?
(b) Find maximum and minimum values of ` x (t) , a (t)`. Show that ` x (t) and a (t)` increase with time and ` v(t)` decreases with time.
View SolutionA particle exceutes the motion describes by
`x(t)=x_(0)(1-e^(-gammat)),tge0,x_(0)0`.
The maximum and minimum values of `v(t)` are
View SolutionA particle executes the motion described by `x (t)=x_(0) (1-e^(-gamma t)) , t gt =0, x_0 gt 0`.
(a) Where does the particle start and with what velocity ?
(b) Find maximum and minimum values of ` x (t) , a (t)`. Show that ` x (t) and a (t)` increase with time and ` v(t)` decreases with time.
View SolutionA train starts from rest with constant acceleration `a=1 m//s^(2)` A passenger at a distance S from the train runs at this maximum velocity of `10 m//s` to catch the train at the same moment at which the train starts.
If `S=25.5` m and passenger keeps running, find the time in which he will catch the train:
View SolutionA train starts from rest with constant acceleration `a=1 m//s^(2)` A passenger at a distance S from the train runs at this maximum velocity of `10 m//s` to catch the train at the same moment at which the train starts.
Find the critical distance `S_(c)` for which passenger will take the ten seconds time to catch the train
View SolutionA train starts from rest with constant acceleration `a=1 m//s^(2)` A passenger at a distance S from the train runs at this maximum velocity of `10 m//s` to catch the train at the same moment at which the train starts.
Find the speed of the train when the passenger catches it for the critical distance:
View SolutionA body is moving with uniform velocity of `8 ms^-1`. When the body just crossed another body, the second one starts and moves with uniform acceleration of `4 ms^-2`. The time after which two bodies meet will be :
View SolutionA body is moving with uniform velocity of `8 m s^(-1)`. When the body just crosses another body, the second one starts and moves with uniform acceleration of `4 m s^(-2)`.
The distance covered by the second body when they meet is .
View SolutionStudy the following graph:
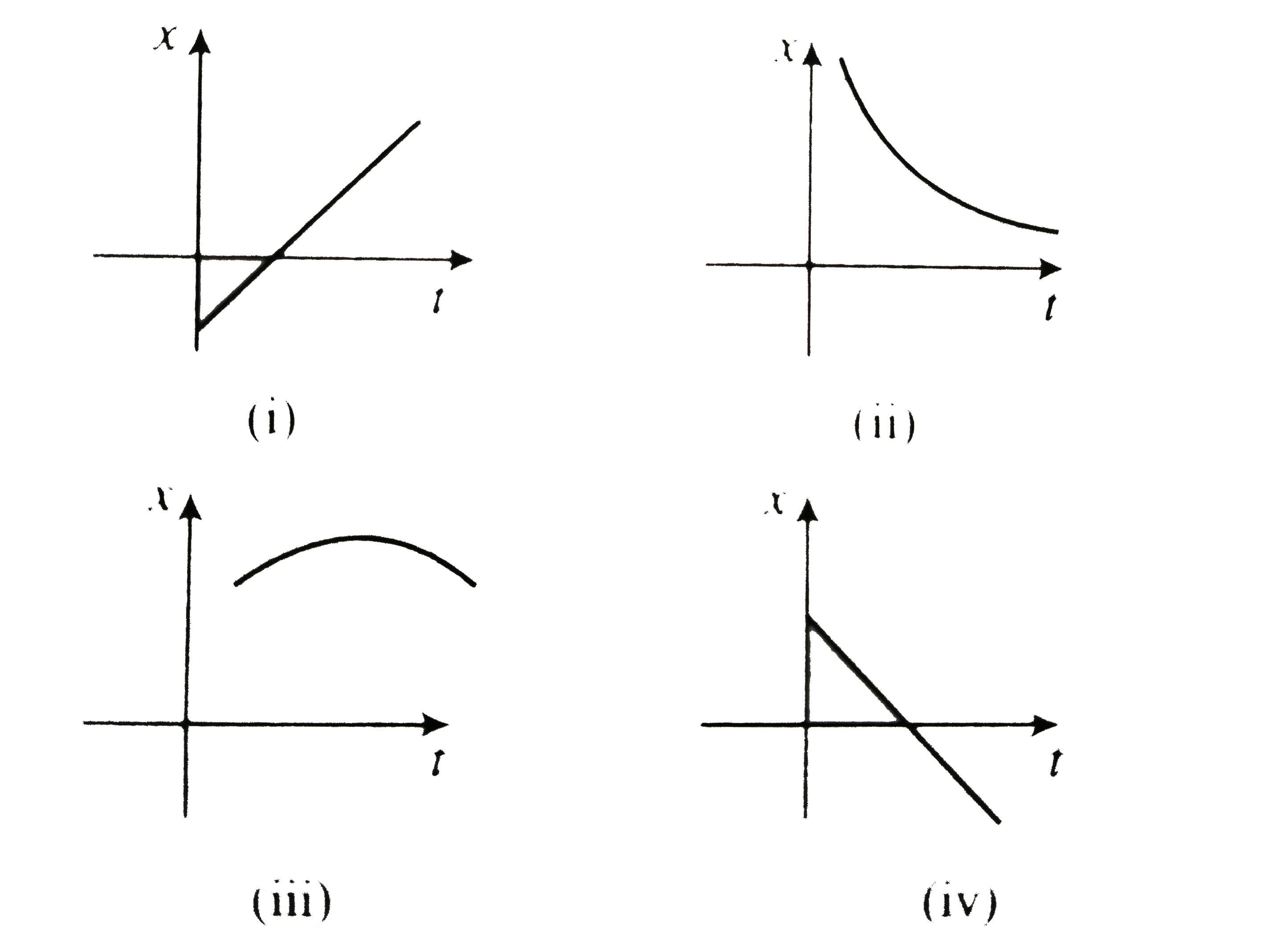
The particle is moving with constant speed .
View SolutionStudy the following graph:
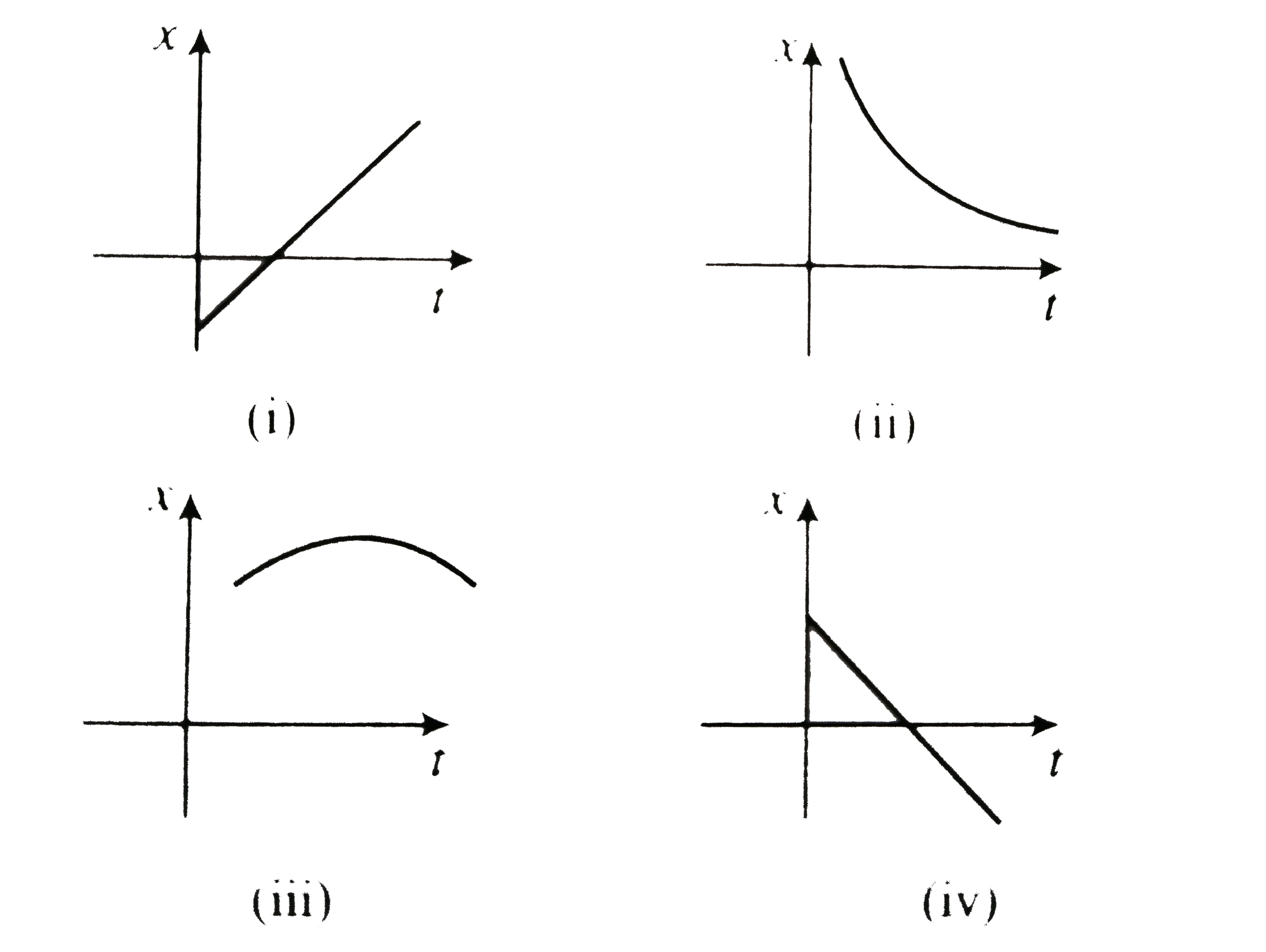
The particle has negative acceletation.
View Solution
Passage Type Questions questions and complete solutions for chapter MOTION IN A STRAIGHT LINE of NARAYANA PHYSICS (HINGLISH) of Class 11