Complete Solutions to Examples of chapter MOTION IN A STRAIGHT LINE of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN A STRAIGHT LINE |
| NARAYANA | Examples |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
An athelete completes one round of a circular track of radius `R` in 40 seconds. What will be the displacement at the end of ` 2 min. 20 second ?
View SolutionIf the position of a particle along Y axis is represented as a funtion of time t by the equation `y(t)=t^(3)` then find displacement of the particle during the period t to `t+Deltat`
View SolutionShows a particle starting from point `A`,travelling up to `B` with a speed `s`, then up to point `C` with a speed `2s`, and finally up to `A` with a speed of `3s`, Determine its average speed.
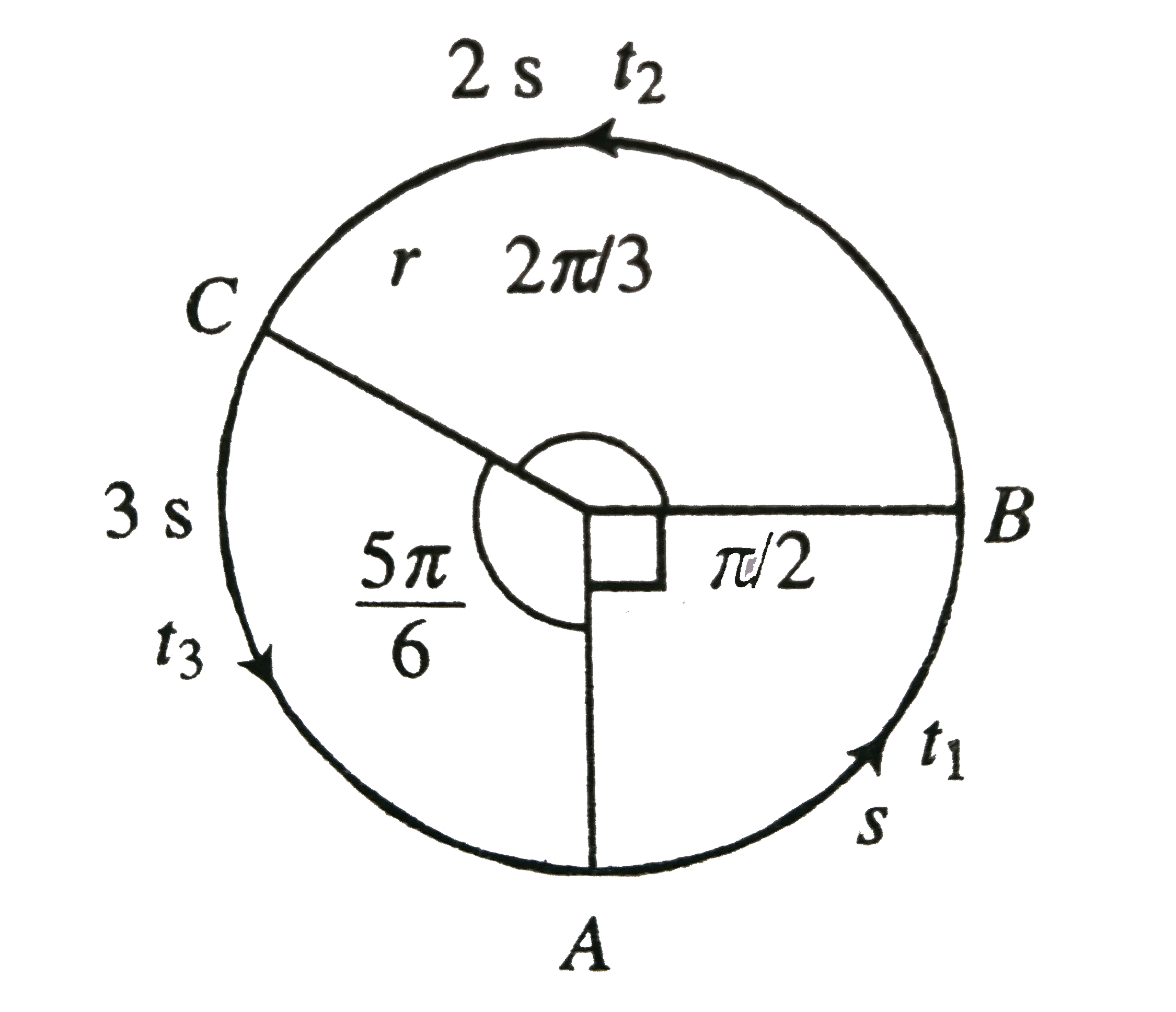 .
.
View SolutionFor a man who walks 72 m at a uniform speed of `2 m//s`, then runs at a uniform speed of `4 m//s` for 5 minute and then again walks at a speed of `1 m//s` for 3 minutes. His average speed is
View SolutionA particle is at `x=_5 m` at `t=0,x=-7 m` at `t=6s` and `x=+2 m` at `t =10s`, find the average velocity of the particle during the interval (a) `t=0` to `t=6s`, (b) `t=6s` to `t=10s`, (c) `t=0` to `t=10s`
View SolutionA particle traversed on third of the distance with a velocity `v_(0)`, the remaining part of the distance was covered with velocity `v_(1)` for half the time and with a velocity `v_(2)` for the remaining half of time. Assuming motion to be rectilinear, find the the mean velocity of the particle averaged over the whole time of motion.
View SolutionA body covers 100 cm in first 2 seconds and 128 cm in the next four seconds moving with constant acceleration. Find the velocity of the body at the end of 8 sec?
View SolutionA car starts from rest and moves with uniform acceleration `a`, At the same instant from the same point a bike crosses with a uniform velocity `u`. When and there will they meet ? What is the velocity of car with respect to the bike at the time of meeting?
View Solution(a) What does `|(dv)/(dt)|` and `(d|v|)/(dt)` represent? (b) Can these be equal?
View SolutionIn a car race, car `A` takes `t_0` time less to finish than car `B` and passes the finishing point with a velocity `v_0` more than car `B`. The cars start from rest and travel with constant accelerations `a_1 and a_2`. Then the ratio `(v_0)/(t_0)` is equal to.
View SolutionA drunkard waking in a barrow lane takes ` 5` steps forward and `3` steps backward, followed again `5` steps forward and `3` steps backward, and so on. Each step is ` 1 m`long and requires 1 s. Determine how long the drunkard takes to fall in a pit ` 13 m` away from start.
View SolutionAn `alpha` particle travels inside a strainght hollow tube 2m long of a particle acceleration under uniform acceleration. How long is the particle in the tube if it enters at a speed of `1000 m//s` and leaves at `9000 m//s`. What is its acceleration during this interval?
View SolutionA car starts from rest and moves along the x-axis with constant acceleration `5 ms^(-2)` for `8` seconds. If it then continues with constant velocity, what distance will the car cover in `12` seconds since it started from the rest ?
View SolutionA car is moving wth a velocity of `40 m//s` the driver sees a stationary truck a head at a distance of 200 m. After some reaction time `Delta t` the breaks are applied producing a (reaction) retardation of `8 m//s^(2)`. What is the maximum reaction time to avoid collision ?
View SolutionTwo trans one t ravelling at 54 kmph and the other at 72 kmph are headed towards one another along a straingt track. When they are `1//2` km apart, both drivers simultaneously seee the other train and apply their brakes. If each train is decelerated at the rate of `1 m//s^(2)`, will there be a collision ?
View Solution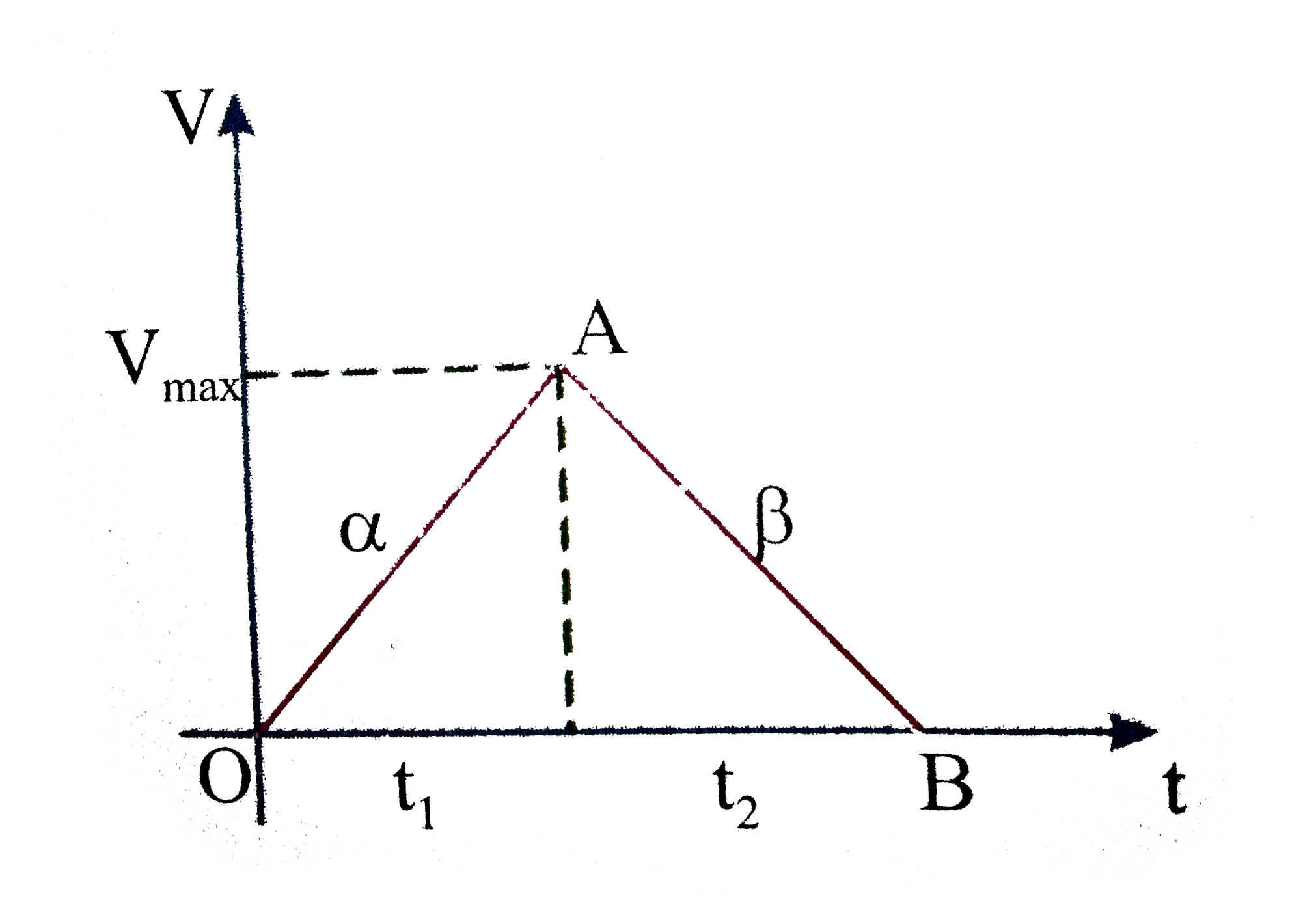
A bus accelerated from rest at a constant rate `alpha` for some time, after which it decelerates at a constant rate `beta` to come to rest. If the total time elapsed is t seconds. Then evaluate following parameters from the given graph
(a) the maximum velocity achieved.
(b) the total distance travelled graphically and
(c) Average velocity.
View SolutionA body starts from rest and travels a distance `S` with uniform acceleration, then moves uniformly a distance `2S` uniformly , and finally comes to rest after moving further `5S` under uniform retardation. The ratio of the average velocity to maximum velocity is.
View SolutionThe acceleration-displacement graph of a particle moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is `s=12 m`.
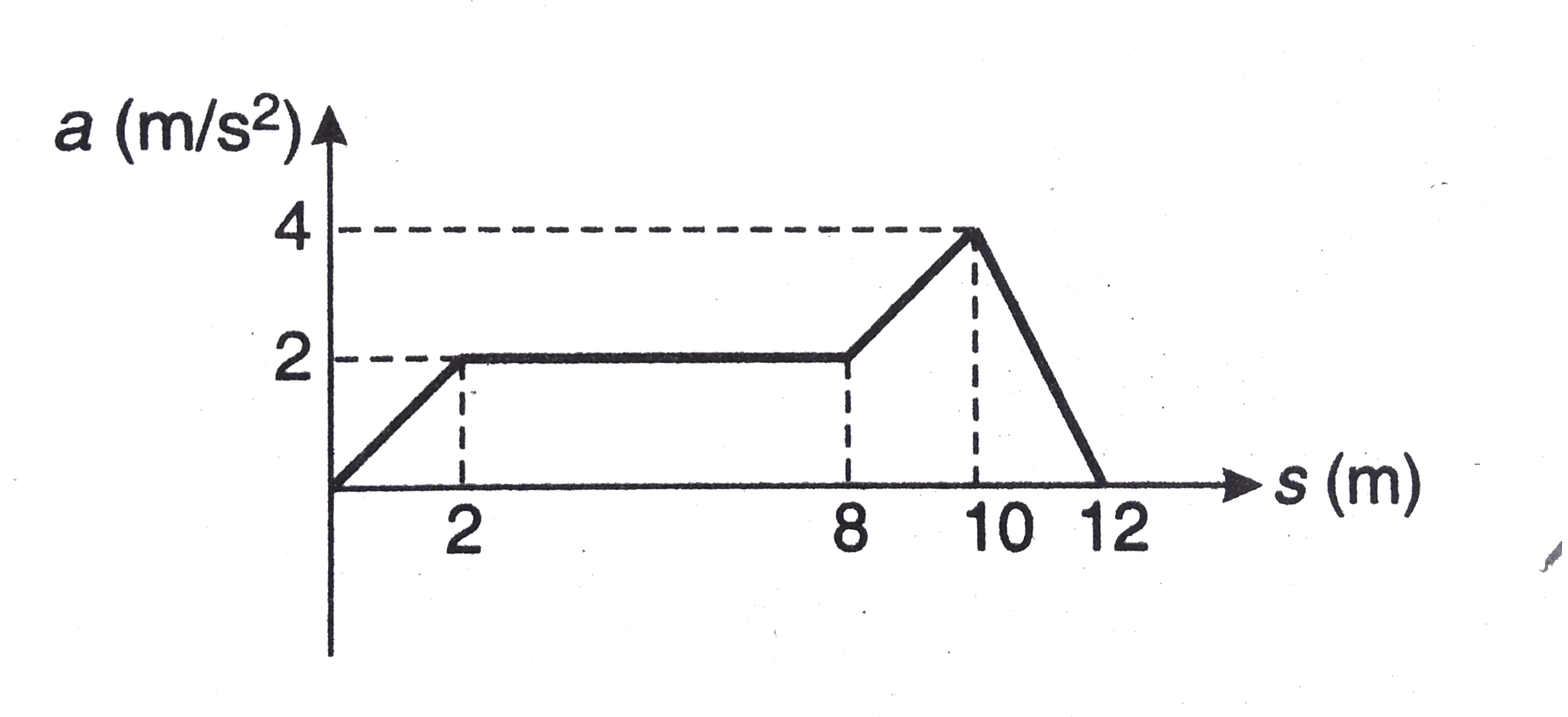
View Solution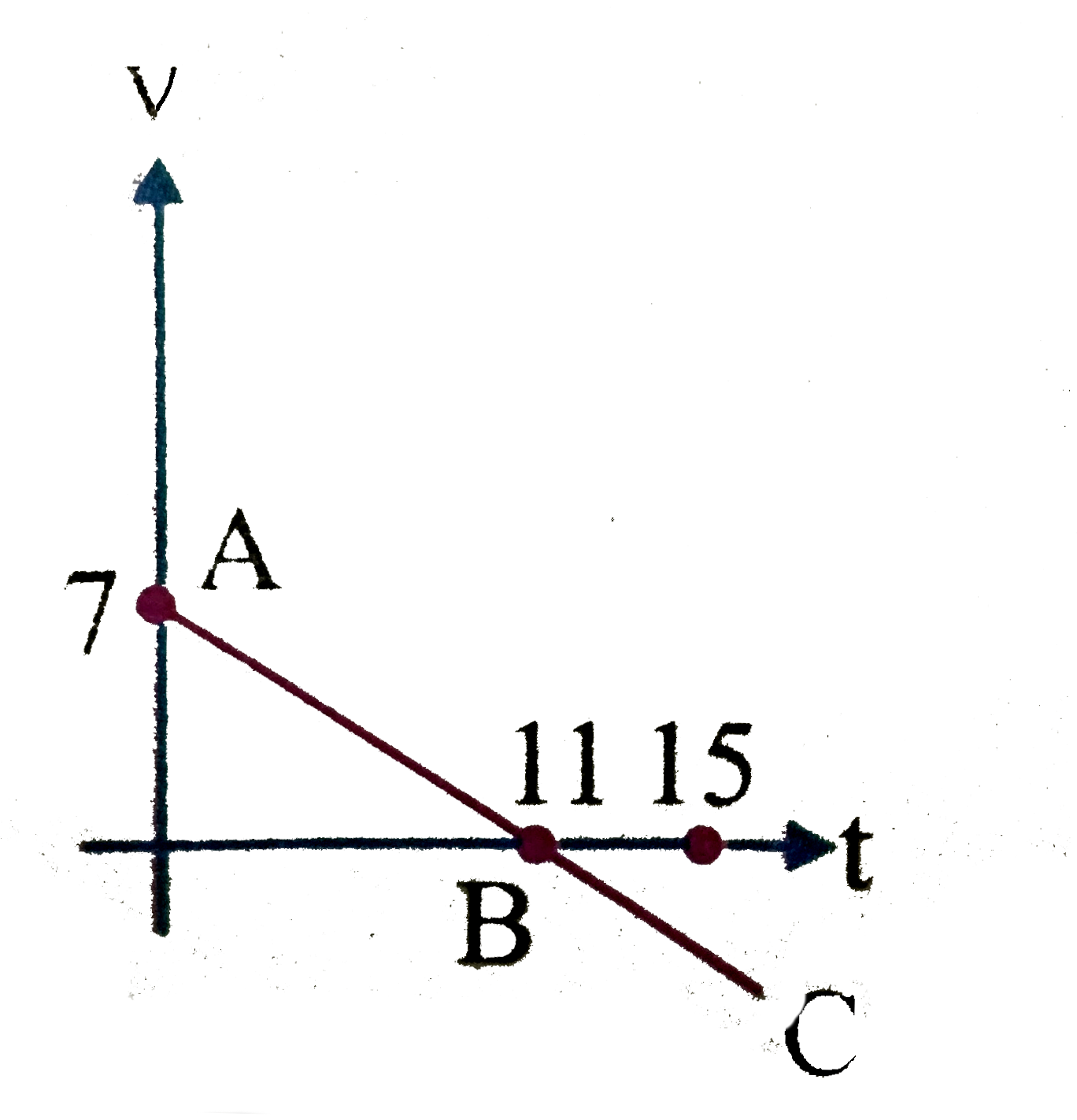
Velocity-time graph for the motion of a certain body is shown in fig. Explain the nature of this motion. Find the initial velocity and acceleration and write the equation for the variation of displacement with time. What happens to the moving body at point B? how will the body more after this moment?
View Solution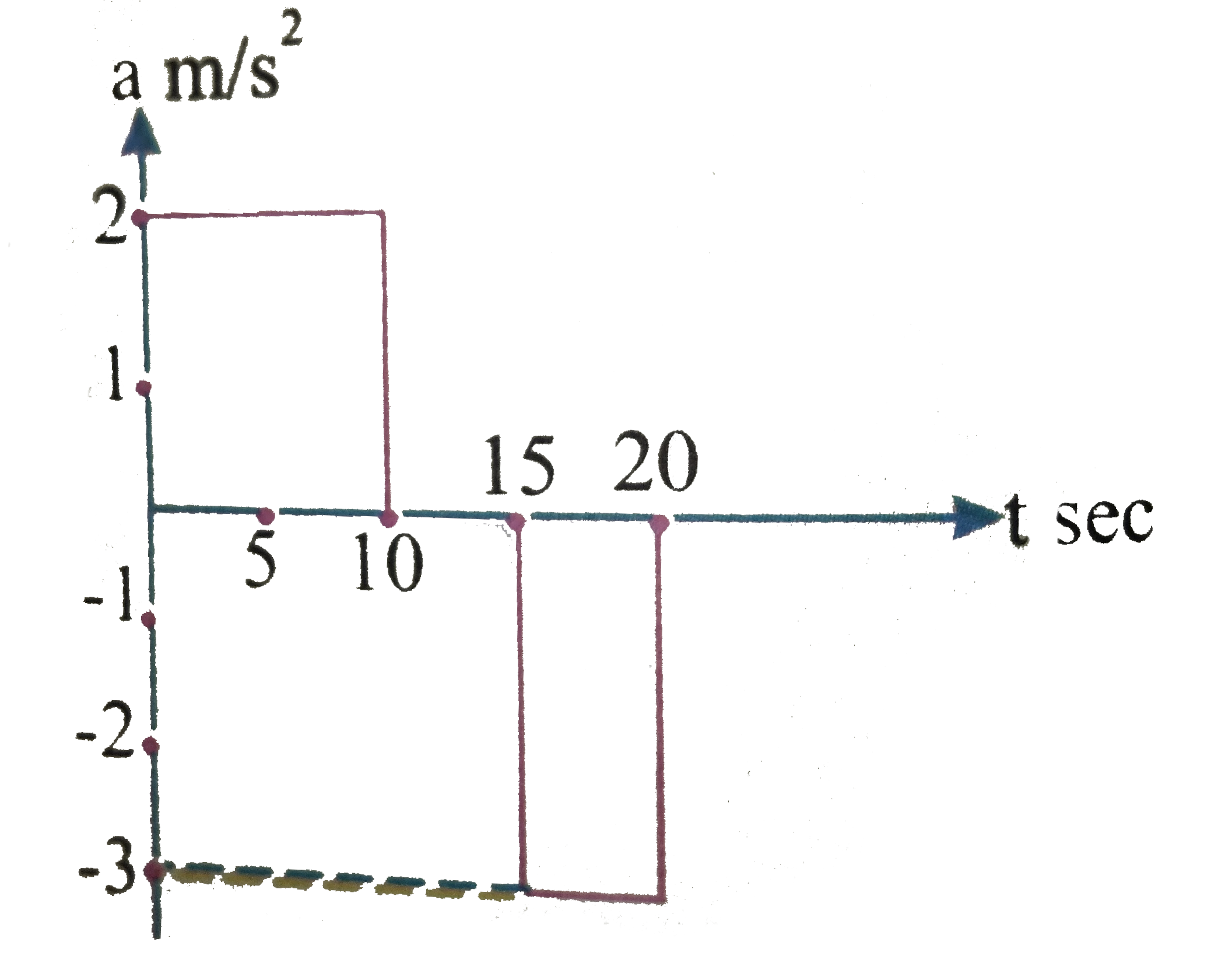
A particle starts from rest and accelerated as shown in the graph. Determine
(a). The particle's speed at `t=10s` and at `t=20 s`
(b). The distance travelled in the first `20s`.
View Solution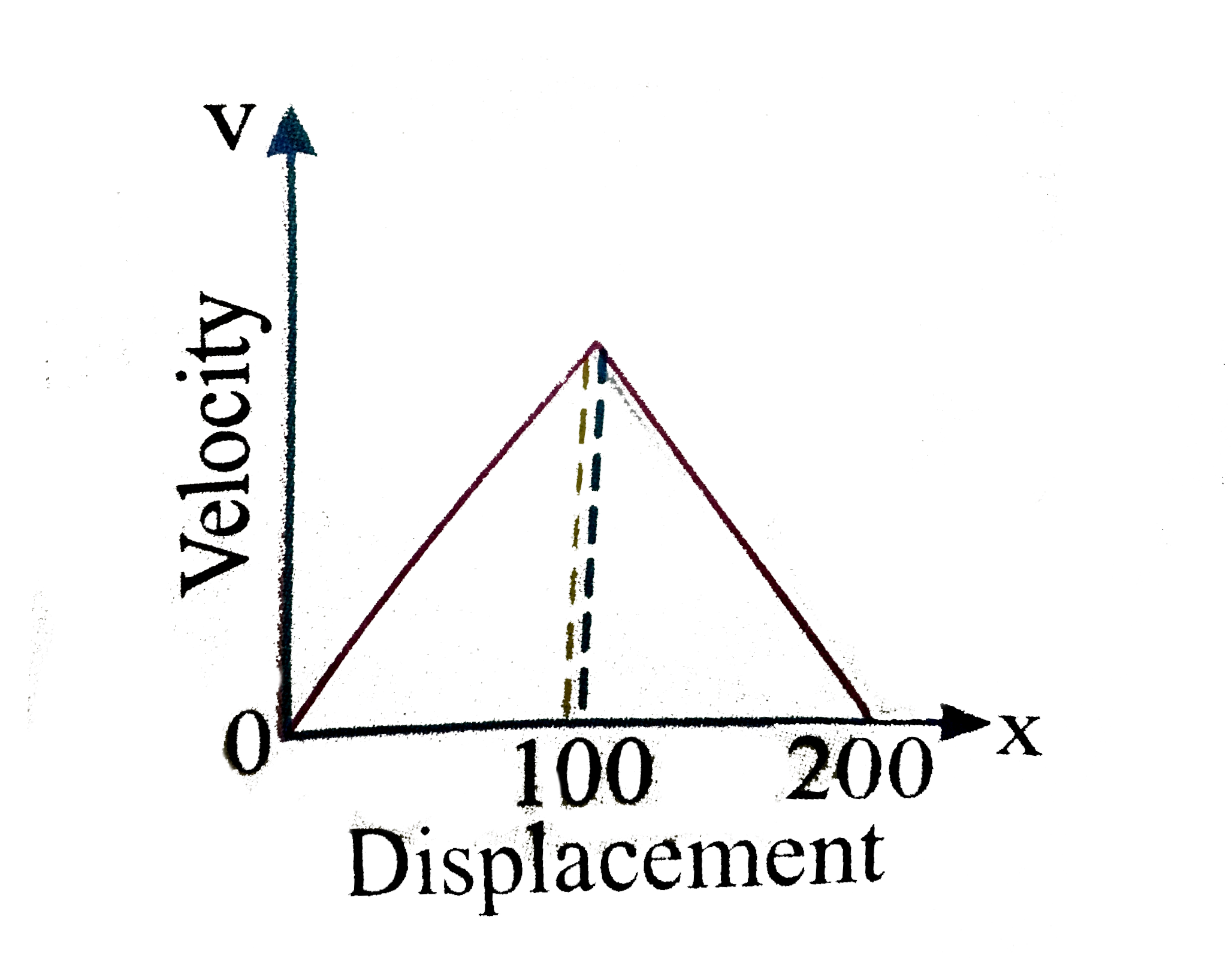
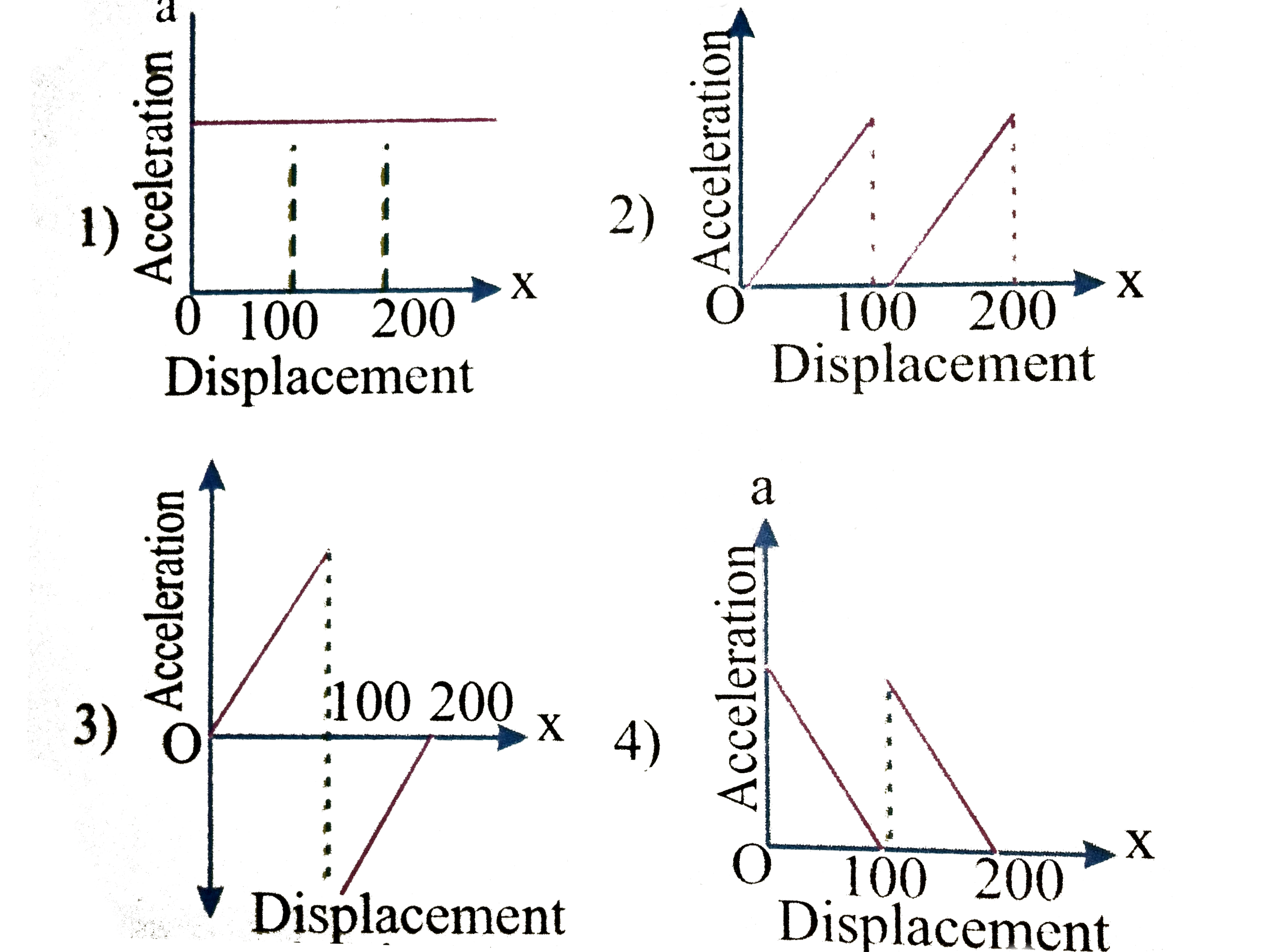
Velocity (v) versus desplacement (x) plot of a body moving along a straight line is as shown in the graph. The corresponding plot of acceleration (a) as a function of displacement (x) is
View SolutionA particle located at `x = 0` at time `t = 0`, starts moving along with the positive ` x-direction` with a velocity 'v' that varies as ` v = a sqrt(x)`. The displacement of the particle varies with time as
View SolutionThe acceleration (a) of a particle moving in a straight line varies with its displacement (S) as `a=2S`. The velocity of the particle is zero and zero displacement. Find the corresponding velocity-displacement equation.
View SolutionAn object , moving with a speed of ` 6.25 m//s `, is decelerated at a rate given by :
`(dv)/(dt) = - 2.5 sqrt (v)` where `v` is the instantaneous speed . The time taken by the object , to come to rest , would be :
View SolutionThe velocity of a particle moving in the positive direction of the X-axis varies as `V=Ksqrt(S)` where K is a positive constant. Draw `V-t` graph.
View SolutionDrops of water fall at regular intervals from the roof of a building of height `h=16m`. The first drop striking the ground at the same moment as the fifth drop is ready to leave from the roof. Find the distance betweent he successive drops.
View SolutionA body falls freely from a height of 125 m `(g=10 m//s^(2))`. After 2 sec gravity ceases to act find time taken by it to reach the ground?
View SolutionA parachutist drops freely from an aeroplane for 10 seconds before the parachute opens out. Then he descends with a net retardation of `2 m//s^(2)`. His velocity when he reaches the ground is `8 m//s` find the height at which he gets out of the aeroplane?
View SolutionIf body travels half of its path in the last second of its fall from rest, find the time and height of its fall.
View SolutionA body is projected vertically up with a valocity u. its velocity at ghalf of its maximum height and at `3//4th` of its maximum height are.
View Solution
A stone is allowed to fall from the top of a tower 300 m height and at the same time another stone is projected vertically up from the ground with a velocity `100 m//s`. Find when and where the two stones meet?
View SolutionA stone is dropped from certain height above the ground. After 5 s a ball passes trhough a pane of glass held horizontally and instantaneously loses `20%` of its velocity. If the ball takes 2 more seconds to reach the ground the height of the glass above the ground is
View SolutionA ball is thrown from the top of a tower in vertically upward direction. Velocity at a point h m below the point of projection is twice of the velocity at a point h m above the point of projection. Find the maximum height reached by the ball above the top of tower.
View SolutionFrom a tower of height `H`, a particle is thrown vertically upwards with a speed `u` . The time taken by the particle , to hit the ground , is ` n` times that taken by it to reach the highest point of its path. The relative between ` H, u and n` is :
View SolutionA bolloon starts from rest moves vertically upwards with an acceleration `g//8 ms^(-2)` a stone falls from the balloon after 8 s from the start. Further time taken by the stone to reachg the ground `(g=9.8ms^(-2))` is
View SolutionA passenger is standing `d` metres away from a bus. The bus begins to move eith constat acceleration `a. To catch the bus the passenger runs at a constant speed (v) towards the bus, at what minimum speed he must have ,so that he may catch the bus.
View SolutionTwo trains, each travelling with a speed of `37.5kmh^(-1)` are approaching each other on the same straingh track. A bird that can fly at 60 kmph flies off from one train when they are 90 km apart and heads directly for the other train. On reaching the other train, it flies back to the first and so on. total distance covered by the bird before trains collide is
View SolutionOn a two lane road , car (A) is travelling with a speed of `36 km h^(-1)`. Tho car ` B and C` approach car (A) in opposite directions with a speed of ` 54 km h^(-1)` each . At a certain instant , when the distance (AB) is equal to (AC), both being ` 1 km, (B) decides to overtake ` A before C does , What minimum accelration of car (B) is required to avoid and accident.
View SolutionA body is at rest at ` x =0 ` . At ` t = 0`, it starts moving in the positive `x - direction` with a constant acceleration . At the same instant another body passes through ` x= 0 ` moving in the positive ` x - direction ` with a constant speed . The position of the first body is given by `x_(1)(t)` after time 't', and that of the second body by ` x_(2)(t)` after the same time interval . which of the following graphs correctly describes `(x_(1) - x_(2))` as a function of time 't' ?
View SolutionA particle has an initial velocity of `3hat(i) + 4 hat(j)` and an acceleration of `0.4 hat(i) + 0.3 hat(j)`. Its speed after `10s ` is :
View Solution
Examples questions and complete solutions for chapter MOTION IN A STRAIGHT LINE of NARAYANA PHYSICS (HINGLISH) of Class 11