Complete Solutions to Single answer type of chapter COLLISION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | COLLISION |
| NARAYANA | Single answer type |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |

A board is moving with velocity `v` on a smoother horizontal plane. The upper surface of the board is rough on which a ball falls with velocity `v` and rebounds with velocity `(v)/(2)`. The mass of the board is same as that of ball. After the collision, the board comes to state of rest. The co-efficient of friction between the board and the ball is
View SolutionTwo balls of masses `m_(1)` and `m_(2)` are placed on top of one over the other (with a small gap between them) and then dropped on to the ground. What is the ration `m_(1)//m_(2)` for which the upper ball ultimately receives the largest possible fraction of the total energy? Take all collisions as elastic. Neglect air resistance

View SolutionA `20 ` gm bullet pierces through a plate of mass `m_(1) = 1` kg and then comes to rest inside a second plate of mass `M_(2) = 2.98` kg as shown , it is found that the two plates initily atrest , now move with equal velocity . Find the percentage loss in the initial velocity of the bullet when it is between `M` and `M_(2)` neglet any loss of material of the pletes due to the action of the bullet
View SolutionThe air of density `rho` and moving with a velocity `v` strikes perpendicular the inclined surface of area `A` and of a wedge kept on a horizontal surface. The mass of the wedge is `m`. Assuming the collisions to be perfectly inelastic, the minimum value of the coefficient of friction between the wedge and the ground so that the wedge does not move is (Assume mass of particles of air is negligible)

View SolutionTwo identical ball of radii `r` are kept on a horizontal plane with their centres `d` distance apart. A third ball, identical to previous one, collide elastically with both the balls symmetrically as shown in the figure. If the third ball comes to rest after the collision, `d` should be

View SolutionA partical of mass `m` moving with velocity `1m//s` collides perfectly elastically with another particle of mass `2m`. If the incident particle is deflected by `90^(circ)`. The heavy mass will make and angle `theta` with the initial direction of `m` equal to:
View SolutionMass `m_(1)` strikes `m_(2)` which is at rest. The ratio of masses for which they will collide again. (Collisions between ball and wall are elastic. Coefficient of resttution between `m_(1)` and `m_(2)` is `e` and all the surface are smooth)

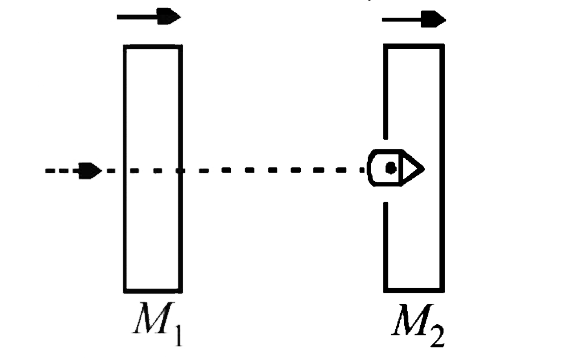
View SolutionA smooth washer impinges at a velocity `'v'` on a group of three smooth identical blocksresting on a smooth horizontal surface as shown in fig. Mass of each block is equal to mass of the washer. The diameter of the washer and its height are equal to edge of the block. The velocity of blocks `(2)` and `(3)` after collision is
View SolutionA partical of mass `'m'` moving with a velocity `(3 hat(i)+2hat(j))m//s` collides with statinary mass `'M'` and finally `'m'` moves with a velocity `(-2hat(i)+hat(j))m//s` if `(m)/(M) = (1)/(13)` the velocity of the `M` after collision is?
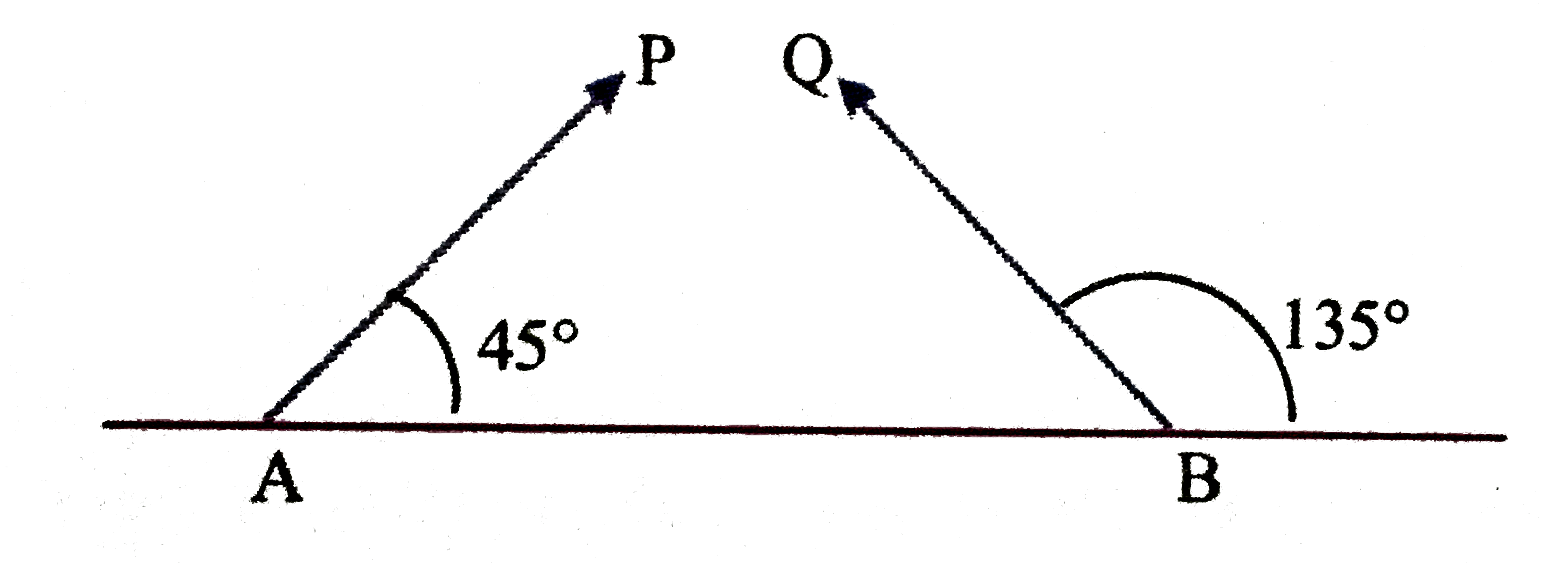
View SolutionParticles `P` and `Q` of masses `20g` and `40g`, respectively, are projected from positions `A` and `B` on the ground. The initial velocities of `P` and `Q` make angles of `45^(circ)` and `135^(circ)`, respectively with the horizontal as shown in the fig. Each particle has an initial speed of `49m//s`. The separation `AB` is `245m`. Both particles travel in the same vertical plane and undergo a collision. After the collision `P` retraces its path. The separation of `Q` from its initial position when it hits the ground is
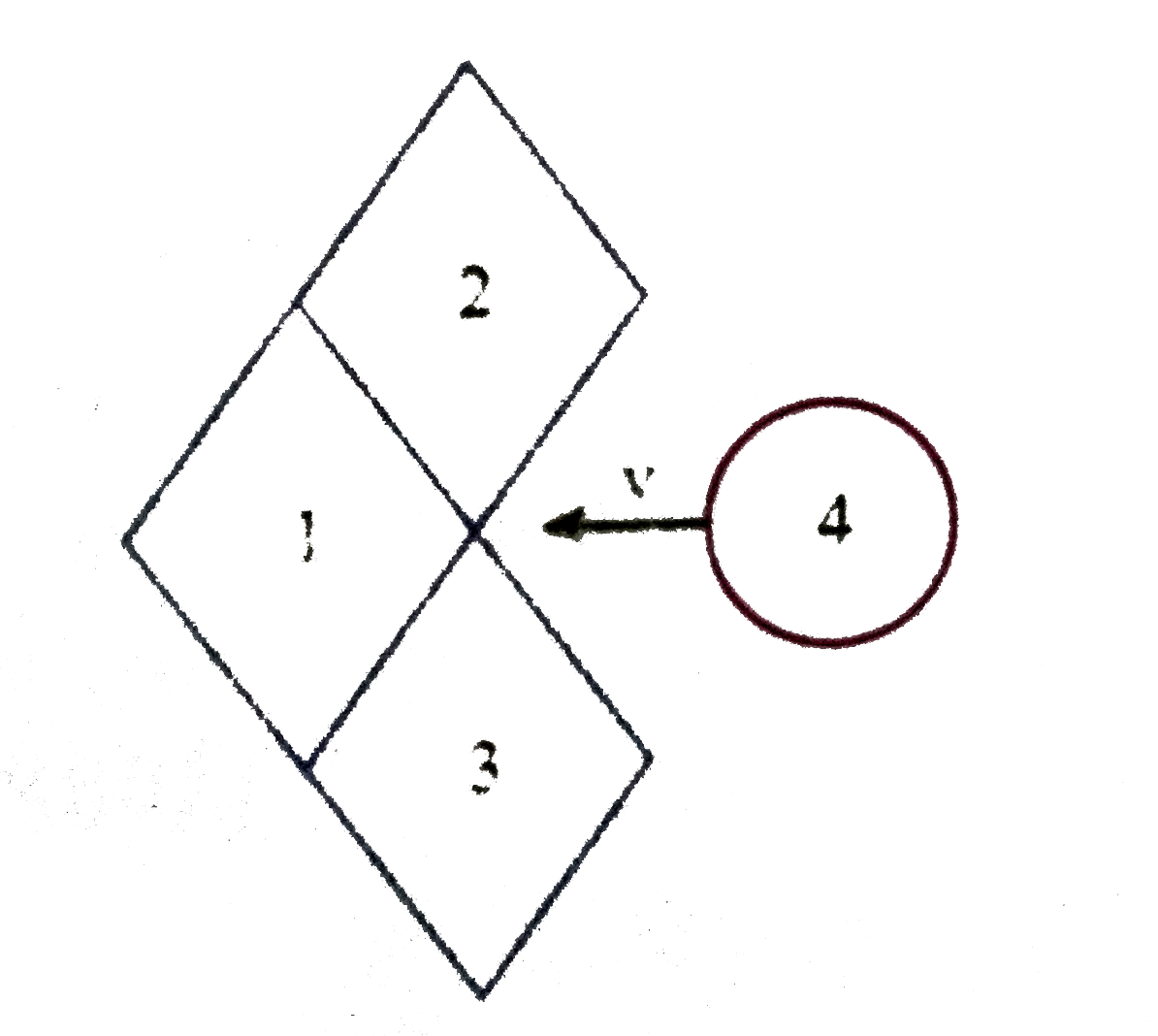
View SolutionTwo small particles of equal masses stant moving in opposite direction from a point `A` in a burtizonetal circule orbic their tangention velocity are `V` and `2V` , respectively as shown in the figure between collsions , the particals move with constant speed After making how many elastic collition , other the then that at `A` these two partical will again reach the point `A` ?

View SolutionBlock `A` is hanging from vertical spring of spring constant `K` and is rest. Block `B` strikes block `A` with velocity `v` and sticks to it. Then the value of `v` for which the spring just attains natural length is
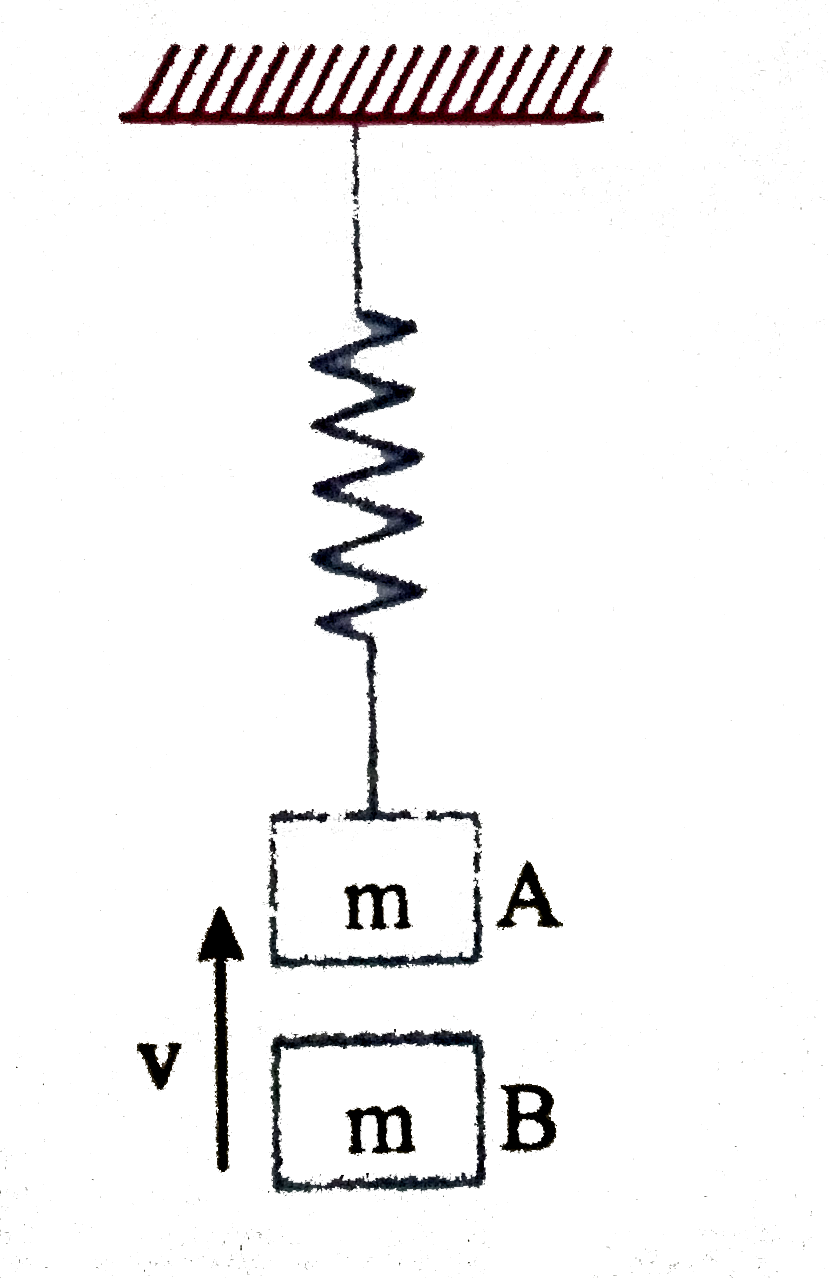
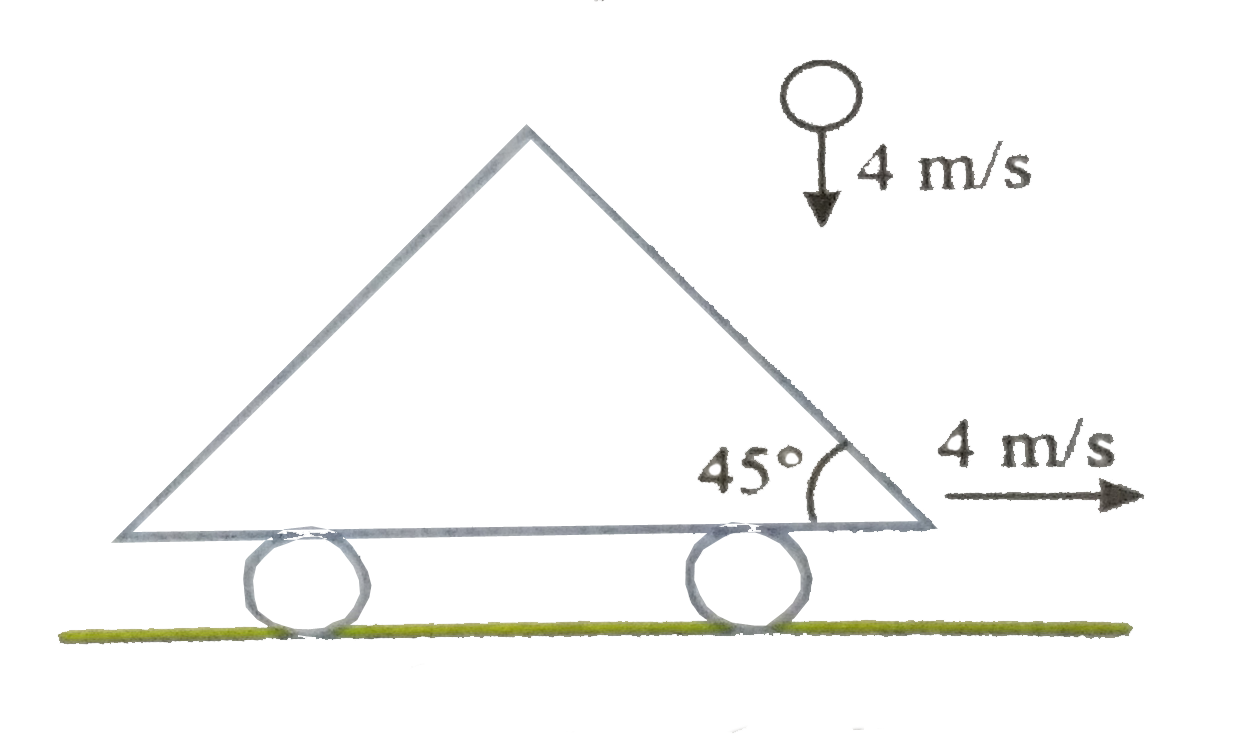
View SolutionA small ball falling vertically downward with constant velocity `4m//s` strikes elastically a massive inclined cart moving with velocity `4m//s` horizontally as shown. The velocity of the rebound of the ball is
View SolutionA spaceship travelling along `+y` axis with speed `v_(0)` suddenly shoots out one fourth of its parts with speed `2v_(0)` along `+x`-axis. `xy` axes are fixed with respect to ground. The velocity of the remaining part is
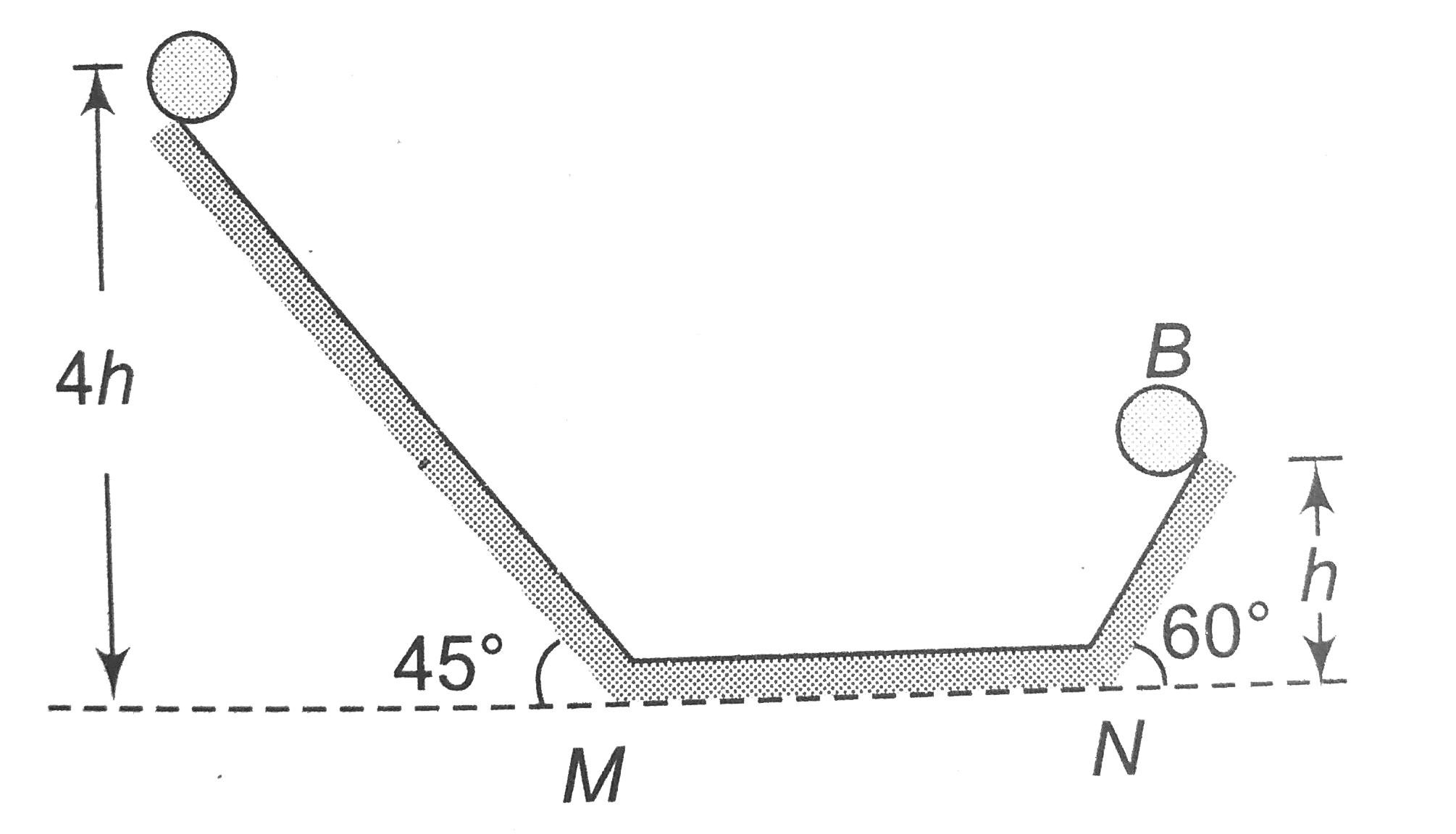
View SolutionTwo identical balls `A and B` arereleased from the positions shown in figure. They collide elasticallly on horizontal position `MN` . The ratio of the heightsattaned by `A and B` after collisuion will be (neglect friction):
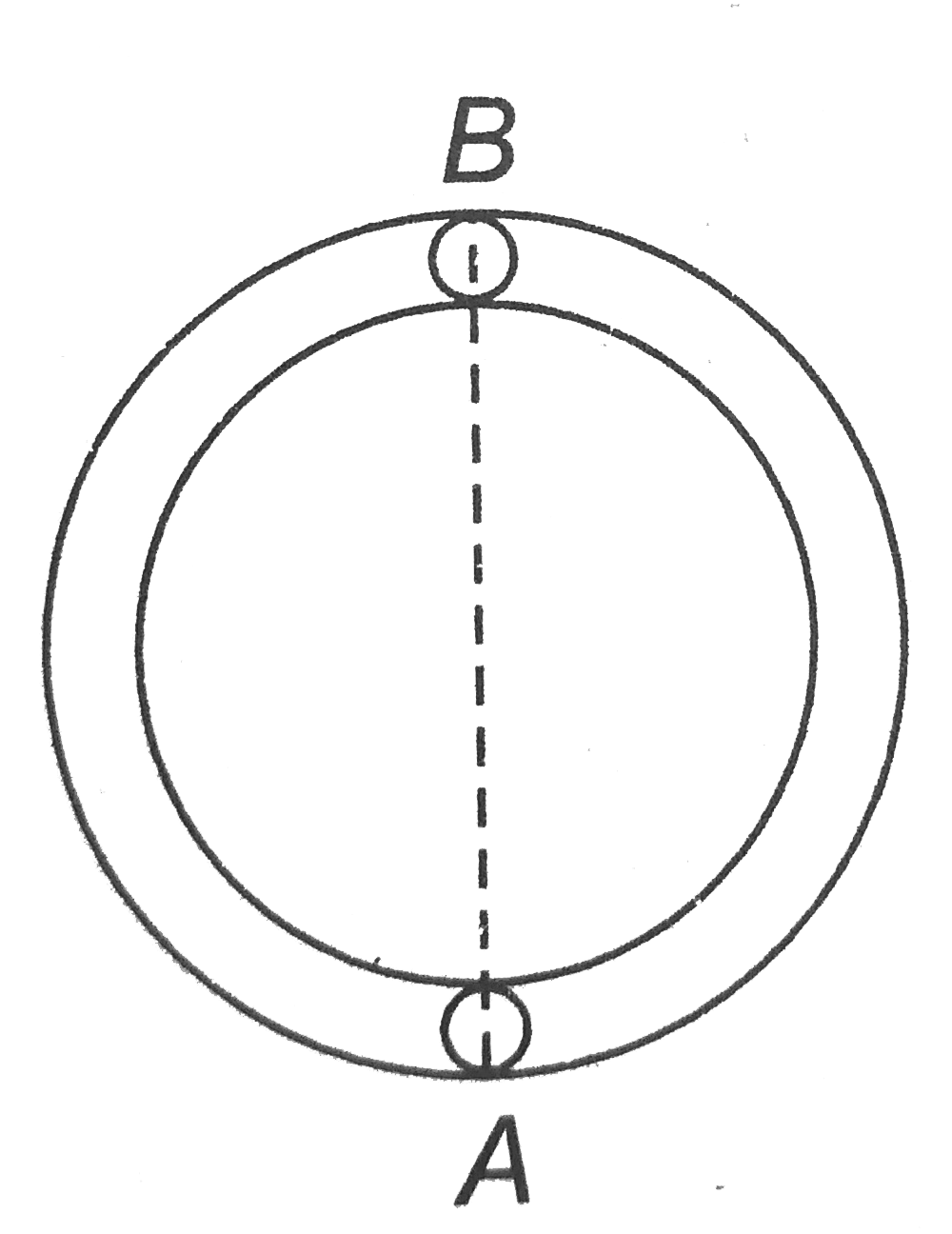
View SolutionTwo equal sphere `A and b` lie on a smooth horizontal circle groove at opposite ends of a diameter. At time `t= 0,A` is projected along the groove and tis first implings on`B` at time `t = T_(1) and again at time `t = T_(2)`. If `e` is the coefficient of restitution, the ratio `T_(2)//T_(1)` is
View SolutionA ball of mass `10 kg` strikes another ball of mass `25 kg` at rest. If they separated in mutually perpendicular directions then the coefficient of restitution is:
View SolutionThe coefficient of restitution for a body is `e=(1)/(3)`. At what angle the body must be incident on a perfectly hard plane so that the angle between the direction before and after the impact be at right angles:
View SolutionAn iron ball of mass `m`, suspeneded by a light inextensible string of length `l` from a fixed point `O`, is shifted by an angle `._(0)` as shown so as to strike the vertical wall perpendicularly. The maximum angle made by the string with vertical after the first collision ( `e` is the coefficient of restitution). is_______

View SolutionThree small bodies with the mass ratio 3 : 4: 5 (the mass of the lightest body is m) are kept at three different points on the inner surface of a smooth hemispherical cup of radius r. The cup is fixed at its lowest point on a horizontal surface. At a certain instant, the bodies are released. Determine the maximum amount of heat Q that can be liberated in such a system.At what initial arrangement of the bodies will the amount of liberated heat be maximum ? Assume that collisions are perfectly inelastic.
View Solution
Single answer type questions and complete solutions for chapter COLLISION of NARAYANA PHYSICS (HINGLISH) of Class 11