An iron ball of mass m, suspeneded by a light inextensible string of length l from a fixed point O, is shifted by an angle .0 as shown so as to strike the vertical wall perpendicularly. The maximum angle made by the string with vertical after the first collision ( e is the coefficient of restitution). is_______

sin−1{1−e2(1−cosθ0)}
cos−1{1−e2(1−cosθ0)}
Tan−1{1−e2(1−cosθ0)}
Zero
The correct Answer is:B
Speed just before collision =√2gl(1−cos.0)
Speed just after collosion : e√2gl(1−cos.0)
from conservation of energy,
12me2[2gl(1−cos.0)]=mgl(1−cos.)
∴.=cos−1{1−e2(1−cos.0)}
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - COLLISIONEXERCISE - INTEGER TYPE QUESTIONS8videos
COLLISION
- BOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Multiple Answer11videos
COLLISION
- BOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL II(H.W)51videos
CIRCULAR MOTION
- BOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I6videos
FRICTION
Similar Questions
A bob of mass m suspended by a light inextensible string of length 'l' from a fixed point. The bob is given a speed of √6gl. Find the tension in the string when string deflects through an angle 120∘ from the vertical.
View SolutionA steel ball is suspended by a light in extensible string of length l from a fixed point O. When the ball is in equilibrium it just touches a vertical wall as shown in the figure. The ball is first taken aside such that string becomes horizontal and then released from rest. If coefficient of restitution is e, then find the maximum deflection of the string after nth collision.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
An iron ball of mass m, suspended by a light inextensible string of length l from a fixed point O, is shifted by θ0 as shown so as to strike the vertical wail perpendicularly.The maximum angle made by the string with vertical after the first collision, if e is the coefficient of restitution, is
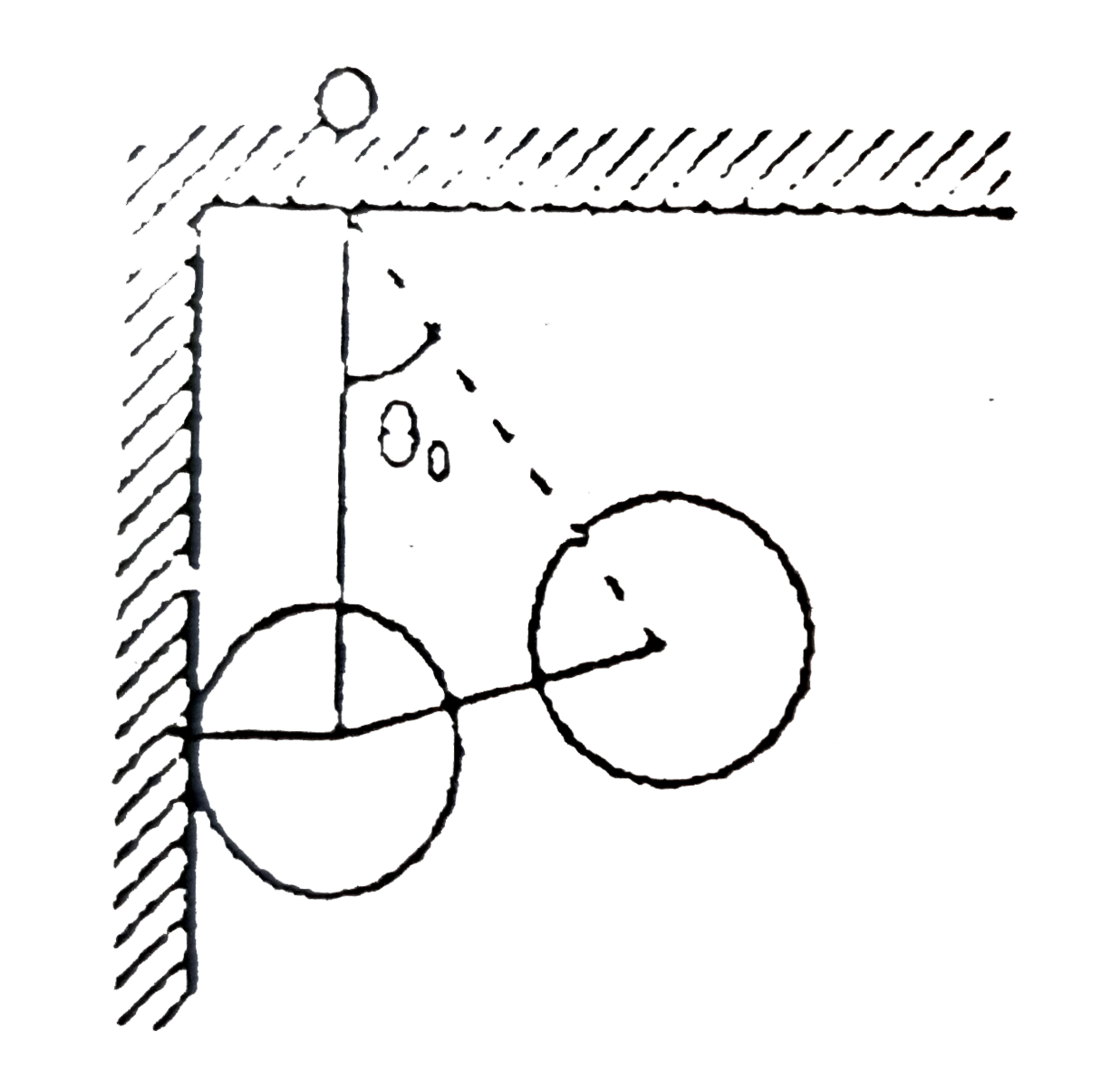 Asin−1{1−e2(1−cosθ0)}Bcos−1{1−e2(1−cosθ0)}Ctan−1{1−e2(1−cosθ0)}Dzero
Asin−1{1−e2(1−cosθ0)}Bcos−1{1−e2(1−cosθ0)}Ctan−1{1−e2(1−cosθ0)}Dzero - Question 2 - Select One
A particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl

The maximum angle made by the string with downward vertical isAcos−1(14)Bsin−1(14)Cπ2+cos−1(14)Dπ−cos−1(14) - Question 3 - Select One
A heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
A√31g,cos−1(3/2)B√1g3,cos−1(2/3)C√3g3,cos−1(2/3)D√gl3,cos−1(2/3)
A bob of mass m is suspended by a light inextensible string of length l from a fixed point such that it is free to rotate in a vertical plane. The bob is given' a speed of √4gl horizontally. The, height of the bob from the lower most point where the string just becomes slacked is nl3. Find n.
View SolutionA particle of mass m is suspended by a string of length l from a fixed rigid support. Particle is imparted a horizontal velocity u=√2gl. Find the angle made by the string with the vertical when the acceleration of the particle is inclined to the string by 45∘?
View SolutionA particle of mass m is suspended by a string of length l from a fixed rigid support. A sufficient horizontal velocity =√3gl is imparted to it suddenly. Calculate the angle made by the string with the vertical when the accekleration of the particle is inclined to the string by 45∘ .
View SolutionA ball A of mass m attached to a string of length L is released when the string is horizontal. It strikes another ball B of mass 2m suspended to another string of length L at rest as shown. Find the maximum angle made by the string if the collision is completely inelastic.
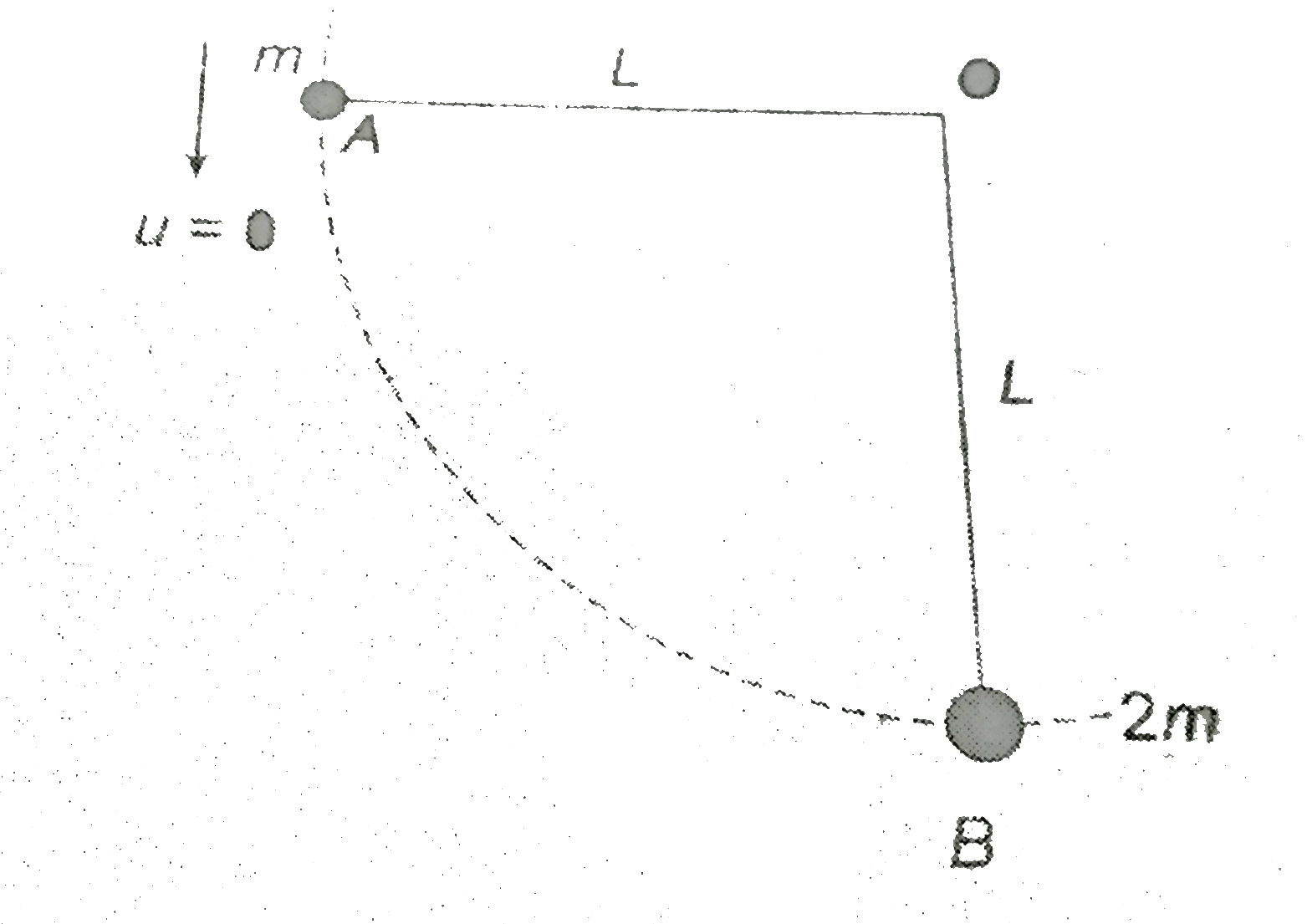 View Solution
View SolutionA ball is hanging vertically by a light inextensible string of length L from fixed point O. The ball of mass m is given a speed u at the lowest position such that it completes a vertical circle with centre at O as shown. Let AB be a diameter of circular path of ball making an angle θ with vertical as shown. (g is acceleration due to gravity)
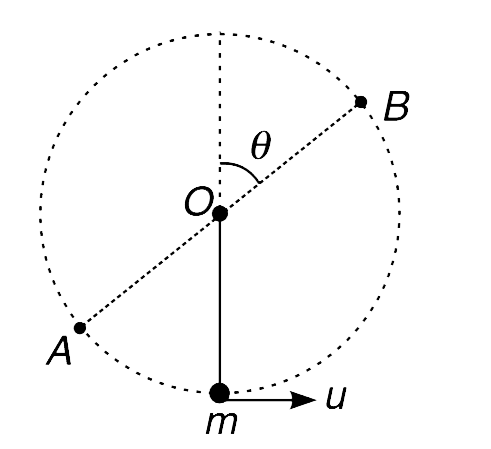
a) Let TA and TB be tension in string when ball is at A and B respectively, then find TA – TB. (b) Let →aA and →aB be acceleration of ball when it is at A and B respectively, then find the value of |→aA+→aB|View Solution

