Complete Solutions to Comprehension type of chapter COLLISION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | COLLISION |
| NARAYANA | Comprehension type |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
A small ball is projected at an angle `alpha` between two vertical walls such that in the absence of the wall its range would have been `5d`. Given that all the collisions are perfectly elastic, find.
(a) maximum height atained by the ball.
(b) total number of collisions with the walls before the ball comes back to the ground, and
(c) point at which the ball finally falls. The walls are supposed to be very tall.

View SolutionA small ball is projected at an angle `alpha` between two vertical walls such that in the absence of the wall its range would have been `5d`. Given that all the collisions are perfectly elastic, find.
(a) maximum height atained by the ball.
(b) total number of collisions with the walls before the ball comes back to the ground, and
(c) point at which the ball finally falls. The walls are supposed to be very tall.

View SolutionSuppose a ball is projected with speed `u` at an angle `alpha` with horizontal. It collides at some distance with a wall parallel to y-axis.
Let `v_(x)` and `v_(y)` be the components of its velocity along `x` and y-directions at the time of impact with wall. Coefficient of restitution between the ball and the wall is `e`. Component of its velocity along `y`-diection (common tangent) `v_(y)` will remain unchanged while component of its velocity along `x` -direction (common normal) `v_(x)` will become `ev_(x)` is opposite direction.
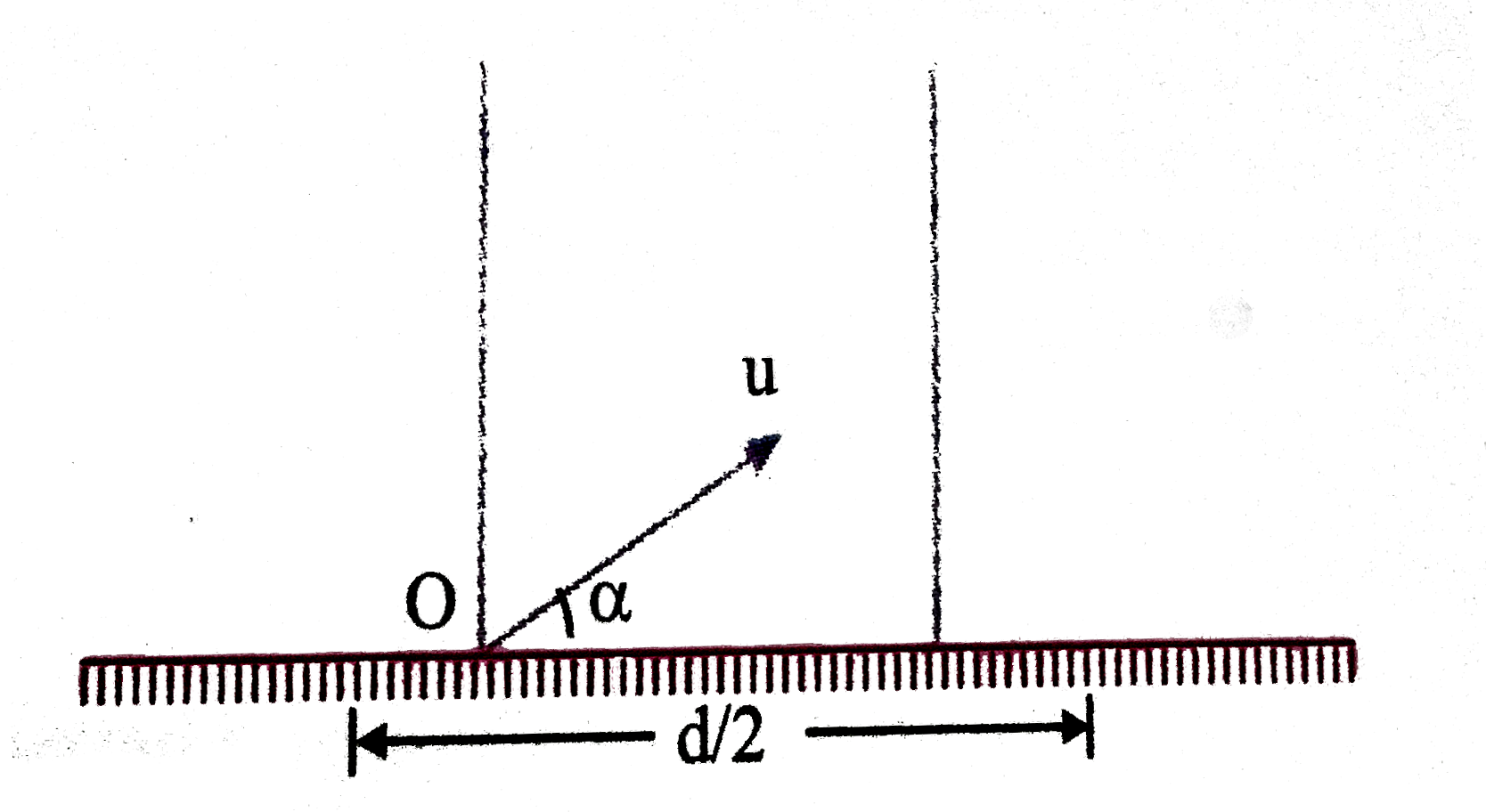
The situation shown in the figure a small ball is projected at an angle `alpha` between two vertical walls such that in the absence of the wall its range would have been `5d`. Given that all the collisions are perfectly elastic (for first and second problems), the walls are supposed to be very tall.
The total time taken by the ball to come back to the ground (if collision is inelastic) is
View SolutionTwo pendulum bobs of mass `m` and `2m` collide elastically at the lowest point in their motion. If both the balls are releasd from height `H` above the lowest point,
Velocity of the bob of mass `m` just after collision is
View SolutionTwo pendulum bobs of masses m and 2m collide head on elastically at the lowest point in their motion. If both the balls are released from a height H above the lowest point, to what heights do they rise for the first time after collision?
View SolutionTwo pendulum bobs of masses m and 2m collide head on elastically at the lowest point in their motion. If both the balls are released from a height H above the lowest point, to what heights do they rise for the first time after collision?
View SolutionA light in extensible thread passes over a small frictionless pully. Two blocks of masses `m = kg` and `M = 3kg` respectively are attached with the thread as shown in the fig. The heavier block rests on a horizontal surface. A shell of mass `1 kg` moving upward with a velocity `10m//s` collides and sticks with the block of mass `'m'` as shown in the fig at `t = 0`. If the long inclined plane is smooth.
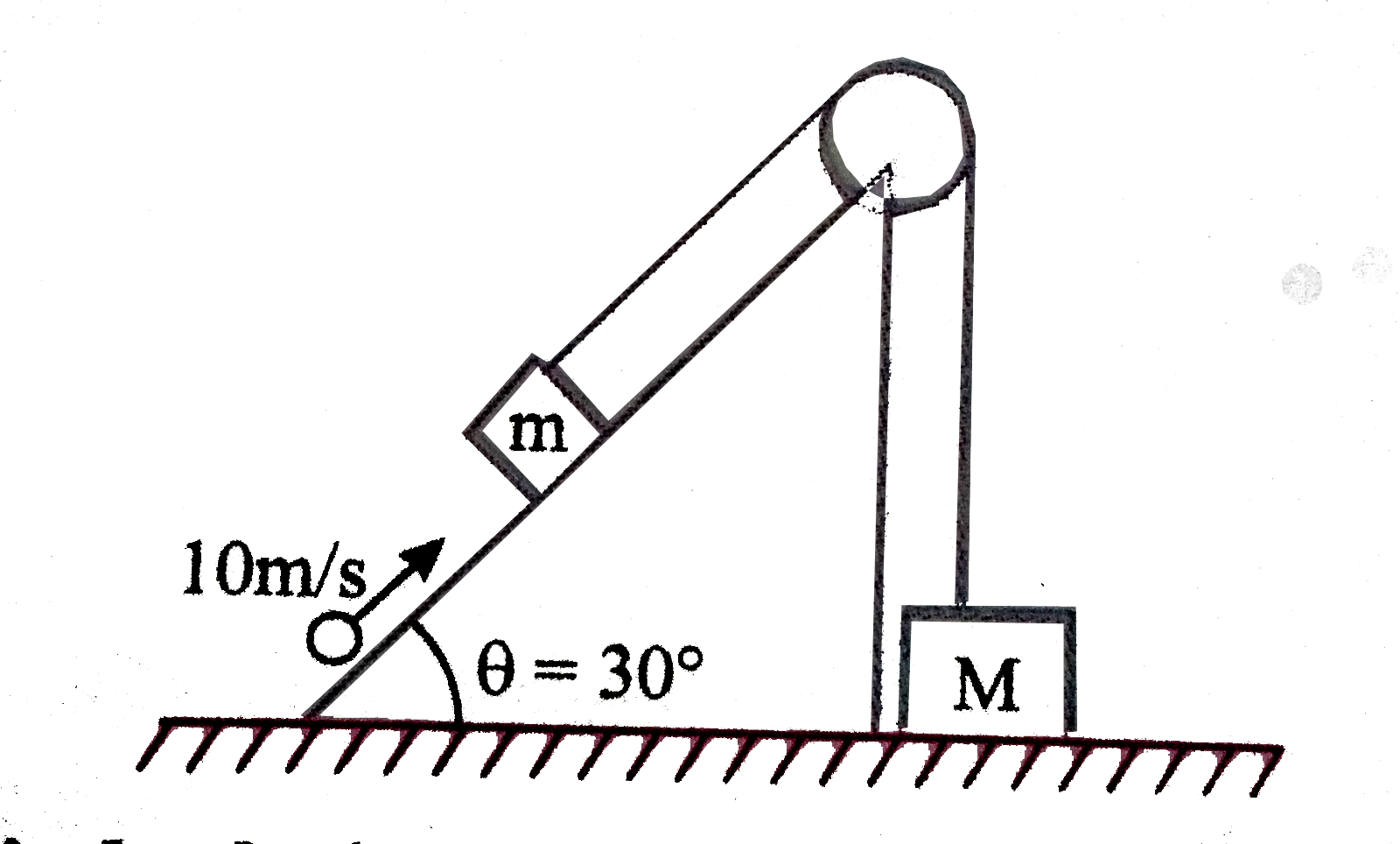
Find velocity of `(m+"shell")` just after collision.
View SolutionA light in extensible thread passes over a small frictionless pully. Two blocks of masses `m = kg` and `M = 3kg` respectively are attached with the thread as shown in the fig. The heavier block rests on a horizontal surface. A shell of mass `1 kg` moving upward with a velocity `10m//s` collides and sticks with the block of mass `'m'` as shown in the fig at `t = 0`. If the long inclined plane is smooth.
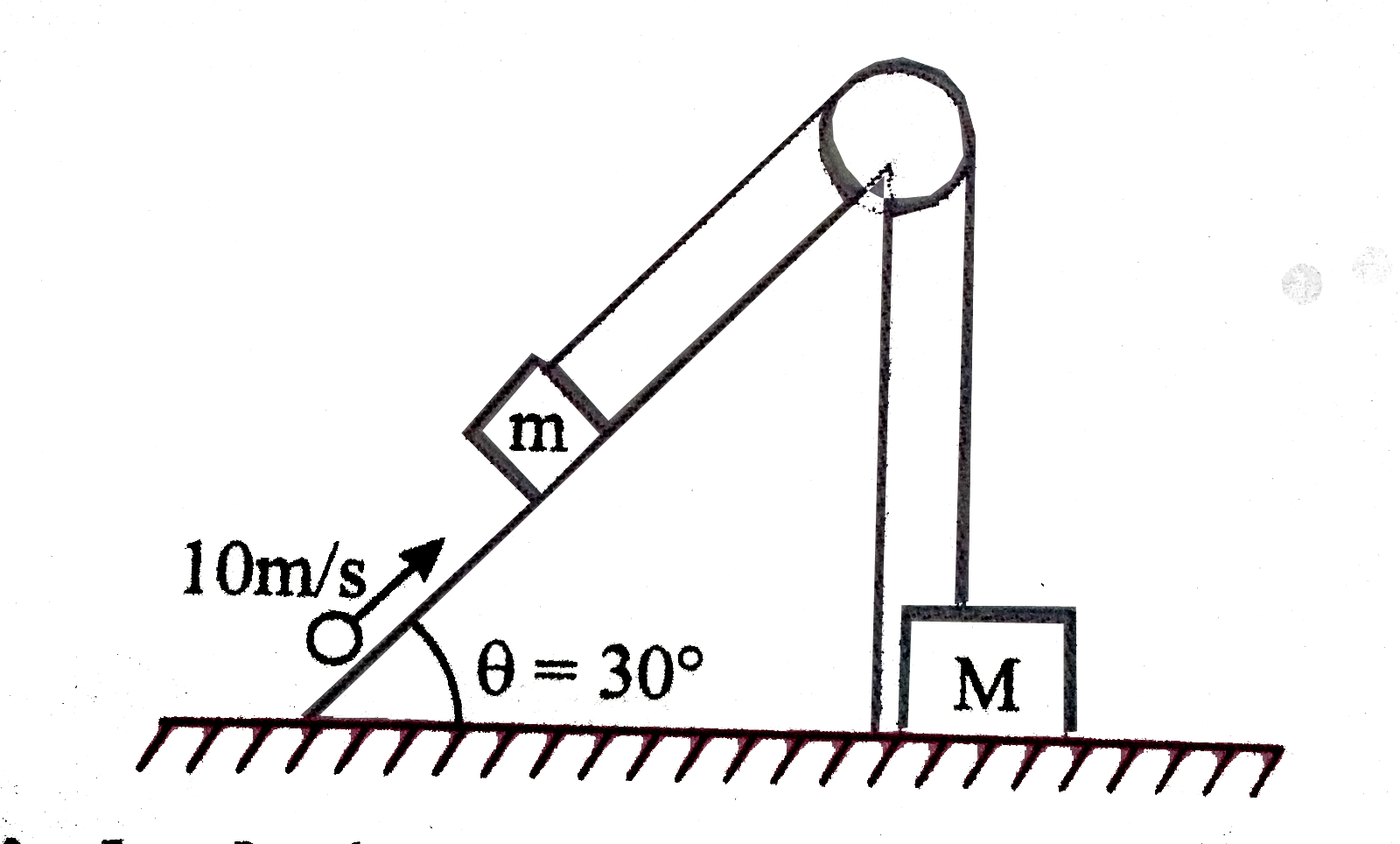
Find the maximum height ascended by `'M'`
View SolutionA light in extensible thread passes over a small frictionless pully. Two blocks of masses `m = kg` and `M = 3kg` respectively are attached with the thread as shown in the fig. The heavier block rests on a horizontal surface. A shell of mass `1 kg` moving upward with a velocity `10m//s` collides and sticks with the block of mass `'m'` as shown in the fig at `t = 0`. If the long inclined plane is smooth.
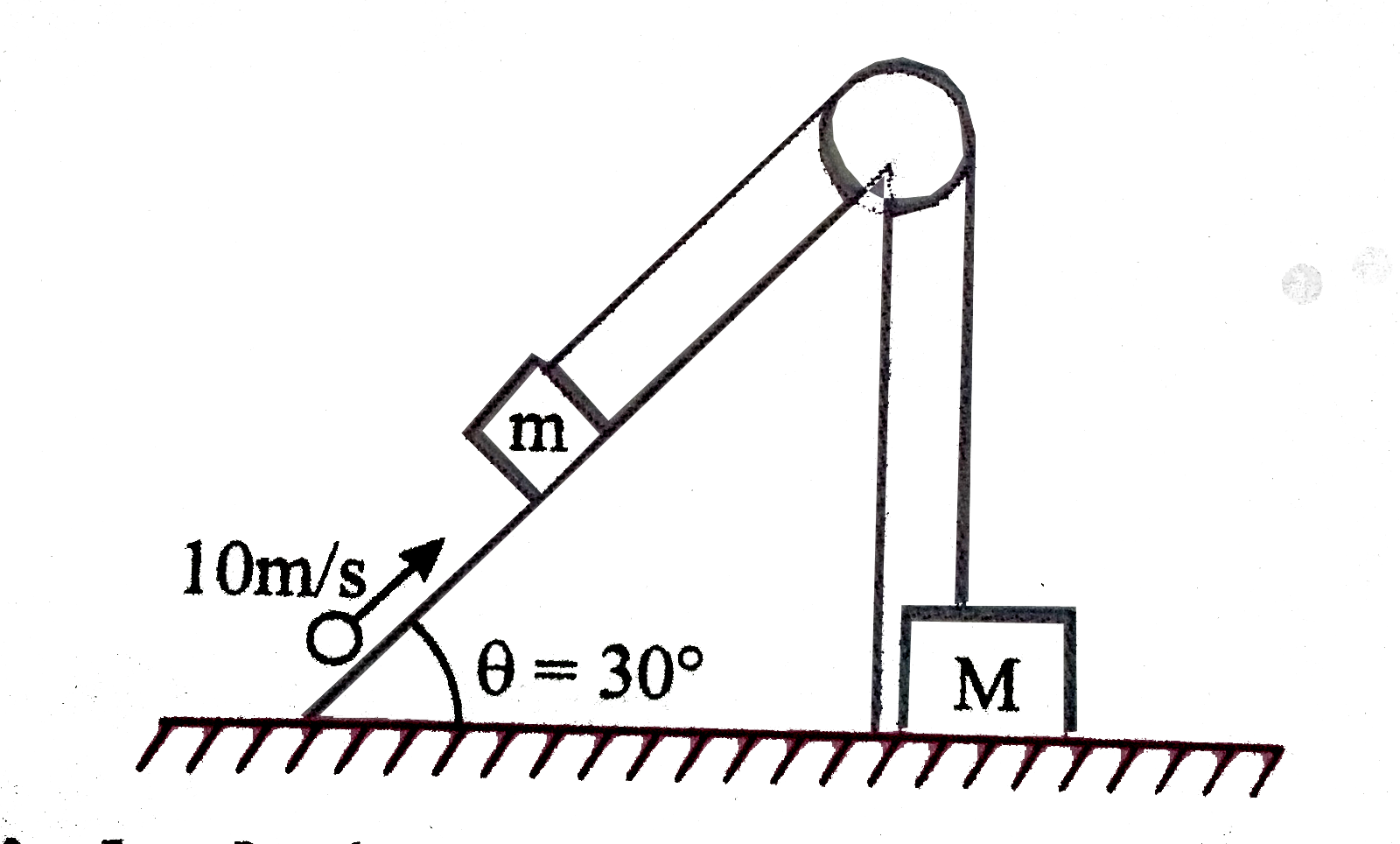
Find the total time `T` at that instant of maximum height ascended by `M`
View SolutionWedges `B` and `C` are smooth and they are placed in contact as shown. Block `A` is placed on wedge `B` at a height `h` above ground. Block and the two wedges are all of same mass `m`. Neglect friction every where.
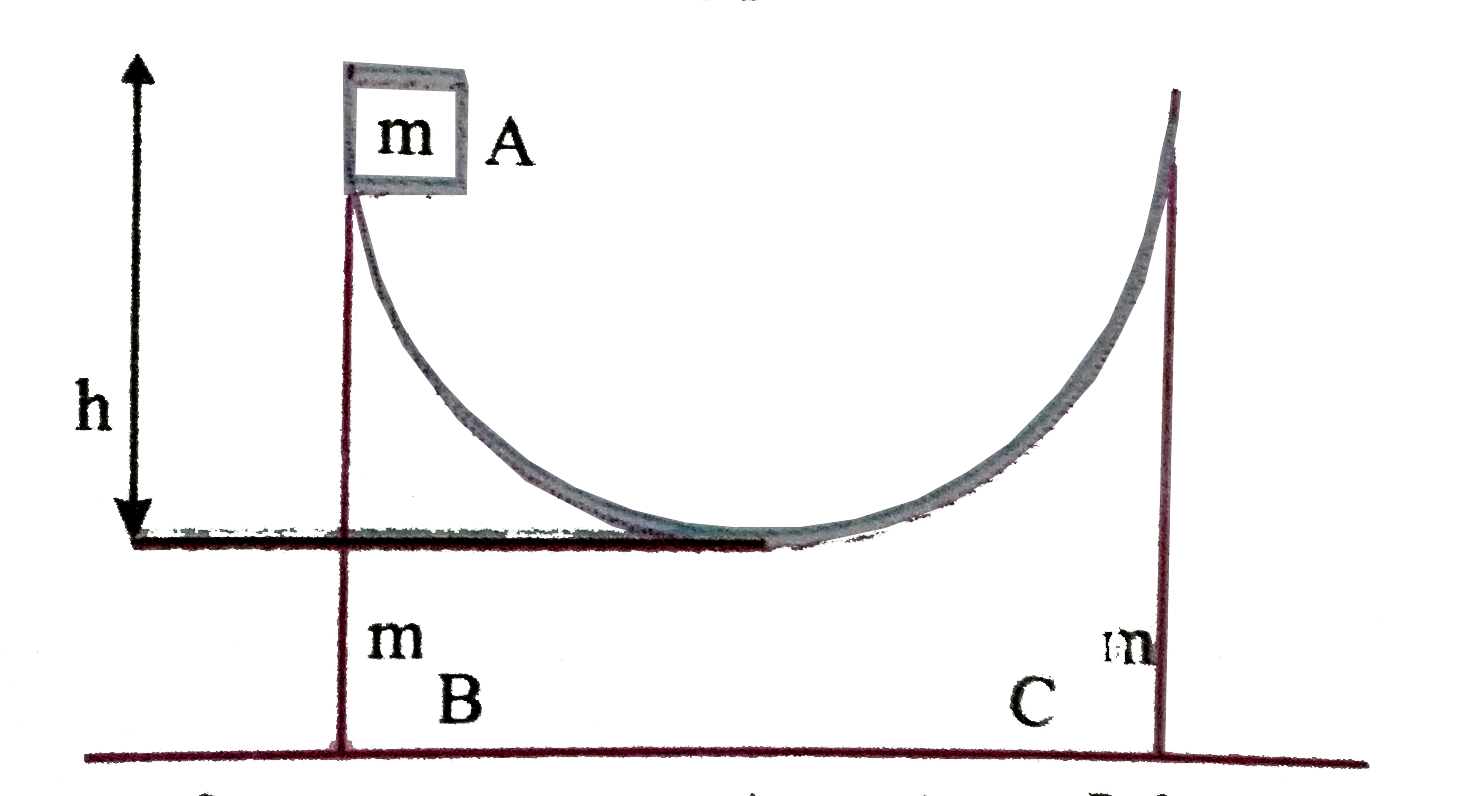
The maximum height upto which block `A` rises on wedge `C` is
View SolutionWedges `B` and `C` are smooth and they are placed in contact as shown. Block `A` is placed on wedge `B` at a height `h` above ground. Block and the two wedges are all of same mass `m`. Neglect friction every where.
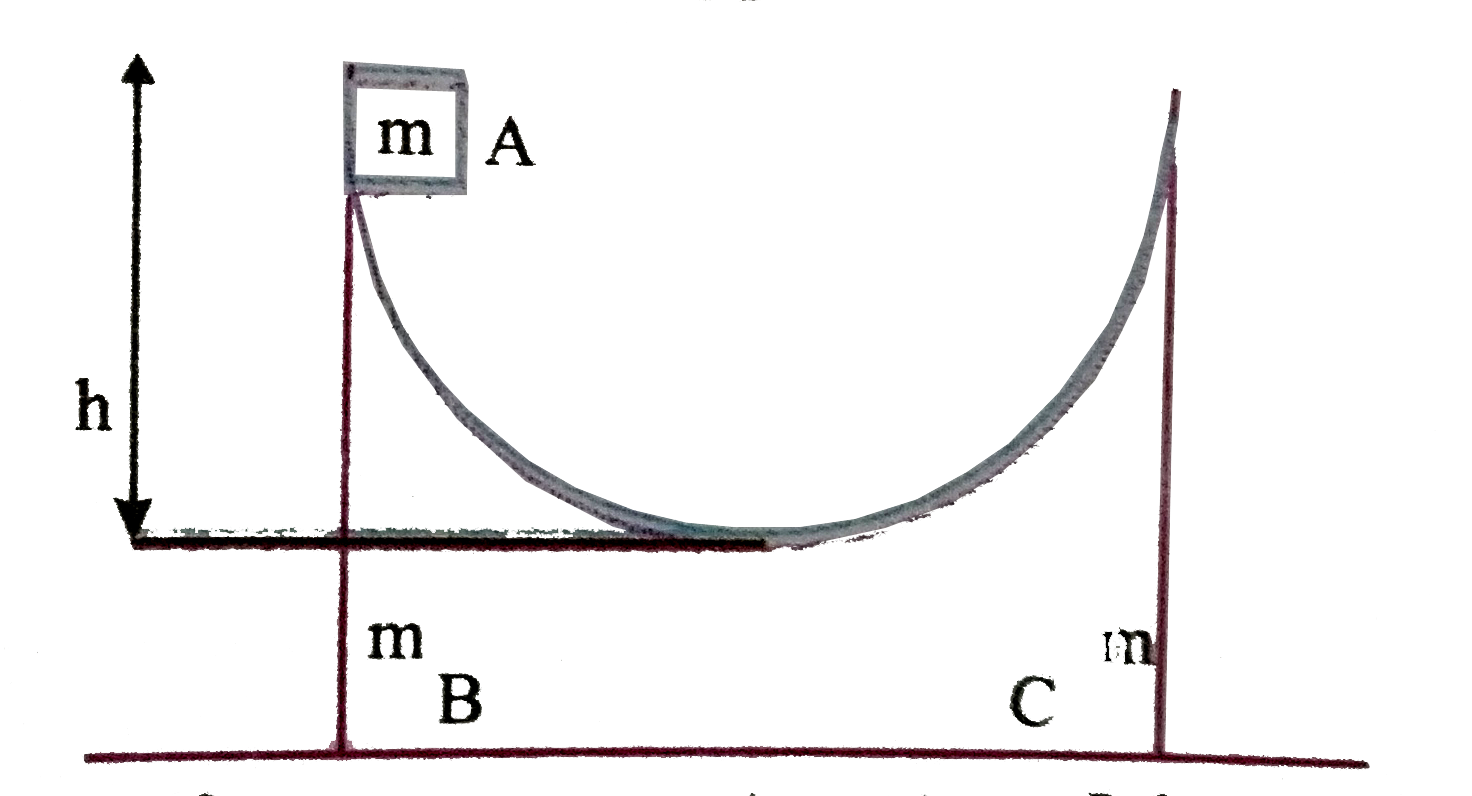
The velocity of `A` when it has slide down to ground from wedge `C` is
View SolutionA uniform bar of length `12 L` and mass `48 m` is supported horizontally on two smooth tables as shown in the figure. A small moth (an insect) of mass `8m` is sitting on end `A` of the rod and a spider (an insect) of mass `16 m` is sitting on the other end `B`. Both the insects start moving towards each other along the rod with moth moving at speed `2v` and the spider at half of this speed. They meet at a point `P` on the rod and the spider eats the moth. After this the spider moves with a velocity `v//2` relative to the rod towards the end `A`. The spider takes negligible time in eating the insect. Also, let `v = L//T`, where `T` is a constant having value `4 sec`.
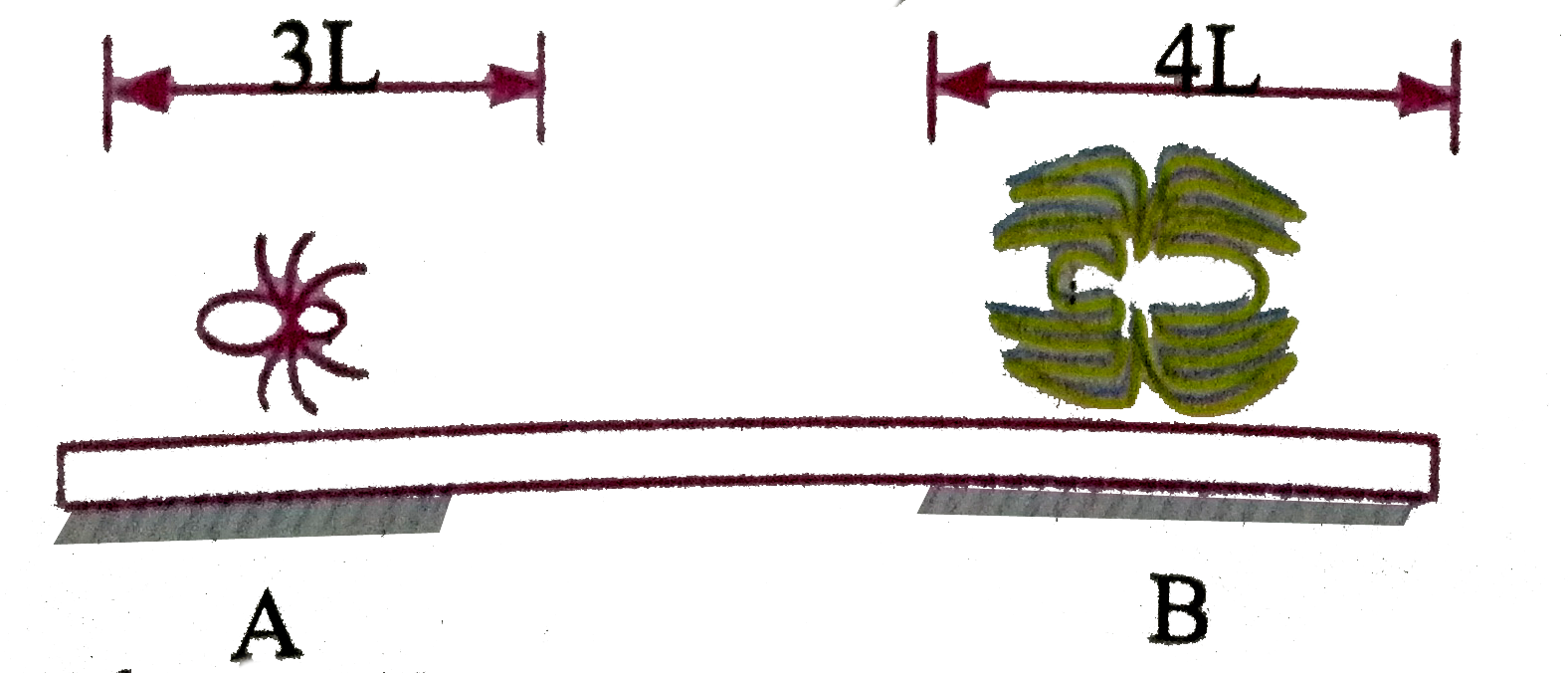
Displacement of the rod by the time when the insects meet is
View SolutionA uniform bar of length `12 L` and mass `48 m` is supported horizontally on two smooth tables as shown in the figure. A small moth (an insect) of mass `8m` is sitting on end `A` of the rod and a spider (an insect) of mass `16 m` is sitting on the other end `B`. Both the insects start moving towards each other along the rod with moth moving at speed `2v` and the spider at half of this speed. They meet at a point `P` on the rod and the spider eats the moth. After this the spider moves with a velocity `v//2` relative to the rod towards the end `A`. The spider takes negligible time in eating the insect. Also, let `v = L//T`, where `T` is a constant having value `4 sec`.
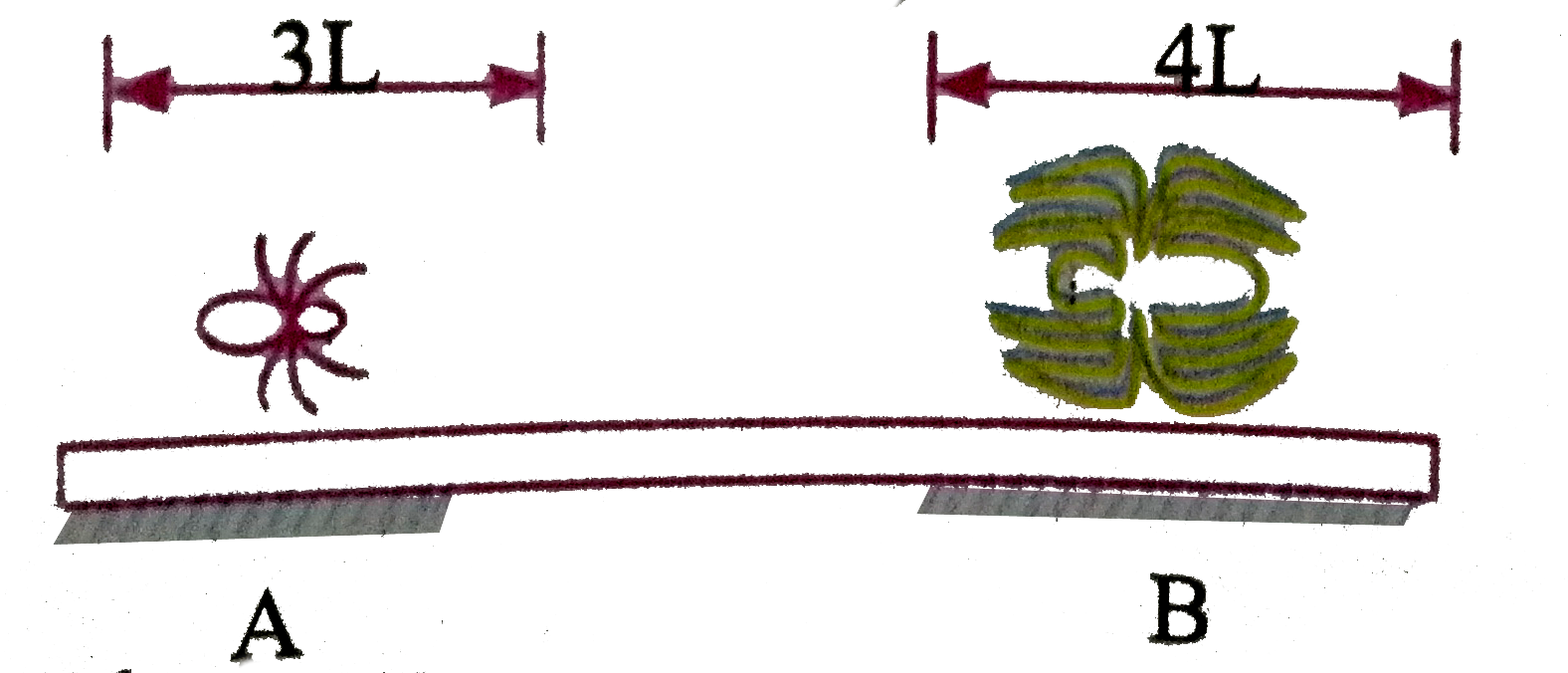
The point `P` is at
View SolutionA uniform bar of length `12 L` and mass `48 m` is supported horizontally on two smooth tables as shown in the figure. A small moth (an insect) of mass `8m` is sitting on end `A` of the rod and a spider (an insect) of mass `16 m` is sitting on the other end `B`. Both the insects start moving towards each other along the rod with moth moving at speed `2v` and the spider at half of this speed. They meet at a point `P` on the rod and the spider eats the moth. After this the spider moves with a velocity `v//2` relative to the rod towards the end `A`. The spider takes negligible time in eating the insect. Also, let `v = L//T`, where `T` is a constant having value `4 sec`.
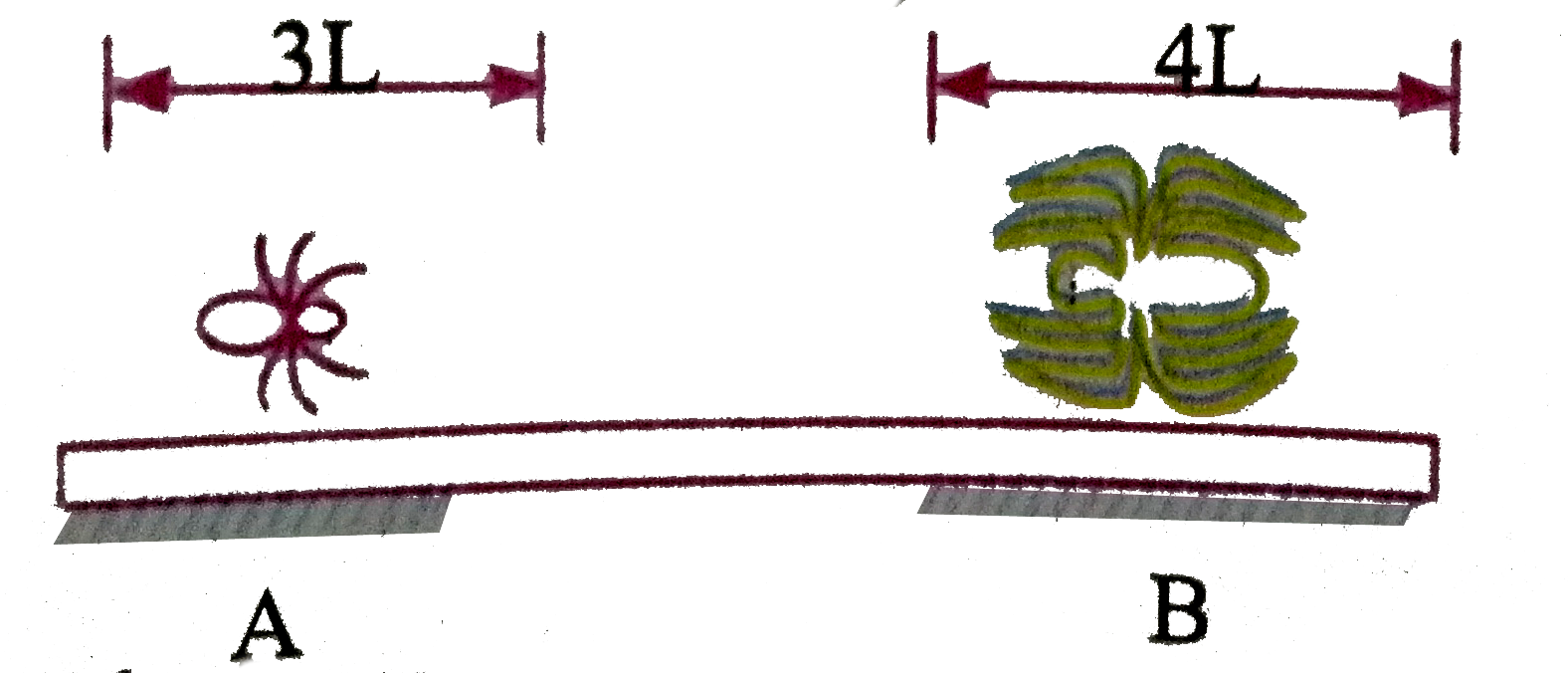
The speed of the bar after the spider eats up the moth and moves towards `A` is
View SolutionA projectile of mass `50 kg` is shot vertically upwards with n initial velocity of `100m//s`. After `5s`, it explodes into two fragments, one of (1st fragment) which having a mass of `20 kg` travels vertically up with a velovity of `150m//s (g = 10 m//s^(2))`. Bases on the above paragraph answer the following questions.
What is the magnitude and direction of velocity of the 2nd fragments just after explosion is
View SolutionA projectile of mass `50 kg` is shot vertically upwards with n initial velocity of `100m//s`. After `5s`, it explodes into two fragments, one of (1st fragment) which having a mass of `20 kg` travels vertically up with a velovity of `150m//s (g = 10 m//s^(2))`. Bases on the above paragraph answer the following questions.
What is the linear momentum of `2nd` fragement `3s` after the explosion is
View SolutionA projectile of mass `50 kg` is shot vertically upwards with n initial velocity of `100m//s`. After `5s`, it explodes into two fragments, one of (1st fragment) which having a mass of `20 kg` travels vertically up with a velovity of `150m//s (g = 10 m//s^(2))`. Bases on the above paragraph answer the following questions.
The sum of linear momenta of fragments `3s` after the explosion is
View SolutionA small particle of mass `m//10` is moving horizontally at a height of `3R//2` from ground with velocity `10m//s`. A perfectly inelastic collision occurs at point `P` of surface. The mass `m` of sphere is `R`. (`m = 10 Kg` and `R = 0.1 m`) (Assume all surfaces to be smooth). Answer the following questions.

speed of particle just after collisons is approximately..........
View SolutionA small particle of mass `m//10` is moving horizontally at a height of `3R//2` from ground with velocity `10m//s`. A perfectly inelastic collision occurs at point `P` of surface. The mass `m` of sphere is `R`. (`m = 10 Kg` and `R = 0.1 m`) (Assume all surfaces to be smooth). Answer the following questions.

Speed of shpere just after collision is
View SolutionTwo smooth balls `A` and `B`, each of mass `m` and radius `R`, have their centres as shown in fig. Ball `A`, moving along positive x-axis, collides with ball `B`. Just before the collision, speed of ball `'A'` is `4m//s` and ball `'B'` is stantionary. The collision
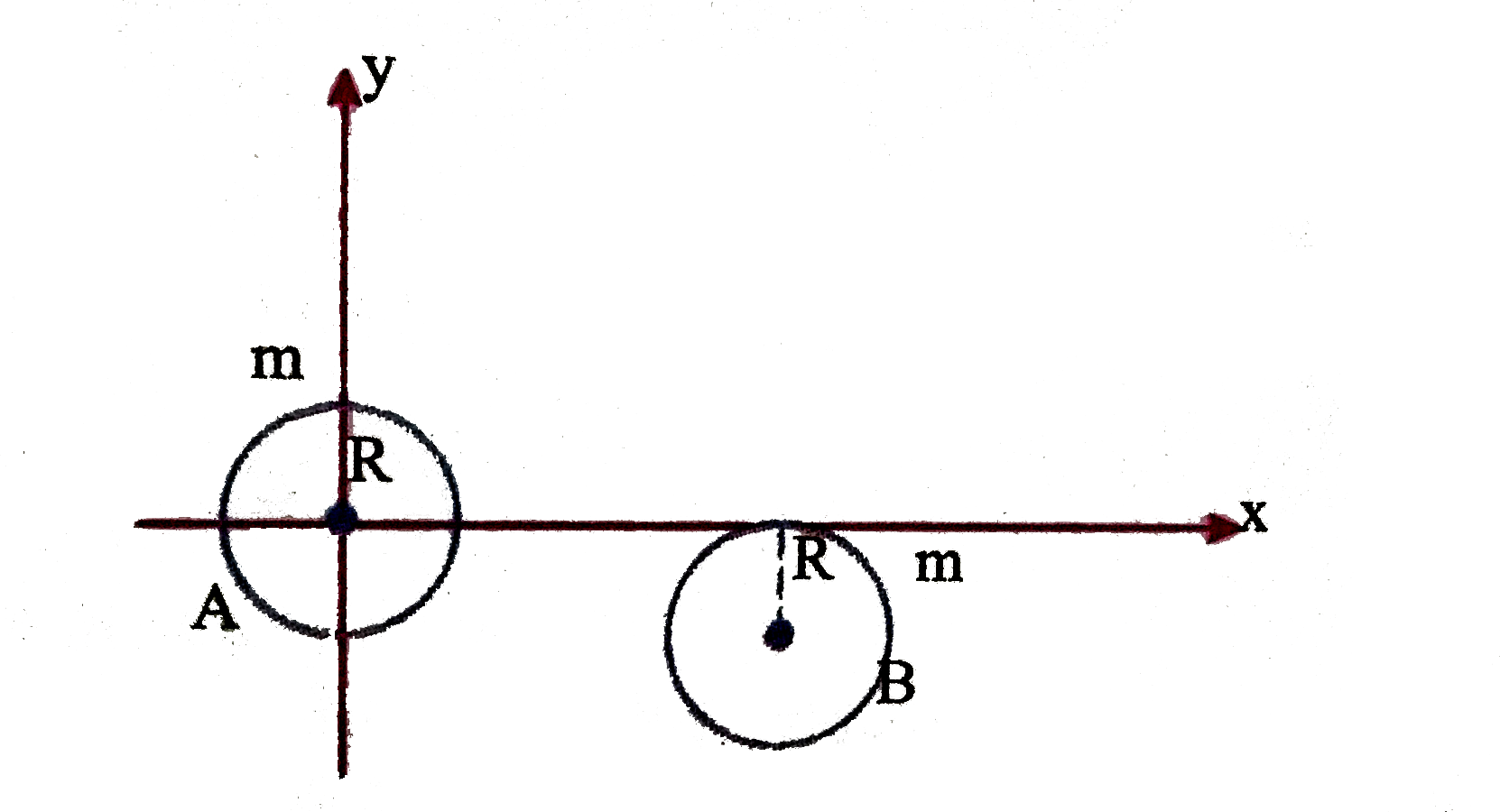
Velocity of the ball `'A'` just after the collision is
View SolutionTwo smooth balls `A` and `B`, each of mass `m` and radius `R`, have their centres as shown in fig. Ball `A`, moving along positive x-axis, collides with ball `B`. Just before the collision, speed of ball `'A'` is `4m//s` and ball `'B'` is stantionary. The collision
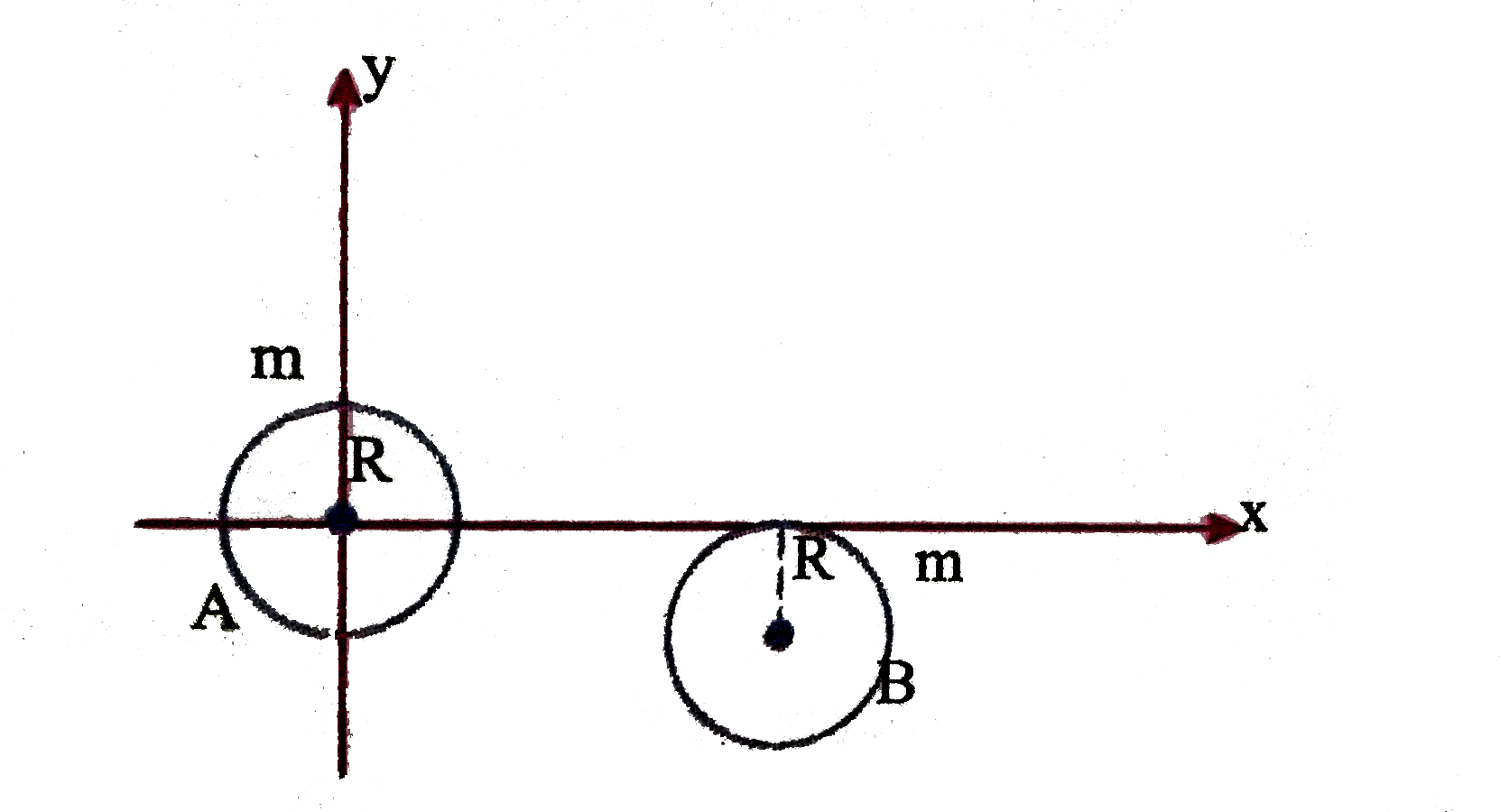
What is velocity of ball `'B'` after collision is
View SolutionTwo smooth balls `A` and `B`, each of mass `m` and radius `R`, have their centres as shown in fig. Ball `A`, moving along positive x-axis, collides with ball `B`. Just before the collision, speed of ball `'A'` is `4m//s` and ball `'B'` is stantionary. The collision
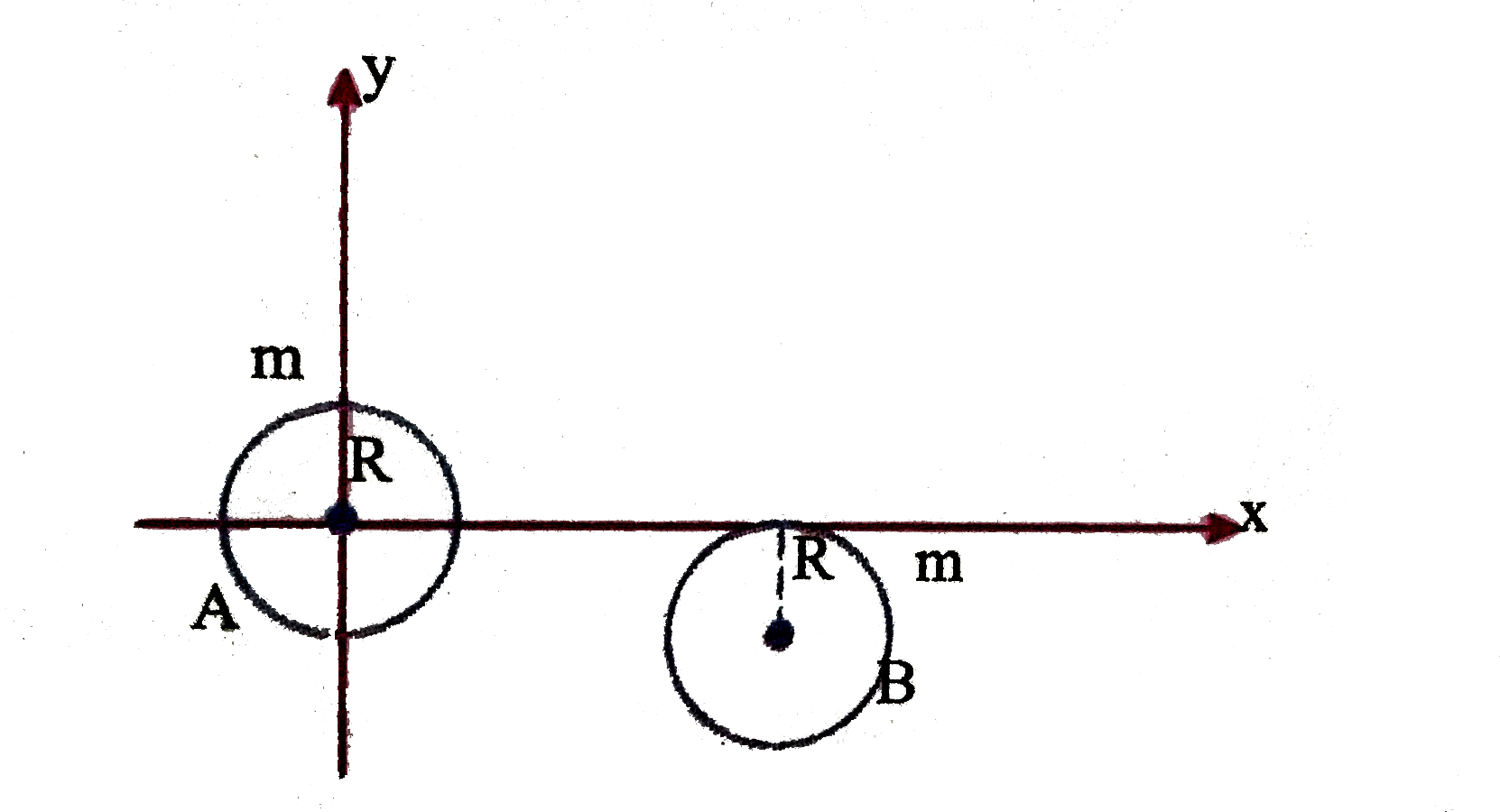
Impluse of the force exerted by `'A'` on `'B'` during the collision is equal to
View SolutionTwo smooth balls `A` and `B`, each of mass `m` and radius `R`, have their centres as shown in fig. Ball `A`, moving along positive x-axis, collides with ball `B`. Just before the collision, speed of ball `'A'` is `4m//s` and ball `'B'` is stantionary. The collision
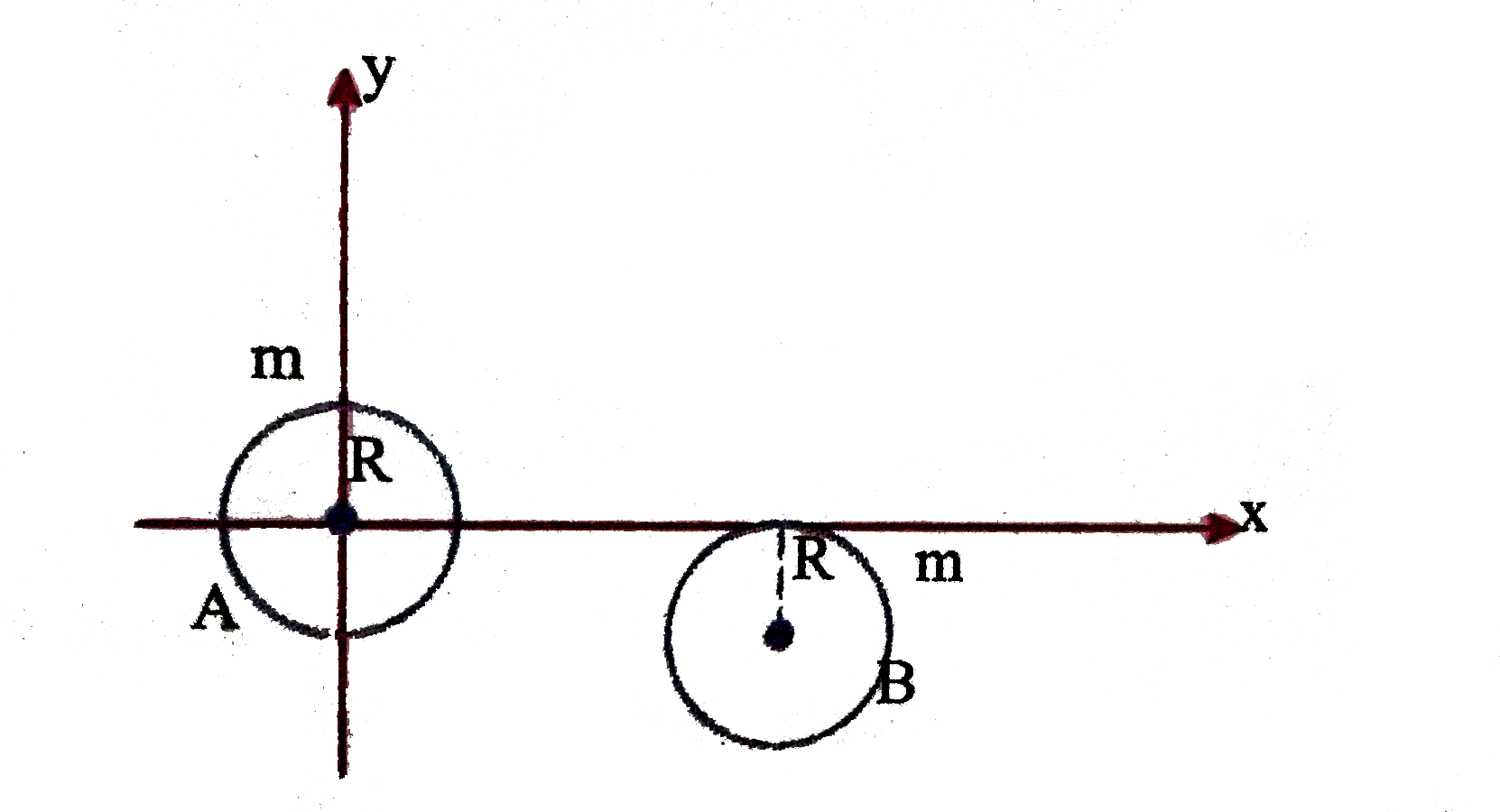
Coefficient of restitution during the collision is changed to `(1)/(2)`, keeping all other parameters unchanged. What is the velocity of the ball `'B'` after the collision.
View SolutionA ball of mass `m` is projected with a velocity `'u'` at angle `theta` with the horizontal. It collides with a smooth box of mass `'M'` at its highest position. If the co-efficient of restitution is `'e'`.
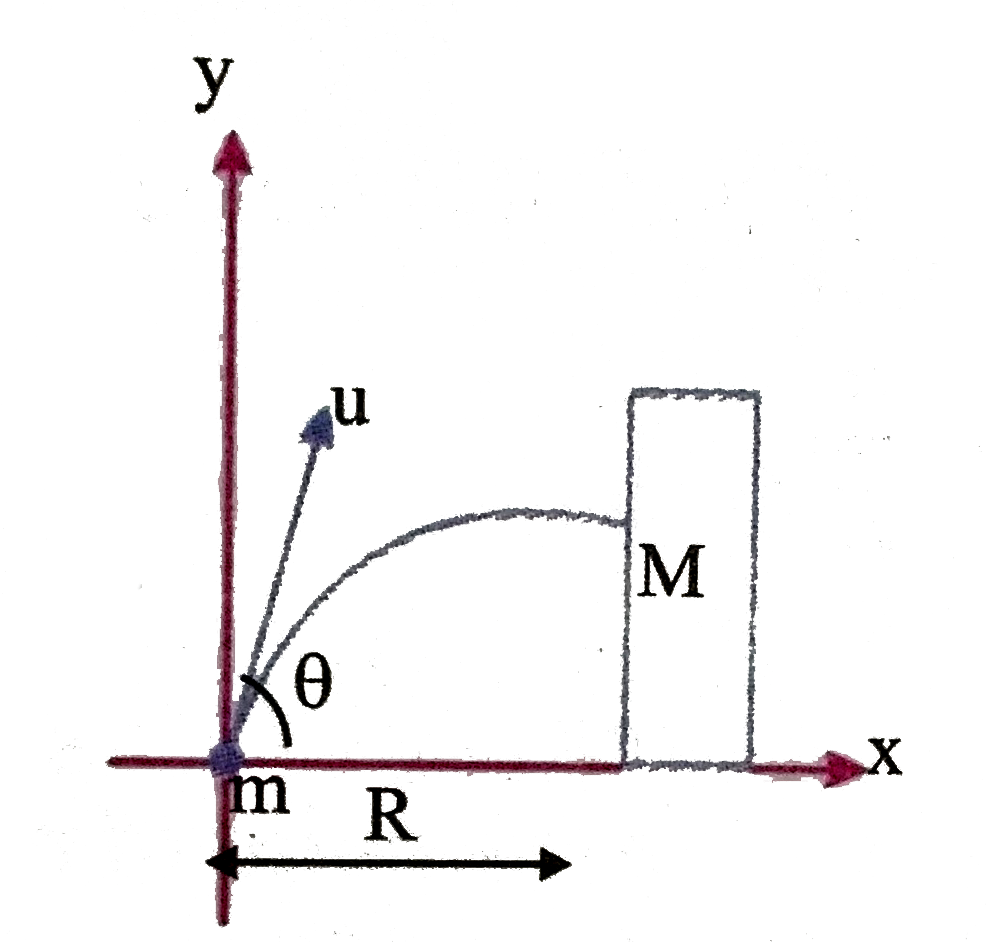
FInd the velocity of the ball after collision
View SolutionA ball of mass `m` is projected with a velocity `'u'` at angle `theta` with the horizontal. It collides with a smooth box of mass `'M'` at its highest position. If the co-efficient of restitution is `'e'`.
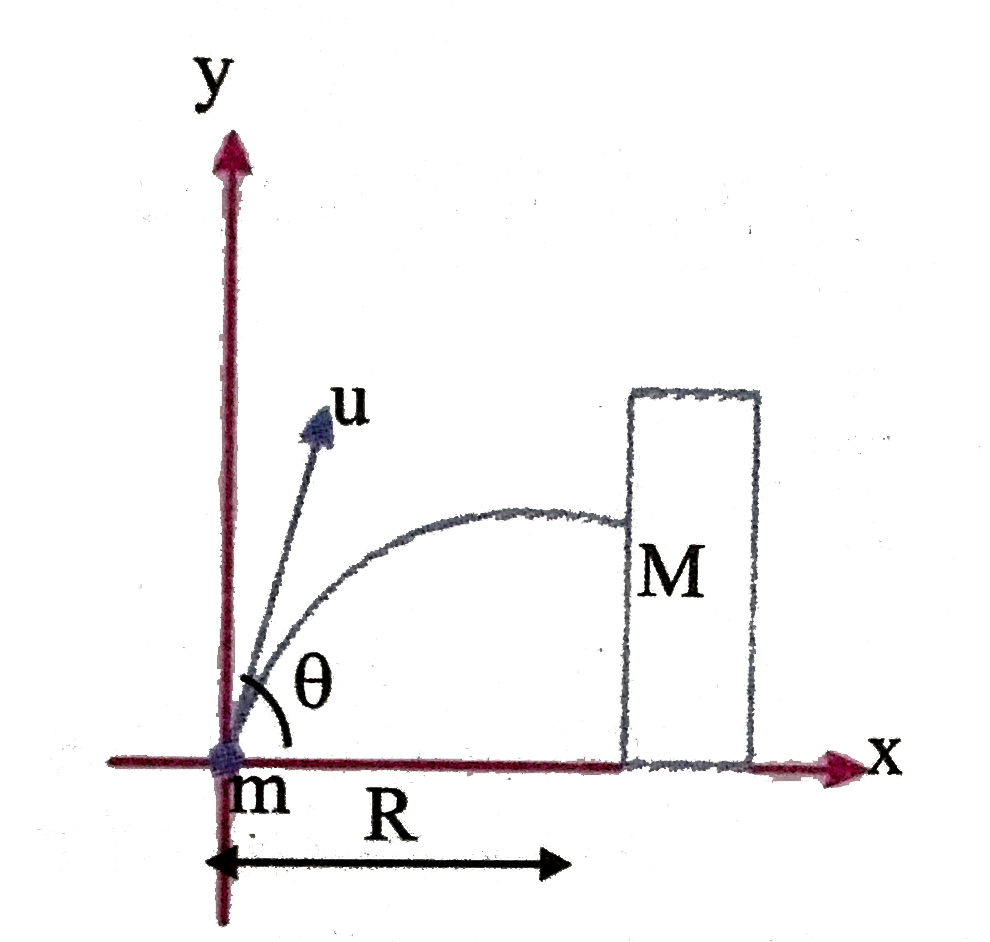
Find the horizontal distance travelled by the ball before collision.
View SolutionA ball of mass `m` is projected with a velocity `'u'` at angle `theta` with the horizontal. It collides with a smooth box of mass `'M'` at its highest position. If the co-efficient of restitution is `'e'`.
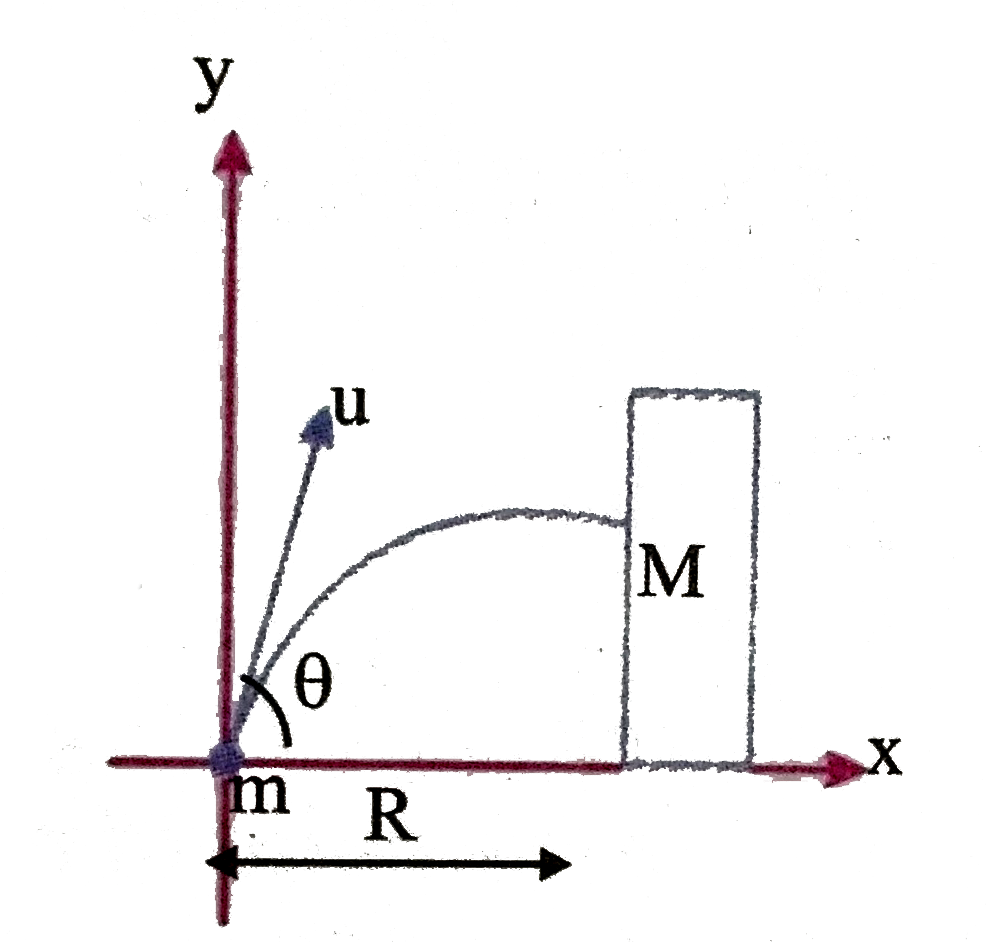
Find the position at which the ball meets the x-axis from the origin
View SolutionAn inelastic ball is projetced with a velocity `'u'` at an angle `'alpha'` to the horizontal, towards a wall distant `'d'` from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is `'e'`)
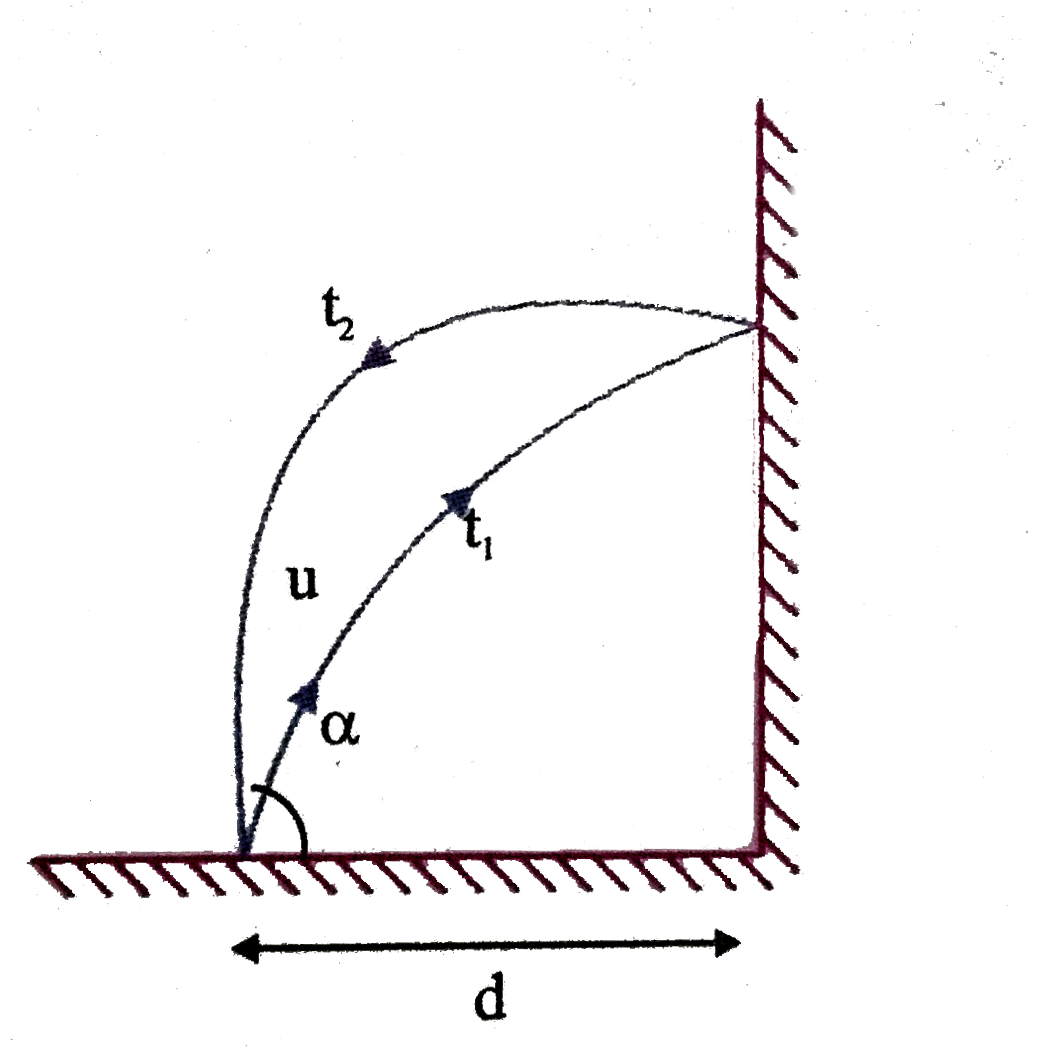
The total time of journey of the ball is
View SolutionAn inelastic ball is projetced with a velocity `'u'` at an angle `'alpha'` to the horizontal, towards a wall distant `'d'` from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is `'e'`)
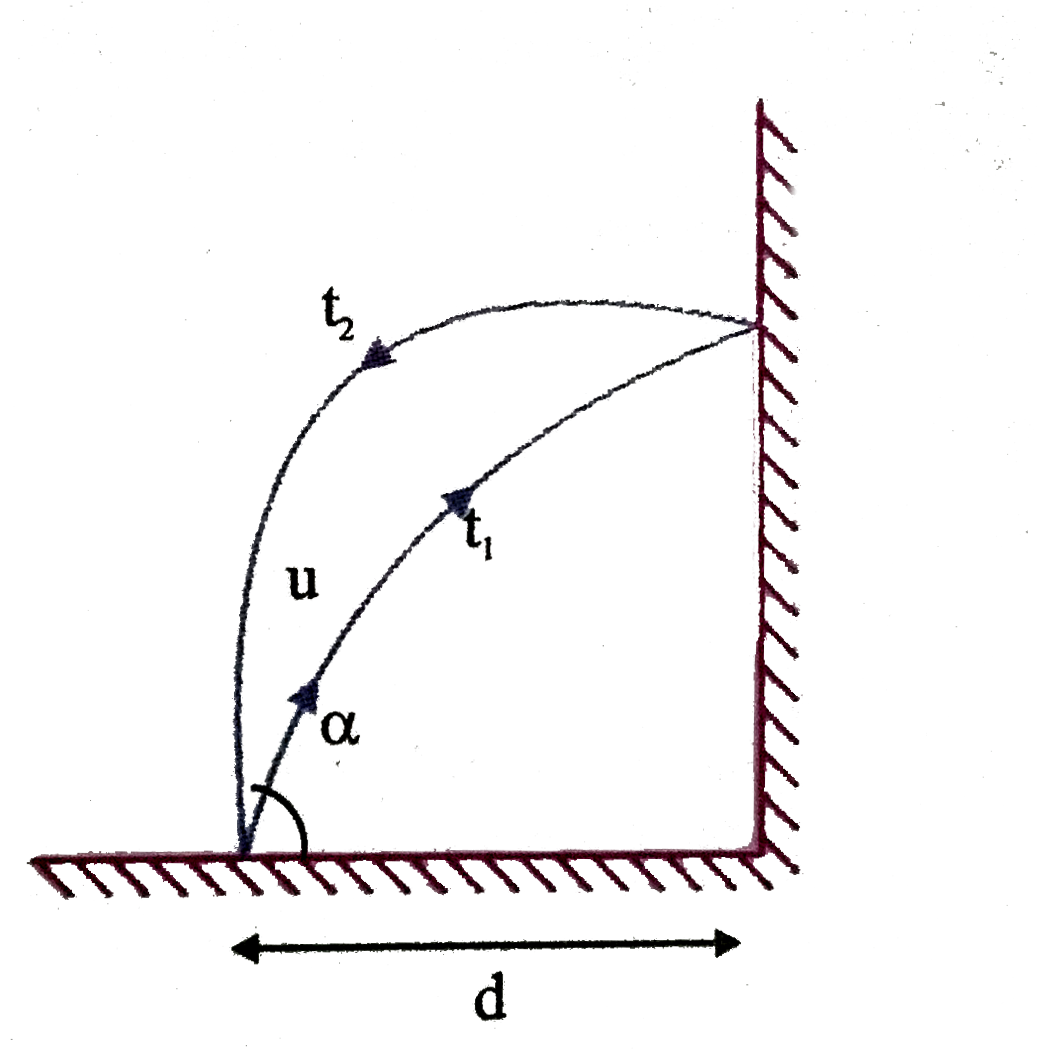
The horizontal distance `'d'` from the wall is
View SolutionAn inelastic ball is projetced with a velocity `'u'` at an angle `'alpha'` to the horizontal, towards a wall distant `'d'` from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is `'e'`)
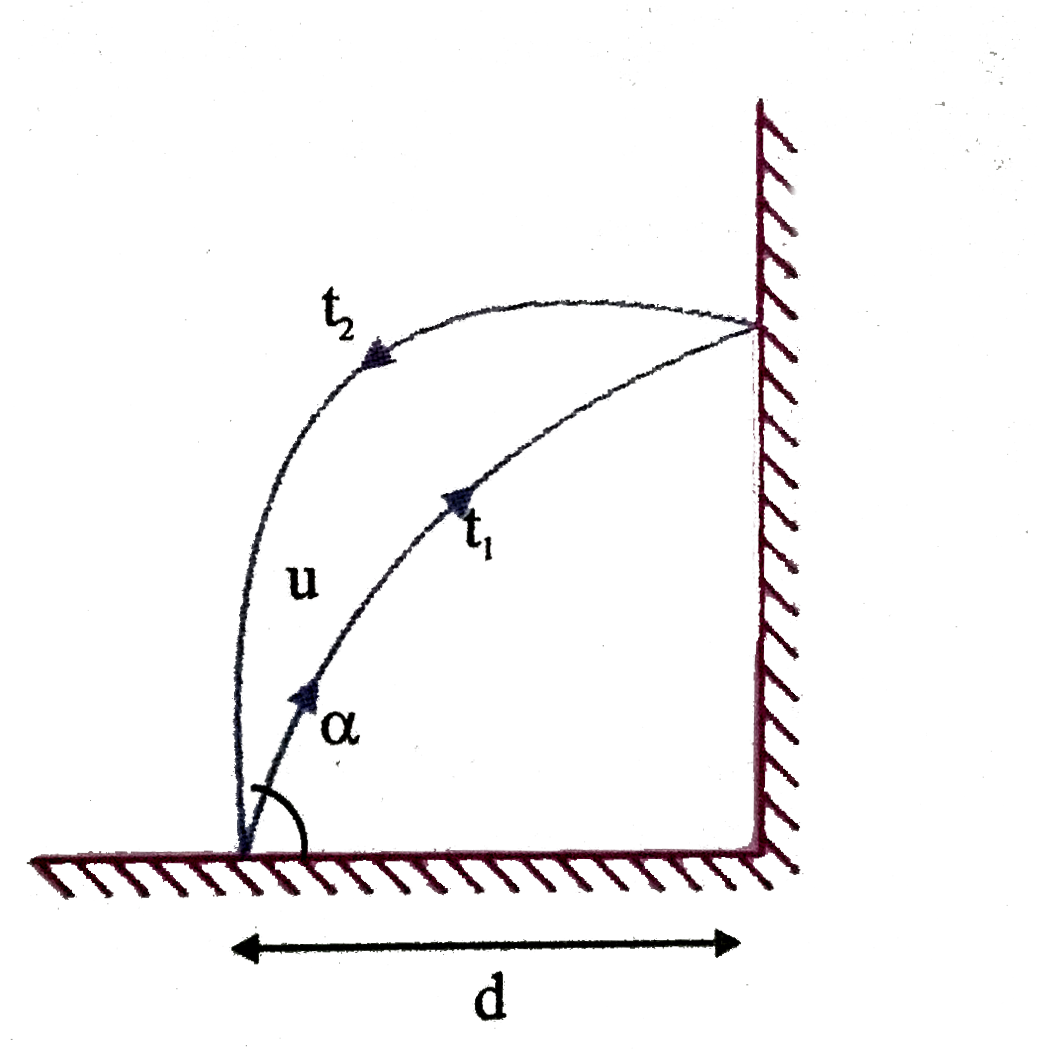
If the line joining the point of projection and the point of impact makes an angle `'theta'` with the horizontal, then `tan theta` is
View SolutionA ball of mass `m = 1 kg` is hung vertically by a thread of length `1=1.50 m`. Upper end of the thread is attached to the ceiling of a trolley of mass `M = 4kg`. Initially, the trolley is stationary and it is free to move along horizontal rails with out friction. A shell of mass `m=1 kg`, moving horizontally with velocity `v_(0) = 6m//s` collides with thread starts to deflect towards right

The velocity of the combined body just after collision is
View SolutionA ball of mass `m = 1 kg` is hung vertically by a thread of length `1=1.50 m`. Upper end of the thread is attached to the ceiling of a trolley of mass `M = 4kg`. Initially, the trolley is stationary and it is free to move along horizontal rails with out friction. A shell of mass `m=1 kg`, moving horizontally with velocity `v_(0) = 6m//s` collides with thread starts to deflect towards right

At the time a maximum deflection of the thread with vertical, the trolley will move with velocity
View SolutionA ball of mass `m = 1 kg` is hung vertically by a thread of length `1=1.50 m`. Upper end of the thread is attached to the ceiling of a trolley of mass `M = 4kg`. Initially, the trolley is stationary and it is free to move along horizontal rails with out friction. A shell of mass `m=1 kg`, moving horizontally with velocity `v_(0) = 6m//s` collides with thread starts to deflect towards right

The maximum deflection of the thread with the vertical is
View SolutionA bullet of mass `'m'` is fired from a gum of mass `M` with a (muzzle) velocity `u`. If the cart on which gun is fixed can move on the smooth horizontal floor as shown

Find recoil velocity of the cart
View SolutionA bullet of mass `'m'` is fired from a gum of mass `M` with a (muzzle) velocity `u`. If the cart on which gun is fixed can move on the smooth horizontal floor as shown

Find maximum compression of spring of spring constant `(K)` is
View SolutionA bullet of mass `'m'` is fired from a gum of mass `M` with a (muzzle) velocity `u`. If the cart on which gun is fixed can move on the smooth horizontal floor as shown

Energy of explosion (or) change in kinetic energy of the system is
View Solution
Comprehension type questions and complete solutions for chapter COLLISION of NARAYANA PHYSICS (HINGLISH) of Class 11