Complete Solutions to Level 2 of chapter THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | THERMODYNAMICS |
| NARENDRA AWASTHI | Level 2 |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
A heating coil is immersed in a 100 g sample of `H_(2)O` (l) at a 1 atm and `100^(@)` C in a closed vessel. In this heating process , `60%` of the liquid is converted to the gaseous form at constant pressure of 1 atm . The densities of liquid and gas under these conditions are 1000 `kg//m^(3)` and 0.60 `kg//m^(3)` respectively . Magnitude of the work done for the process is :
(Take : 1L-atm= 100 J)`
View SolutionA rigid and insulated tank of `3m^(3)` volume is divided into two compartments. One compartment of volume of `2m^(3)` contains an ideal gas at `0.8314` Mpa and 400 K while the second compartment of volume of `1m^(3)` contains the same gas at `8.314` Mpa and 500 K. If the partition between the two compartments is rptured, the final temperature of the gas is :
View SolutionWhat is the value of change in internal energy at 1 atm in the process?
`H_(2)O(l,323K)rarrH_(2)O(g,423K)`
Given : `C_(v,m)(H_(2)O,l)=75.0JK^(-1) mol^(-1):" "C_(p,m)(H_(2)O,g)=33.314JK^(-1)mol^(-1)`
`DeltaH_(vap)"ar 373 K"=40.7KJ//mol`
(a)`42.91kJ//mol`
(b)`43086kJ//mol`
(c)`42.6kJ//mol`
(d)`49.6kJ//mol`
View SolutionFor an ideal gas `(C_(p,m))/(C_(v,m))=gamma`. The molecular mass of the gas is M, its specific heat capacity at constant volume is :
View Solution1 mole of an ideal gas `A(C_(v.m)=3R)` and 2 mole of an ideal gas B are `(C_(v,m)=(3)/(2)R)` taken in a container and expanded reversible and adiabatically from 1 litre of 4 litre starting from initial temperature of 320 K. `DeltaE ` or `DeltaU` for the process is :
View SolutionCalculate the work done by the system in an irreversible (single step) adiabatic expansion of 2 mole of a polyatomic gas `(gamma=4//3)` from 300 K and pressure 10 atm to 1 atm :
View SolutionOne mole of an ideal gas is carried through the reversible cyclic process as shown in figure. The max. temperature attained by the gas duing the cycle
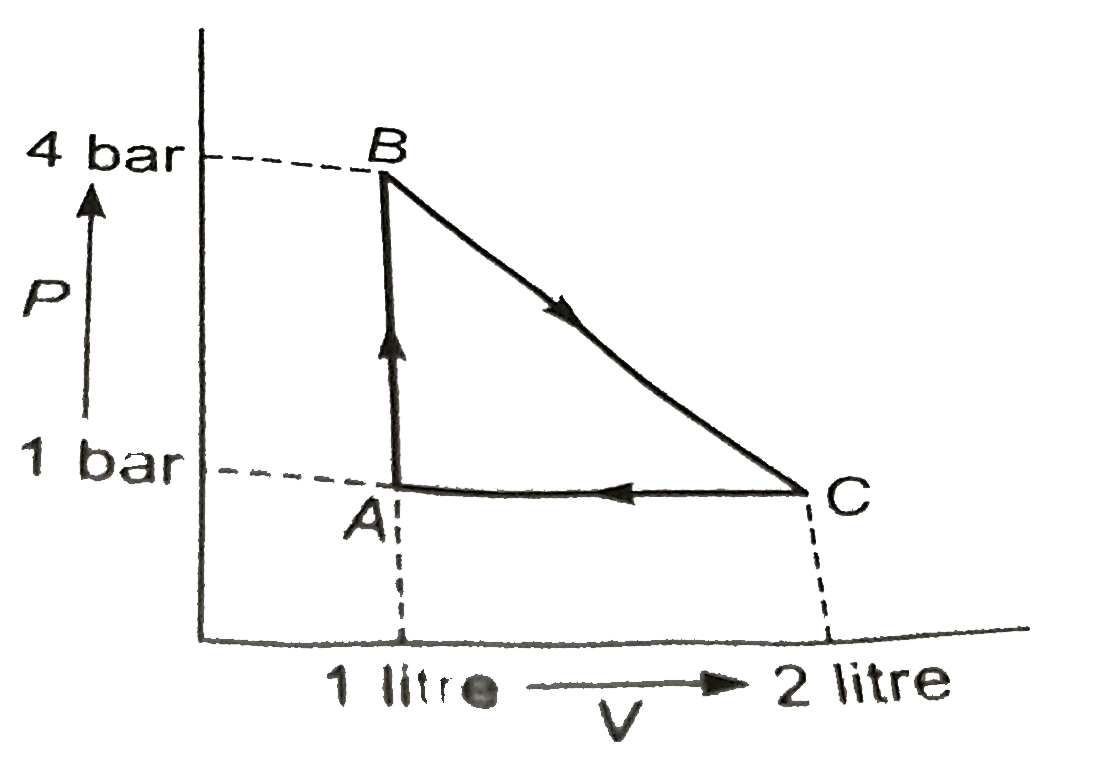
View SolutionTwo moles of a triatomic linear gas (neglect vibration degree of freedom) are taken through a reversible process ideal starting from A as shown in figure.
The volume ratio `(V_(B))/(V_(A))=4`. If the temperature at A is `-73^(@)C`, then :
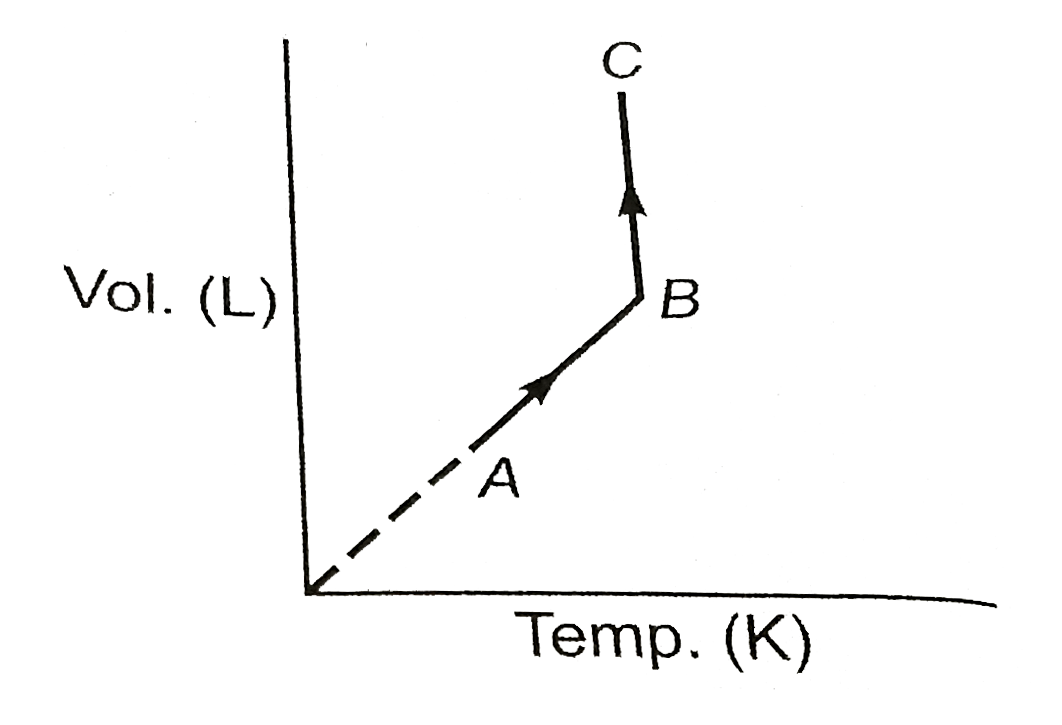
Total enthalpy change in both steps is :
a.3000 R
b.4200 R
c.2100 R
d.0
View SolutionA gas `(C_(v.m) = (5)/(2)R)` behaving ideally is allowed to expand reversibly and adiabatically from `1` litre to `32` litre. Its initial temperature is `327^(@)C`. The molar enthalpy change (in `J//mol`) for the process is :
View SolutionTwo mole of an ideal gas is heated at constant pressure of one atmosphere from `27^(@)C` to `127^(@)C`. If `C_(v,m)=20+10^(-2)"T JK"^(-1).mol^(-1)`, then q and `DeltaU` for the process are respectively:
View Solution10 mole of an ideal gas is heated at constant pressure of one atmosphere from `27^(@)C` to `127^(@)C`. If `C_(v,m)=21.686+10^(-3)T(JK^(-1).mol^(-1))`, then `DeltaH` for the process is :
View SolutionFor polytropic process `PV^(n)` = constant, molar heat capacity `(C_(m))` of an ideal gas is given by:
View Solution2 mole of an ideal monoatomic gas undergoes a reversible process for which `PV^(2)=C`. The gas is expanded from initial volume of 1 L to final volume of 3 L starting from initial temperature of 300 K. Find `DeltaH` for the process :
View SolutionCalculate `DeltaS` for 3 mole of a diatomic ideal gas which is heated and compressed from 298 K and 1 bar to 596 K and 4 bar: [Given: `C_(v,m)(gas)=(5)/(2)R,"ln"(2)=0.70,R=2"cal K^(-1)mol^(-1)`]
View SolutionOne mole of an ideal monoatomic gas at `27^(@)C` is subjected to a reversible isoentropic compression until the temperature reached to `327^(@)C`. If the initial pressure was `1.0 atm`, then find the value of ln `P_(2)`
`(` Given `: ln 2=0.7)`
View SolutionTwo moles of an ideal gas is expanded irreversibly and isothermally at `37^(@)C` until its volume is doubled and `3.41 KJ` heat is absorbed from surrounding. `DeltaS_("total")("system +surrounding")` is:
View SolutionFor a perfectly crystalline solid `C_(p,m)=aT^(3)+bT`, where a and b are constant. If `C_(p,m)` is `0.40` J/K mol at 10 K and `0.92` J/K mol at 20 K, then molar entropy at 20 K is :
View SolutionWhich of the following statement (s) is correct?
Statement-I: The entropy of isolated system with P-V work only, is always maximized at equillibrium.
Statement-2: It is possible for the entropy of closed system to decrease substantialy in an irreversible process.
Statemet-3: Entropy can be crearted but not destroyed.
Statement-4 `DeltaS_(system)` is zero for reversible process in an isolated system.
View SolutionCombustion of sucrose is used by aerobic organisms for providing energy for the life sustaining process. If all the capturing of energy from the reaction is done through electrical process (non P-V work), then calculate, maximum available energy which can be captured by combustion of 34.2 g of sucrose :
(Given : `DeltaH_("combustion")("sucrose")=-6000kJmol^(-1)`
`DeltaS_("combustion")=180j//K-mol` and bodyntemperature is 300 K)
View SolutionFor the hypothetical reaction
`A_(2)(g)+B_(2)(g) to 2AB_(g)`
`DeltaG_(r)^(@)" and " DeltaS_(r)^(@)" are " 20KJ//moland-20JK^(-1)mol^(-1) "respectively at" 200K`
`Delta_(r)C_(p)" is "20 JK^(-1) " then " DeltaH_(r)^(@) "at" 400K is `
View SolutionCalculate `Delta_(r)G^(@)` for `(NH_(4)Cl,s)` at 310K.
Given :`Delta_(r)H^(@)(NH_(4)Cl,s)` =-314 kj/mol,`Delta_(r)C_(p)=0`
`S_(N_(2)(g))^(@)=192 JK^(-1mol^(-1)),S_(H_(2)(g))^(@)=130.5JK^(-1)mol^(-1),`
`S_(Cl_(2)(g))^(@)=233JK mol^(-1), S_(NH_(4)Cl(s))^(@)=99.5JK^(-1)mol^(-1)`
All given data at 300K
View SolutionUsing listed informations, calculate `Delta_(r)G^(@)` (in kJ/mol) at `27^(@)C`
`Co_(3)O_(4)(s)+4CO(g)rarr3Co(s)+4CO_(2)(g)`
Given : At 300 K `DeltaH_(f)^(@)(kJ//mol)-891,-110.5,0.0,-393.5`
`S^(@)(J//K-mol)102.5, 197.7, 30.0, 213.7`
View SolutionFixed mass of an ideal gas collected in a 24.64 litre sealed rigid vessel at 10 atm is heated from `-73^(@)C` to `27^(@)C` calculate change in gibbs free energy if entropy of gas is a function of temperature as `S=2+10^(-2)T(J//K)(1l atm=0.1kJ)`
(a)`1231.5` J
(b)`1281.5` J
(c)`781.5` J
(d)None
View SolutionThe molar heat capacities at constant pressure (assumed constant with respect to temperature ) of A,B and C are in ratio 3:1.5:2.0. the enthyalpy change for the exothermic reaction `A+ 2B to 3C ` at 300k and 310 K is `Delta H_(300)` and `DeltaH_(310)` respectively then:
View SolutionDetermine `Delta U^(@) ` at 300K for the following reaction using the listed enthalpies of reaction :
`4CO(g)+8H_(2)(g)to3CH_(4)(g)+CO_(2)(g)+2H_(2)O(l)`
`C("graphite")+(1)/(2)O_(2)(g)to CO(g), DeltaH_(1)^(@)=-110.5KJ`
` CO(g)(1)/(2)O_(2)(g)toCO_(2)(g), DeltaH_(2)^(@)=-282.9KJ`
`H_(2)(g)+(1)/(2)O_(2)(g)to H_(2)O(l), DeltaH_(3)^(@)=-285.8KJ`
`C("graphite")+2H_(2)(g)to CH_(4)(g), DeltaH_(4)^(@)=-74.8KJ`
View SolutionCalculate `Delta_(f)H^(@)` (in kJ/mol) for `Cr_(2)O_(3)` from the `Delta_(r)G^(@)` and the `S^(@)` values provided at `27^(@)`
`4Cr(s)+3O_(2)(g)rarr2Cr_(2)O_(3)(s)," "Delta_(r)G^(@)=-2093.4kJ//mol`
`S^(@)("J//K mol") : S^(@)(Cr,s)=24," "S^(@)(O_(2),g)=205," "S^(@)(Cr_(2)O_(3),s)=81`
View SolutionCalculate the heat produced (in kJ) when 224 gm of CaO is completely converted to `CaCO_(3)` by reaction with `CO_(2)` at `27^(@)` in a container of fixed volume.
Given : `DeltaH_(f)^(@)(CaCO_(3),s)=-1207kJ//mol," "DeltaH_(f)^(@)(CaO,s)=-635kJ//mol`
`DeltaH_(f)^(@)(CO_(2),g)=-394kJ//mol,["Use R"=8.3JK^(-1)mol^(-1)]`
View SolutionWhen 1.0 g of oxalic acid `(H_(2)C_(2)O_(4))` is burnt in a bomb calorimeter whose capacity is 8.75 KJ/K, the temperature increases by 0.312K, the enthalpy of combustion of oxalic acid at`27^(@)C` is :
View SolutionEnthalpy of neutralization of `H_(3)PO_(3) "with " NaOH " is" -106.68 "kJ"//"mol"`. If enthalpy of neutralization of HCL with NaOH is -55.84`"kJ"//"mole"`, then calculate enthalpy of ionization of `H_(3)PO_(3)` in to its ions in kJ.
View SolutionThe enthalpy of neutralization of a Weak monoprotic acid (HA) in 1 M solution with a strong base is -55.95 KJ/mol . If the unionized acid required 1.4 KJ/mol heat for it's comptate ionzatation and enthalpy of netralization of the strong monobasic acid with a strong monoacidic base is -57.3 KJ/mol . What is the % ionzation of the weak acid in molar solution ?
View SolutionDetermine C-C and C-H bond enthalpy (in `kJ//mol`)
Given : `Delta_(f)H^(@)(C_(2)H_(6),g)=-85kJ//mol," "Delta_(f)H^(@)(C_(3)H_(8),g)=-104kJ//mol`
`Delta_("sub")H^(@)(C,s)=718kJ//mol," "B.E.(H-H)=436kJ//mol`
View SolutionConsider the following data : `Delta_(f)H^(@)(N_(2)H_(4),l)=50kJ//mol,Delta_(f)H^(@)(NH_(3),g)=-46kJ//mol`
`B.E(N-H)=393" kJ//mol and B.E."(H-H)=436kJ//mol`
`Delta_("vap")H(N_(2)H_(4),l)=18kJ//mol`
The N-N bond energy in `N_(2)H_(4)` is :
View SolutionWhat is the bond enthalpy of `Xe-F` bond ?
`XeF_(4)(g)rarrXe^(+)(g)+F^(-)(g)+F_(2)(g)+F(g)," "Delta_(r)H=292"kcal/mol"`
Given : Ionization energy of `Xe=279"kcal/mol"`
`B.E.(F-F) = 30"kcal/mol"`, Electron affinity of F = 85 kcal/mol
View SolutionIf enthaopy of hydrogenation of `C_(6)H_(6)(l)` into `C_(6)H_(12)(l)` is `-205kJ//mol` and resonance energy of `C_(6)H_(6)(l)` is `-152kJ//mol` then enthaopy of hydrogenation of

Assume `DeltaH_("vap")` of `C_(6)H_(6)(l),C_(6)H_(12)(l)` all equal :
View SolutionThe enthalpy of combustion of propance `(C_(3)H_(8))` gas in temes of given of geven data is , Bond energy (kJ/mol)
`underset(+x_(1))(.^(epsi)C-H)underset(+x_(2))(.^(epsi)O-O)underset(+x_(3))(.^(epsi)C-O)underset(+x_(4))(.^(epsi)O-H)underset(+x_(5))(.^(epsi)C-C)`
[Resonance energy of `CO_(2)` is -z KJ/mol and `DeltaH_("vaporization")[H_(2)O(l)" is y " KJ//mol]`
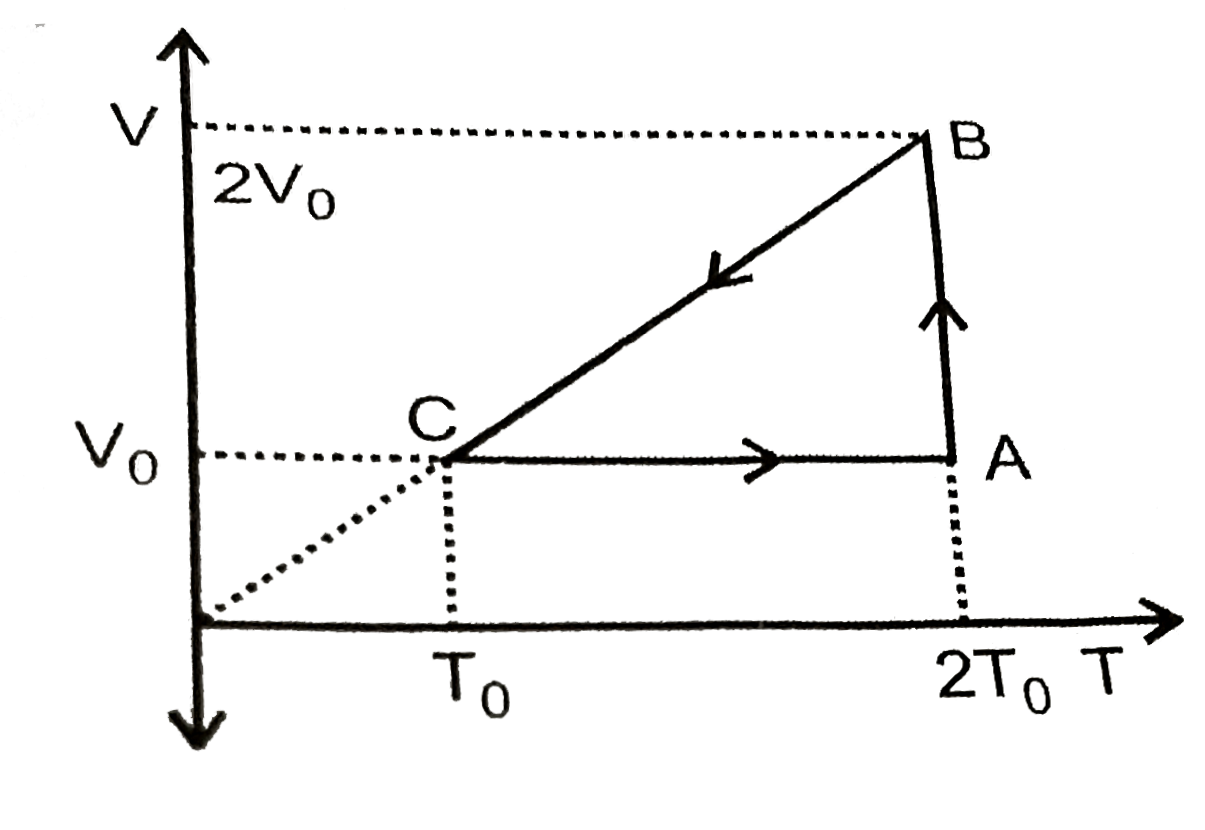
View SolutionThe efficiency of an ideal gas with adiabatic exponent `'gamma'` for the shown cyclic process would be
View SolutionInitially one mole of ideal gas `(C_(v)=(5)/(2)R)` at `0.1` atm and 300 K is put through the following cycle:
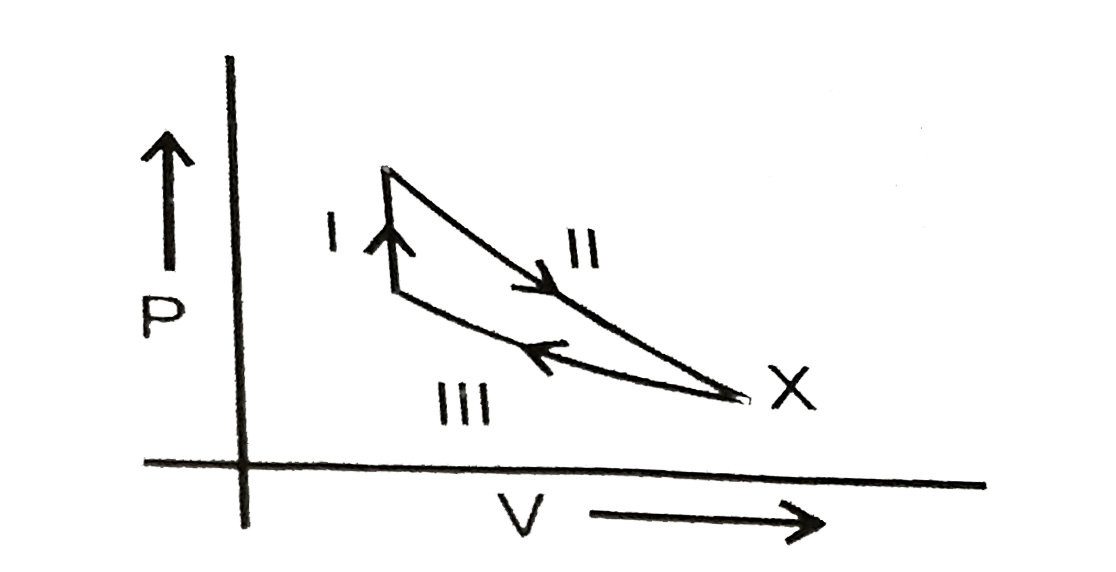
Step-I : Heating to twice its initial pressure at constant volume.
Step-II : Adiabatic expansion to its initial temperature.
Step-III : Isothermal compression back to `1.00` atm.
what is the volume at state X?
View SolutionWhat is the enthalpy of neutralization of HF against a strong base?
Given : `H^(+)(aq)+OH^(-)(aq)rarrH_(2)O(l),Delta_(r)H^(@)=-56kJ//mol`
`Delta_(s)H^(@)(HF,aq)=-329kJ//mol,Delta_(s)H^(@)(H_(2)O,l)=-285kJ//mol`
`Delta_(s)H^(@)(F^(-),aq)=-320 " kJ"//"mol"`
View SolutionThe molar heat capacities of Iodine vapour and solid are `7.8` and 14 cal/mol respectively. If enthalpy of iodine is 6096 cal/mol at `200^(@)C`, then what is `DeltaU` (internal energy change) at `250^(@)C` in cal/mol
View SolutionFor the reaction taking place at certain temperature `NH_(2)COONH_(4)(s)hArr2NH_(3)(g)+CO_(2)(g)` if equilibrium pressure is 3 X bar then `Delta_(r)G^(@)` would be
View Solution
Level 2 questions and complete solutions for chapter THERMODYNAMICS of NARENDER AVASTHI CHEMISTRY (ENGLISH) of Class 11