Complete Solutions to Level 3 of chapter THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | THERMODYNAMICS |
| NARENDRA AWASTHI | Level 3 |
| Number Of Questions | 89 |
| Academic Year | 2023-24 |
The first law of thermodynamics for a closed system is dU = dq + dw, where dw = `dw_(pv)+dw_("non-pv")`. The most common type of `w_("non-pv")` is electrical work. As per IUPAC convention work done on the system is positive.
A system generates 50 J electrical energy, has 150 J of pressure-volume work done on it by the surroundings while releasing 300 J of heat energy. What is the change in the internal energy of the sytem?
View SolutionThe first law of thermodynamics for a closed system is dU = dq + dw, where dw = `dw_(pv)+dw_("non-pv")`. The most common type of `w_("non-pv")` is electrical work. As per IUPAC convention work done on the system is positive.
A system generates 50 J of electrical energy and delivers 150 J of pressure-volume work against the surroundings while releasing 300 J of heat energy. What is the change in the internal energy of the system?
View SolutionIf the boundary of system moves by an infinitesimal amount, the work involved is given by `dw=-P_("ext")dV`
for irreversible process `w=-P_("ext")DeltaV " "( "where "DeltaV=V_(f)-V_(i))`
for reversible process `P_("ext")=P_("int")pmdP~=P_("int")`
so for reversible isothermal process `w = -nRTln.(V_(f))/(V_(i))`
2mole of an ideal gas undergoes isothermal compression along three different plaths :
(i) reversible compression from `P_(i)=2` bar and `V_(i) = 8L` to `P_(f) = 20` bar
(ii) a single stage compression against a constant external pressure of 20 bar, and
(iii) a two stage compression consisting initially of compression against a constant external pressure of 10 bar until `P_("gas")=P_("ext")`, followed by compression against a constant pressure of 20 bar until `P_("gas") = P_("ext")`
Work done (in bar-L) on the gas in reversible isothermal compression is :
View SolutionIf the boundary of system moves by an infinitesimal amount, the work involved is given by `dw=-P_("ext")dV`
for irreversible process `w=-P_("ext")DeltaV " "( "where "DeltaV=V_(f)-V_(i))`
for reversible process `P_("ext")=P_("int")pmdP~=P_("int")`
so for reversible isothermal process `w = -nRTln.(V_(f))/(V_(i))`
2mole of an ideal gas undergoes isothermal compression along three different plaths :
(i) reversible compression from `P_(i)=2` bar and `V_(i) = 8L` to `P_(f) = 20` bar
(ii) a single stage compression against a constant external pressure of 20 bar, and
(iii) a two stage compression consisting initially of compression against a constant external pressure of 10 bar until `P_("gas")=P_("ext")`, followed by compression against a constant pressure of 20 bar until `P_("gas") = P_("ext")`
Work done on the gas in single stage compression is :
View SolutionIf the boundary of system moves by an infinitesimal amount, the work involved is given by `dw=-P_("ext")dV`
for irreversible process `w=-P_("ext")DeltaV " "( "where "DeltaV=V_(f)-V_(i))`
for reversible process `P_("ext")=P_("int")pmdP~=P_("int")`
so for reversible isothermal process `w = -nRTln.(V_(f))/(V_(i))`
2mole of an ideal gas undergoes isothermal compression along three different plaths :
(i) reversible compression from `P_(i)=2` bar and `V_(i) = 8L` to `P_(f) = 20` bar
(ii) a single stage compression against a constant external pressure of 20 bar, and
(iii) a two stage compression consisting initially of compression against a constant external pressure of 10 bar until `P_("gas")=P_("ext")`, followed by compression against a constant pressure of 20 bar until `P_("gas") = P_("ext")`
Total work done on the gas in two stage compression is :
View SolutionIf the boundary of system moves by an infinitesimal amount, the work involved is given by `dw=-P_("ext")dV`
for irreversible process `w=-P_("ext")DeltaV " "( "where "DeltaV=V_(f)-V_(i))`
for reversible process `P_("ext")=P_("int")pmdP~=P_("int")`
so for reversible isothermal process `w = -nRTln.(V_(f))/(V_(i))`
2mole of an ideal gas undergoes isothermal compression along three different paths :
(i) reversible compression from `P_(i)=2` bar and `V_(i) = 8L` to `P_(f) = 20` bar
(ii) a single stage compression against a constant external pressure of 20 bar, and
(iii) a two stage compression consisting initially of compression against a constant external pressure of 10 bar until `P_("gas")=P_("ext")`, followed by compression against a constant pressure of 20 bar until `P_("gas") = P_("ext")`
Order of magnitude of work is :
View SolutionStandard Gibb's energy of reaction `(Delta_(r )G^(@))` at a certain temperature can be computed `Delta_(r )G^(@)=Delta_(r)H^(@)-T.Delta_(r )S^(@)` and the change in the value of `Delta_(r)H^(@)` and `Delta_(r)S^(@)` for a reaction with temperature can be computed as follows :
`Delta_(r )H_(T_(2))^(@)-Delta_(r )H_(T_(1))^(@)=Delta_(r )C_(p)^(@)(T_(2)-T_(1))`
`Delta_(r )S_(T_(2))^(@)-Delta_(r )S_(T_(1))^(@)=Delta_(r )C_(p)^(@)ln.(T_(2)/T_(1))`
`" "Delta_(r )G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)`
and `" by "Delta_(r )G^(@)=-"RT " ln K_(eq)`.
Consider the following reaction : `CO(g)+2H_(2)(g)iffCH_(3)OH(g)`
Given : `Delta_(f)H^(@)(CH_(3)OH,g)=-201 " kJ"//"mol", " "Delta_(f)H^(@)(CO,g)=-114" kJ"//"mol"`
`S^(@)(CH_(3)OH,g)=240" J"//"K-mol, "S^(@)(H_(2),g)=29" JK"^(-1)" mol"^(-1)`
`S^(@)(CO,g)=198 " J"//"mol-K, "C_(p,m)^(@)(H_(2))=28.8 " J"//"mol-K"`
`C_(p,m)^(@)(CO)=29.4 " J"//"mol-K, "C_(p,m)^(@)(CH_(3)OH)=44 " J"//"mol-K"`
and `" "ln ((320)/(300))=0.06`, all data at 300 K
`Delta_(r )S^(@)` at 300 K for the reaction is :
View SolutionStandard Gibb's energy of reaction `(Delta_(r )G^(@))` at a certain temperature can be computed `Delta_(r )G^(@)=Delta_(r)H^(@)-T.Delta_(r )S^(@)` and the change in the value of `Delta_(r)H^(@)` and `Delta_(r)S^(@)` for a reaction with temperature can be computed as follows :
`Delta_(r )H_(T_(2))^(@)-Delta_(r )H_(T_(1))^(@)=Delta_(r )C_(p)^(@)(T_(2)-T_(1))`
`Delta_(r )S_(T_(2))^(@)-Delta_(r )S_(T_(1))^(@)=Delta_(r )C_(p)^(@)ln.(T_(2)/T_(1))`
`" "Delta_(r )G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)`
and `" by "Delta_(r )G^(@)=-"RT " ln K_(eq)`.
Consider the following reaction : `CO(g)+2H_(2)(g)iffCH_(3)OH(g)`
Given : `Delta_(f)H^(@)(CH_(3)OH,g)=-201 " kJ"//"mol", " "Delta_(f)H^(@)(CO,g)=-114" kJ"//"mol"`
`S^(@)(CH_(3)OH,g)=240" J"//"K-mol, "S^(@)(H_(2),g)=29" JK"^(-1)" mol"^(-1)`
`S^(@)(CO,g)=198 " J"//"mol-K, "C_(p,m)^(@)(H_(2))=28.8 " J"//"mol-K"`
`C_(p,m)^(@)(CO)=29.4 " J"//"mol-K, "C_(p,m)^(@)(CH_(3)OH)=44 " J"//"mol-K"`
and `" "ln ((320)/(300))=0.06`, all data at 300 K
`Delta_(r )H^(@)` at 300 K for the reaction is :
View SolutionStandard Gibb's energy of reaction `(Delta_(r )G^(@))` at a certain temperature can be computed `Delta_(r )G^(@)=Delta_(r)H^(@)-T.Delta_(r )S^(@)` and the change in the value of `Delta_(r)H^(@)` and `Delta_(r)S^(@)` for a reaction with temperature can be computed as follows :
`Delta_(r )H_(T_(2))^(@)-Delta_(r )H_(T_(1))^(@)=Delta_(r )C_(p)^(@)(T_(2)-T_(1))`
`Delta_(r )S_(T_(2))^(@)-Delta_(r )S_(T_(1))^(@)=Delta_(r )C_(p)^(@)ln.(T_(2)/T_(1))`
`" "Delta_(r )G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)`
and `" by "Delta_(r )G^(@)=-"RT " ln K_(eq)`.
Consider the following reaction : `CO(g)+2H_(2)(g)iffCH_(3)OH(g)`
Given : `Delta_(f)H^(@)(CH_(3)OH,g)=-201 " kJ"//"mol", " "Delta_(f)H^(@)(CO,g)=-114" kJ"//"mol"`
`S^(@)(CH_(3)OH,g)=240" J"//"K-mol, "S^(@)(H_(2),g)=29" JK"^(-1)" mol"^(-1)`
`S^(@)(CO,g)=198 " J"//"mol-K, "C_(p,m)^(@)(H_(2))=28.8 " J"//"mol-K"`
`C_(p,m)^(@)(CO)=29.4 " J"//"mol-K, "C_(p,m)^(@)(CH_(3)OH)=44 " J"//"mol-K"`
and `" "ln ((320)/(300))=0.06`, all data at 300 K
`Delta_(r )S^(@)` at 320 K is :
View SolutionStandard Gibb's energy of reaction `(Delta_(r )G^(@))` at a certain temperature can be computed `Delta_(r )G^(@)=Delta_(r)H^(@)-T.Delta_(r )S^(@)` and the change in the value of `Delta_(r)H^(@)` and `Delta_(r)S^(@)` for a reaction with temperature can be computed as follows :
`Delta_(r )H_(T_(2))^(@)-Delta_(r )H_(T_(1))^(@)=Delta_(r )C_(p)^(@)(T_(2)-T_(1))`
`Delta_(r )S_(T_(2))^(@)-Delta_(r )S_(T_(1))^(@)=Delta_(r )C_(p)^(@)ln.(T_(2)/T_(1))`
`" "Delta_(r )G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)`
and `" by "Delta_(r )G^(@)=-"RT " ln K_(eq)`.
Consider the following reaction : `CO(g)+2H_(2)(g)iffCH_(3)OH(g)`
Given : `Delta_(f)H^(@)(CH_(3)OH,g)=-201 " kJ"//"mol", " "Delta_(f)H^(@)(CO,g)=-114" kJ"//"mol"`
`S^(@)(CH_(3)OH,g)=240" J"//"K-mol, "S^(@)(H_(2),g)=29" JK"^(-1)" mol"^(-1)`
`S^(@)(CO,g)=198 " J"//"mol-K, "C_(p,m)^(@)(H_(2))=28.8 " J"//"mol-K"`
`C_(p,m)^(@)(CO)=29.4 " J"//"mol-K, "C_(p,m)^(@)(CH_(3)OH)=44 " J"//"mol-K"`
and `" "ln ((320)/(300))=0.06`, all data at 300 K
`Delta_(r )H^(@)` at 320 K is :
View SolutionConsider the following reaction : `CO(g)+2H_(2)(g)iffCH_(3)OH(g)`
Given : `Delta_(f)H^(@)(CH_(3)OH,g)=-201 " kJ"//"mol", " "Delta_(f)H^(@)(CO,g)=-114" kJ"//"mol"`
`S^(@)(CH_(3)OH,g)=240" J"//"K-mol, "S^(@)(H_(2),g)=29" JK"^(-1)" mol"^(-1)`
`S^(@)(CO,g)=198 " J"//"mol-K, "C_(p,m)^(@)(H_(2))=28.8 " J"//"mol-K"`
`C_(p,m)^(@)(CO)=29.4 " J"//"mol-K, "C_(p,m)^(@)(CH_(3)OH)=44 " J"//"mol-K"`
and `" "ln ((320)/(300))=0.06`, all data at 300 K
`Delta_(r )G^(@)` at 320 K is :
View SolutionEnthalpy of neutralization is defined as the enthalpy change when 1 mole of acid`/ /`base is completely neutralized by base `//`acid in dilute solution .
For Strong acid and strong base neutralization net chemical change is
`H^(+) (aq)+OH^(-)(aq)to H_(2)O(l)`
`Delta_(r)H^(@)=-55.84KJ//mol`
`DeltaH_("ionization")^(@)` of aqueous solution of strong acid and strong base is zero .
when a dilute solution of weak acid or base is neutralized, the enthalpy of neutralization is somewhat less because of the absorption of heat in the ionzation of the because of the absorotion of heat in the ionization of the weak acid or base ,for weak acid /base
`DeltaH_("neutrlzation")^(@)=DeltaH_("ionization")^(@)+ Delta _(r)H^(@)(H^(+)+OH^(-)to H_(2)O)`
If enthalpy of neutralization of `CH_(3)COOH` by NaOH is -49.86KJ`//`mol then enthalpy of ionization of `CH_(3)COOH` is:
(a)5.98 kJ/mol
(b)`-5.98` kJ/mol
(c)105.7 kJ/mol
(d)None of these
View SolutionEnthalpy of neutralzation is defined as the enthalpy change when 1 mole of acid /base is completely neutralized by base `//`acid in dilute solution .
For Strong acid and strong base neutralization net chemical change is
`H^(+) (aq)+OH^(-)(aq)to H_(2)O(l)`
`Delta_(r)H^(@)=-55.84KJ//mol`
`DeltaH_("ionization")^(@)` of aqueous solution of strong acid and strong base is zero .
when a dilute solution of weak acid or base is neutralized, the enthalpy of neutralization is somewhat less because of the absorption of heat in the ionzation of the because of the absorotion of heat in the ionization of the weak acid or base ,for weak acid /base
`DeltaH_("neutrlzation")^(@)=DeltaH_("ionization")^(@)+ Delta _(r)H^(@)(H^(+)+OH^(-)to H_(2)O)`
What is `DeltaH^(@)` for complate neutralization of strong diacidic base `A(OH)_(2)by HNO_(3)`?
View SolutionEnthalpy of neutralzation is defined as the enthalpy change when 1 mole of acid `//`base is completely neutralized by base `//`acid in dilute solution .
For Strong acid and strong base neutralization net chemical change is
`H^(+) (aq)+OH^(-)(aq)to H_(2)O(l)`
`Delta_(r)H^(@)=-55.84KJ//mol`
`DeltaH_("ionization")^(@)` of aqueous solution of strong acid and strong base is zero .
when a dilute solution of weak acid or base is neutralized, the enthalpy of neutralization is somewhat less because of the absorption of heat in the ionzation of the because of the absorotion of heat in the ionization of the weak acid or base ,for weak acid /base
`DeltaH_("neutrlzation")^(@)=DeltaH_("ionization")^(@)+ Delta _(r)H^(@)(H^(+)+OH^(-)to H_(2)O)`
under same conditions ,how many mL of 0.1 m NaOH and 0.05 M `H_(2)A` (strong diprotic acid ) solution should be mixed for a total volume of 100mL to producce the hight rise in temperature ?
View SolutionGibbs Helmholtz equation relates the enthalpy, entropy and free energy change of the process at constant pressure and temperature as
`DeltaG=DeltaH-TDeltaS " (at constant P, T)"`
In General the magnitude of `DeltaH` does not change much with the change in temperature but the terms `TDeltaS` changes appreciably. Hence in some process spontaneity is very much dependent on temperature and such processes are generally known as entropy driven process.
Fro the reaction at 298 K, `A_(2)B_(4)rarr2AB_(2)`
`DeltaH=2" kJ"` and `DeltaS` = 20 J/K at constant P and T, the reaction will be
View SolutionGibbs Helmholtz equation relates the enthalpy, entropy and free energy change of the process at constant pressure and temperature as
`DeltaG=DeltaH-TDeltaS " (at constant P, T)"`
In General the magnitude of `DeltaH` does not change much with the change in temperature but the terms `TDeltaS` changes appreciably. Hence in some process spontaneity is very much dependent on temperature and such processes are generally known as entropy driven process.
When `CaCO_(3)` is heated to a high temperature it decomposes into CaO and `CO_(2)`, however it is quite stable at room temperature. It can be explained by the fact that
View SolutionGibbs Helmholtz equation relates the enthalpy, entropy and free energy change of the process at constant pressure and temperature as
`DeltaG=DeltaH-TDeltaS " (at constant P, T)"`
In General the magnitude of `DeltaH` does not change much with the change in temperature but the terms `TDeltaS` changes appreciably. Hence in some process spontaneity is very much dependent on temperature and such processes are generally known as entropy driven process.
The Dissolution of `CaCl_(2).6H_(2)O` in a large volume of water is endothermic to the extent of 3.5 kcal `"mol"^(-1)` and `DeltaH` for the reaction is -23.2 kcal `"mol"^(-1)`.
`CaCl_(2)(s)+6H_(2)O(l)rarrCaCl_(2).6H_(2)O(s)`
Select the correct statement :
View SolutionIdentify the intensive quantities from the following :
(a)Enthalpy
(b)Temperature
(c)Pressure
(d)Mass
View SolutionIdentify the extensive quantities from the following :
View SolutionIdentify the state functions from the following :
View SolutionWhich of the following statementl is/are correct as per IUPAC sign convention?
View SolutionIn an isothermal irreversible expansion of an ideal gas as per IUPAC sign convention :
View SolutionIn reversible isothermal expansion of an ideal gas :
View SolutionAn adiabatic process is that process in which :
a.energy is transferred as heat
b.no energy is transferred as heat
c.`DeltaU = w`
d.the temp. of gas increases in a reversible compression
View SolutionIn adiabatic process, the work involved during expansion or compression of an ideal gas is given by :
View Solution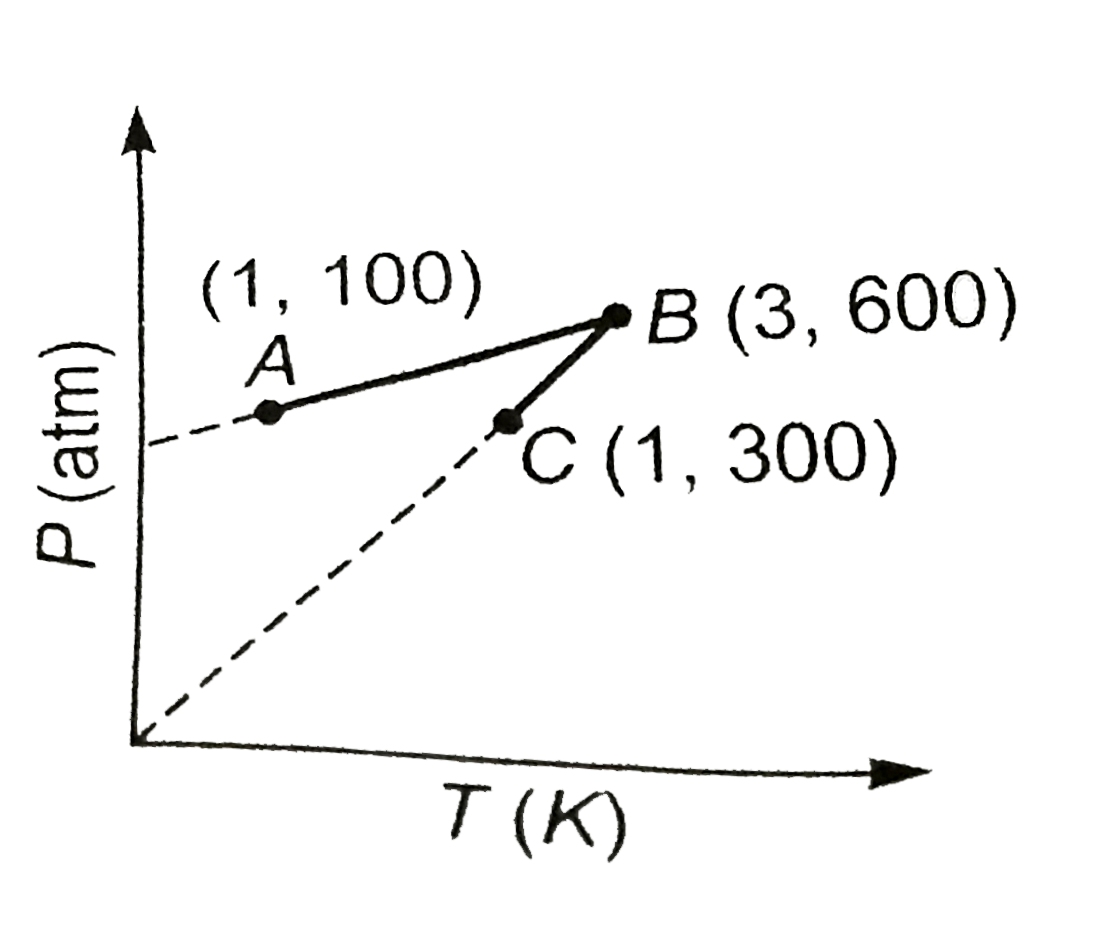
One mole of an ideal gas is subjected to a two step reversible process (A-B and B-C). The pressure at A and C is same. Mark the correct statement(s) :
View SolutionAssume ideal gas behaviour for all the gases considered and neglect vibrational degrees of freedom. Separate equimolar sample. Separate equimolar samples of Ne, `O_(2)` , `CO_(2)` and `SO_(2)` were subjected to a two process as mentioned. Initially all are at same state of temperature and pressue.
Step I `rarr` All undergo reversible adiabatic expansion to attain same final volume, which is double the original volume thereby causing the decreases in their temperature.
Step II `rarr` After step I all are given appropriate amount of heat isochorically to restore the original temperature.
Mark the correct option(s) :
View SolutionWhich of the following is/are correct?
View Solution`DeltaHltDeltaU` for the reaction(s) :
View SolutionWhich of the following conditions may lead to a non-spontaneous change?
a.`DeltaH " and "DeltaS " both "+ve`
b.`DeltaH=-ve,DeltaS=+ve`
c.`DeltaH=+ve,DeltaS=-ve`
d.`DeltaH=-ve,DeltaS=-ve`
View SolutionFor a process to be spontaneous :
View SolutionThe normal boiling point of a liquid X is 400 K. Which of the following statement is true about the process `X(l) to X(g)` ?
View SolutionWhen ice melts at `1^(@)C` :
(a)an increase in entropy
(b)a decrease in enthalpy
(c)a decrease in free energy
(d)process is spontaneous
View SolutionThe value of `DeltaH_("transition")` of C (graphite) `rarr` C (diamond) is 1.9 kJ/mol at `25^(@)C`. Entropy of graphite is higher than entropy of diamond. This implies that :
View SolutionWhich of the following statement(s) is/are false?
View SolutionWhich of the following statement(s) is/are true?
View SolutionFrom the following date , mark the opation(s) where `Delta H` is correctly written for the given reaction .
Given: `H+(aq) +OH-(aq) to H_(2)O(l),`
`DeltaH=-57.3 kJ`
`DeltaH_(solution) HA(g)=-70.7 kJ"mole"`
`DeltaH_(solution) BOH(g)=- 20 kJ"mole"`
`DeltaH_("ionzatoin") ` of `HA=15 kJ//"mole"` and BOH is a strong base.

View SolutionSelect correct statement(s)
View SolutionFor an isolated system, the entropy :
View SolutionThe normal boiling point of a liquid X is 400 K. `DeltaH_("vap")` at normal boiling point is 40 kJ/mol. Select correct statement(s) :
View SolutionSelect incorrect statement(s)
View SolutionSelect correct statement(s) for the reaction `H_(2)O(g)+CO(g)rarrH_(2)(g)+CO_(2)(g)` substance
`CO(g)" "CO_(2)(g)" "H_(2)O(g)" "H_(2)(g)`
`Delta_(f)H_(400)^(@)("kcal mol"^(-1))" -25 -95 -55 0"`
`S_(400)^(@)("cal mol"^(-1)"K"^(-1)) " 45 50 40 30"`
View SolutionMatch the following columns
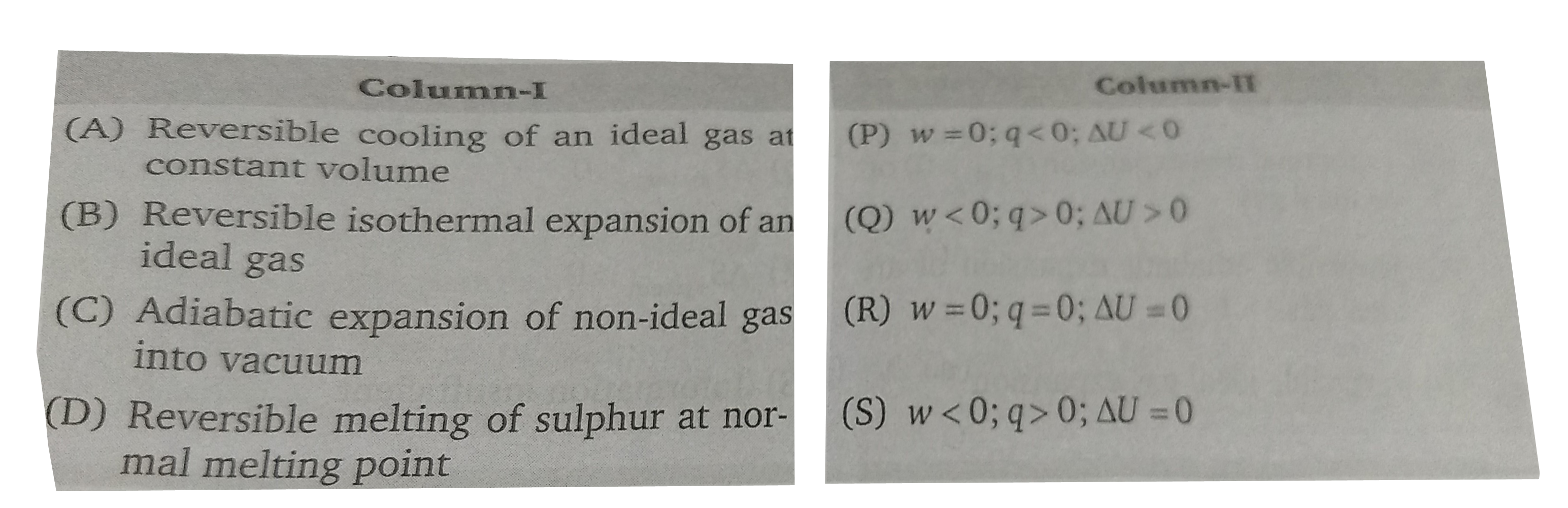
View SolutionMatch the following columns

View SolutionMatch the following Column - I and Column - II
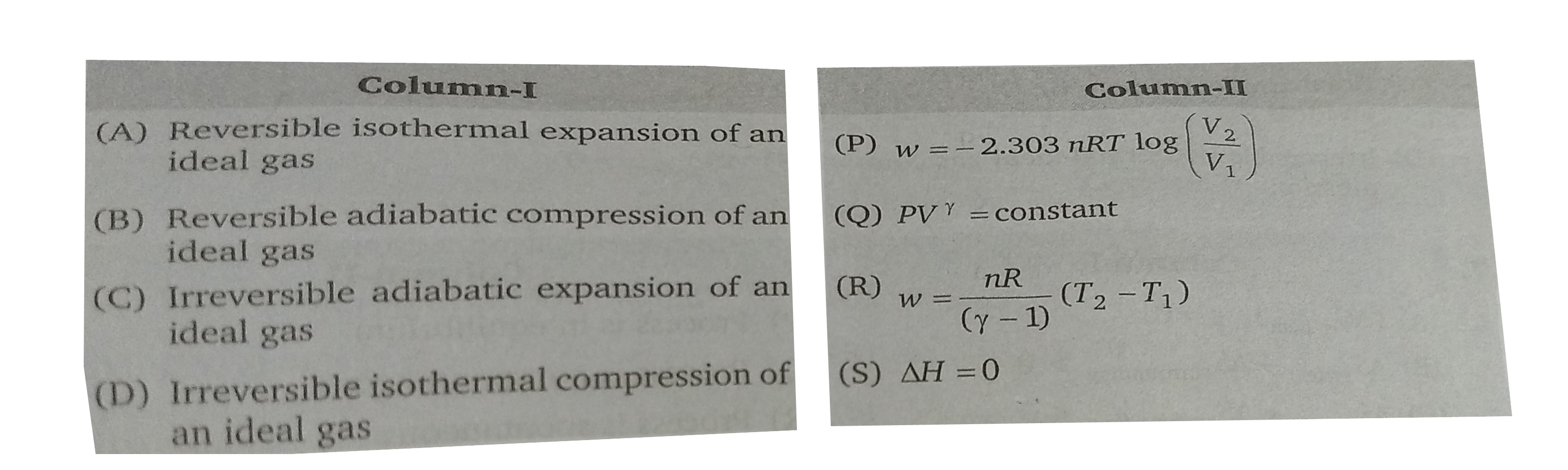
View SolutionMatch the following columns

View Solution
View Solution
View SolutionMatch the following columns

View SolutionMatch the following columns
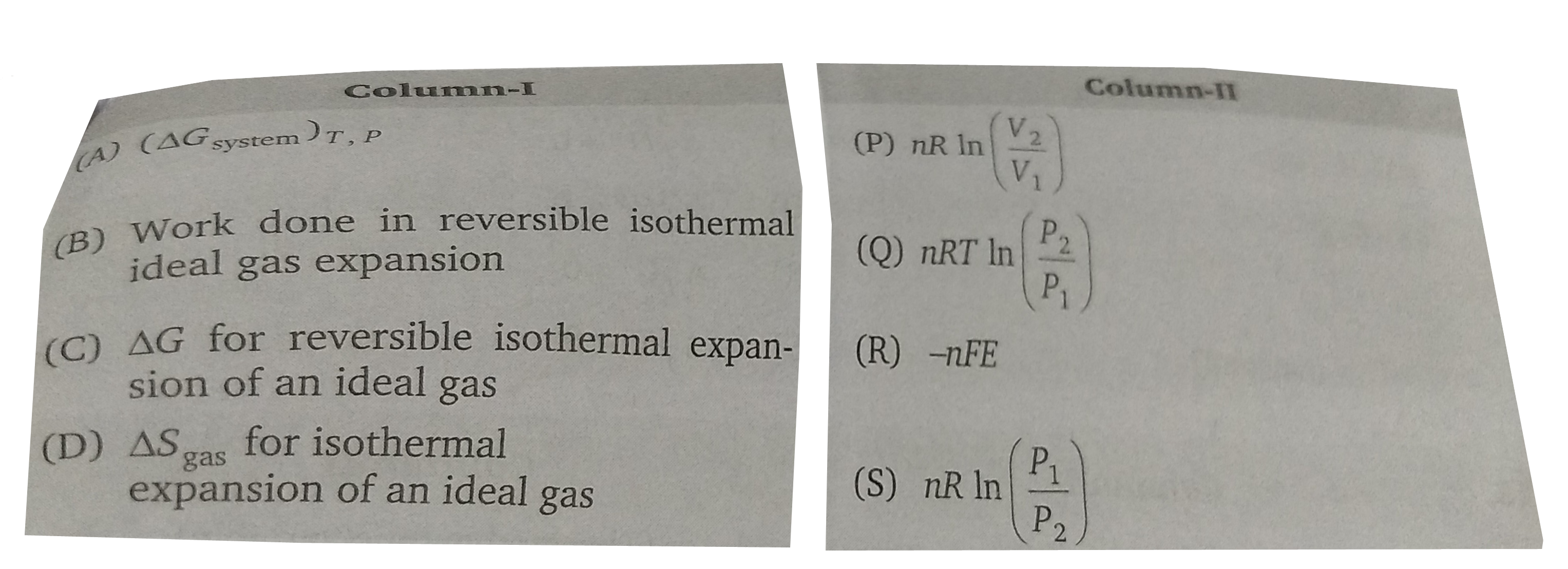
View SolutionMatch the following columns
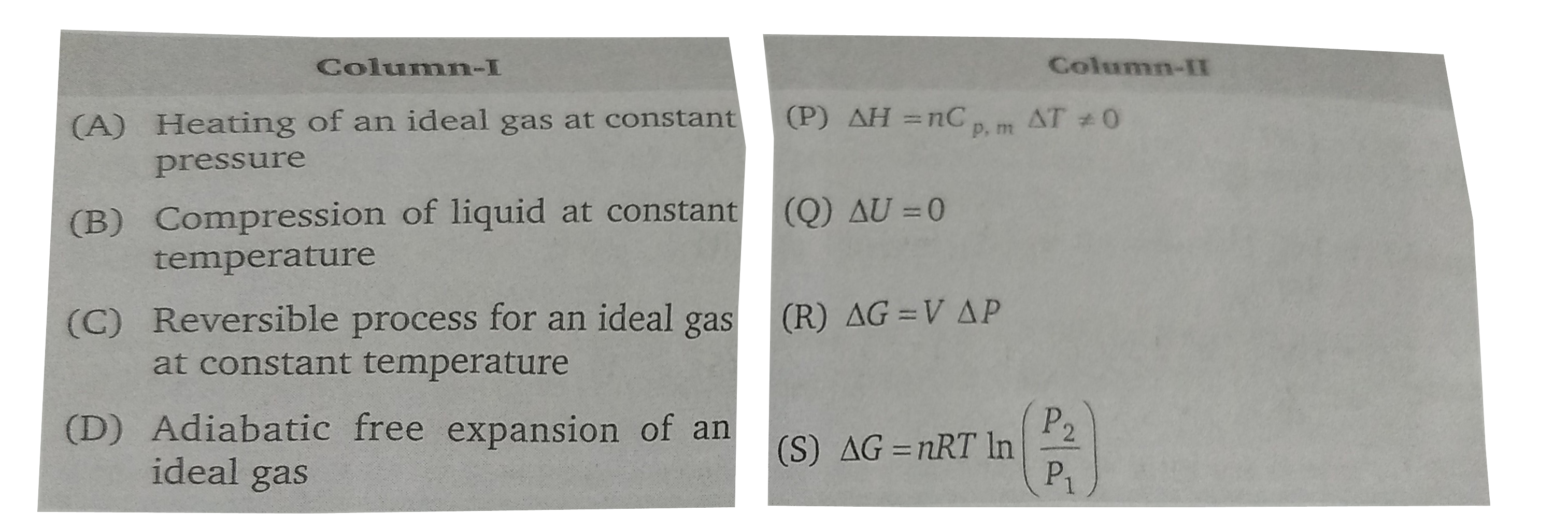
View SolutionMatch the following columns

View SolutionMatch the following columns

View Solution
View SolutionMatch the following columns

View SolutionMatch the following columns

View Solution
View SolutionStatement-I Heat and work are ''definite quantities''.
Statement-II Heat and work are not properties of a system. Their values depend on the path of the process and vary accordingly.
View SolutionThere is no change in internal energy for an ideal gas at constant temperature.
Internal energy of an ideal gas is a function of temperature only.
View SolutionAssertion: The heat absorbed during the isothermal expansion of an ideal gas against vacuum is zero.
Reason: The volume occupied by the molecules of an ideal gas is zero.
View Solution`DeltaH` and `DeltaU` are the same of the reaction, `N_(2)(g)+O_(2)(g)iff2NO(g)`,
All reactants and products are gases where all gases are ideal.
View SolutionStaetement -1: The magniyude of the work involed in an isothermal expansion is greater than that involved in an adiabatic expansion.
Statement -2: P-v cure (pon y -axas and V on X-axas) decrease more repidly for reversible asiabatic expansion compared to reversible isothermal expansion starting from same initial state.
View SolutionStatement -1: Entropy change in reversible adiabatic expansion of an ideal gas is zero.
Statement-2: The increase in entropy due to volume increase just compensates the decrease in entropy due to fall in temperature.
View SolutionThere cannot be chemical equilibrium in an open system.
There is no fixed mass in an open system.
View SolutionStatement -1: The Standard free energy changes of all spontaneously occurring reactions are negative .
Statement-2: The standard free energies of the elements in their standard states at 1 bar and 2985K aare taken aszero.
View SolutionStatement -1: Enthalpy and entropy of any elements substance in the standard states are taken as zero .
Statement-2: At absolute zero , particles of the perfectly crystalline substance become completely motionless.
(a)If both the statements are TRUE and STATEMENT-2 is the correct explanation of STATEMENT-9
(b)If both the statements are TRUE but STATEMENT-2 is NOT the correct explanation of STATEMENT-9
(c)If STATEMENT-1 is TRUE and STATEMENT-2 is FALSE
(d)If STATEMENT-1 is FALSE and STATEMENT-2 is TRUE
View SolutionStatement-1: A reaction which is spontaneous and accompained by decrease of randomness must be exothermic.
Statement -2: All exothermic reaction that are accomained by decrease of randomness.
View SolutionAssertion (A): May endothermic reactions that are not spontaneous at room temperature become spontaneous at high temperature.
Reason (R ) : Entropy of the system increases with increase in temperature.
View SolutionStatement-1: Decrease of free energy during the process under constant temperature and pressure provides a measure of its spontaneity.
Statement -2: A spontaneous change must have +ve sign of `DeltaS_("system").`
View SolutionStatment 1`|Delta_(f)H|" of "(H_(2)O,l)gt|Delta_(f)H|" of "(H_(2)O,g)`
Statment 2 `DeltaH_("condensation")` is negative.
(a)If both the statements are TRUE and STATEMENT-2 is the correct explanation of STATEMENT-1
(b)If both the statements are TRUE but STATEMENT-2 is NOT the correct explanation of STATEMENT-1
(c)If STATEMENT-1 is TRUE and STATEMENT-2 is FALSE
(d)If STATEMENT-1 is FALSE and STATEMENT-2 is TRUE
View SolutionAll combustion reactions are exothermic.
Enthalpies of products are greater than enthalpies of reactants `(Sigmav_(p)Delta_(f)H(P)gtSigmav_(R)Delta_(f)H(R))`
View SolutionEnthalpy of neutralization of `CH_(3)COOH` by NaOH is less than that of HCl by NaOH.
Enthalpy of neutralization of `CH_(3)COOH` is less because of the absorption of heat in the ionization process.
View SolutionAssertion`:-`Internal energy of a real gas may change during expansion at const. temperature.
Reason`:-` Internal energy of a real gas ia function of `T` & `P`.
View SolutionWork is a state function which is expressed in joule.
work appears only at the boundary of the system.
View SolutionThe expansion of a gas into an evacuated space takes place non-spontaneously.
A process in which all steps cannot be retraced by themselves is called a spontaneous process.
View SolutionA perfect gas undergoes a reversible adiabatic expansion from (300 K, 200 atm) to (90 K, 10 atm). Find the atomicity of gas.
View Solution5 mole of an ideal gas at temp. T are compressed isothermally from 12 atm. To 24 atm. Calculate the value of 10 r. Where, `r=("Work done along reversible process")/("Work done along single step irreversible process")" (Given : ln 2 = 0.7)"`
View SolutionA diatomic ideal gas is expanded according to `PV^(3)` = constant, under very high temperature (Assume vibration mode active). Calculate the molar heat capacity of gas (in cal / mol K) in this process.
View SolutionA heat engine is operating between 500 K to 300 K and it absorbs 10 kcal of heat from 500 K reservoir reversibly per cycle. Calculate the work done (in kcal) per cycle.
View SolutionMolar heat capacities at constant pressure for A, B and C are 3, 1.5 and 2 J/K mol. The enthalpy of reaction and entropy of reaction, A +2 B `rarr` 3C are 20 kJ/mol and 20 J/K mol at 300 K. Calculate `DeltaG` (in kJ / mol) for the reaction,
`(1)/(2)A+Brarr(3)/(2)C`
View SolutionStandard molar enthalpy of combustion of glucose is -2880 kJ. If only 25% of energy is available for muscular work and 1.0 km walk consumes 90 kJ of energy, what maximum distance (in km) a person can walk after eating 90 g of glucose.
View SolutionGiven `C_(2)H_(2)(g)+H_(2)(g)rarrC_(2)H_(4)(g): DeltaH^(@)=-175 " kJ mol"^(-1)`
`DeltaH_(f(C_(2)H_(4),g))^(@)=50 " kJ mol"^(-1), DeltaH_(f(H_(2)O,l))^(@)=-280 " kJ mol"^(-1), DeltaH_(f(CO_(2)g))^(@)=-390 " kJ mol"^(-1)`
If `DeltaH^(@)` is enthalpy of combustion (in kJ `"mol"^(-1)`) of `C_(2)H_(2)`(g), then calculate the value of `|(DeltaH^(@))/(257)|`
View SolutionThe integral enthalpies of solution of anhydrous `CuSO_(4)` (s) and hydrated `CuSO_(4).5H_(2)O(s)` are -70 kJ per mol and 10 kJ per mol respectively. Determine the magnitude of enthalpy of hydration of 0.1 mole anhydrous `CuSO_(4)` (s) as
`CuSO_(4)(s)+5H_(2)O(l)rarrCuSO_(4).5H_(2)O(s)`
View SolutionIf enthalpy of neutralisation of HCl by NaOH is -57 kJ `" mol"^(-1)` and with `NH_(4)OH` is -50 kJ `" mol"^(-1)`. Calculate enthalpy of ionisation of `NH_(4)OH` (aq).
View SolutionLattice energy of NaCl(s) is -790 kJ `" mol"^(-1)` and enthalpy of hydration is -785 kJ `" mol"^(-1)`. Calculate enthalpy of solution of NaCl(s).
View Solutionx g sample of `NH_(4)NO_(3)` is decomposed in a Bomb calorimeter. The temperature of calorimeter increase by `4^(@)C`. The heat capacity of the system is `1.25 " kJ"//.^(@)C`. Calculate the value of x. Given molar heat of decomposition of `NH_(4)NO_(3)` at constant volume is 400 kJ `" mol"^(-1)`.
View SolutionA heat engine operating between `227^(@)C` and `77^(@)C` absorbs 10 kcal of heat from the `227^(@)C` reservoir reversibly per cycle. Calculate total work done (in kcal) in two cycles.
View SolutionCalculate work done in chemical reaction (in kcal)
`A(s)+3B(g)rarrC(l)` at `227^(@)C` at 1 atm in closed vessel.
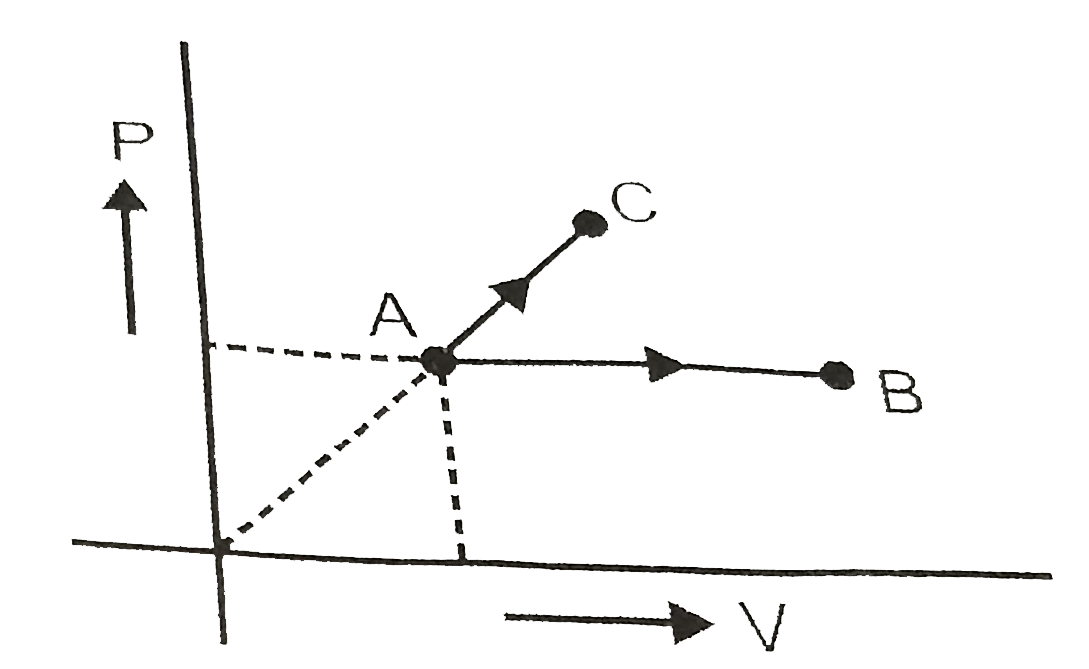
View SolutionOne mole ideal monoatomic gas is heated according to path AB and AC.
If temperature of state B and state C are equal.
Calculate `(q_(AC))/(q_(AB))xx10`.
View Solution
Level 3 questions and complete solutions for chapter THERMODYNAMICS of NARENDER AVASTHI CHEMISTRY (ENGLISH) of Class 11