Complete Solutions to EXERCISE 9.1 of chapter DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITY of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITY |
| TAMILNADU GOVT | EXERCISE 9.1 |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
Complete the table using calculator and use the result to estimate the limit.
`lim_(x rarr 2)(x-2)/(x^(2) - x - 2)`
 View Solution
View SolutionComplete the table using calculator and use the result to estimate the limit.
`lim_(x rarr 2)(x-2)/(x^(2) - 4)`
 View Solution
View SolutionComplete the table using calculator and use the result to estimate the limit.
`lim_(x rarr 0)((sqrt(x) + 3)-sqrt(3))/(x)`
 View Solution
View SolutionComplete the table using calculator and use the result to estimate the limit.
`lim_(x rarr -3)(sqrt(1-x) - 2)/(x+3)`
 View Solution
View SolutionComplete the table using calculator and use the result to estimate the limit.
`lim_(x rarr 0) (sin x)/(x)`
 View Solution
View SolutionUse the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x rarr 3)(4-x)`
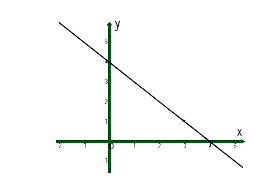 View Solution
View SolutionUse the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x rarr 1)(x^(2) + 2)`.
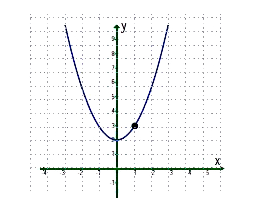 View Solution
View SolutionUse the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x rarr 2) f(x)` where `f(x) = {{:(4-x",",x ne 2),(0",", x = 2):}`
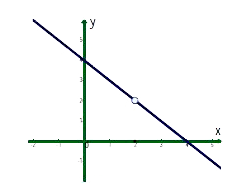 View Solution
View SolutionUse the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x rarr 1)f(x)` where `f(x) = {{:(x^(2)+2",",x ne 1),(1",", x = 1):}`
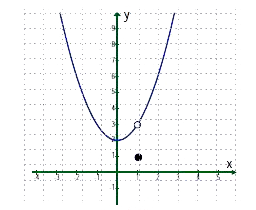 View Solution
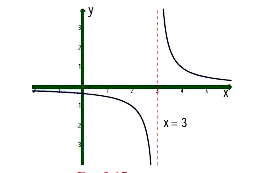
View SolutionUse the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x rarr 3)(1)/(x-3)`
 View Solution
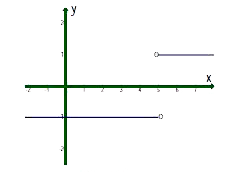
View SolutionUse the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x rarr 5)(|x-5|)/(x-5)`
 View Solution
View SolutionUse the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x rarr 0) sec x`
 View Solution
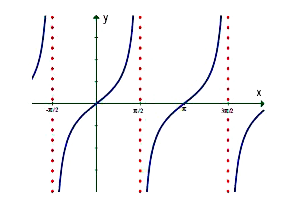
View SolutionUse the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x rarr (pi)/(2)) tan x`
 View Solution
View SolutionSketch the graph of f, then identify the values of `x_(0)` for which`lim_(x rarr x_(0)) f(x)` exists
`f(x) = {{:(x^(2)",",x lt 2),(8-2x",",2 lt x lt 4),(4",",x ge 4):}`View SolutionSketch the graph of f, then identify the values of `x_(0)` for which `lim_(x rarr x_(0)) f(x)` exists
`f(x) = {{:(sin x",",x lt 0),(1- cos x",",0 le x le pi),(cos x",",x gt pi):}`View SolutionWrite a brief description of the meaning of the notation `lim_(x rarr 8) f(x) = 25`.
View SolutionIf f(2) = 4, can you conclude anything about the limit of f(x) as x approaches 2?
View SolutionIf the limit of f(x) as x approaches 2 is 4, can you conclude anything about f(2)? Explain reasoning
View SolutionEvaluate : `lim_(x rarr 3)(x^(2) - 9)/(x-3)` if it exists by finding `f(3^(-))` and `f(3^(+))`.
View SolutionVerify the existence of `lim_(x rarr 1)f(x)`, where `f(x) = {{:((|x-1|)/(x-1)", for ",x ne 1),(0", for ",x = 1):}`.
View Solution
EXERCISE 9.1 questions and complete solutions for chapter DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITY of FULL MARKS MATHEMATICS(TAMIL) of Class 11
