Complete Solutions to Illustrative Example of chapter LINEAR MOMENTUM & ITS CONSERVATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | LINEAR MOMENTUM & ITS CONSERVATION |
| PHYSICS GALAXY | Illustrative Example |
| Number Of Questions | 42 |
| Academic Year | 2023-24 |
Figure shows a rod of mass 10 kg of length 100cm with some masses tied to it at different position. Find the point on the rod at which if the rod is picked over a knife edge, it will be in equilibrium about that knife edge.

View SolutionTwo children `A` and `B` of same mass (including their caps) `M` are sitting On a see-saw as shown in Fig. Initially, the beam is horizontal. At once, child `B` throws away his cap (mass `M/25`) which falls at point `Q`, midpoint of the left half of the beam, due to this the balance of beam is disturbed. To balance it again what is the mass in required to be put at point `P` on the right half of the beam?

View SolutionFigure shows a fixed wedge on which two blocks of masses `2 kg` and `3 kg` are placed on its smooth inclined surfaces. When the two blocks are released from rest, find the acceleration of centre of mass of the two blocks.

View SolutionFigure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is `R//2`. Find the centre of mass of the remaining part of the disc.

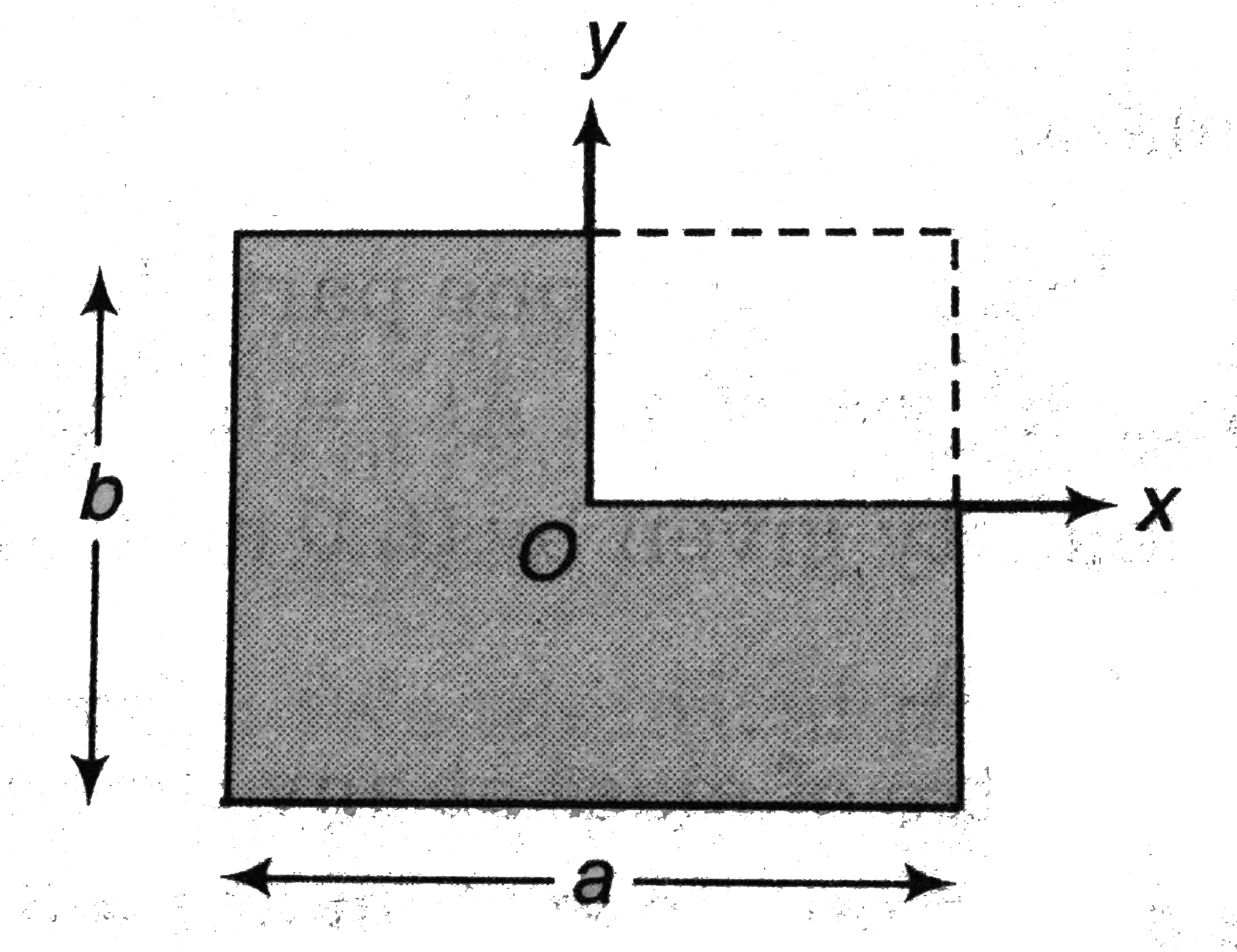
View SolutionConsider a rectangular plate of dimensions `axxb`. If this plate is considered to be made up of four rectangles of dimensions `a/2xxb/2` and we now remove one out of four rectangles. Find the position where the centre of mass of the remaining system will lie?
View SolutionThere are two masses `m_(1)` and `m_(2)`, placed at a distance `l` apart, let the centre of mass of this system is at a point named `C`. If `m_(1)` is displaced by `l_(1)` towards `C` and `m_(2)` is displaced by `l_(2)` away from `C`, find the distance from (C) where the new centre of mass will be located.
View SolutionLet there are three equal masses situated at the vertices of an equilateral triangle, as shown in Fig. Now particle `A` starts with a velocity `v_(1)` towards line `AB`, particle `B` starts with the velocity `v_(2)`, towards line `BC` and particle `C` starts with velocity `v_(3)` towards line `CA`. Find the displacement of the centre of mass of the three particles `A, B` and `C` after time `t`. What would it be if `v_(1)=v_(2)=v_(3)`?
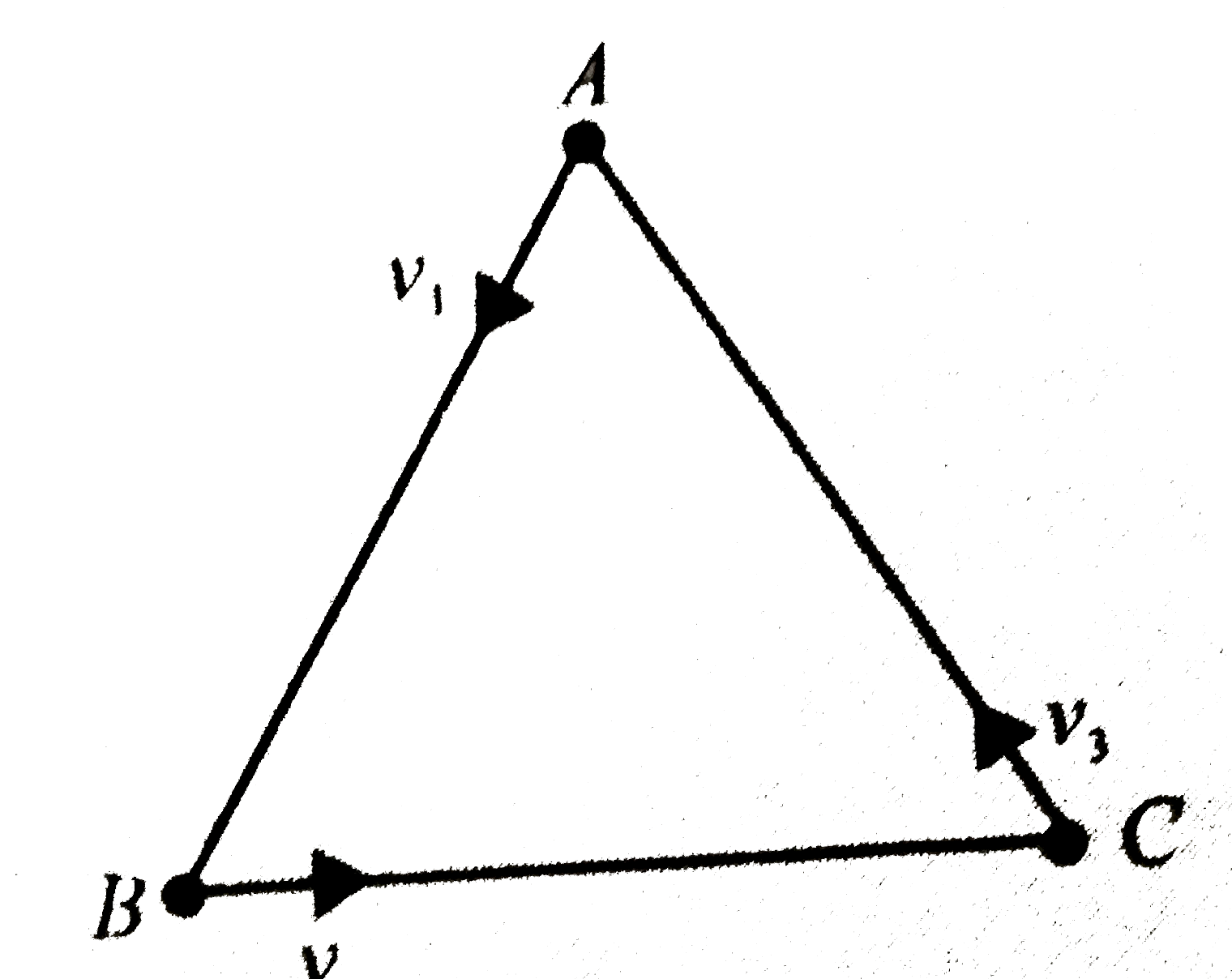
View SolutionAB is a uniformly shaped rod of length L and cross sectional are S, but its density varies with distance from one end A of the rod as `rho=px^(2)+c`, where p and c are positive constants. Find out the distance of the centre of mass of this rod from the end A.
View SolutionFind out the centre of mass of an isosceles triangle of base length a and alititude b. Assume that the mass of the triangle is uniformly distributed over its area.
View SolutionFind out the centre of mass of a composite object shown in figure-4.28. Object consists of a cone with its base joint with the base of a hemisphere. The dimensions of the object are shown in figure. Assume uniform density of the system, find the centre of mass of this system.

View SolutionA table has a heavy circular top of radius 1 m and mass 20 kg. It has four light legs of lengths 1 m fixed symmetrically on its circumference. (a) What is the maximum mass that may be placed any where on this table without toppling the table ? (b) What is the area of the table tope over which any weight may be placed without toppling it ?
View SolutionFind moment of inertia of half disc of radius `R_2` and mass `M` about its centre. A smaller half disc of radius `R_1` is cut from this disc

View SolutionFrom a solid sphere a small part A is cut by a plane at a distance `R//2` from the centre as shown in figure-4.32. Find the centre of mass of object A.

View SolutionA plank of mass M and length L is at rest on a frictionless floor. At one end of it a child of mass m is standing as shown in figure-4.41. If child walks towards the other end, find the distance, which the plank moves (a) till the child reaches the centre of the plank, (b) till the child reaches the other end of the plank.
View SolutionFigure shows a flat car of mass `M` on a frictionless road. A small massless wedge is fitted on it as shown. A small ball of mass `m` is released from the top of the wedge, it slides over it and falls in the hole at distance `l` from the initial position of the ball. Find the distance the flat car moves till the ball gets into the hole.

View SolutionA man of mass M jumps from an aeroplane as shown in figure-4.43. He sees the hard ground below him and a lake at a distance d from the point directly below him. He immediately put off his jacket (mass=m) and throws it in a direction directly away from the lake. If he just fail to strike the ground, find distance he should walk know to pick his jacket. (Neglect air resistance and take the velocity of man at the time of jump with respect to earth is zero.)

View SolutionTwo men of same mass m hold the two ends of a rope and start pulling each other on a friction less plane. Find the position where they will meet. Is there any difference, if masses of men are not equal.
View SolutionA flat car of mass `m` is at rest on a frictionless floor with a child of mass `m` standing at its edge. If the child jumps off from the car towards right with an initial velocity `u`, with respect to the car, find the velocity of the car after its jump.
View SolutionA flat car of mass `M` with a child of mass `m` is moving with a velocity `v_(1)`. The child jumps in the direction of motion of car with a velocity `u` with respect to the car. Find the final velocities of the child and that of the car after jump.
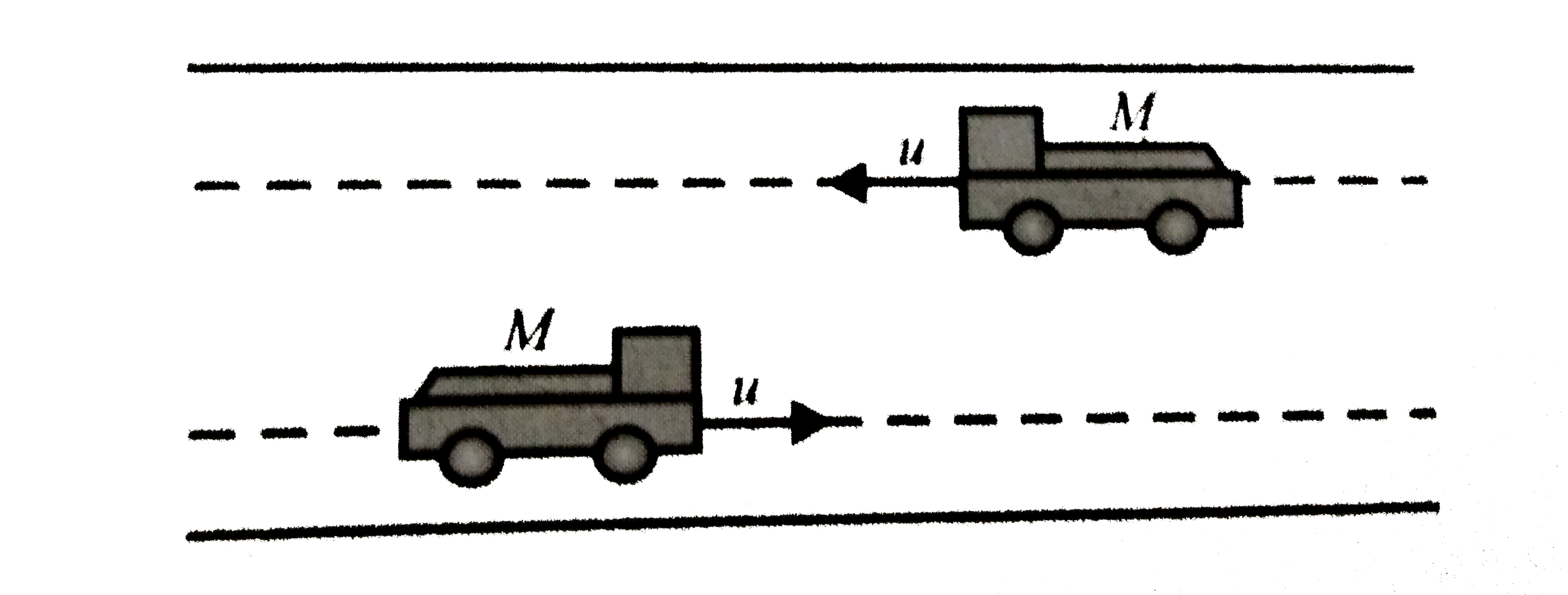
View SolutionTwo trucks of mass `M` each are moving in opposite direction on adjacent parallel tracks with same velocity `u`. One is carrying potatoes and other is carrying onions, a bag of potatoes has a mass `m_(1)` and a bag of onions has a mass `m_(2)` (included i the mass of truck `M`). When trucks get close to each other while passing the drivers exchange a bag with the other one by throwing the other one. Find the final velocities of the trucks after exchange of the bags.
View SolutionFigure shows two blocks of masses `5 kg` and `2 kg` placed on a frictionless surface and connected with a spring. An external kick gives a velocity of `14 m//s` to the heavier block in the direction of lighter one. Deduce (a) velocity gained by the centre of mass and (b) the separate velocities of the two blocks in the centre of mass coordinates just after the kick.

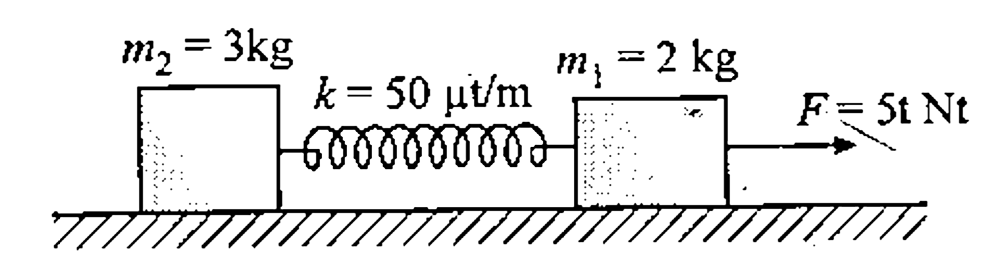
View SolutionTwo bars of masses `m_1` and `m_2` connected by a weightless spring of stiffness `ϰ` (figure) rest on a smooth horizontal plane.

Bar 2 is shifted a small distance `x` to the left and then released. Find the velocity of the centre of inertia of the system after bar 1 breaks off the wall.
View SolutionA block of mass `m` is connected to another block of mass `M` by a massless spring of spring constant `k`. the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force `F` starts acting on the block of mass `M` of pull it. Find the maximum extension of the spring

View SolutionA shell is fixed from a cannon with a speed of `100 m//s` at an angle `60^(@)` with the horizontal (positive x-direction). At the highest point of its trajectory, the shell explodes into two equal fragments. One of the fragments moves along the negative x-direction with a speed of `50 m//s`. What is the speed of the other fragment at the time of explosion.
View SolutionA shell is fired from a cannon with a speed of `100 m//s` at an angle `30^(@)`with the vertical (`y`-direction). At the highest point of its trajectory, the shell explodes into two fragments of masses in the ratio `1:2`. The lighter fragment moves vertically upwards with an initial speed of `200 m//s`. What is the speed of the heavier fragment at the time of explosion?
View SolutionA body of mass 10 kg is pulled with a time varying horizontal force `F=2t^(2)` N on a rough surface having friction coefficient `mu=0.2`. Find the speed of block after 6 seconds.
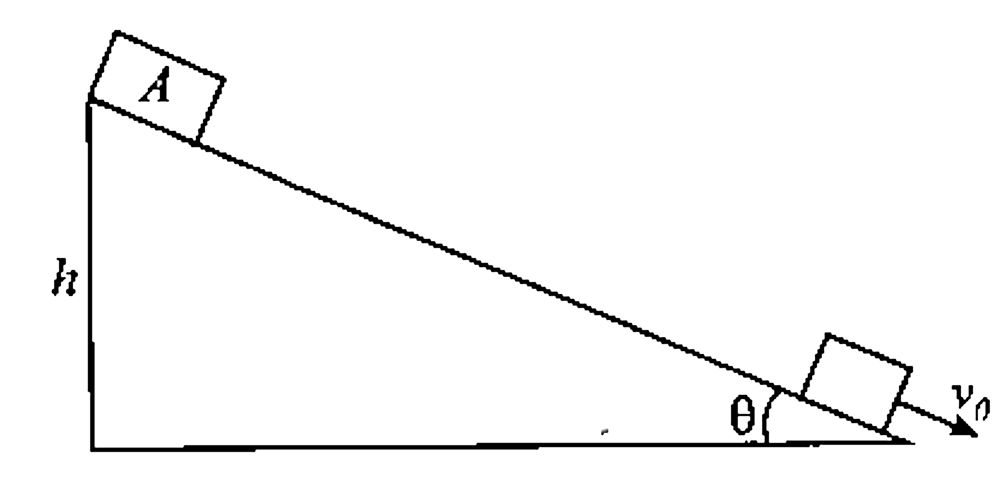
View SolutionA block of A is released from rest from the top of wedge block of height h shown in figure-4.55. If velocity of block when it reaches the bottom of inclive is `v_(0)`, find the time os sliding.
View SolutionOn a spring block system shown in figure-4.56, a time varying force F=5t N is applied on 2 kg mass. After 10 s, velocity of 3 kg mass is `30 m//sec`. Find velocity of 2 kg mass at this instant.
View SolutionA tank-car of mass M is at rest on a road. At t=0, a force F starts acting on the tank-car also the rain fall starts, in vertical direction, as shown in figure-4.57. The rain is falling with a velocity `v_(r)` with respect to earth and the rate of collection of water in the tank is `r kg//s`. find the velocity of the tank-car as a function of time t.
View SolutionA cart loaded with sand moves along a horizontal floor due to a constant force `F` coinciding in direction with cart's velocity vector. In the process, the sand spills through a hole in the bottom with a constant rate `mukg//s.` Find the acceleration and velocity of the cart at the moment `t`, if at the initial moment `t=0` the cart with loaded sand had mass `m_(0)` and its velocity was equal to zero. Friction is to be neglected.
View SolutionA beam of gas molecules is incident normally on a plate AB. Each gas molecule has mass m and velocity V. The incident beam falls on an area A on the plate and all the molecule strike the plate elastically. Number of molecules in unit volume of the beam is n. When the plate is moved to right (see fig.) a force `F_(1)` is needed to keep it moving with constant velocity u `(gt V)` . When the plate is moved to left with constant velocity u, an external force `F_(2)` is needed. Find `F_(2) – F_(1)`.

View SolutionA ball is dropped on a floor from a height `h`. If the coefficient of restitution is `e`, find the height to which the ball will rise after touching the floor and the time it will take to come to rest again.
View SolutionAn elevator platform is going up at a speed of `20 m//s` and during its upward motion a small ball of `50 g` mass, falling in downward direction, strikes the platform at speed `5 m//s`. Find the speed with which the ball rebounds.
View SolutionA neutron moving at a speed v undergoes a head-on elastic collision with a nucleus of mass number A at rest. The ratio of the kinetic energies of the neutron after and before collision is :
View SolutionTwo balls marked 1 and 2 of the same mass m and a third ball marked 3 of mass M are arranged over a smooth horizontal surface as shown in the figure. Ball 1 moves with a velocity `v_(1)` towards ball 2. All collisions are assumed to be elastic. If `Mltm`, the number of collisions between the balls will be.

View SolutionTwo balls approaching each other along two perpendicular directions and collide at the intersection. After the collision, they stick together. If one ball has a mass of 14.5 kg and an initial speed of `11.5 m//s` and the other has a mass of 17.5 kg and an initial speed of `15.5 m//s`, what will be their speed and direction immediately after impact ?
View SolutionA ball of a mass m hits the floor with as speed v making an angle of incidence `theta` with the normal. The coefficient of restitution is e. Find the speed of the reflected ball and the angle of reflection of the ball.
 `
`
View SolutionA wedge mass `m` rest on horizontal surface. The inclination of the wedge is `alpha`. A ball of mass `m` moving horizontal with speed `u` hits the inclined face of the wedge inelastically and after hitting slides up the inclined face of the wedge. Find the velocity of the wedge just after collision. Neglect any friction.
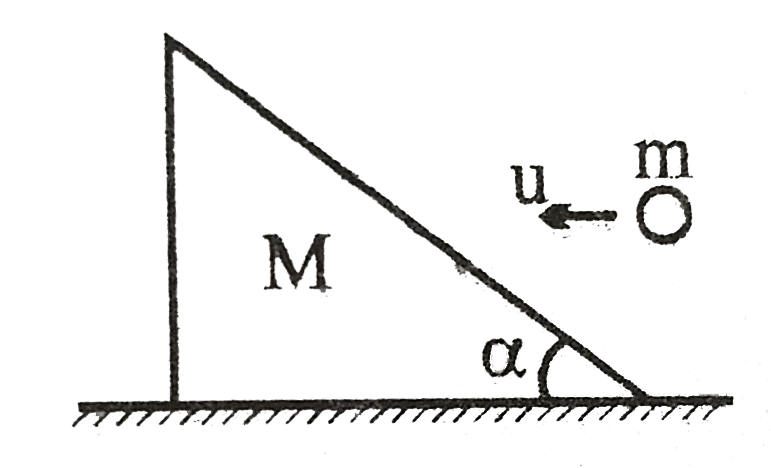
View SolutionA ball of mass m is just disturbed from the top of a fixed smooth circular tube in a vertical plane and falls impinging on a ball of mass 2 m at the bottoom. The coefficient of restituion is `1//2`. Find the heights to which the balls rise after a second impact.
View SolutionA mass M=1 kg lies on a smooth horizontal base of a rough inclined plane at an angle `37^(@)` with the horizontal as shown in figure-4.81. A bullet of mass m=0.1 kg is fired horizontally with a velocity `u=110 m//s` and gets embeded in it almost immediately. The impluse imparted carries the combined mass up the incline and finally lands on the horizontal level with the horizontal base.
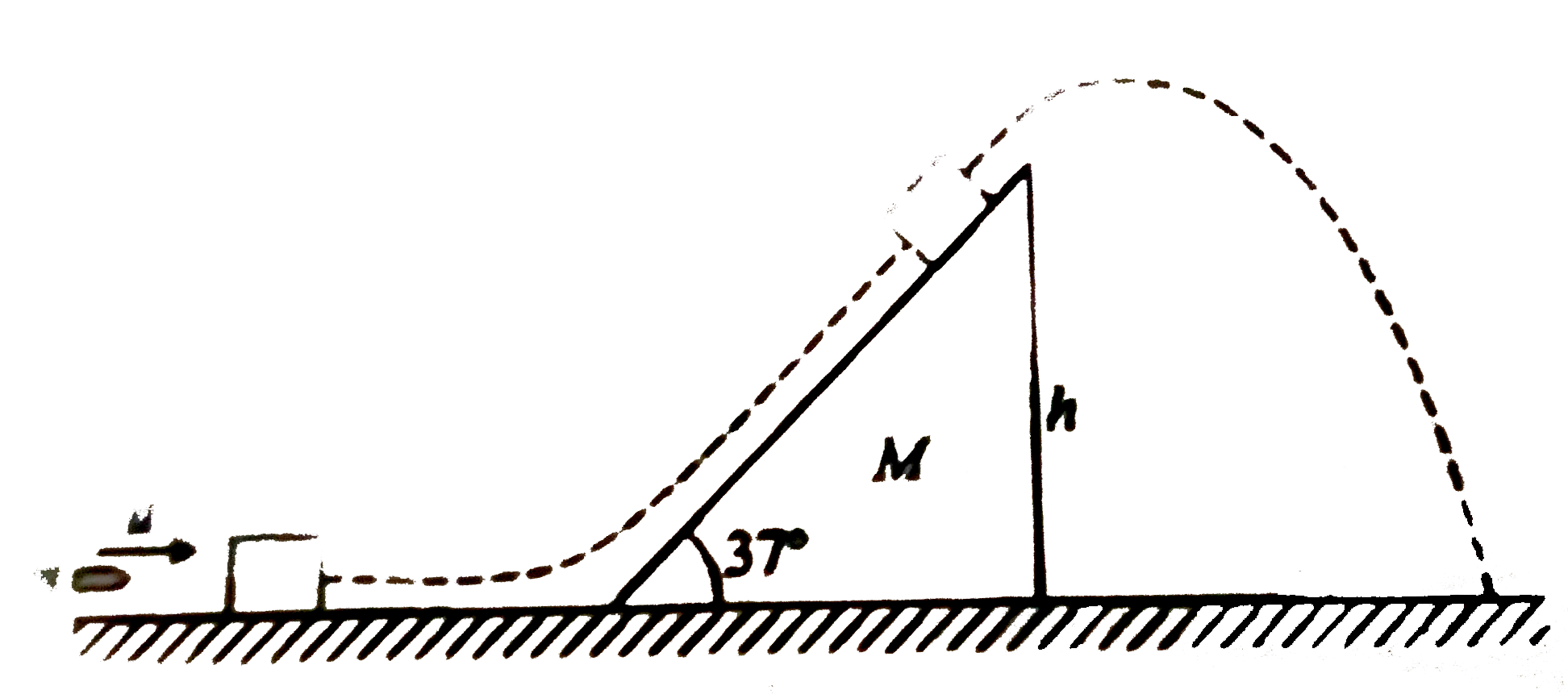
If the length of the incline is I=1.8 m and the incline offers a coefficient of kinetic friction 0.5 to the sliding of the mass, find the horizontal distance from the base of the incline to the point of landing of the combined mass. Assume the contact of the incline with the horizontal plane is smooth and mass is not jerked when starts up on incline plane.
View SolutionA bead can slide on a smooth straight wire and a particle of mass `m` attached to the bead by a light string of length `L`. The particle is held in contact with the wire and with the string taut and is then let fall. If the bead has mass `2m` then when the string makes an angle `theta` with the wire, the bead will have slipped a distance.

View SolutionFigure shows a block `A` of mass `6 m` having a smooth semicircular groove of radius a placed on a smooth horizontal surface. A block `B` of mass `m` is released from a position in groove where its radius is horizontal. Find the speed of the bigger block when the smaller block reaches its bottom most position.
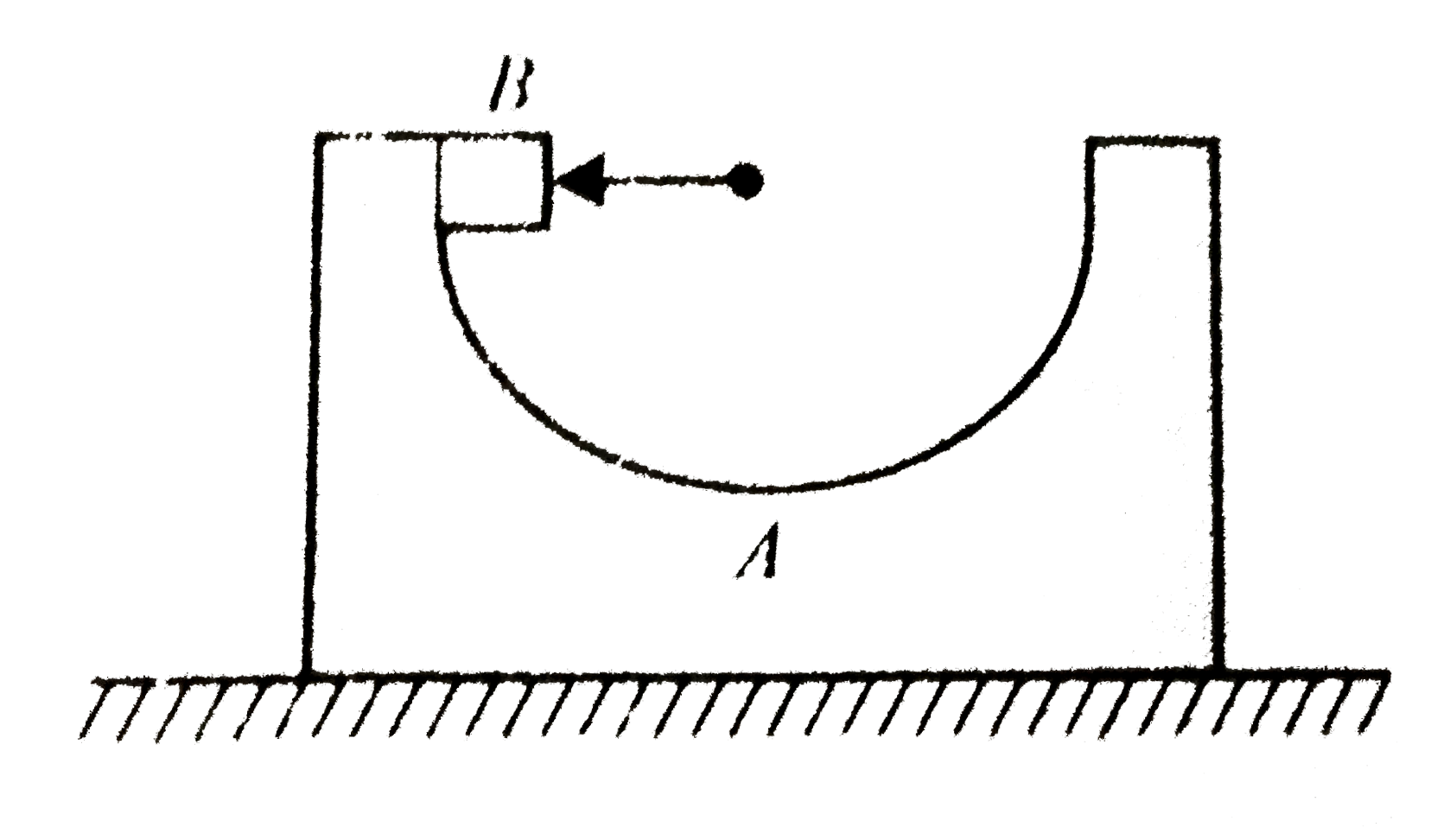
View Solution
Illustrative Example questions and complete solutions for chapter LINEAR MOMENTUM & ITS CONSERVATION of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 11